7.2.3 三角函数的诱导公式 课件(共67张PPT)2023-2024学年高中数学苏教版必修第一册
文档属性
| 名称 | 7.2.3 三角函数的诱导公式 课件(共67张PPT)2023-2024学年高中数学苏教版必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:58:13 | ||
图片预览







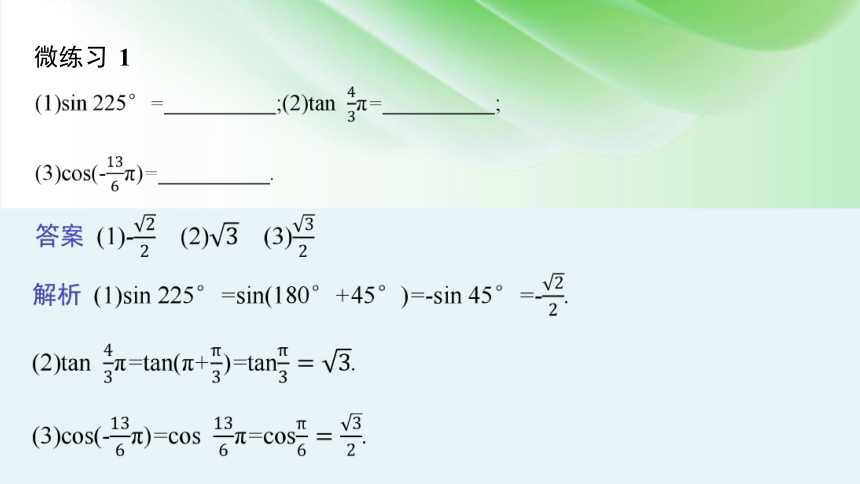
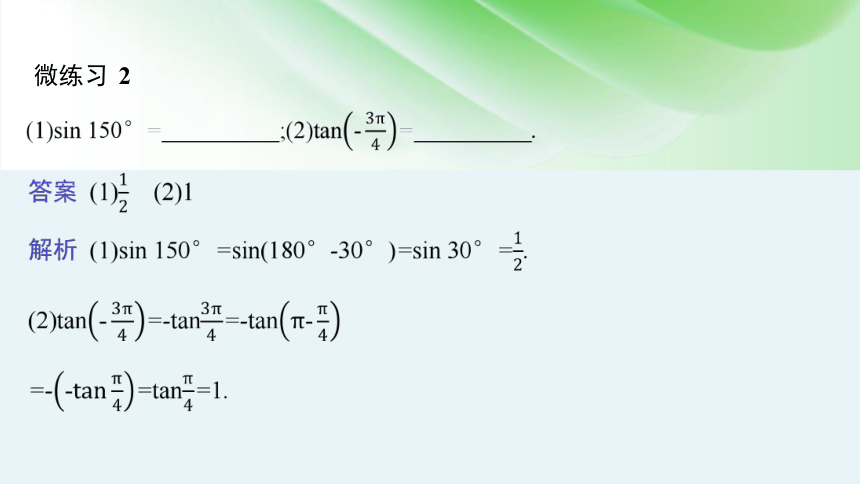

文档简介
(共67张PPT)
高中数学苏教版必修第一册
第7章 三角函数
7.2 三角函数的概念
7.2.3 三角函数的诱导公式
第1课时 诱导公式一、二、三、四
课标阐释 思维脉络
1.借助单位圆的对称性,利用定义推导出诱导公式(α±π的正弦、余弦、正切),并熟练掌握.(数学抽象)
2.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.(数学运算、逻辑推理)
情境导入
南京眼和辽宁的生命之环均利用完美的对称展现自己的和谐之美.而三角函数与(单位)圆是紧密联系的,它的基本性质是圆的几何性质的代数表示,例如,同角三角函数的基本关系表明了圆中的某些线段之间的关系.圆有很好的对称性:以圆心为对称中心的中心对称图形;以任意直径所在直线为对称轴的轴对称图形.
你能利用这种对称性并借助单位圆,
讨论任意角α的终边与π±α,-α的对称
关系吗 sin(π+α)、sin(π-α)、sin(-α)与
sin α又有怎样的关系呢
知识点拨
诱导公式一、二、三、四
1.诱导公式一
终边相同的角的同一三角函数值相等.
sin(α+2kπ)= sin α (k∈Z),cos(α+2kπ)= cos α (k∈Z),tan(α+2kπ)= tan α (k∈Z).
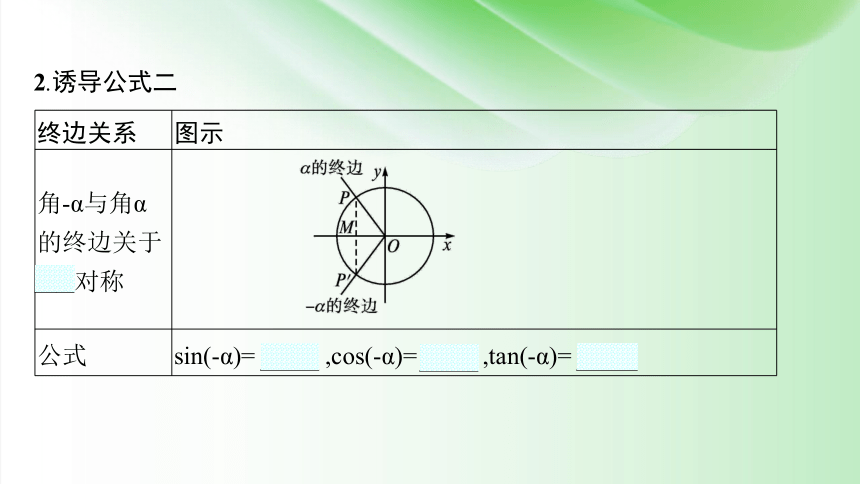
2.诱导公式二
终边关系 图示
角-α与角α的终边关于x轴对称
公式 sin(-α)= -sin α ,cos(-α)= cos α ,tan(-α)= -tan α
微思考
诱导公式一~四各自的作用是什么
提示
诱导公式 作用
公式一 将角转化为0~2π求值
公式二 将0~2π内的角转化为0~π之间的角求值
公式三 将负角转化为正角求值
公式四 将角转化为0~求值
微判断
(1)诱导公式中角α是任意角.( )
(3)sin(180°-200°)=-sin 200°.( )
(4)若α,β满足α+β=π,则sin α=sin β.( )
答案 (1)× (2)√ (3)× (4)√
3.诱导公式三
终边关系 图示
角π-α与角α的终边关于y轴对称
公式 sin(π-α)= sin α ,cos(π-α)= -cos α ,tan(π-α)= -tan α
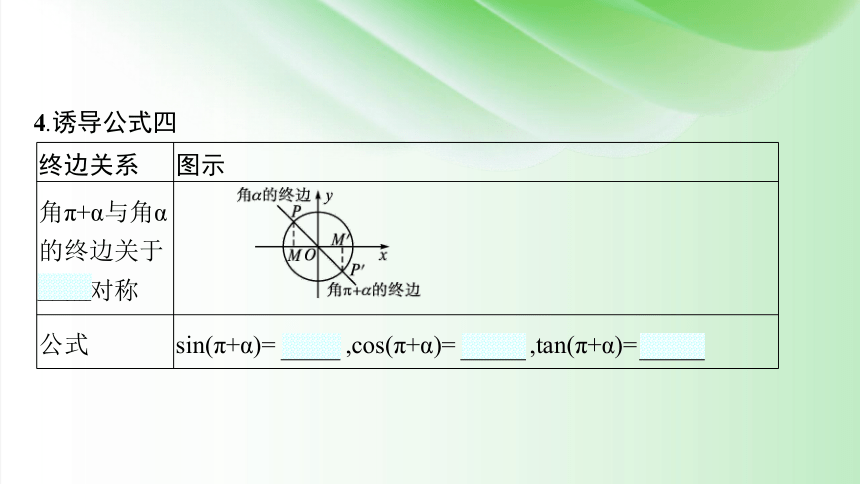
4.诱导公式四
终边关系 图示
角π+α与角α的终边关于原点对称
公式 sin(π+α)= -sin α ,cos(π+α)= -cos α ,tan(π+α)= tan α
微练习 1
微练习 2
微技巧
“函数名不变,符号看象限”.
“函数名不变”是指等式两边的三角函数同名;
“符号看象限”是指把原角看成锐角时新角在原函数下的符号,由新角所在象限确定符号.如sin(π+α),若把α看成锐角,则π+α在第三象限,所以取负值,故sin(π+α)=-sin α.
探究一
利用诱导公式求三角函数值
例1(1)sin 750°= ,cos(-2 040°)= ;
反思感悟利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用公式一或三来转化.
(2)“大化小”:用公式一将角化为0°到360°间的角.
(3)“小化锐”:用公式二或四将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.
变式训练1求下列各三角函数式的值:
(1)sin 1 320°;
(3)tan(-945°).
(3)tan(-945°)=-tan 945°
=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)
=-tan 45°=-1.
探究二
利用诱导公式化简求值问题
例2化简下列各式:
反思感悟三角函数式化简的常用方法
(1)合理转化:①将角化成2kπ±α,π±α,k∈Z的形式.
②依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
变式训练2化简下列各式:
(2)sin(π+α)cos(-α)+sin(2π-α)cos(π-α)+sin αcos(π+α)tan(-π-α).
探究三
给值(或式)求值问题
延伸探究将本例3题中的“-”改为“+”,“+”改为“-”,其他不变,应如何解答
要点笔记解决给值求值问题的策略
(1)解决给值求值问题,首先要仔细观察条件式与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
素养形成
思想方法——分类讨论思想在诱导公式中的应用
分析因为n∈Z,所以n可能为偶数,也可能为奇数,两种情况下诱导公式所得结果不同,所以需要分类讨论.
当堂检测
1.计算cos(-600°)=( )
答案 D
解析 cos(-600°)=cos 600°=cos(360°+240°)=cos 240°
=cos(180°+60°)=-cos 60°=- .
答案 A
3.在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α= ,则sin β= .
4.已知600°角的终边上有一点P(a,-3),则a的值为 .
答案 ②③⑤
高中数学苏教版必修第一册
第7章 三角函数
7.2 三角函数的概念
7.2.3 三角函数的诱导公式
第2课时 诱导公式五、六
课标阐释 思维脉络
1.借助单位圆的对称性,利用定义推导出诱导公式( ±α的正弦、余弦、正切),并熟练掌握.(数学抽象)
2.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.(数学运算、逻辑推理)
情境导入
同学们听了老师的记忆口诀后,更是摸不着头脑,老师随后进行了解释,同学们茅塞顿开,都拍手叫好.
你知道老师是如何解释的这句口诀“奇变偶不变,符号看象限”吗 六组诱导公式左边的角还能统一写成什么形式
知识点拨
诱导公式五、六
名师点析 1.名称:诱导公式五、六, ±α的正弦(余弦)函数值,分别转化为α的余弦(正弦)函数值.
2.符号:函数值前面加上一个把α看成锐角时原函数值的符号.
3.作用:利用诱导公式五或六,可以实现正弦函数与余弦函数的相互转化.
4.简记:“函数名改变,符号看象限”.
微判断
(1)cos(α- )=cos α.( )
(2)若cos 10°=a,则sin 100°=a.( )
(3)若α为第二象限角,则sin(α- )=-cos α.( )
答案 (1)× (2)√ (3)√
微练习
微思考
你能推导出tan( +α)、tan( -α)与tan α之间的关系吗
探究一
利用诱导公式求值
反思感悟利用诱导公式化简三角函数式的步骤
利用诱导公式可把任意角的三角函数转化为锐角三角函数,即
口诀是“负化正,大化小,化到锐角再查表”.
探究二
利用诱导公式证明恒等式
例2求证:
反思感悟利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除差异.
探究三
诱导公式的综合应用
反思感悟用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行切化弦,以保证三角函数名最少.
(2)对于π±α和 ±α这两套诱导公式,切记运用前一套公式不变名,而运用后一套公式必须变名.
素养形成
诱导公式在三角形中的应用
分析首先利用诱导公式化简已知的两个等式,然后结合sin2A+cos2A=1,求出cos A的值,再利用A+B+C=π进行求解.
反思感悟在△ABC中,常用到以下结论:
sin(A+B)=sin(π-C)=sin C,
cos(A+B)=cos(π-C)=-cos C,
tan(A+B)=tan(π-C)=-tan C,
解 ∵A+B+C=π,
∴A+B-C=π-2C,A-B+C=π-2B.
又B,C为△ABC的内角,∴C=B,
故△ABC为等腰三角形.
当堂检测
答案 B
解析 cos(450°+θ)=cos(90°+θ)=-sin θ=- .
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
谢谢观看
高中数学苏教版必修第一册
第7章 三角函数
7.2 三角函数的概念
7.2.3 三角函数的诱导公式
第1课时 诱导公式一、二、三、四
课标阐释 思维脉络
1.借助单位圆的对称性,利用定义推导出诱导公式(α±π的正弦、余弦、正切),并熟练掌握.(数学抽象)
2.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.(数学运算、逻辑推理)
情境导入
南京眼和辽宁的生命之环均利用完美的对称展现自己的和谐之美.而三角函数与(单位)圆是紧密联系的,它的基本性质是圆的几何性质的代数表示,例如,同角三角函数的基本关系表明了圆中的某些线段之间的关系.圆有很好的对称性:以圆心为对称中心的中心对称图形;以任意直径所在直线为对称轴的轴对称图形.
你能利用这种对称性并借助单位圆,
讨论任意角α的终边与π±α,-α的对称
关系吗 sin(π+α)、sin(π-α)、sin(-α)与
sin α又有怎样的关系呢
知识点拨
诱导公式一、二、三、四
1.诱导公式一
终边相同的角的同一三角函数值相等.
sin(α+2kπ)= sin α (k∈Z),cos(α+2kπ)= cos α (k∈Z),tan(α+2kπ)= tan α (k∈Z).
2.诱导公式二
终边关系 图示
角-α与角α的终边关于x轴对称
公式 sin(-α)= -sin α ,cos(-α)= cos α ,tan(-α)= -tan α
微思考
诱导公式一~四各自的作用是什么
提示
诱导公式 作用
公式一 将角转化为0~2π求值
公式二 将0~2π内的角转化为0~π之间的角求值
公式三 将负角转化为正角求值
公式四 将角转化为0~求值
微判断
(1)诱导公式中角α是任意角.( )
(3)sin(180°-200°)=-sin 200°.( )
(4)若α,β满足α+β=π,则sin α=sin β.( )
答案 (1)× (2)√ (3)× (4)√
3.诱导公式三
终边关系 图示
角π-α与角α的终边关于y轴对称
公式 sin(π-α)= sin α ,cos(π-α)= -cos α ,tan(π-α)= -tan α
4.诱导公式四
终边关系 图示
角π+α与角α的终边关于原点对称
公式 sin(π+α)= -sin α ,cos(π+α)= -cos α ,tan(π+α)= tan α
微练习 1
微练习 2
微技巧
“函数名不变,符号看象限”.
“函数名不变”是指等式两边的三角函数同名;
“符号看象限”是指把原角看成锐角时新角在原函数下的符号,由新角所在象限确定符号.如sin(π+α),若把α看成锐角,则π+α在第三象限,所以取负值,故sin(π+α)=-sin α.
探究一
利用诱导公式求三角函数值
例1(1)sin 750°= ,cos(-2 040°)= ;
反思感悟利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用公式一或三来转化.
(2)“大化小”:用公式一将角化为0°到360°间的角.
(3)“小化锐”:用公式二或四将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.
变式训练1求下列各三角函数式的值:
(1)sin 1 320°;
(3)tan(-945°).
(3)tan(-945°)=-tan 945°
=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)
=-tan 45°=-1.
探究二
利用诱导公式化简求值问题
例2化简下列各式:
反思感悟三角函数式化简的常用方法
(1)合理转化:①将角化成2kπ±α,π±α,k∈Z的形式.
②依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
变式训练2化简下列各式:
(2)sin(π+α)cos(-α)+sin(2π-α)cos(π-α)+sin αcos(π+α)tan(-π-α).
探究三
给值(或式)求值问题
延伸探究将本例3题中的“-”改为“+”,“+”改为“-”,其他不变,应如何解答
要点笔记解决给值求值问题的策略
(1)解决给值求值问题,首先要仔细观察条件式与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
素养形成
思想方法——分类讨论思想在诱导公式中的应用
分析因为n∈Z,所以n可能为偶数,也可能为奇数,两种情况下诱导公式所得结果不同,所以需要分类讨论.
当堂检测
1.计算cos(-600°)=( )
答案 D
解析 cos(-600°)=cos 600°=cos(360°+240°)=cos 240°
=cos(180°+60°)=-cos 60°=- .
答案 A
3.在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α= ,则sin β= .
4.已知600°角的终边上有一点P(a,-3),则a的值为 .
答案 ②③⑤
高中数学苏教版必修第一册
第7章 三角函数
7.2 三角函数的概念
7.2.3 三角函数的诱导公式
第2课时 诱导公式五、六
课标阐释 思维脉络
1.借助单位圆的对称性,利用定义推导出诱导公式( ±α的正弦、余弦、正切),并熟练掌握.(数学抽象)
2.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.(数学运算、逻辑推理)
情境导入
同学们听了老师的记忆口诀后,更是摸不着头脑,老师随后进行了解释,同学们茅塞顿开,都拍手叫好.
你知道老师是如何解释的这句口诀“奇变偶不变,符号看象限”吗 六组诱导公式左边的角还能统一写成什么形式
知识点拨
诱导公式五、六
名师点析 1.名称:诱导公式五、六, ±α的正弦(余弦)函数值,分别转化为α的余弦(正弦)函数值.
2.符号:函数值前面加上一个把α看成锐角时原函数值的符号.
3.作用:利用诱导公式五或六,可以实现正弦函数与余弦函数的相互转化.
4.简记:“函数名改变,符号看象限”.
微判断
(1)cos(α- )=cos α.( )
(2)若cos 10°=a,则sin 100°=a.( )
(3)若α为第二象限角,则sin(α- )=-cos α.( )
答案 (1)× (2)√ (3)√
微练习
微思考
你能推导出tan( +α)、tan( -α)与tan α之间的关系吗
探究一
利用诱导公式求值
反思感悟利用诱导公式化简三角函数式的步骤
利用诱导公式可把任意角的三角函数转化为锐角三角函数,即
口诀是“负化正,大化小,化到锐角再查表”.
探究二
利用诱导公式证明恒等式
例2求证:
反思感悟利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除差异.
探究三
诱导公式的综合应用
反思感悟用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行切化弦,以保证三角函数名最少.
(2)对于π±α和 ±α这两套诱导公式,切记运用前一套公式不变名,而运用后一套公式必须变名.
素养形成
诱导公式在三角形中的应用
分析首先利用诱导公式化简已知的两个等式,然后结合sin2A+cos2A=1,求出cos A的值,再利用A+B+C=π进行求解.
反思感悟在△ABC中,常用到以下结论:
sin(A+B)=sin(π-C)=sin C,
cos(A+B)=cos(π-C)=-cos C,
tan(A+B)=tan(π-C)=-tan C,
解 ∵A+B+C=π,
∴A+B-C=π-2C,A-B+C=π-2B.
又B,C为△ABC的内角,∴C=B,
故△ABC为等腰三角形.
当堂检测
答案 B
解析 cos(450°+θ)=cos(90°+θ)=-sin θ=- .
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
谢谢观看
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
