9.2.1向量的加减法 课件(共63张PPT)2023-2024学年高中数学苏教版必修第二册
文档属性
| 名称 | 9.2.1向量的加减法 课件(共63张PPT)2023-2024学年高中数学苏教版必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:56:40 | ||
图片预览










文档简介
(共63张PPT)
高中数学苏教版必修第二册
第9章 平面向量
9.2 向量运算
9.2.1向量的加减法
第1课时 向量的加法
课标阐释
1.理解向量加法的概念以及向量加法的几何意义.(数学抽象、直观想象)
2.掌握向量加法的平行四边形法则和三角形法则,会进行向量的加法运算.(数学抽象、数学运算)
3.掌握向量加法的交换律和结合律,会用它们进行计算.(数学运算、逻辑推理)
思维脉络
【激趣诱思】
我们是否可以根据飞机从甲地飞往乙地的方向与距离以及从乙地飞往丙地的方向与距离来确定甲地到丙地的方向与距离呢
【知识梳理】
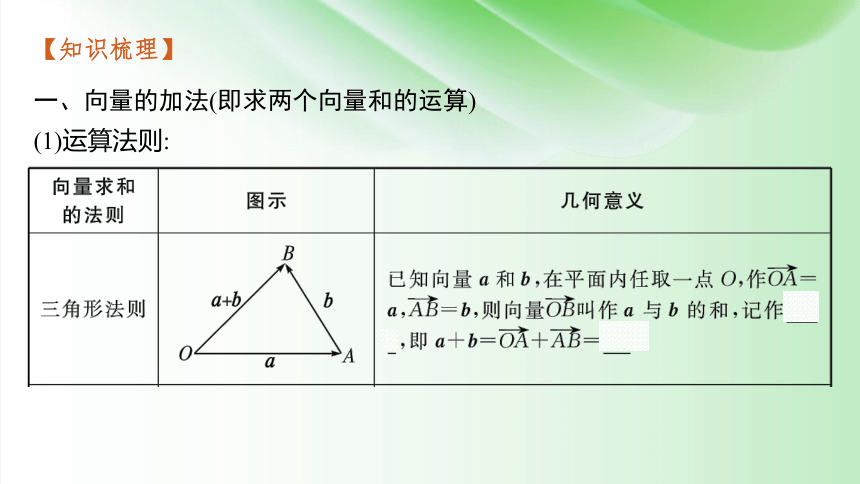
一、向量的加法(即求两个向量和的运算)
(1)运算法则:
(2)任一向量与其相反向量的和是零向量,即a+(-a)=0.
(3)规定:对于零向量和任一向量a满足a+0=0+a=a.
名师点析 向量加法的平行四边形法则和三角形法则的区别与联系
区别:(1)三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;(2)三角形法则适用于所有的两个非零向量求和,而平行四边形法则仅适用于不共线的两个非零向量求和.
联系:三角形法则作出的图形是平行四边形法则作出图形的一半,当两个向量不共线时,两种加法法则在本质上是一致的.
微练习
答案 (1)C (2)0
微思考
二、向量加法的运算律
向量加法的运算律与实数加法的运算律相同,可类比记忆.
(1)交换律:a+b=b+a.
(2)结合律:(a+b)+c=a+(b+c).
名师点析 |a+b|与|a|,|b|之间的关系
对任意两个向量a,b,有|a+b|≤|a|+|b|,当且仅当a,b方向相同时等号成立.
微练习
已知非零向量a,b,c,则向量(a+c)+b,b+(a+c),b+(c+a),c+(b+a),c+(a+b)中,与向量a+b+c相等的个数为( )
A.2 B.3 C.4 D.5
答案 D
解析 由向量加法的交换律与结合律可知,所给的5个向量都与a+b+c相等.
探究一
向量加法法则的应用
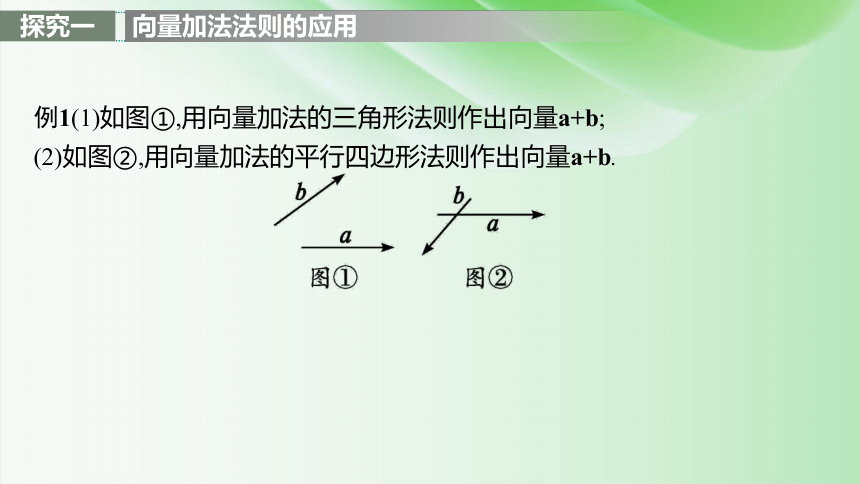
例1(1)如图①,用向量加法的三角形法则作出向量a+b;
(2)如图②,用向量加法的平行四边形法则作出向量a+b.
图①
图②
反思感悟 用向量加法的三角形法则求和向量,关键是抓住“首尾相连”,和向量是第一个向量的起点指向第二个向量的终点.用向量加法的平行四边形法则应注意“共起点”.两种方法中,第一个向量的起点可任意选取.
变式训练1如图,已知向量a,b,c,求作向量a+b+c.
探究二
向量的加法及运算律
例2化简:
反思感悟 向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
探究三
向量加法在实际问题中的应用
例3在静水中船的速度为20 m/min,水流的速度为10 m/min.如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
解 作出图形,如图.船速v船与岸的方向成α角,由图可知v水+v船=v实际,结合已知条件,四边形ABCD为平行四边形.
在Rt△ACD中,
所以α=60°,从而船与水流方向成120°的角.
故船行进的方向是与水流的方向成120°的角的方向.
反思感悟 应用向量解决平面几何问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.
延伸探究 1若例3条件不变,则经过3 h,该船的实际航程是多少千米
延伸探究 2若例3条件不变,改为若船沿垂直于水流的方向航行,求船实际行进的方向与河岸的夹角的正切值.
解
变式训练3一架救援直升机从A地沿北偏东60°方向飞行了40 km到达B地,再由B地沿正北方向飞行40 km到达C地,求此时直升机与A地的相对位置.
素养形成
方法点睛 (1)本题主要考查向量加法的多边形法则和零向量.由于正n边形绕圆心O旋转 角度时,虽然各向量方向都改变了,但模没有改变,正n边形的位置不变,其和向量也没有改变,由此判断和向量为0.
(2)零向量的方向是任意的,且零向量的模为0.
当堂检测
答案 C
答案 B
答案 A
高中数学苏教版必修第二册
第9章 平面向量
9.2 向量运算
9.2.1向量的加减法
第2课时 向量的减法
课标阐释
1.借助实例和平面向量的几何表示,理解向量减法的意义.(几何直观、数学抽象)
2.能熟练地进行向量的加减综合运算.(数学运算)
思维脉络
【激趣诱思】
一架飞机由北京飞往上海,然后再由上海返回北京,我们把北京记作A点,上海记作B点,那么这辆飞机的位移是多少 怎样用向量来表示呢
【知识梳理】
向量的减法
(1)定义:若b+x=a,则向量x叫作a与b的差,记为 a-b .求两个 向量差的运算 ,叫作向量的减法.
(2)几何意义:当向量a,b起点相同时,a-b表示为从b的终点指向a的终点的向量.
也可以理解成从减向量的终点指向被减向量的终点
(4)减去一个向量等于加上这个向量的相反向量.
名师点析 (1)若向量a,b为非零不共线向量,则a,b与a-b围成三角形,故称这种作两向量差的方法为向量减法的三角形法则.
(2)求两个向量的差就是要把两个向量的始点放在一起,它们的差是以减向量的终点为始点,以被减向量的终点为终点的向量,可简记为“共始点,连终点,指向被减”.
微判断
(1)两个向量的差仍是一个向量.( )
(2)向量a与向量b的差与向量b与向量a的差互为相反向量.( )
√
√
微练习
答案 (1)C (2)B
微思考
||a|-|b||≤|a-b|≤|a|+|b|中,等号何时成立
提示 ①当向量a,b不共线时,||a|-|b||<|a-b|<|a|+|b|;
②当向量a,b共线且同向时,前一个等号成立;当向量a,b共线且反向时,后一个等号成立.
探究一
向量减法法则的运用
例1
如图所示,已知向量a,b,c,d,求作向量a-b,c-d.
解
变式训练1如图,已知向量a,b,c不共线,求作向量a+b-c.
反思感悟 求作两个向量的差向量时,若两个向量有共同起点,直接连接两个向量的终点,并指向被减向量,就得到两个向量的差向量;若两个向量的起点不重合,先通过平移使它们的起点重合,再作出差向量.
探究二
向量的加法与减法运算
反思感悟 1.向量减法运算的常用方法
2.向量加减法化简的两种形式
(1)首尾相连且为和;
(2)起点相同且为差.
做题时要注意观察是否有这两种形式,同时要注意逆向应用.
探究三
向量减法的应用
反思感悟 用向量表示其他向量的方法
(1)解决此类问题要充分利用平面几何知识,灵活运用平行四边形法则和三角形法则.
(2)表示向量时要考虑以下问题:它是某个平行四边形的对角线吗 是否可以找到由起点到终点的恰当途径 它的起点和终点是否是两个有共同起点的向量的终点
(3)必要时可以直接用向量求和的多边形法则.
延伸探究 2本例中的条件“点B是平行四边形ACDE外一点”若换为“点B是平行四边形ACDE内一点”,其他条件不变,其结论又如何呢
素养形成
利用已知向量表示未知向量
典例 如图,解答下列各题:
方法点睛 利用已知向量表示其他向量的一个关键及三点注意
(1)一个关键
关键是确定已知向量与被表示向量的转化渠道.
(2)三点注意
①注意相等向量、相反向量、共线向量以及构成三角形三向量之间的关系;
②注意应用向量加法、减法的几何意义以及它们的运算律;
③注意在封闭图形中利用多边形法则.
当堂检测
1.若非零向量a,b互为相反向量,则下列说法错误的是( )
A.a∥b B.a≠b
C.|a|≠|b| D.b=-a
答案 C
解析 根据相反向量的定义,大小相等,方向相反,可知|a|=|b|.
答案 C
A.平行四边形 B.菱形
C.矩形 D.梯形
答案 A
A.a-b+c
B.b-(a+c)
C.a+b+c
D.b-a+c
答案 A
答案 0
谢谢观看
高中数学苏教版必修第二册
第9章 平面向量
9.2 向量运算
9.2.1向量的加减法
第1课时 向量的加法
课标阐释
1.理解向量加法的概念以及向量加法的几何意义.(数学抽象、直观想象)
2.掌握向量加法的平行四边形法则和三角形法则,会进行向量的加法运算.(数学抽象、数学运算)
3.掌握向量加法的交换律和结合律,会用它们进行计算.(数学运算、逻辑推理)
思维脉络
【激趣诱思】
我们是否可以根据飞机从甲地飞往乙地的方向与距离以及从乙地飞往丙地的方向与距离来确定甲地到丙地的方向与距离呢
【知识梳理】
一、向量的加法(即求两个向量和的运算)
(1)运算法则:
(2)任一向量与其相反向量的和是零向量,即a+(-a)=0.
(3)规定:对于零向量和任一向量a满足a+0=0+a=a.
名师点析 向量加法的平行四边形法则和三角形法则的区别与联系
区别:(1)三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;(2)三角形法则适用于所有的两个非零向量求和,而平行四边形法则仅适用于不共线的两个非零向量求和.
联系:三角形法则作出的图形是平行四边形法则作出图形的一半,当两个向量不共线时,两种加法法则在本质上是一致的.
微练习
答案 (1)C (2)0
微思考
二、向量加法的运算律
向量加法的运算律与实数加法的运算律相同,可类比记忆.
(1)交换律:a+b=b+a.
(2)结合律:(a+b)+c=a+(b+c).
名师点析 |a+b|与|a|,|b|之间的关系
对任意两个向量a,b,有|a+b|≤|a|+|b|,当且仅当a,b方向相同时等号成立.
微练习
已知非零向量a,b,c,则向量(a+c)+b,b+(a+c),b+(c+a),c+(b+a),c+(a+b)中,与向量a+b+c相等的个数为( )
A.2 B.3 C.4 D.5
答案 D
解析 由向量加法的交换律与结合律可知,所给的5个向量都与a+b+c相等.
探究一
向量加法法则的应用
例1(1)如图①,用向量加法的三角形法则作出向量a+b;
(2)如图②,用向量加法的平行四边形法则作出向量a+b.
图①
图②
反思感悟 用向量加法的三角形法则求和向量,关键是抓住“首尾相连”,和向量是第一个向量的起点指向第二个向量的终点.用向量加法的平行四边形法则应注意“共起点”.两种方法中,第一个向量的起点可任意选取.
变式训练1如图,已知向量a,b,c,求作向量a+b+c.
探究二
向量的加法及运算律
例2化简:
反思感悟 向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
探究三
向量加法在实际问题中的应用
例3在静水中船的速度为20 m/min,水流的速度为10 m/min.如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
解 作出图形,如图.船速v船与岸的方向成α角,由图可知v水+v船=v实际,结合已知条件,四边形ABCD为平行四边形.
在Rt△ACD中,
所以α=60°,从而船与水流方向成120°的角.
故船行进的方向是与水流的方向成120°的角的方向.
反思感悟 应用向量解决平面几何问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.
延伸探究 1若例3条件不变,则经过3 h,该船的实际航程是多少千米
延伸探究 2若例3条件不变,改为若船沿垂直于水流的方向航行,求船实际行进的方向与河岸的夹角的正切值.
解
变式训练3一架救援直升机从A地沿北偏东60°方向飞行了40 km到达B地,再由B地沿正北方向飞行40 km到达C地,求此时直升机与A地的相对位置.
素养形成
方法点睛 (1)本题主要考查向量加法的多边形法则和零向量.由于正n边形绕圆心O旋转 角度时,虽然各向量方向都改变了,但模没有改变,正n边形的位置不变,其和向量也没有改变,由此判断和向量为0.
(2)零向量的方向是任意的,且零向量的模为0.
当堂检测
答案 C
答案 B
答案 A
高中数学苏教版必修第二册
第9章 平面向量
9.2 向量运算
9.2.1向量的加减法
第2课时 向量的减法
课标阐释
1.借助实例和平面向量的几何表示,理解向量减法的意义.(几何直观、数学抽象)
2.能熟练地进行向量的加减综合运算.(数学运算)
思维脉络
【激趣诱思】
一架飞机由北京飞往上海,然后再由上海返回北京,我们把北京记作A点,上海记作B点,那么这辆飞机的位移是多少 怎样用向量来表示呢
【知识梳理】
向量的减法
(1)定义:若b+x=a,则向量x叫作a与b的差,记为 a-b .求两个 向量差的运算 ,叫作向量的减法.
(2)几何意义:当向量a,b起点相同时,a-b表示为从b的终点指向a的终点的向量.
也可以理解成从减向量的终点指向被减向量的终点
(4)减去一个向量等于加上这个向量的相反向量.
名师点析 (1)若向量a,b为非零不共线向量,则a,b与a-b围成三角形,故称这种作两向量差的方法为向量减法的三角形法则.
(2)求两个向量的差就是要把两个向量的始点放在一起,它们的差是以减向量的终点为始点,以被减向量的终点为终点的向量,可简记为“共始点,连终点,指向被减”.
微判断
(1)两个向量的差仍是一个向量.( )
(2)向量a与向量b的差与向量b与向量a的差互为相反向量.( )
√
√
微练习
答案 (1)C (2)B
微思考
||a|-|b||≤|a-b|≤|a|+|b|中,等号何时成立
提示 ①当向量a,b不共线时,||a|-|b||<|a-b|<|a|+|b|;
②当向量a,b共线且同向时,前一个等号成立;当向量a,b共线且反向时,后一个等号成立.
探究一
向量减法法则的运用
例1
如图所示,已知向量a,b,c,d,求作向量a-b,c-d.
解
变式训练1如图,已知向量a,b,c不共线,求作向量a+b-c.
反思感悟 求作两个向量的差向量时,若两个向量有共同起点,直接连接两个向量的终点,并指向被减向量,就得到两个向量的差向量;若两个向量的起点不重合,先通过平移使它们的起点重合,再作出差向量.
探究二
向量的加法与减法运算
反思感悟 1.向量减法运算的常用方法
2.向量加减法化简的两种形式
(1)首尾相连且为和;
(2)起点相同且为差.
做题时要注意观察是否有这两种形式,同时要注意逆向应用.
探究三
向量减法的应用
反思感悟 用向量表示其他向量的方法
(1)解决此类问题要充分利用平面几何知识,灵活运用平行四边形法则和三角形法则.
(2)表示向量时要考虑以下问题:它是某个平行四边形的对角线吗 是否可以找到由起点到终点的恰当途径 它的起点和终点是否是两个有共同起点的向量的终点
(3)必要时可以直接用向量求和的多边形法则.
延伸探究 2本例中的条件“点B是平行四边形ACDE外一点”若换为“点B是平行四边形ACDE内一点”,其他条件不变,其结论又如何呢
素养形成
利用已知向量表示未知向量
典例 如图,解答下列各题:
方法点睛 利用已知向量表示其他向量的一个关键及三点注意
(1)一个关键
关键是确定已知向量与被表示向量的转化渠道.
(2)三点注意
①注意相等向量、相反向量、共线向量以及构成三角形三向量之间的关系;
②注意应用向量加法、减法的几何意义以及它们的运算律;
③注意在封闭图形中利用多边形法则.
当堂检测
1.若非零向量a,b互为相反向量,则下列说法错误的是( )
A.a∥b B.a≠b
C.|a|≠|b| D.b=-a
答案 C
解析 根据相反向量的定义,大小相等,方向相反,可知|a|=|b|.
答案 C
A.平行四边形 B.菱形
C.矩形 D.梯形
答案 A
A.a-b+c
B.b-(a+c)
C.a+b+c
D.b-a+c
答案 A
答案 0
谢谢观看
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
