13.2.2 空间两条直线的位置关系 课件(共58张PPT) 2023-2024学年高中数学苏教版必修第二册
文档属性
| 名称 | 13.2.2 空间两条直线的位置关系 课件(共58张PPT) 2023-2024学年高中数学苏教版必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:55:32 | ||
图片预览









文档简介
(共58张PPT)
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.2 空间两条直线的位置关系
第1课时 平行直线
课标阐释
1.了解基本事实4和等角定理.(数学抽象)
2.借助长方体,通过直观感知,了解空间中直线与直线的位置关系.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
如图,在长方体ABCD-A'B'C'D'中,BB'∥AA',DD'∥AA',BB'与DD'平行吗
【知识梳理】
一、空间中直线与直线的位置关系
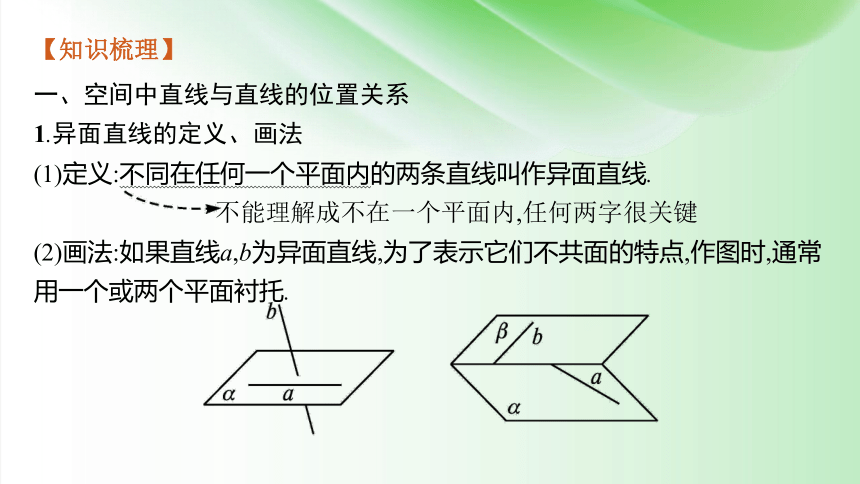
1.异面直线的定义、画法
(1)定义:不同在任何一个平面内的两条直线叫作异面直线.
不能理解成不在一个平面内,任何两字很关键
(2)画法:如果直线a,b为异面直线,为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托.
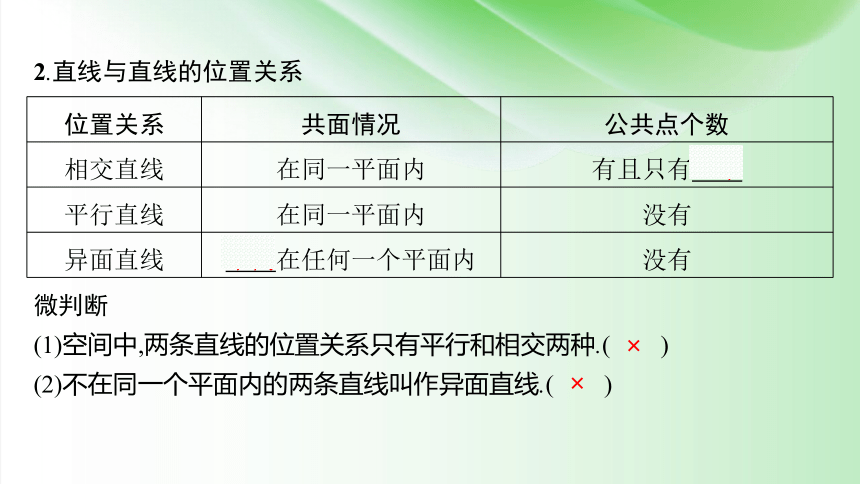
2.直线与直线的位置关系
位置关系 共面情况 公共点个数
相交直线 在同一平面内 有且只有一个
平行直线 在同一平面内 没有
异面直线 不同在任何一个平面内 没有
微判断
(1)空间中,两条直线的位置关系只有平行和相交两种.( )
(2)不在同一个平面内的两条直线叫作异面直线.( )
×
×
二、平行直线
1.基本事实4
平行于同一条直线的两条直线平行.
2.等角定理
如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.
名师点析 如果一个角的两边与另一个角的两边分别平行,并且一边的方向相同,另一边的方向相反,那么这两个角互补.
微判断
(1)垂直于同一直线的两条直线互相平行.( )
(2)分别和两条异面直线平行的两条直线平行.( )
(3)如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.( )
×
×
√
微练习
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
A.30° B.30°或150°
C.150° D.以上结论都不对
答案 B
微思考
如果两条直线和第三条直线成等角,那么这两条直线平行吗
提示 不一定.这两条直线可能相交、平行或异面.
探究一
空间两直线位置关系的判定
例1如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,CC1的中点,有以下四个结论:①直线DM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为 (填序号).
答案 ①③④
解析 ①中直线DM与直线CC1不平行,且在同一平面内,故它们延长后必相交,故结论正确;③④中的两条直线既不相交又不平行,即均为异面直线,故结论正确;②中AM与BN是异面直线,故②不正确.
反思感悟 1.判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用基本事实4判断.
2.判定两条直线是异面直线有定义法和排除法,由于使用定义判断不方便,故常用排除法,即说明这两条直线不平行、不相交,则它们异面.
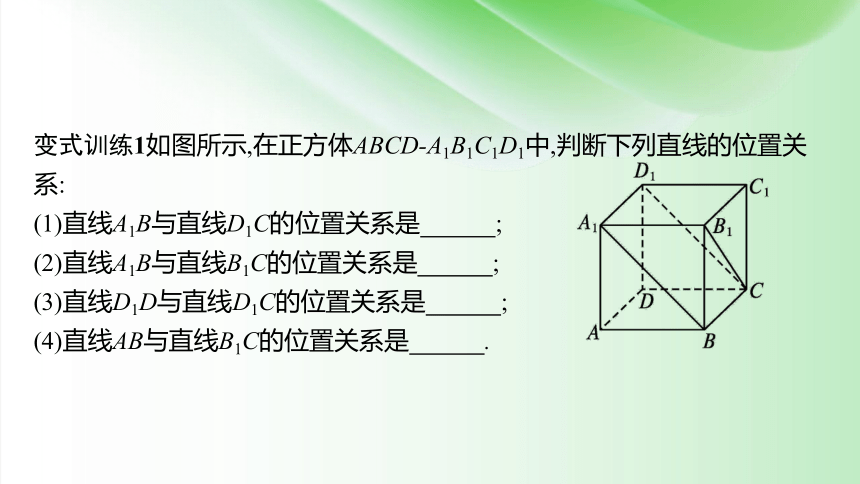
变式训练1如图所示,在正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:
(1)直线A1B与直线D1C的位置关系是 ;
(2)直线A1B与直线B1C的位置关系是 ;
(3)直线D1D与直线D1C的位置关系是 ;
(4)直线AB与直线B1C的位置关系是 .
答案 (1)平行 (2)异面 (3)相交 (4)异面
序号 结论 理由
(1) 平行 因为A1D1 BC,所以四边形A1BCD1为平行四边形,A1B∥D1C
(2) 异面 A1B与B1C不同在任何一个平面内
(3) 相交 D1D∩D1C=D1
(4) 异面 AB与B1C不同在任何一个平面内
探究二
直线与直线平行的证明
例2如图所示,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)如果AC=BD,求证:四边形EFGH是菱形.
证明 (1)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EF∥AC,HG∥AC,EF=HG= AC,
所以EF∥HG,EF=HG,
所以四边形EFGH是平行四边形.
(2)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EH∥BD,EH= BD.
因为EF= AC,AC=BD,所以EH=EF.
又因为EFGH是平行四边形,所以四边形EFGH是菱形.
技巧方法 证明两直线平行,目前有两种途径:一是应用基本事实4,即找到第三条直线,证明这两条直线都与之平行;二是证明同一个平面内这两条直线无公共点.
变式训练2在正方体ABCD-A'B'C'D'中,E,F,E',F'分别是AB,BC,A'B',B'C'的中点,求证:EE'∥FF'.
证明 因为E,E'分别是AB,A'B'的中点,
所以BE∥B'E',且BE=B'E'.
所以四边形EBB'E'是平行四边形,
所以EE'∥BB',同理可证FF'∥BB'.所以EE'∥FF'.
探究三
等角定理的应用
例3如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱
AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠B1M1C1=∠BMC.
分析(1)通过基本事实4证明MM1∥BB1,且MM1=BB1.(2)由(1)知B1M1∥BM,同理证得C1M1∥CM,再由等角定理证得∠BMC=∠B1M1C1;也可以通过证明△BCM≌△B1C1M1证出∠BMC=∠B1M1C1.
证明 (1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,∴MM1 AA1.
又AA1 BB1,∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.
(2)由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.
∴∠BMC=∠B1M1C1.
要点笔记 有关证明角相等问题,一般采用下面三种途径:
(1)利用等角定理.
(2)利用三角形相似.
(3)利用三角形全等.本例是通过第一种途径来实现的.
延伸探究 将例3中的条件“M,M1分别是棱AD和A1D1的中点”改为“M,N分别是棱CD,AD的中点”,其他条件不变,求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
证明 (1)如图,连接AC,
在△ACD中,∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,∴MN∥AC,MN= AC.
由正方体的性质,得AC∥A1C1,AC=A1C1.
∴MN∥A1C1,且MN= A1C1,即MN≠A1C1,
∴四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,
又ND∥A1D1,∴∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
∴∠DNM=∠D1A1C1.
素养形成
等角定理的综合应用
典例 若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1方向相同,则下列结论正确的是( )
A.OB∥O1B1,且方向相同
B.OB∥O1B1,方向可能不同
C.OB与O1B1不平行
D.OB与O1B1不一定平行
答案 D
解析 当∠AOB=∠A1O1B1,且OA∥O1A1时,OA与O1A1的方向相同,OB与O1B1不一定平行,如图所示,故选D.
方法点睛 在讨论空间中两条直线平行的位置关系时,除了运用等角定理,也可以利用数形结合思想.
当堂检测
1.如果OA∥O1A1,OB∥O1B1,那么∠AOB与∠A1O1B1( )
A.相等 B.互补
C.相等或互补 D.以上均不对
答案 C
解析 由题意,两角对应边平行,如果方向均相同或相反,那么两角相等,如果一组对应边方向相同,另一组对应边方向相反,那么两角互补.
2.直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
答案 D
解析 如图所示,长方体ABCD-A1B1C1D1中,AB与AA1相交,
A1B1与AA1相交,AB∥A1B1;AD与AA1相交,AB与AD相交,
AA1与AB相交;A1D1与AA1相交,AB与AA1相交,
AB与A1D1异面.
3.如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是B1O和C1O的中点,则长方体的各棱中与EF平行的有( )
A.3条
B.4条
C.5条
D.6条
答案 B
解析 EF∥B1C1,EF∥BC,EF∥AD,EF∥A1D1.
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.2 空间两条直线的位置关系
第2课时 异面直线
课标阐释
1.借助长方体,通过直观感知,了解空间中直线与直线的位置关系.(几何直观)
2.掌握两异面直线所成的角的求法.(几何直观、数学运算)
思维脉络
【激趣诱思】
随着世界各国经济的发展和高速公路的出现,现代化的城市道路交通开始朝立体化发展.立体交叉桥,简称立交桥.世界上第一座立交桥是于1928年由美国建造的,此后世界各地的立交桥相继出现.1952年,我国于
北京滨河路兴建了首座立交桥.我国第二座立交桥是于1962年在广州修建的.现在的立交桥已由最初的上、下两层分开式,向多层次、多方向的复杂立体交叉方式发展,目的是大力提高交叉路口的车流速度,并确保交通安全.若把立交桥抽象成直线,它们在同一个平面内吗 这样的直线有何特征 一条南北走向和一条东西走向(不同层)的立交桥所在直线的夹角如何刻画
【知识梳理】
一、定理
过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
微练习
异面直线是指( )
A.空间中两条不相交的直线
B.分别位于两个不同平面内的两条直线
C.平面内的一条直线与平面外的一条直线
D.不同在任何一个平面内的两条直线
答案 D
解析 对于A,空间中两条不相交的直线有两种可能,一是平行(共面),另一个是异面.所以A应排除.对于B,分别位于两个不同平面内的两条直线,既可能平行也可能相交也可能异面,如图,就是相交的情况,所以B应排除.对于C,如图的a,b可看作是平面α内的一条直线a与平面α外的一条直线b,显然它们是相交直线,所以C应排除.D符合定义.
二、异面直线所成的角
(1)定义
如图,a与b是异面直线,经过空间任意一点O,作直线a'∥a,b'∥b,我们把直线a'和b'所成的锐角(或直角)叫作异面直线a,b所成的角或夹角.
(2)两条异面直线所成角的取值范围: .
(3)若异面直线a,b所成的角是直角,则称异面直线a,b互相垂直,记作a⊥b.
微判断
(1)异面直线所成的角的大小与O点的位置有关,即O点位置不同时,这一角的大小也不同.( )
(2)异面直线a与b所成角可以是0°.( )
(3)如果两条平行直线中的一条与某一条直线垂直,那么另一条直线也与这条直线垂直.( )
×
×
√
微练习
如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是 ;
(2)AC和D1C1所成的角是 ;
(3)AC和B1D1所成的角是 ;
(4)AC和A1B所成的角是 .
答案 (1)90° (2)45° (3)90° (4)60°
解析 (1)根据正方体的性质可得AC和DD1所成的角是90°.
(2)∵D1C1∥DC,∴∠ACD即为AC和D1C1所成的角,由正方体的性质得∠ACD=45°.
(3)∵BD∥B1D1,BD⊥AC,∴B1D1⊥AC,即AC和B1D1所成的角是90°.
(4)∵A1B∥D1C,△ACD1是等边三角形,∴AC和A1B所成的角是60°.
探究一
异面直线的判定
例1如图,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有 (填序号).
答案 ②④
解析 如题干图①中,GH∥MN.图②中,G,H,N三点共面,但M 平面GHN,因此直线GH与MN异面.图③中,连接GM,GM∥HN,因此,GH与MN共面.图④中,G,M,N三点共面,但H 平面GMN,因此GH与MN异面.所以图②,④中GH与MN异面.
技巧方法 判定两条直线是异面直线的方法
(1)证明两条直线既不平行又不相交.
(2)定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,B l,l α,则AB与l是异面直线(如图).
变式训练1(多选)
如图,E,F是AD上互异的两点,G,H是BC上互异的两点,由图可知,其中叙述正确的是( )
A.AB与CD互为异面直线
B.FH分别与DC,DB互为异面直线
C.EG与FH互为异面直线
D.EG与AB互为异面直线
答案 AC
解析 AB与平面BCD交于点B,且B CD,故AB与CD互为异面直线,故A正确.当H点落在C或F落在D点上时,FH与CD相交;当H落在B或F点落在D上时,FH与DB相交,故B错误.FH与平面EGD交于F点,而F EG,H 平面EGD,故EG与FH互为异面直线,故C正确.当G落在B上或E落在A上时,EG与AB相交,故D错误.所以A,C正确.
探究二
直线与直线垂直的证明
例2在直三棱柱ABC-A1B1C1中,AC⊥BC,求证:AC⊥BC1.
证明 如图,连接A1B,设A1C1=a,B1C1=b,AA1=h,因为三棱柱ABC-A1B1C1是直三棱柱,
所以∠BB1C1=∠A1AB=90°,
所以 =b2+h2,AB2=a2+b2,
A1B2=a2+b2+h2,
所以A1B2= ,
则A1C1⊥BC1,即∠A1C1B=90°.
又因为AC∥A1C1,所以∠A1C1B就是直线AC与BC1所成的角,所以AC⊥BC1.
技巧方法 证明空间的两条直线垂直的方法
(1)定义法:利用两条直线所成的角为90°证明两直线垂直.
(2)平面几何图形性质法:利用勾股定理、菱形的对角线相互垂直、等腰三角形(等边三角形)底边的中线和底边垂直等.
变式训练2如图,正方体ABCD-A1B1C1D1,求证:AC⊥B1D.
证明 如图,连接BD,交AC于O,设BB1的中点为E,
连接OE,则OE∥DB1,
所以OE与AC所成的角即为DB1与AC所成的角.
连接AE,CE,易证AE=CE,
又O是AC的中点,所以AC⊥OE,所以AC⊥B1D.
探究三
异面直线所成的角
角度1 求异面直线所成的角
例3在空间四边形ABCD中,AB=CD,且AB与CD所成锐角为30°,E,F分别为BC,AD的中点,求EF与AB所成角的大小.
解 如图所示,取AC的中点G,连接EG,FG,
则EG∥AB且EG= AB,GF∥CD且GF= CD.
由AB=CD知EG=FG,
从而可知∠GEF为EF与AB所成的角,
∠EGF或其补角为AB与CD所成的角.
∵AB与CD所成角为30°,∴∠EGF=30°或150°,
由EG=FG知△EFG为等腰三角形,当∠EGF=30°时,∠GEF=75°,当∠EGF=150°时,∠GEF=15°,
故EF与AB所成角的大小为15°或75°.
角度2 由异面直线所成角的大小求线段的长
例4如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2,求EF的长度.
解 取BC的中点M,连接ME,MF,如图.则ME∥AC,MF∥BD,
∴ME与MF所成的锐角(或直角)即为AC与BD所成的角,而AC,BD所成的角为60°,∴∠EMF=60°或∠EMF=120°.
规律总结 求两条异面直线所成的角的一般步骤
(1)构造角:根据异面直线的定义,通过作平行线或平移直线,作出异面直线夹角的相关角.
(2)计算角:求角度,常利用三角形.
(3)确定角:若求出的角是锐角或是直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
变式训练3如图所示,在正方体ABCD-A1B1C1D1中.
(1)求A1C1与B1C所成角的大小;
(2)若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.
解 (1)如图所示,连接AC,AB1.
由六面体ABCD-A1B1C1D1是正方体知,四边形AA1C1C为平行四边形,∴AC∥A1C1,从而B1C与AC所成的角就是A1C1与B1C所成的角.
在△AB1C中,由AB1=AC=B1C,可知∠B1CA=60°,
即A1C1与B1C所成的角为60°.
(2)如图所示,连接BD.由(1)知AC∥A1C1,
∴AC与EF所成的角就是A1C1与EF所成的角.
∵EF是△ABD的中位线,∴EF∥BD.
又AC⊥BD,∴AC⊥EF,∴EF⊥A1C1,
即A1C1与EF所成的角为90°.
素养形成
一题多解——异面直线的夹角问题
典例 如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
分析要求异面直线所成角的大小,关键是作出异面直线所成的角,把它归结到三角形中,通过解三角形就可以得出答案.同时在解题时要注意异面直线所成角的范围.
解法一(直接平移法)如图所示.
连接A1C1,B1D1交于点O,取DD1的中点G,连接GA1,GC1,OG,则OG∥B1D,EF∥A1C1,故∠GOA1或其补角就是异面直线DB1与EF所成的角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
解法二(中位线平移法)如图所示.
解法三如图所示,分别取AA1,CC1的中点M,N,连接MN,
则MN∥EF,所以直线MN与DB1所成的角就是异面直线DB1与EF所成的角.
连接MB1,DN,DM,B1N,则B1N∥DM,且B1N=DM,
∴四边形DMB1N为平行四边形,
∴MN与B1D必相交,设交点为P.
∴DM2=DP2+MP2,
∴∠DPM=90°,即DB1⊥EF,
∴异面直线DB1与EF所成的角为90°.
解法四(补形法)
如图所示,在原正方体的右侧补上一个同样的正方体,连接B1Q,DQ,则B1Q∥EF.
于是∠DB1Q或其补角就是异面直线DB1与EF所成的角,通过计算,不难得到B1D2+B1Q2=DQ2,故异面直线DB1与EF所成的角为90°.
反思感悟 (1)求两异面直线所成的角的三个步骤
①作:根据所成角的定义,用平移法作出异面直线所成的角;
②证:证明作出的角就是要求的角;
③计算:求角的值,常利用解三角形得出.
可用“一作二证三计算”来概括.注意异面直线所成角范围是0°<θ≤90°.
(2)求异面直线所成的角,关键是找出异面直线所成的角,这就需要借助于几何图形,探索和论述某角是异面直线所成的角.“找角”的方法可以利用直接平移法,也可以通过补体法,最后归结为三角形中计算角度;若夹角是直角,除了计算出直角,还可以用后面的证明垂直加以解决.本例充分体现了逻辑推理与数学运算的数学核心素养及化归数学思想的应用.
谢谢观看
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.2 空间两条直线的位置关系
第1课时 平行直线
课标阐释
1.了解基本事实4和等角定理.(数学抽象)
2.借助长方体,通过直观感知,了解空间中直线与直线的位置关系.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
如图,在长方体ABCD-A'B'C'D'中,BB'∥AA',DD'∥AA',BB'与DD'平行吗
【知识梳理】
一、空间中直线与直线的位置关系
1.异面直线的定义、画法
(1)定义:不同在任何一个平面内的两条直线叫作异面直线.
不能理解成不在一个平面内,任何两字很关键
(2)画法:如果直线a,b为异面直线,为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托.
2.直线与直线的位置关系
位置关系 共面情况 公共点个数
相交直线 在同一平面内 有且只有一个
平行直线 在同一平面内 没有
异面直线 不同在任何一个平面内 没有
微判断
(1)空间中,两条直线的位置关系只有平行和相交两种.( )
(2)不在同一个平面内的两条直线叫作异面直线.( )
×
×
二、平行直线
1.基本事实4
平行于同一条直线的两条直线平行.
2.等角定理
如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.
名师点析 如果一个角的两边与另一个角的两边分别平行,并且一边的方向相同,另一边的方向相反,那么这两个角互补.
微判断
(1)垂直于同一直线的两条直线互相平行.( )
(2)分别和两条异面直线平行的两条直线平行.( )
(3)如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.( )
×
×
√
微练习
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
A.30° B.30°或150°
C.150° D.以上结论都不对
答案 B
微思考
如果两条直线和第三条直线成等角,那么这两条直线平行吗
提示 不一定.这两条直线可能相交、平行或异面.
探究一
空间两直线位置关系的判定
例1如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,CC1的中点,有以下四个结论:①直线DM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为 (填序号).
答案 ①③④
解析 ①中直线DM与直线CC1不平行,且在同一平面内,故它们延长后必相交,故结论正确;③④中的两条直线既不相交又不平行,即均为异面直线,故结论正确;②中AM与BN是异面直线,故②不正确.
反思感悟 1.判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用基本事实4判断.
2.判定两条直线是异面直线有定义法和排除法,由于使用定义判断不方便,故常用排除法,即说明这两条直线不平行、不相交,则它们异面.
变式训练1如图所示,在正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:
(1)直线A1B与直线D1C的位置关系是 ;
(2)直线A1B与直线B1C的位置关系是 ;
(3)直线D1D与直线D1C的位置关系是 ;
(4)直线AB与直线B1C的位置关系是 .
答案 (1)平行 (2)异面 (3)相交 (4)异面
序号 结论 理由
(1) 平行 因为A1D1 BC,所以四边形A1BCD1为平行四边形,A1B∥D1C
(2) 异面 A1B与B1C不同在任何一个平面内
(3) 相交 D1D∩D1C=D1
(4) 异面 AB与B1C不同在任何一个平面内
探究二
直线与直线平行的证明
例2如图所示,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)如果AC=BD,求证:四边形EFGH是菱形.
证明 (1)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EF∥AC,HG∥AC,EF=HG= AC,
所以EF∥HG,EF=HG,
所以四边形EFGH是平行四边形.
(2)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EH∥BD,EH= BD.
因为EF= AC,AC=BD,所以EH=EF.
又因为EFGH是平行四边形,所以四边形EFGH是菱形.
技巧方法 证明两直线平行,目前有两种途径:一是应用基本事实4,即找到第三条直线,证明这两条直线都与之平行;二是证明同一个平面内这两条直线无公共点.
变式训练2在正方体ABCD-A'B'C'D'中,E,F,E',F'分别是AB,BC,A'B',B'C'的中点,求证:EE'∥FF'.
证明 因为E,E'分别是AB,A'B'的中点,
所以BE∥B'E',且BE=B'E'.
所以四边形EBB'E'是平行四边形,
所以EE'∥BB',同理可证FF'∥BB'.所以EE'∥FF'.
探究三
等角定理的应用
例3如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱
AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠B1M1C1=∠BMC.
分析(1)通过基本事实4证明MM1∥BB1,且MM1=BB1.(2)由(1)知B1M1∥BM,同理证得C1M1∥CM,再由等角定理证得∠BMC=∠B1M1C1;也可以通过证明△BCM≌△B1C1M1证出∠BMC=∠B1M1C1.
证明 (1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,∴MM1 AA1.
又AA1 BB1,∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.
(2)由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
由(1)同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.
∴∠BMC=∠B1M1C1.
要点笔记 有关证明角相等问题,一般采用下面三种途径:
(1)利用等角定理.
(2)利用三角形相似.
(3)利用三角形全等.本例是通过第一种途径来实现的.
延伸探究 将例3中的条件“M,M1分别是棱AD和A1D1的中点”改为“M,N分别是棱CD,AD的中点”,其他条件不变,求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
证明 (1)如图,连接AC,
在△ACD中,∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,∴MN∥AC,MN= AC.
由正方体的性质,得AC∥A1C1,AC=A1C1.
∴MN∥A1C1,且MN= A1C1,即MN≠A1C1,
∴四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,
又ND∥A1D1,∴∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
∴∠DNM=∠D1A1C1.
素养形成
等角定理的综合应用
典例 若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1方向相同,则下列结论正确的是( )
A.OB∥O1B1,且方向相同
B.OB∥O1B1,方向可能不同
C.OB与O1B1不平行
D.OB与O1B1不一定平行
答案 D
解析 当∠AOB=∠A1O1B1,且OA∥O1A1时,OA与O1A1的方向相同,OB与O1B1不一定平行,如图所示,故选D.
方法点睛 在讨论空间中两条直线平行的位置关系时,除了运用等角定理,也可以利用数形结合思想.
当堂检测
1.如果OA∥O1A1,OB∥O1B1,那么∠AOB与∠A1O1B1( )
A.相等 B.互补
C.相等或互补 D.以上均不对
答案 C
解析 由题意,两角对应边平行,如果方向均相同或相反,那么两角相等,如果一组对应边方向相同,另一组对应边方向相反,那么两角互补.
2.直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
答案 D
解析 如图所示,长方体ABCD-A1B1C1D1中,AB与AA1相交,
A1B1与AA1相交,AB∥A1B1;AD与AA1相交,AB与AD相交,
AA1与AB相交;A1D1与AA1相交,AB与AA1相交,
AB与A1D1异面.
3.如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是B1O和C1O的中点,则长方体的各棱中与EF平行的有( )
A.3条
B.4条
C.5条
D.6条
答案 B
解析 EF∥B1C1,EF∥BC,EF∥AD,EF∥A1D1.
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.2 空间两条直线的位置关系
第2课时 异面直线
课标阐释
1.借助长方体,通过直观感知,了解空间中直线与直线的位置关系.(几何直观)
2.掌握两异面直线所成的角的求法.(几何直观、数学运算)
思维脉络
【激趣诱思】
随着世界各国经济的发展和高速公路的出现,现代化的城市道路交通开始朝立体化发展.立体交叉桥,简称立交桥.世界上第一座立交桥是于1928年由美国建造的,此后世界各地的立交桥相继出现.1952年,我国于
北京滨河路兴建了首座立交桥.我国第二座立交桥是于1962年在广州修建的.现在的立交桥已由最初的上、下两层分开式,向多层次、多方向的复杂立体交叉方式发展,目的是大力提高交叉路口的车流速度,并确保交通安全.若把立交桥抽象成直线,它们在同一个平面内吗 这样的直线有何特征 一条南北走向和一条东西走向(不同层)的立交桥所在直线的夹角如何刻画
【知识梳理】
一、定理
过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
微练习
异面直线是指( )
A.空间中两条不相交的直线
B.分别位于两个不同平面内的两条直线
C.平面内的一条直线与平面外的一条直线
D.不同在任何一个平面内的两条直线
答案 D
解析 对于A,空间中两条不相交的直线有两种可能,一是平行(共面),另一个是异面.所以A应排除.对于B,分别位于两个不同平面内的两条直线,既可能平行也可能相交也可能异面,如图,就是相交的情况,所以B应排除.对于C,如图的a,b可看作是平面α内的一条直线a与平面α外的一条直线b,显然它们是相交直线,所以C应排除.D符合定义.
二、异面直线所成的角
(1)定义
如图,a与b是异面直线,经过空间任意一点O,作直线a'∥a,b'∥b,我们把直线a'和b'所成的锐角(或直角)叫作异面直线a,b所成的角或夹角.
(2)两条异面直线所成角的取值范围: .
(3)若异面直线a,b所成的角是直角,则称异面直线a,b互相垂直,记作a⊥b.
微判断
(1)异面直线所成的角的大小与O点的位置有关,即O点位置不同时,这一角的大小也不同.( )
(2)异面直线a与b所成角可以是0°.( )
(3)如果两条平行直线中的一条与某一条直线垂直,那么另一条直线也与这条直线垂直.( )
×
×
√
微练习
如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是 ;
(2)AC和D1C1所成的角是 ;
(3)AC和B1D1所成的角是 ;
(4)AC和A1B所成的角是 .
答案 (1)90° (2)45° (3)90° (4)60°
解析 (1)根据正方体的性质可得AC和DD1所成的角是90°.
(2)∵D1C1∥DC,∴∠ACD即为AC和D1C1所成的角,由正方体的性质得∠ACD=45°.
(3)∵BD∥B1D1,BD⊥AC,∴B1D1⊥AC,即AC和B1D1所成的角是90°.
(4)∵A1B∥D1C,△ACD1是等边三角形,∴AC和A1B所成的角是60°.
探究一
异面直线的判定
例1如图,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有 (填序号).
答案 ②④
解析 如题干图①中,GH∥MN.图②中,G,H,N三点共面,但M 平面GHN,因此直线GH与MN异面.图③中,连接GM,GM∥HN,因此,GH与MN共面.图④中,G,M,N三点共面,但H 平面GMN,因此GH与MN异面.所以图②,④中GH与MN异面.
技巧方法 判定两条直线是异面直线的方法
(1)证明两条直线既不平行又不相交.
(2)定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,B l,l α,则AB与l是异面直线(如图).
变式训练1(多选)
如图,E,F是AD上互异的两点,G,H是BC上互异的两点,由图可知,其中叙述正确的是( )
A.AB与CD互为异面直线
B.FH分别与DC,DB互为异面直线
C.EG与FH互为异面直线
D.EG与AB互为异面直线
答案 AC
解析 AB与平面BCD交于点B,且B CD,故AB与CD互为异面直线,故A正确.当H点落在C或F落在D点上时,FH与CD相交;当H落在B或F点落在D上时,FH与DB相交,故B错误.FH与平面EGD交于F点,而F EG,H 平面EGD,故EG与FH互为异面直线,故C正确.当G落在B上或E落在A上时,EG与AB相交,故D错误.所以A,C正确.
探究二
直线与直线垂直的证明
例2在直三棱柱ABC-A1B1C1中,AC⊥BC,求证:AC⊥BC1.
证明 如图,连接A1B,设A1C1=a,B1C1=b,AA1=h,因为三棱柱ABC-A1B1C1是直三棱柱,
所以∠BB1C1=∠A1AB=90°,
所以 =b2+h2,AB2=a2+b2,
A1B2=a2+b2+h2,
所以A1B2= ,
则A1C1⊥BC1,即∠A1C1B=90°.
又因为AC∥A1C1,所以∠A1C1B就是直线AC与BC1所成的角,所以AC⊥BC1.
技巧方法 证明空间的两条直线垂直的方法
(1)定义法:利用两条直线所成的角为90°证明两直线垂直.
(2)平面几何图形性质法:利用勾股定理、菱形的对角线相互垂直、等腰三角形(等边三角形)底边的中线和底边垂直等.
变式训练2如图,正方体ABCD-A1B1C1D1,求证:AC⊥B1D.
证明 如图,连接BD,交AC于O,设BB1的中点为E,
连接OE,则OE∥DB1,
所以OE与AC所成的角即为DB1与AC所成的角.
连接AE,CE,易证AE=CE,
又O是AC的中点,所以AC⊥OE,所以AC⊥B1D.
探究三
异面直线所成的角
角度1 求异面直线所成的角
例3在空间四边形ABCD中,AB=CD,且AB与CD所成锐角为30°,E,F分别为BC,AD的中点,求EF与AB所成角的大小.
解 如图所示,取AC的中点G,连接EG,FG,
则EG∥AB且EG= AB,GF∥CD且GF= CD.
由AB=CD知EG=FG,
从而可知∠GEF为EF与AB所成的角,
∠EGF或其补角为AB与CD所成的角.
∵AB与CD所成角为30°,∴∠EGF=30°或150°,
由EG=FG知△EFG为等腰三角形,当∠EGF=30°时,∠GEF=75°,当∠EGF=150°时,∠GEF=15°,
故EF与AB所成角的大小为15°或75°.
角度2 由异面直线所成角的大小求线段的长
例4如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2,求EF的长度.
解 取BC的中点M,连接ME,MF,如图.则ME∥AC,MF∥BD,
∴ME与MF所成的锐角(或直角)即为AC与BD所成的角,而AC,BD所成的角为60°,∴∠EMF=60°或∠EMF=120°.
规律总结 求两条异面直线所成的角的一般步骤
(1)构造角:根据异面直线的定义,通过作平行线或平移直线,作出异面直线夹角的相关角.
(2)计算角:求角度,常利用三角形.
(3)确定角:若求出的角是锐角或是直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
变式训练3如图所示,在正方体ABCD-A1B1C1D1中.
(1)求A1C1与B1C所成角的大小;
(2)若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.
解 (1)如图所示,连接AC,AB1.
由六面体ABCD-A1B1C1D1是正方体知,四边形AA1C1C为平行四边形,∴AC∥A1C1,从而B1C与AC所成的角就是A1C1与B1C所成的角.
在△AB1C中,由AB1=AC=B1C,可知∠B1CA=60°,
即A1C1与B1C所成的角为60°.
(2)如图所示,连接BD.由(1)知AC∥A1C1,
∴AC与EF所成的角就是A1C1与EF所成的角.
∵EF是△ABD的中位线,∴EF∥BD.
又AC⊥BD,∴AC⊥EF,∴EF⊥A1C1,
即A1C1与EF所成的角为90°.
素养形成
一题多解——异面直线的夹角问题
典例 如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
分析要求异面直线所成角的大小,关键是作出异面直线所成的角,把它归结到三角形中,通过解三角形就可以得出答案.同时在解题时要注意异面直线所成角的范围.
解法一(直接平移法)如图所示.
连接A1C1,B1D1交于点O,取DD1的中点G,连接GA1,GC1,OG,则OG∥B1D,EF∥A1C1,故∠GOA1或其补角就是异面直线DB1与EF所成的角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
解法二(中位线平移法)如图所示.
解法三如图所示,分别取AA1,CC1的中点M,N,连接MN,
则MN∥EF,所以直线MN与DB1所成的角就是异面直线DB1与EF所成的角.
连接MB1,DN,DM,B1N,则B1N∥DM,且B1N=DM,
∴四边形DMB1N为平行四边形,
∴MN与B1D必相交,设交点为P.
∴DM2=DP2+MP2,
∴∠DPM=90°,即DB1⊥EF,
∴异面直线DB1与EF所成的角为90°.
解法四(补形法)
如图所示,在原正方体的右侧补上一个同样的正方体,连接B1Q,DQ,则B1Q∥EF.
于是∠DB1Q或其补角就是异面直线DB1与EF所成的角,通过计算,不难得到B1D2+B1Q2=DQ2,故异面直线DB1与EF所成的角为90°.
反思感悟 (1)求两异面直线所成的角的三个步骤
①作:根据所成角的定义,用平移法作出异面直线所成的角;
②证:证明作出的角就是要求的角;
③计算:求角的值,常利用解三角形得出.
可用“一作二证三计算”来概括.注意异面直线所成角范围是0°<θ≤90°.
(2)求异面直线所成的角,关键是找出异面直线所成的角,这就需要借助于几何图形,探索和论述某角是异面直线所成的角.“找角”的方法可以利用直接平移法,也可以通过补体法,最后归结为三角形中计算角度;若夹角是直角,除了计算出直角,还可以用后面的证明垂直加以解决.本例充分体现了逻辑推理与数学运算的数学核心素养及化归数学思想的应用.
谢谢观看
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
