13.1 基本立体图形 课件(共87张PPT)2023-2024学年高中数学苏教版必修第二册
文档属性
| 名称 | 13.1 基本立体图形 课件(共87张PPT)2023-2024学年高中数学苏教版必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:55:06 | ||
图片预览






文档简介
(共87张PPT)
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.1 棱柱、棱锥和棱台
课标阐释
1.利用实物、计算机软件等观察空间图形,认识棱柱、棱锥、棱台的结构特征.(几何直观)
2.能运用这些特征描述现实生活中简单物体的结构.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
金字塔是一种方底、尖顶的石砌建筑物,是古代埃及埋葬国王、王后或王室其他成员的陵墓.它既不是金子做的,也不是我们通常所见的宝塔形.由于它规模宏大,从四面看都呈等腰三角形,很像汉语中的“金”字,故中文形象地把它译为“金字塔”.
在四千多年前,生产工具落后,埃及人是怎样采集并搬运数量如此之多、每块又如此之重的巨石,垒成如此宏伟的大金字塔的呢 这真是一个十分难解的谜.
一、棱柱、棱锥、棱台的结构特征
多面体 定义 图形及表示 相关概念 分类 特点
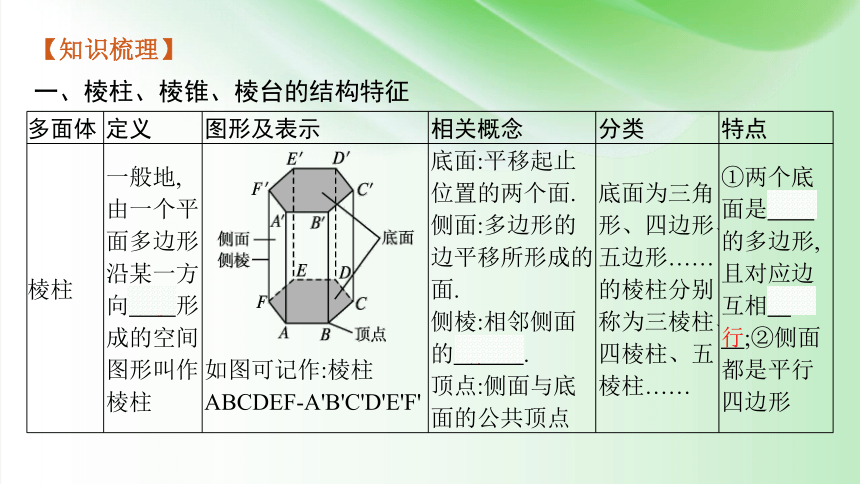
棱柱 一般地,由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱 如图可记作:棱柱ABCDEF-A'B'C'D'E'F' 底面:平移起止位置的两个面. 侧面:多边形的边平移所形成的面. 侧棱:相邻侧面的公共边. 顶点:侧面与底面的公共顶点 底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱…… ①两个底面是全等的多边形,且对应边互相平行;②侧面都是平行四边形
【知识梳理】
多面体 定义 图形及表示 相关概念 分类 特点
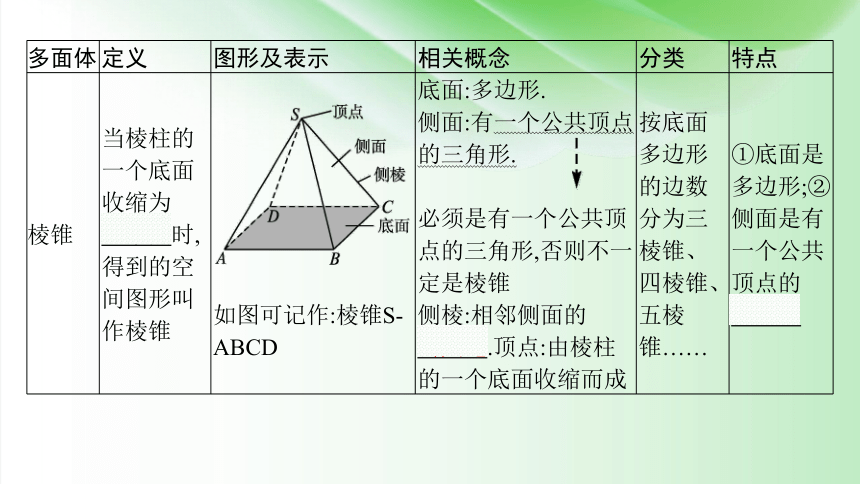
棱锥 当棱柱的一个底面收缩为 一个点时,得到的空间图形叫作棱锥 如图可记作:棱锥S-ABCD 底面:多边形. 侧面:有一个公共顶点的三角形. 必须是有一个公共顶点的三角形,否则不一定是棱锥 侧棱:相邻侧面的 公共边.顶点:由棱柱的一个底面收缩而成 按底面多边形的边数分为三棱锥、四棱锥、五棱锥…… ①底面是多边形;②侧面是有一个公共顶点的
三角形
多面体 定义 图形及表示 相关概念 分类 特点
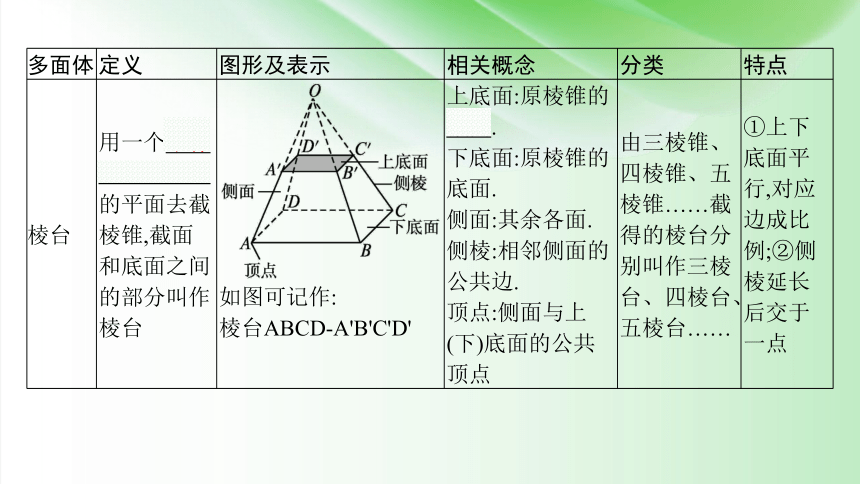
棱台 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分叫作棱台 如图可记作: 棱台ABCD-A'B'C'D' 上底面:原棱锥的截面. 下底面:原棱锥的底面. 侧面:其余各面. 侧棱:相邻侧面的公共边. 顶点:侧面与上 (下)底面的公共顶点 由三棱锥、四棱锥、五棱锥……截得的棱台分别叫作三棱台、四棱台、五棱台…… ①上下底面平行,对应边成比例;②侧棱延长后交于一点
名师点析 1.棱柱的结构特征包括两个方面:一是面,二是棱.棱柱的面共有两种:第一种是底面,上、下共两个底面而且是平行且全等的;第二种是侧面,几棱柱就有几个侧面,相邻侧面的公共边即侧棱都是平行的.它的棱也有两种,一种是侧棱,另一种就是底面上的边.
2.有一个面是多边形,其余各面是三角形的几何体不一定是棱锥,反例如右图所示.
3.(1)棱台上、下底面互相平行,且是两个相似的多边形,
它们的面积之比等于截去的小棱锥的高与原棱锥的高的比的平方.
(2)棱台的侧面均为梯形.
(3)棱台各侧棱延长线交于一点,棱台问题可还原为棱锥问题解决.
微判断
(1)棱柱的底面互相平行.( )
(2)棱柱的各个侧面都是平行四边形.( )
(3)长方体是四棱柱.( )
√
√
√
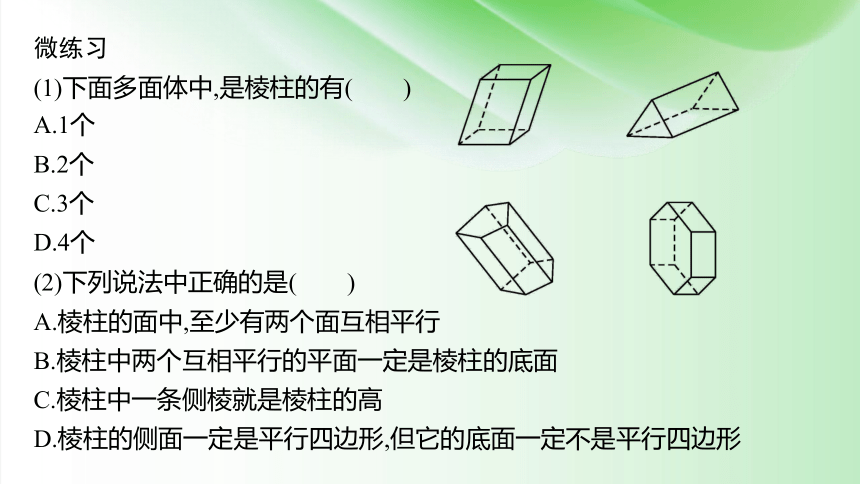
微练习
(1)下面多面体中,是棱柱的有( )
A.1个
B.2个
C.3个
D.4个
(2)下列说法中正确的是( )
A.棱柱的面中,至少有两个面互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中一条侧棱就是棱柱的高
D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形
答案 (1)D (2)A
解析 (1)根据棱柱的定义进行判断知,这4个图都满足.
(2)棱柱的两底面互相平行,故A正确;棱柱的侧面也可能有平行的面(如正方体),故B错;立在一起的一摞书可以看成一个四棱柱,当把这摞书推倾斜时,它的侧棱就不是棱柱的高了,故C错;由棱柱的定义知,棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错.
微思考
把棱台的各侧棱延长,交于一点吗
提示 因为棱台是由棱锥截得的,所以棱台中各侧棱延长后必相交于一点,否则不是棱台.
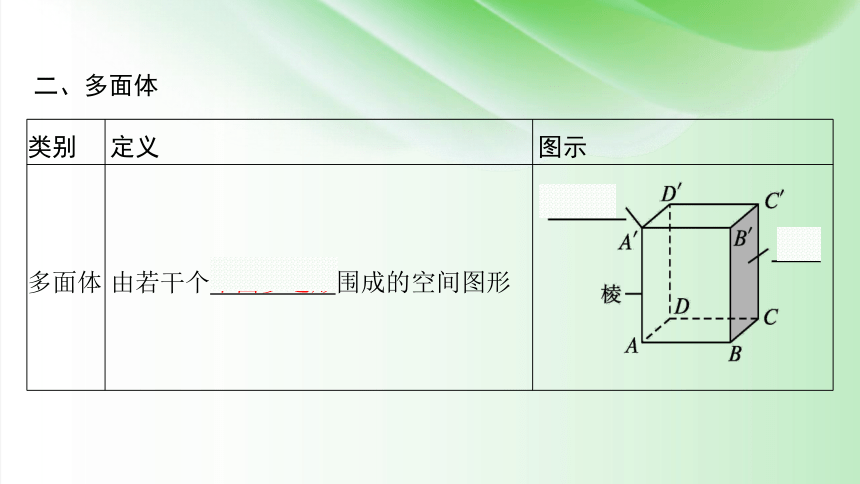
二、多面体
类别 定义 图示
多面体 由若干个平面多边形围成的空间图形
微思考
面数最少的多面体是什么
提示 围成一个多面体至少要四个面,所以面数最少的多面体是四面体,如三棱锥就是四面体.
探究一
棱柱的结构特征
例1下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
答案 D
解析 选项A,B都不正确,反例如图所示.选项C也不正确,上、下底面是全等的菱形,各侧面是全等的正方形的四棱柱不是正方体.根据棱柱的定义知选项D正确.
反思感悟 棱柱结构特征的辨析方法
(1)扣定义:判定一个几何体是否为棱柱的关键是棱柱的定义.
①看“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是平行四边形;
②看“线”,即观察每相邻两个四边形的公共边是否平行.
(2)举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.
变式训练1下列说法中,正确的是( )
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫作棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
答案 D
解析 A选项不符合棱柱的侧棱平行的特点;对于B选项,反例如图①所示;选项C中,反例如图②,底面ABCD可以是平行四边形;D选项说明了棱柱的特点,故选D.
探究二
棱锥、棱台的结构特征
例2(1)下列三种叙述,正确的有( )
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个 B.1个 C.2个 D.3个
(2)下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;②四面体的任何一个面都可以作为棱锥的底面;③棱锥的侧棱平行.
A.① B.①② C.② D.③
答案 (1)A (2)B
解析 (1)①中的平面不一定平行于棱锥底面,故①错误;②③可用反例去检验,如图所示,侧棱延长线不能相交于一点,故②③错.故选A.
(2)由棱锥的定义,知棱锥的各侧面都是三角形,故①正确;四面体就是由四个三角形所围成的几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故②正确;棱锥的侧棱交于一点,故③错误.
技巧方法 判断棱锥、棱台形状的两个方法
(1)举反例法:
结合棱锥、棱台的定义,举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法:
技巧 棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
变式训练2下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;②由四个平面围成的封闭图形只能是三棱锥;③棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是 .
答案 ①②
解析 ①
正确,棱台的侧面一定是梯形,而不是平行四边形;②正确,由四个平面围成的封闭图形只能是三棱锥;③错误,如图所示四棱锥被平面截成的两部分都是棱锥.
探究三
多面体表面距离最短问题
例3如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
分析把三棱锥的侧面展开,当△AEF的各边在同一直线上时,其周长最小.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,
∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4 ,
∴△AEF周长的最小值为4 .
要点笔记 本题是多面体表面上两点间的最短距离问题,常常要归结为求平面上两点间的最短距离问题.解决此类问题的方法就是先把多面体侧面展开,再用平面几何的知识来求解.
变式训练3如图,在以O为顶点的三棱锥中,过点O的三条棱,任意两条棱的夹角都是30°,在一条棱上有A,B两点,OA=4,OB=3,以A,B为端点用一条绳子紧绕三棱锥的侧面一周,求此绳在A,B之间的最短绳长.
解 作出三棱锥的侧面展开图,如图.A,B两点之间的最短绳长就是线段AB的长度.OA=4,OB=3,∠AOB=90°,所以AB=5,即此绳在A,B之间最短的绳长为5.
素养形成
几何体的平面展开图
典例 (1)请画出如图所示的正方体的平面展开图.
(2)如图是两个几何体的平面展开图,请问各是什么几何体
解 (1)展开图如图所示.(答案不唯一)
(2)根据平面展开图,可知①为五棱柱,②为三棱台.
方法点睛 (1)绘制展开图:绘制多面体的平面展开图要结合多面体的几何特征,发挥空间想象能力或者是亲手制作多面体模型.在解题过程中,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面,便可得到其平面展开图.
(2)由展开图复原几何体:若是给出多面体的平面展开图,来判断是由哪一个多面体展开的,则可把上述过程逆推.同一个几何体的平面展开图可能是不一样的,也就是说,一个多面体可有多个平面展开图.
变式训练如图所示,不是正四面体(各棱长都相等的三棱锥)的展开图的是( )
A.①③ B.②④ C.③④ D.①②
答案 C
解析 可选择阴影三角形作为底面进行折叠,发现①②可折成正四面体,③④折叠后只能围成无底的三棱锥.
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.2 圆柱、圆锥、圆台和球
课标阐释
1.理解圆柱、圆锥、圆台、球的定义,知道这四种几何体的结构特征,能够识别和区分这些几何体.(逻辑推理、直观想象)
2.了解柱体、锥体、台体之间的关系.(数学抽象)
3.了解简单组合体的概念和基本形式.(数学抽象)
4.会用柱、锥、台、球的结构特征描述简单组合体的结构特征.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
容器中的学问
油桶、热水瓶等都是用来装液体的容器,你有没有注意过装液体的容器大都是圆柱形的,这其中蕴含着怎样的数学方面的知识呢 事实上,装同样体积的液体的容器中,如果容器的高度一样,那么,做成圆柱形所需要的材料最省,因此油桶、热水瓶等容器大都是圆柱形的.
有没有比圆柱更省料的形状呢 有的.根据数学的原理,在同样材料做的一些容器中,球形容器的容积比圆柱形的更大.也就是说,做成球形容器,可以更节约材料.但是,球形容器很容易滚动,放不稳,它的盖子也不容易做,所以不实用.
放固体的容器,如盒子、箱子、柜子等,为什么不做成圆柱形的呢 虽然做成圆柱形的容器比较省料,但是用来装固体东西却不经济,所以通常把它们做成长方体形状.
【知识梳理】
一、圆柱、圆锥、圆台
将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、
垂直于底边的腰所在的直线旋转一周,形成的空间图形分别叫作圆柱、圆锥、圆台,这条直线叫作轴,垂直于轴的边旋转而成的圆面叫作底面,不垂直于轴的边旋转而成的曲面叫作侧面,无论旋转到什么位置,这条边都叫作母线(如图(1)(2)(3)所示),分别记作圆柱OO'、圆锥SO和圆台OO'.
名师点析 1.圆柱的性质
(1)圆柱的底面是两个半径相等的圆面,两圆面所在平面互相平行.
(2)通过轴的各个截面叫作轴截面,轴截面是全等的矩形.
(3)母线平行且相等,它们都垂直于底面,它们的长等于圆柱的高.
2.圆锥的性质
(1)圆锥的底面是一个圆面,圆面的半径就是直角边OA的长,底面和轴垂直.
(2)平行于底面的截面是圆面.
(3)通过轴的各个截面是轴截面,各轴截面是全等的等腰三角形,如△SAB.
(4)过顶点和底面相交的截面是等腰三角形,如等腰三角形SAC.
(5)母线都过顶点且相等,各母线与轴的夹角相等.
3.圆台的性质
(1)圆台的底面是两个半径不等的圆面,两圆面所在的平面互相平行又都和轴垂直.
(2)平行于底面的截面是圆面.
(3)通过轴的各个截面是轴截面,各轴截面是全等的等腰梯形,如梯形ABB1A1.
(4)任意两条母线确定的平面,截圆台所得的截面是等腰梯形,如梯形ACC1A.
(5)母线都相等,各母线延长后都相交于一点.
微判断
(1)圆锥有无数条母线,它们有公共点即圆锥的顶点,且长度相等.( )
(2)过圆锥的轴的截面是全等的等边三角形.( )
(3)圆台有无数条母线,且它们相等,但延长后不相交于一点.( )
(4)过圆台任意两条母线的截面是等腰梯形.( )
微思考
圆柱上底面圆周上任一点与下底面圆周上任一点的连线是圆柱的母线吗
提示 不一定.圆柱的母线与轴是平行的.
√
×
×
√
二、球面、球体
半圆绕着它的直径所在的直线旋转一周所形成的曲面叫作球面,球面围成的空间图形叫作球体,简称球,如图所示,记作球O.
球是一个几何体,包括表面及其内部
微思考
用一个平面去截球,得到的是一个圆吗
提示 不是,得到的是一个圆面.
微练习
(1)下列说法正确的是( )
A.圆锥的母线长等于底面圆直径 B.圆柱的母线与轴垂直
C.圆台的母线与轴平行 D.球的直径必过球心
(2)用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆台 C.球体 D.棱台
答案 (1)D (2)D
解析 (1)圆锥的母线长与底面直径无联系;圆柱的母线与轴平行;圆台的母线与轴不平行.
(2)圆柱、圆台和球体无论怎样截,不可能截出三角形.只有棱台可以截出三角形,故选D.
三、旋转面、旋转体
一般地,一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面叫作旋转面,封闭的旋转面围成的空间图形称为旋转体.圆柱、圆锥、圆台和球都是特殊的旋转体.
微思考
半圆或圆绕它的直径所在直线旋转一周形成什么
提示 半圆或圆绕它的直径所在直线旋转一周形成球面.
探究一
旋转体的结构特征
例1给出下列叙述:①圆柱的母线与它的轴可以不平行;②圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形;③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是( )
A.①② B.②③ C.①③ D.②④
答案 D
解析 由圆柱、圆锥、圆台的定义及母线的性质可知②④正确,①③错误.
要点笔记 (1)准确掌握圆柱、圆锥、圆台和球的生成过程及其特征性质是解决此类概念问题的关键.
(2)解题时要注意两个明确:
①明确由哪个平面图形旋转而成;
②明确旋转轴是哪条直线.
变式训练1下列说法正确的是 (填序号).
①以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
③圆柱、圆锥、圆台的底面都是圆;
④以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转180°形成的曲面围成的几何体是圆锥;
⑤球面上四个不同的点一定不在同一平面内;
⑥球的半径是球面上任意一点和球心的连线段.
答案 ④⑥
解析 ①以直角三角形的一条直角边所在直线为轴旋转一周才可以得到圆锥,故①错误;②以直角梯形垂直于底边的一腰所在直线为轴旋转一周才可以得到圆台,故②错误;③它们的底面为圆面,故③错误;④正确;作球的一个截面,在截面的圆周上任意取四个不同的点,则这四点就在球面上,故⑤错误;根据球的半径定义,知⑥正确.
探究二
组合体的结构特征
例2描述下列几何体的结构特征.
分析从简单组合体的两种基本构成形式入手分析.
解 图①所示的几何体是由两个圆台拼接而成的组合体;图②所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图③所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.
反思感悟 判断实物是由哪些简单几何体组成的技巧:
(1)准确理解简单几何体(柱、锥、台、球)的结构特征;
(2)正确掌握简单组合体构成的两种基本形式;
(3)若用分割的方法,则需要根据几何体的结构特征恰当地作出辅助线(或面).
变式训练2如图①②所示的图形绕虚线旋转一周后形成的立体图形分别是由哪些简单几何体组成的
解 旋转后的图形如图所示.其中图①是由一个圆柱O1O2和两个圆台O2O3,O4O3组成的;图②是由一个圆锥O5O4,一个圆柱O3O4及一个圆台O1O3中挖去圆锥O2O1组成的.
探究三
旋转体的有关计算
角度1 圆锥、圆台中的截面问题
例3圆台的两底面面积分别为1,49,平行于底面的截面的面积的2倍等于两底面面积之和,求圆台的高被截面分成的两部分的比.
解 将圆台还原为圆锥,如图所示.
O2,O1,O分别是圆台上底面、截面和下底面的圆心,
V是圆锥的顶点,
角度2 球中的截面问题
例4已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同侧,且距离等于1,求这个球的半径.
素养形成
转化与化归思想在求空间几何体表面上两点间最短距离中的应用
典例 如图,底面半径为1,高为2的圆柱,在点A处有一只蚂蚁,现在这只蚂蚁要围绕圆柱由点A爬到点B,问蚂蚁爬行的最短距离是多少
分析将圆柱的侧面沿母线剪开→侧面展开图→最短距离→计算求值
解 把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图,连接AB',则AB'即为蚂蚁爬行的最短距离.
方法点睛 求旋转体侧面上两点间的最短距离,一般转化为侧面展开图上两点间的距离进行求解.
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.3 直观图的斜二测画法
课标阐释
1.掌握斜二测画法的步骤.(数学抽象)
2.能用斜二测法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
皮影戏,旧称“影子戏”或“灯影戏”,是一种用灯光照射兽皮或纸板做成的人物剪影以表演故事的民间戏剧.表演时,艺人们在白色幕布后面,一边操纵戏曲人物,一边用当地流行的曲调唱述故事,同时配以打击乐器和弦乐,具有浓厚的乡土气息.千百年来,这门古老的艺术,伴随着祖祖辈辈的人们,度过了许多欢乐的时光.那么皮影戏中的这个“影”是什么投影 画几何体的直观图与皮影戏中形成的“影”原理一样吗
【知识梳理】
一、用斜二测画法画水平放置的平面图形的直观图的步骤
由于选轴的不同,画出的直观图可能不相同
微练习
(1)下列说法中正确的个数是( )
①水平放置的角的直观图一定是角;
②相等的角在直观图中仍然相等;
③相等的线段在直观图中仍然相等;
④若两条线段平行,则在直观图中对应的两条线段仍然平行.
A.1 B.2 C.3 D.4
(2)利用斜二测画法画出边长为3的正方形的直观图,正确的是图中的( )
答案 (1)B (2)C
解析 (1)①正确;②错误,如正方形的直观图为平行四边形,角度不一定相等;③错误,因为平行于x轴的线段长度不变,平行于y轴的线段长度变为原来的一半;④正确,平行性不会改变.
(2)正方形的直观图应是平行四边形,且相邻两边的边长之比为2∶1.
二、几何体直观图的画法规则
画几何体的直观图时,与画平面图形的直观图相比,只是多画一个与x轴、y轴都垂直的z轴,并且使平行于z轴的线段的平行性和长度都不变.
名师点析 画空间几何体的直观图的四个步骤
(1)画轴.通常以高所在直线为z轴建系.
(2)画底面.根据平面图形的直观图画法确定底面.
(3)画侧棱.利用与z轴平行或在z轴上的线段确定有关侧棱.
(4)连线成图.画图完成后,擦除辅助线,看得见的地方用实线,被遮挡的部分用虚线(或不画),就得到了几何体的直观图.
微练习
用斜二测画法画长、宽、高分别为2 cm、 cm、1 cm的长方体ABCD-A'B'C'D'的直观图.
画法 (1)画轴.如图,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
(2)画底面.以点O为中点,在x轴上取线段MN,使MN=2 cm;在y轴上取线段PQ,使PQ= cm.分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A,B,C,D,四边形ABCD就是长方体的底面ABCD.
(3)画侧棱.过A,B,C,D各点分别作z轴的平行线,并在这些平行线上分别截取1 cm长的线段AA',BB',CC',DD'.
(4)成图.顺次连接A',B',C',D',并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图.
探究一
画水平放置的平面图形的直观图
例1如图,画出水平放置的等腰梯形的直观图.
分析建系→定点→连线成图
画法 (1)如图①,取AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系,画对应的坐标系x'O'y',使∠x'O'y'=45°.
(2)在图②中,以点O'为中点在x'轴上取A'B'=AB,在y'轴上取O'E'= OE,以E'为中点画C'D'∥x'轴,并使C'D'=CD.
(3)连接B'C',D'A',并擦去辅助线x'轴和y'轴,所得的四边形A'B'C'D'就是水平放置的等腰梯形ABCD的直观图(如图③).
①
②
③
反思感悟 画水平放置的平面图形的直观图的技巧
(1)在画水平放置的平面图形的直观图时,选取适当的坐标系是关键,一般要使平面多边形尽可能多的顶点在坐标轴上,以便于画点.
(2)画平面图形的直观图,首先画与坐标轴平行的线段(平行性不变),与坐标轴不平行的线段通过与坐标轴平行的线段确定它的两个端点,然后连接成线段.
延伸探究 把本例图形换成右图,试画出该图的直观图.
画法 (1)在已知的直角梯形ABCD中,以底边AB所在直线为x轴,垂直于AB的腰AD所在直线为y轴建立平面直角坐标系.如图①.
(2)画相应的x'轴和y'轴,使∠x'O'y'=45°,在x'轴上取O'B'=AB,在y'轴上取O'D'= AD,过D'作x'轴的平行线l,在l上沿x'轴正方向取点C'使得D'C'=DC.如图②.
(3)连接B'C',所得四边形O'B'C'D'就是直角梯形ABCD的直观图.如图③.
探究二
画空间几何体的直观图
例2画出底面边长为1.2 cm的正方形,侧棱均相等,且高为1.5 cm的四棱锥的直观图.
画法(1)画轴.画x'轴、y'轴、z'轴,使∠x'O'y'=45°,∠x'O'z'=90°,如图①所示.
(2)画底面.以O'为中心在x'轴上截取线段EF,使EF=1.2 cm,在y'轴上截取线段GH,使GH=0.6 cm.
分别过E,F作y'轴的平行线,过G,H作x'轴的平行线,则交点分别为A,B,C,D,即四边形ABCD为底面正方形的直观图.
(3)画高.在z'轴上截取OP,使OP=1.5 cm.
(4)成图.顺次连接PA,PB,PC,PD,并擦去
辅助线,将被遮住的部分改为虚线,
得四棱锥的直观图,如图②所示.
反思感悟 1.画空间几何体的直观图时,一般是先按照画平面图形直观图的方法与步骤,画出其底面的直观图,再在z轴上确定该几何体的顶点或另一个底面的直观图所需坐标系的原点,从而作出另一个底面的直观图,最后得到整个几何体的直观图.
2.对于台体、柱体等有上底面的几何体,在作上底面的直观图时,可先作出高线,在上底面所在的平面内再建一个两轴分别与下底面中的坐标系中的两轴平行的坐标系,最后作出表示相应等量的线段并连接.
变式训练1用斜二测画法画出底面为正方形的四棱台的直观图,其中上、下底面边长分别为2,3,高为2.
画法(1)画轴.画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
(2)画下底面.以O为中心,在x轴上取线段MN,使MN=3,在y轴上取线段PQ,使PQ=1.5.分别过点M和点N作y轴的平行线,过点P和点Q作x轴的平行线,设它们的交点分别为A,B,C,D,则四边形ABCD即为四棱台的下底面.
(3)画上底面.在z轴上取一点O',使OO'=2,以O'为原点画直线a和直线b,使直线a∥x轴,直线b∥y轴,在平面aO'b内以O'为中心画水平放置的边长为2的正方形的直观图A'B'C'D'.
(4)连线.被遮挡的线画成虚线(如图①),
擦去辅助线并整理就得到四棱台的
直观图(如图②).
探究三
直观图的还原与计算
例3(1)在如图所示的直观图中,A'B'∥y'轴,B'C'∥A'D'∥x'轴,且B'C'≠A'D',则其对应的平面图形ABCD是( )
A.任意梯形 B.直角梯形
C.任意四边形 D.平行四边形
(2)已知等边三角形ABC的直观图△A'B'C‘
的面积为 ,则等边三角形ABC的面积是 .
答案 (1)B (2)
解析 (1)由直观图的画法,可知原四边形ABCD为直角梯形.
(2)按照斜二测画法的规则,把如图①所示的等边三角形ABC的直观图△A'B'C'还原为如图②所示的等边三角形ABC,
反思感悟 1.借助水平放置的平面图形的直观图还原成原来的实际图形,其作法就是逆用斜二测画法,也就是使平行于x'轴的线段的长度不变,而平行于y'轴的线段的长度变为原来的2倍,还原时要抓住关键点和关键线段.
2.平面多边形与其直观图面积间关系:一个平面多边形的面积为S原,斜二测画法得到直观图的面积为S直,则有S直= S原.
变式训练2(1)如图,矩形O'A'B'C'是水平放置的一个平面图形的直观图,其中O'A'=6 cm,O'C'=2 cm,C'D'=2 cm,则原图形是( )
A.正方形
B.矩形
C.菱形
D.一般的平行四边形
(2)如图是一个四边形的直观图,则其原图形的面积为 .
答案 (1)C (2)15
素养形成
易错辨析——考虑问题不全面致错
典例 已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,若平行四边形中有一条边长为4,则此正方形的面积是( )
A.16 B.36或64
C.16或64 D.36
答案 C
错解 正方形的边长在直观图中对应边长为4,则原图中正方形的边长为4,故原图形的面积为42=16.故选A.
正解 正方形的直观图是一个平行四边形,长度为4的边,可能为水平放置的边,也可能为竖直放置的一边,所以要分情况进行讨论.
若正方形的水平放置的边长在直观图中对应边长为4,则原图中正方形的边长为4,故原图形的面积为42=16;
若正方形的竖直放置的边长在直观图中对应边长为4,则原图中正方形的边长为8,故原图形的面积为82=64.
综上,选C.
纠错心得解决此类问题的关键在于准确把握斜二测画法规则,另外要注意边所在位置对直观图的影响,如果没有指明边所在的位置,就需要对其进行分类讨论.
谢谢观看
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.1 棱柱、棱锥和棱台
课标阐释
1.利用实物、计算机软件等观察空间图形,认识棱柱、棱锥、棱台的结构特征.(几何直观)
2.能运用这些特征描述现实生活中简单物体的结构.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
金字塔是一种方底、尖顶的石砌建筑物,是古代埃及埋葬国王、王后或王室其他成员的陵墓.它既不是金子做的,也不是我们通常所见的宝塔形.由于它规模宏大,从四面看都呈等腰三角形,很像汉语中的“金”字,故中文形象地把它译为“金字塔”.
在四千多年前,生产工具落后,埃及人是怎样采集并搬运数量如此之多、每块又如此之重的巨石,垒成如此宏伟的大金字塔的呢 这真是一个十分难解的谜.
一、棱柱、棱锥、棱台的结构特征
多面体 定义 图形及表示 相关概念 分类 特点
棱柱 一般地,由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱 如图可记作:棱柱ABCDEF-A'B'C'D'E'F' 底面:平移起止位置的两个面. 侧面:多边形的边平移所形成的面. 侧棱:相邻侧面的公共边. 顶点:侧面与底面的公共顶点 底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱…… ①两个底面是全等的多边形,且对应边互相平行;②侧面都是平行四边形
【知识梳理】
多面体 定义 图形及表示 相关概念 分类 特点
棱锥 当棱柱的一个底面收缩为 一个点时,得到的空间图形叫作棱锥 如图可记作:棱锥S-ABCD 底面:多边形. 侧面:有一个公共顶点的三角形. 必须是有一个公共顶点的三角形,否则不一定是棱锥 侧棱:相邻侧面的 公共边.顶点:由棱柱的一个底面收缩而成 按底面多边形的边数分为三棱锥、四棱锥、五棱锥…… ①底面是多边形;②侧面是有一个公共顶点的
三角形
多面体 定义 图形及表示 相关概念 分类 特点
棱台 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分叫作棱台 如图可记作: 棱台ABCD-A'B'C'D' 上底面:原棱锥的截面. 下底面:原棱锥的底面. 侧面:其余各面. 侧棱:相邻侧面的公共边. 顶点:侧面与上 (下)底面的公共顶点 由三棱锥、四棱锥、五棱锥……截得的棱台分别叫作三棱台、四棱台、五棱台…… ①上下底面平行,对应边成比例;②侧棱延长后交于一点
名师点析 1.棱柱的结构特征包括两个方面:一是面,二是棱.棱柱的面共有两种:第一种是底面,上、下共两个底面而且是平行且全等的;第二种是侧面,几棱柱就有几个侧面,相邻侧面的公共边即侧棱都是平行的.它的棱也有两种,一种是侧棱,另一种就是底面上的边.
2.有一个面是多边形,其余各面是三角形的几何体不一定是棱锥,反例如右图所示.
3.(1)棱台上、下底面互相平行,且是两个相似的多边形,
它们的面积之比等于截去的小棱锥的高与原棱锥的高的比的平方.
(2)棱台的侧面均为梯形.
(3)棱台各侧棱延长线交于一点,棱台问题可还原为棱锥问题解决.
微判断
(1)棱柱的底面互相平行.( )
(2)棱柱的各个侧面都是平行四边形.( )
(3)长方体是四棱柱.( )
√
√
√
微练习
(1)下面多面体中,是棱柱的有( )
A.1个
B.2个
C.3个
D.4个
(2)下列说法中正确的是( )
A.棱柱的面中,至少有两个面互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中一条侧棱就是棱柱的高
D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形
答案 (1)D (2)A
解析 (1)根据棱柱的定义进行判断知,这4个图都满足.
(2)棱柱的两底面互相平行,故A正确;棱柱的侧面也可能有平行的面(如正方体),故B错;立在一起的一摞书可以看成一个四棱柱,当把这摞书推倾斜时,它的侧棱就不是棱柱的高了,故C错;由棱柱的定义知,棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错.
微思考
把棱台的各侧棱延长,交于一点吗
提示 因为棱台是由棱锥截得的,所以棱台中各侧棱延长后必相交于一点,否则不是棱台.
二、多面体
类别 定义 图示
多面体 由若干个平面多边形围成的空间图形
微思考
面数最少的多面体是什么
提示 围成一个多面体至少要四个面,所以面数最少的多面体是四面体,如三棱锥就是四面体.
探究一
棱柱的结构特征
例1下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
答案 D
解析 选项A,B都不正确,反例如图所示.选项C也不正确,上、下底面是全等的菱形,各侧面是全等的正方形的四棱柱不是正方体.根据棱柱的定义知选项D正确.
反思感悟 棱柱结构特征的辨析方法
(1)扣定义:判定一个几何体是否为棱柱的关键是棱柱的定义.
①看“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是平行四边形;
②看“线”,即观察每相邻两个四边形的公共边是否平行.
(2)举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.
变式训练1下列说法中,正确的是( )
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫作棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
答案 D
解析 A选项不符合棱柱的侧棱平行的特点;对于B选项,反例如图①所示;选项C中,反例如图②,底面ABCD可以是平行四边形;D选项说明了棱柱的特点,故选D.
探究二
棱锥、棱台的结构特征
例2(1)下列三种叙述,正确的有( )
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个 B.1个 C.2个 D.3个
(2)下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;②四面体的任何一个面都可以作为棱锥的底面;③棱锥的侧棱平行.
A.① B.①② C.② D.③
答案 (1)A (2)B
解析 (1)①中的平面不一定平行于棱锥底面,故①错误;②③可用反例去检验,如图所示,侧棱延长线不能相交于一点,故②③错.故选A.
(2)由棱锥的定义,知棱锥的各侧面都是三角形,故①正确;四面体就是由四个三角形所围成的几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故②正确;棱锥的侧棱交于一点,故③错误.
技巧方法 判断棱锥、棱台形状的两个方法
(1)举反例法:
结合棱锥、棱台的定义,举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法:
技巧 棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
变式训练2下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;②由四个平面围成的封闭图形只能是三棱锥;③棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是 .
答案 ①②
解析 ①
正确,棱台的侧面一定是梯形,而不是平行四边形;②正确,由四个平面围成的封闭图形只能是三棱锥;③错误,如图所示四棱锥被平面截成的两部分都是棱锥.
探究三
多面体表面距离最短问题
例3如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
分析把三棱锥的侧面展开,当△AEF的各边在同一直线上时,其周长最小.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,
∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4 ,
∴△AEF周长的最小值为4 .
要点笔记 本题是多面体表面上两点间的最短距离问题,常常要归结为求平面上两点间的最短距离问题.解决此类问题的方法就是先把多面体侧面展开,再用平面几何的知识来求解.
变式训练3如图,在以O为顶点的三棱锥中,过点O的三条棱,任意两条棱的夹角都是30°,在一条棱上有A,B两点,OA=4,OB=3,以A,B为端点用一条绳子紧绕三棱锥的侧面一周,求此绳在A,B之间的最短绳长.
解 作出三棱锥的侧面展开图,如图.A,B两点之间的最短绳长就是线段AB的长度.OA=4,OB=3,∠AOB=90°,所以AB=5,即此绳在A,B之间最短的绳长为5.
素养形成
几何体的平面展开图
典例 (1)请画出如图所示的正方体的平面展开图.
(2)如图是两个几何体的平面展开图,请问各是什么几何体
解 (1)展开图如图所示.(答案不唯一)
(2)根据平面展开图,可知①为五棱柱,②为三棱台.
方法点睛 (1)绘制展开图:绘制多面体的平面展开图要结合多面体的几何特征,发挥空间想象能力或者是亲手制作多面体模型.在解题过程中,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面,便可得到其平面展开图.
(2)由展开图复原几何体:若是给出多面体的平面展开图,来判断是由哪一个多面体展开的,则可把上述过程逆推.同一个几何体的平面展开图可能是不一样的,也就是说,一个多面体可有多个平面展开图.
变式训练如图所示,不是正四面体(各棱长都相等的三棱锥)的展开图的是( )
A.①③ B.②④ C.③④ D.①②
答案 C
解析 可选择阴影三角形作为底面进行折叠,发现①②可折成正四面体,③④折叠后只能围成无底的三棱锥.
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.2 圆柱、圆锥、圆台和球
课标阐释
1.理解圆柱、圆锥、圆台、球的定义,知道这四种几何体的结构特征,能够识别和区分这些几何体.(逻辑推理、直观想象)
2.了解柱体、锥体、台体之间的关系.(数学抽象)
3.了解简单组合体的概念和基本形式.(数学抽象)
4.会用柱、锥、台、球的结构特征描述简单组合体的结构特征.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
容器中的学问
油桶、热水瓶等都是用来装液体的容器,你有没有注意过装液体的容器大都是圆柱形的,这其中蕴含着怎样的数学方面的知识呢 事实上,装同样体积的液体的容器中,如果容器的高度一样,那么,做成圆柱形所需要的材料最省,因此油桶、热水瓶等容器大都是圆柱形的.
有没有比圆柱更省料的形状呢 有的.根据数学的原理,在同样材料做的一些容器中,球形容器的容积比圆柱形的更大.也就是说,做成球形容器,可以更节约材料.但是,球形容器很容易滚动,放不稳,它的盖子也不容易做,所以不实用.
放固体的容器,如盒子、箱子、柜子等,为什么不做成圆柱形的呢 虽然做成圆柱形的容器比较省料,但是用来装固体东西却不经济,所以通常把它们做成长方体形状.
【知识梳理】
一、圆柱、圆锥、圆台
将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、
垂直于底边的腰所在的直线旋转一周,形成的空间图形分别叫作圆柱、圆锥、圆台,这条直线叫作轴,垂直于轴的边旋转而成的圆面叫作底面,不垂直于轴的边旋转而成的曲面叫作侧面,无论旋转到什么位置,这条边都叫作母线(如图(1)(2)(3)所示),分别记作圆柱OO'、圆锥SO和圆台OO'.
名师点析 1.圆柱的性质
(1)圆柱的底面是两个半径相等的圆面,两圆面所在平面互相平行.
(2)通过轴的各个截面叫作轴截面,轴截面是全等的矩形.
(3)母线平行且相等,它们都垂直于底面,它们的长等于圆柱的高.
2.圆锥的性质
(1)圆锥的底面是一个圆面,圆面的半径就是直角边OA的长,底面和轴垂直.
(2)平行于底面的截面是圆面.
(3)通过轴的各个截面是轴截面,各轴截面是全等的等腰三角形,如△SAB.
(4)过顶点和底面相交的截面是等腰三角形,如等腰三角形SAC.
(5)母线都过顶点且相等,各母线与轴的夹角相等.
3.圆台的性质
(1)圆台的底面是两个半径不等的圆面,两圆面所在的平面互相平行又都和轴垂直.
(2)平行于底面的截面是圆面.
(3)通过轴的各个截面是轴截面,各轴截面是全等的等腰梯形,如梯形ABB1A1.
(4)任意两条母线确定的平面,截圆台所得的截面是等腰梯形,如梯形ACC1A.
(5)母线都相等,各母线延长后都相交于一点.
微判断
(1)圆锥有无数条母线,它们有公共点即圆锥的顶点,且长度相等.( )
(2)过圆锥的轴的截面是全等的等边三角形.( )
(3)圆台有无数条母线,且它们相等,但延长后不相交于一点.( )
(4)过圆台任意两条母线的截面是等腰梯形.( )
微思考
圆柱上底面圆周上任一点与下底面圆周上任一点的连线是圆柱的母线吗
提示 不一定.圆柱的母线与轴是平行的.
√
×
×
√
二、球面、球体
半圆绕着它的直径所在的直线旋转一周所形成的曲面叫作球面,球面围成的空间图形叫作球体,简称球,如图所示,记作球O.
球是一个几何体,包括表面及其内部
微思考
用一个平面去截球,得到的是一个圆吗
提示 不是,得到的是一个圆面.
微练习
(1)下列说法正确的是( )
A.圆锥的母线长等于底面圆直径 B.圆柱的母线与轴垂直
C.圆台的母线与轴平行 D.球的直径必过球心
(2)用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
A.圆柱 B.圆台 C.球体 D.棱台
答案 (1)D (2)D
解析 (1)圆锥的母线长与底面直径无联系;圆柱的母线与轴平行;圆台的母线与轴不平行.
(2)圆柱、圆台和球体无论怎样截,不可能截出三角形.只有棱台可以截出三角形,故选D.
三、旋转面、旋转体
一般地,一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面叫作旋转面,封闭的旋转面围成的空间图形称为旋转体.圆柱、圆锥、圆台和球都是特殊的旋转体.
微思考
半圆或圆绕它的直径所在直线旋转一周形成什么
提示 半圆或圆绕它的直径所在直线旋转一周形成球面.
探究一
旋转体的结构特征
例1给出下列叙述:①圆柱的母线与它的轴可以不平行;②圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形;③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是( )
A.①② B.②③ C.①③ D.②④
答案 D
解析 由圆柱、圆锥、圆台的定义及母线的性质可知②④正确,①③错误.
要点笔记 (1)准确掌握圆柱、圆锥、圆台和球的生成过程及其特征性质是解决此类概念问题的关键.
(2)解题时要注意两个明确:
①明确由哪个平面图形旋转而成;
②明确旋转轴是哪条直线.
变式训练1下列说法正确的是 (填序号).
①以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
③圆柱、圆锥、圆台的底面都是圆;
④以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转180°形成的曲面围成的几何体是圆锥;
⑤球面上四个不同的点一定不在同一平面内;
⑥球的半径是球面上任意一点和球心的连线段.
答案 ④⑥
解析 ①以直角三角形的一条直角边所在直线为轴旋转一周才可以得到圆锥,故①错误;②以直角梯形垂直于底边的一腰所在直线为轴旋转一周才可以得到圆台,故②错误;③它们的底面为圆面,故③错误;④正确;作球的一个截面,在截面的圆周上任意取四个不同的点,则这四点就在球面上,故⑤错误;根据球的半径定义,知⑥正确.
探究二
组合体的结构特征
例2描述下列几何体的结构特征.
分析从简单组合体的两种基本构成形式入手分析.
解 图①所示的几何体是由两个圆台拼接而成的组合体;图②所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图③所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.
反思感悟 判断实物是由哪些简单几何体组成的技巧:
(1)准确理解简单几何体(柱、锥、台、球)的结构特征;
(2)正确掌握简单组合体构成的两种基本形式;
(3)若用分割的方法,则需要根据几何体的结构特征恰当地作出辅助线(或面).
变式训练2如图①②所示的图形绕虚线旋转一周后形成的立体图形分别是由哪些简单几何体组成的
解 旋转后的图形如图所示.其中图①是由一个圆柱O1O2和两个圆台O2O3,O4O3组成的;图②是由一个圆锥O5O4,一个圆柱O3O4及一个圆台O1O3中挖去圆锥O2O1组成的.
探究三
旋转体的有关计算
角度1 圆锥、圆台中的截面问题
例3圆台的两底面面积分别为1,49,平行于底面的截面的面积的2倍等于两底面面积之和,求圆台的高被截面分成的两部分的比.
解 将圆台还原为圆锥,如图所示.
O2,O1,O分别是圆台上底面、截面和下底面的圆心,
V是圆锥的顶点,
角度2 球中的截面问题
例4已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同侧,且距离等于1,求这个球的半径.
素养形成
转化与化归思想在求空间几何体表面上两点间最短距离中的应用
典例 如图,底面半径为1,高为2的圆柱,在点A处有一只蚂蚁,现在这只蚂蚁要围绕圆柱由点A爬到点B,问蚂蚁爬行的最短距离是多少
分析将圆柱的侧面沿母线剪开→侧面展开图→最短距离→计算求值
解 把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图,连接AB',则AB'即为蚂蚁爬行的最短距离.
方法点睛 求旋转体侧面上两点间的最短距离,一般转化为侧面展开图上两点间的距离进行求解.
高中数学苏教版必修第二册
第13章 立体几何初步
13.1 基本立体图形
13.1.3 直观图的斜二测画法
课标阐释
1.掌握斜二测画法的步骤.(数学抽象)
2.能用斜二测法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
皮影戏,旧称“影子戏”或“灯影戏”,是一种用灯光照射兽皮或纸板做成的人物剪影以表演故事的民间戏剧.表演时,艺人们在白色幕布后面,一边操纵戏曲人物,一边用当地流行的曲调唱述故事,同时配以打击乐器和弦乐,具有浓厚的乡土气息.千百年来,这门古老的艺术,伴随着祖祖辈辈的人们,度过了许多欢乐的时光.那么皮影戏中的这个“影”是什么投影 画几何体的直观图与皮影戏中形成的“影”原理一样吗
【知识梳理】
一、用斜二测画法画水平放置的平面图形的直观图的步骤
由于选轴的不同,画出的直观图可能不相同
微练习
(1)下列说法中正确的个数是( )
①水平放置的角的直观图一定是角;
②相等的角在直观图中仍然相等;
③相等的线段在直观图中仍然相等;
④若两条线段平行,则在直观图中对应的两条线段仍然平行.
A.1 B.2 C.3 D.4
(2)利用斜二测画法画出边长为3的正方形的直观图,正确的是图中的( )
答案 (1)B (2)C
解析 (1)①正确;②错误,如正方形的直观图为平行四边形,角度不一定相等;③错误,因为平行于x轴的线段长度不变,平行于y轴的线段长度变为原来的一半;④正确,平行性不会改变.
(2)正方形的直观图应是平行四边形,且相邻两边的边长之比为2∶1.
二、几何体直观图的画法规则
画几何体的直观图时,与画平面图形的直观图相比,只是多画一个与x轴、y轴都垂直的z轴,并且使平行于z轴的线段的平行性和长度都不变.
名师点析 画空间几何体的直观图的四个步骤
(1)画轴.通常以高所在直线为z轴建系.
(2)画底面.根据平面图形的直观图画法确定底面.
(3)画侧棱.利用与z轴平行或在z轴上的线段确定有关侧棱.
(4)连线成图.画图完成后,擦除辅助线,看得见的地方用实线,被遮挡的部分用虚线(或不画),就得到了几何体的直观图.
微练习
用斜二测画法画长、宽、高分别为2 cm、 cm、1 cm的长方体ABCD-A'B'C'D'的直观图.
画法 (1)画轴.如图,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
(2)画底面.以点O为中点,在x轴上取线段MN,使MN=2 cm;在y轴上取线段PQ,使PQ= cm.分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A,B,C,D,四边形ABCD就是长方体的底面ABCD.
(3)画侧棱.过A,B,C,D各点分别作z轴的平行线,并在这些平行线上分别截取1 cm长的线段AA',BB',CC',DD'.
(4)成图.顺次连接A',B',C',D',并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图.
探究一
画水平放置的平面图形的直观图
例1如图,画出水平放置的等腰梯形的直观图.
分析建系→定点→连线成图
画法 (1)如图①,取AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系,画对应的坐标系x'O'y',使∠x'O'y'=45°.
(2)在图②中,以点O'为中点在x'轴上取A'B'=AB,在y'轴上取O'E'= OE,以E'为中点画C'D'∥x'轴,并使C'D'=CD.
(3)连接B'C',D'A',并擦去辅助线x'轴和y'轴,所得的四边形A'B'C'D'就是水平放置的等腰梯形ABCD的直观图(如图③).
①
②
③
反思感悟 画水平放置的平面图形的直观图的技巧
(1)在画水平放置的平面图形的直观图时,选取适当的坐标系是关键,一般要使平面多边形尽可能多的顶点在坐标轴上,以便于画点.
(2)画平面图形的直观图,首先画与坐标轴平行的线段(平行性不变),与坐标轴不平行的线段通过与坐标轴平行的线段确定它的两个端点,然后连接成线段.
延伸探究 把本例图形换成右图,试画出该图的直观图.
画法 (1)在已知的直角梯形ABCD中,以底边AB所在直线为x轴,垂直于AB的腰AD所在直线为y轴建立平面直角坐标系.如图①.
(2)画相应的x'轴和y'轴,使∠x'O'y'=45°,在x'轴上取O'B'=AB,在y'轴上取O'D'= AD,过D'作x'轴的平行线l,在l上沿x'轴正方向取点C'使得D'C'=DC.如图②.
(3)连接B'C',所得四边形O'B'C'D'就是直角梯形ABCD的直观图.如图③.
探究二
画空间几何体的直观图
例2画出底面边长为1.2 cm的正方形,侧棱均相等,且高为1.5 cm的四棱锥的直观图.
画法(1)画轴.画x'轴、y'轴、z'轴,使∠x'O'y'=45°,∠x'O'z'=90°,如图①所示.
(2)画底面.以O'为中心在x'轴上截取线段EF,使EF=1.2 cm,在y'轴上截取线段GH,使GH=0.6 cm.
分别过E,F作y'轴的平行线,过G,H作x'轴的平行线,则交点分别为A,B,C,D,即四边形ABCD为底面正方形的直观图.
(3)画高.在z'轴上截取OP,使OP=1.5 cm.
(4)成图.顺次连接PA,PB,PC,PD,并擦去
辅助线,将被遮住的部分改为虚线,
得四棱锥的直观图,如图②所示.
反思感悟 1.画空间几何体的直观图时,一般是先按照画平面图形直观图的方法与步骤,画出其底面的直观图,再在z轴上确定该几何体的顶点或另一个底面的直观图所需坐标系的原点,从而作出另一个底面的直观图,最后得到整个几何体的直观图.
2.对于台体、柱体等有上底面的几何体,在作上底面的直观图时,可先作出高线,在上底面所在的平面内再建一个两轴分别与下底面中的坐标系中的两轴平行的坐标系,最后作出表示相应等量的线段并连接.
变式训练1用斜二测画法画出底面为正方形的四棱台的直观图,其中上、下底面边长分别为2,3,高为2.
画法(1)画轴.画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
(2)画下底面.以O为中心,在x轴上取线段MN,使MN=3,在y轴上取线段PQ,使PQ=1.5.分别过点M和点N作y轴的平行线,过点P和点Q作x轴的平行线,设它们的交点分别为A,B,C,D,则四边形ABCD即为四棱台的下底面.
(3)画上底面.在z轴上取一点O',使OO'=2,以O'为原点画直线a和直线b,使直线a∥x轴,直线b∥y轴,在平面aO'b内以O'为中心画水平放置的边长为2的正方形的直观图A'B'C'D'.
(4)连线.被遮挡的线画成虚线(如图①),
擦去辅助线并整理就得到四棱台的
直观图(如图②).
探究三
直观图的还原与计算
例3(1)在如图所示的直观图中,A'B'∥y'轴,B'C'∥A'D'∥x'轴,且B'C'≠A'D',则其对应的平面图形ABCD是( )
A.任意梯形 B.直角梯形
C.任意四边形 D.平行四边形
(2)已知等边三角形ABC的直观图△A'B'C‘
的面积为 ,则等边三角形ABC的面积是 .
答案 (1)B (2)
解析 (1)由直观图的画法,可知原四边形ABCD为直角梯形.
(2)按照斜二测画法的规则,把如图①所示的等边三角形ABC的直观图△A'B'C'还原为如图②所示的等边三角形ABC,
反思感悟 1.借助水平放置的平面图形的直观图还原成原来的实际图形,其作法就是逆用斜二测画法,也就是使平行于x'轴的线段的长度不变,而平行于y'轴的线段的长度变为原来的2倍,还原时要抓住关键点和关键线段.
2.平面多边形与其直观图面积间关系:一个平面多边形的面积为S原,斜二测画法得到直观图的面积为S直,则有S直= S原.
变式训练2(1)如图,矩形O'A'B'C'是水平放置的一个平面图形的直观图,其中O'A'=6 cm,O'C'=2 cm,C'D'=2 cm,则原图形是( )
A.正方形
B.矩形
C.菱形
D.一般的平行四边形
(2)如图是一个四边形的直观图,则其原图形的面积为 .
答案 (1)C (2)15
素养形成
易错辨析——考虑问题不全面致错
典例 已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,若平行四边形中有一条边长为4,则此正方形的面积是( )
A.16 B.36或64
C.16或64 D.36
答案 C
错解 正方形的边长在直观图中对应边长为4,则原图中正方形的边长为4,故原图形的面积为42=16.故选A.
正解 正方形的直观图是一个平行四边形,长度为4的边,可能为水平放置的边,也可能为竖直放置的一边,所以要分情况进行讨论.
若正方形的水平放置的边长在直观图中对应边长为4,则原图中正方形的边长为4,故原图形的面积为42=16;
若正方形的竖直放置的边长在直观图中对应边长为4,则原图中正方形的边长为8,故原图形的面积为82=64.
综上,选C.
纠错心得解决此类问题的关键在于准确把握斜二测画法规则,另外要注意边所在位置对直观图的影响,如果没有指明边所在的位置,就需要对其进行分类讨论.
谢谢观看
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
