13.2.4 平面与平面的位置关系 课件(共65张PPT)2023-2024学年高中数学苏教版必修第二册
文档属性
| 名称 | 13.2.4 平面与平面的位置关系 课件(共65张PPT)2023-2024学年高中数学苏教版必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:53:28 | ||
图片预览








文档简介
(共65张PPT)
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.4 平面与平面的位置关系
第1课时 两平面平行
课标阐释
1.理解并掌握平面与平面平行的判定定理.(数学抽象)
2.理解并掌握平面与平面平行的性质定理.(数学抽象)
3.能够应用平面与平面平行的判定定理和性质定理证明相关问题.(直观想象、逻辑推理)
4.了解两个平行平面间的距离的概念.(数学抽象)
思维脉络
【激趣诱思】
《老子》中说:“上善若水,水善利万物而不争.”一滴水,可方可圆,泽润万物;一个人,能方能圆,方圆相济,便可活得豁达、圆满.“方中有圆,圆中有方”是大自然的规律,也是为人处世的准则.“天行健,君子以自强不息;地势坤,君子以厚德载物.”在这里,圆是天地周而复始运转不息的象征,方是大地之旷远宽厚稳重的象征.我国古代的钱币,外部是圆形,内部是方孔,看似朴实无华,但蕴含着古人智慧和人生哲理.我们学习过的旋转体圆柱就蕴含着长方形的截面,它是如何得到的 能否用数学原理解释截面的形状
【知识梳理】
一、平面平行和平面相交的定义
1.两个平面互相平行的定义:如果两个平面没有公共点,那么称这两个平面互相平行.
2.两个平面相交的定义:如果两个平面有一个公共点,那么由基本事实3可知,它们相交于经过这个点的一条直线,此时称这两个平面相交.
微思考
两个平面平行,那么两个平面内的所有直线都相互平行吗
提示 不一定.因为两个平面平行,所以分别在这两个平面内的任意两条直线无公共点,它们平行或异面.
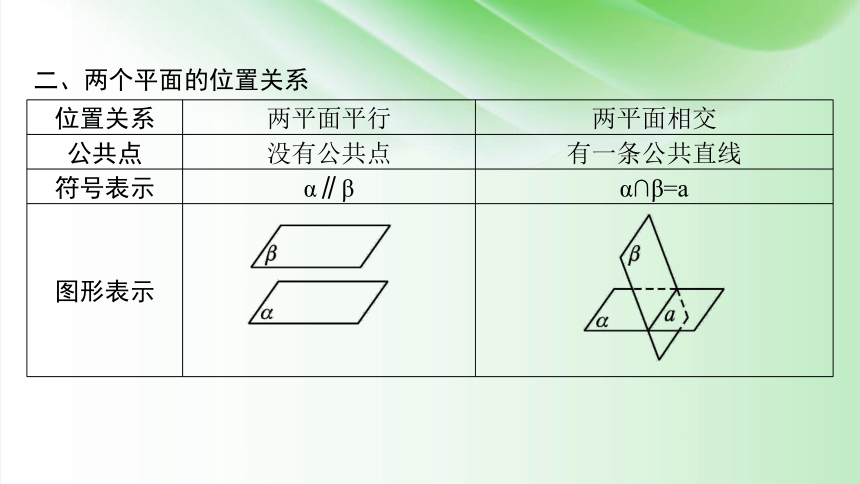
二、两个平面的位置关系
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示 α∥β α∩β=a
图形表示
微练习
如果空间的三个平面两两相交,则下列判断正确的是 (填序号).
①不可能只有两条交线;
②必相交于一点;
③必相交于一条直线;
④必相交于三条平行线.
答案 ①
解析 空间的三个平面两两相交,可能只有一条交线,也可能有三条交线,这三条交线可能交于一点.
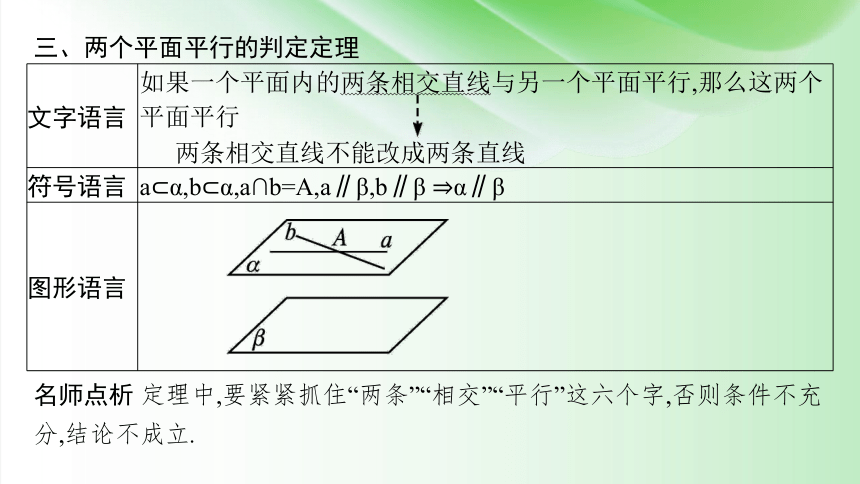
三、两个平面平行的判定定理
文字语言 如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
两条相交直线不能改成两条直线
符号语言 a α,b α,a∩b=A,a∥β,b∥β α∥β
图形语言
名师点析 定理中,要紧紧抓住“两条”“相交”“平行”这六个字,否则条件不充分,结论不成立.
微判断
(1)若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行.( )
(2)若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行.( )
(3)若α∥β,β∥γ,则α∥γ.( )
(4)若a α,α∥β,则a∥β.( )
×
√
√
√
微练习
在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
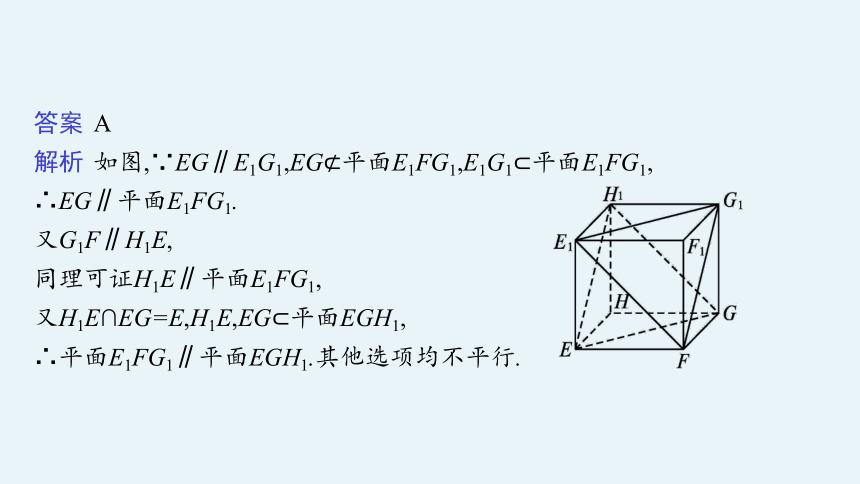
答案 A
解析 如图,∵EG∥E1G1,EG 平面E1FG1,E1G1 平面E1FG1,
∴EG∥平面E1FG1.
又G1F∥H1E,
同理可证H1E∥平面E1FG1,
又H1E∩EG=E,H1E,EG 平面EGH1,
∴平面E1FG1∥平面EGH1.其他选项均不平行.
四、两个平面平行的性质定理
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
符号语言 α∥β,α∩γ=a,β∩γ=b a∥b
图形语言
名师点析 (1)定理成立的条件:两平面平行,第三个平面与这两个平面都相交.
(2)定理的实质——面面平行 线线平行,体现了转化思想与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.
微练习
(1)已知长方体ABCD-A'B'C'D',平面α∩平面ABCD=EF,平面α∩平面A'B'C'D'=E'F',则EF与E'F'的位置关系是( )
A.平行 B.相交 C.异面 D.不确定
(2)若平面α∥平面β,直线a α,点M∈β,过点M的所有直线中( )
A.不一定存在与a平行的直线 B.只有两条与a平行的直线
C.存在无数条与a平行的直线 D.有且只有一条与a平行的直线
答案 (1)A (2)D
解析 (1)由面面平行的性质定理易得.
(2)由于α∥β,a α,M∈β,过M有且只有一条直线与a平行,故D项正确.
五、公垂线与公垂线段
1.与两个平行平面都垂直的直线,叫作这两个平行平面的公垂线,它夹在这两个平行平面间的线段,叫作这两个平行平面的公垂线段.
2.两个平行平面的公垂线段都相等.公垂线段的长度叫作两个平行平面间的距离.
微判断
(1)夹在两平行平面间的平行线段相等.( )
(2)若平面α∥平面β,l 平面β,m 平面α,则直线l与m的距离就是平面α∥平面β间的距离.( )
√
×
探究一
平面与平面平行的判定定理的应用
例1如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明 ∵E,G分别是PC,BC的中点,∴EG∥PB,
又EG 平面PAB,PB 平面PAB,∴EG∥平面PAB.
∵E,F分别是PC,PD的中点,∴EF∥CD,又AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
反思感悟 证明两个平面平行的方法
证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点不容易做到(可用反证法),所以通常用判定定理证明两个平面平行,其步骤如下:
变式训练1如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.求证:
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
证明 (1)∵GH是△A1B1C1的中位线,
∴GH∥B1C1.
又B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.
(2)∵E,F分别为AB,AC的中点,∴EF∥BC.
∵EF 平面BCHG,BC 平面BCHG,∴EF∥平面BCHG.
∵A1G∥EB且A1G=EB,
∴四边形A1EBG是平行四边形,∴A1E∥GB.
∵A1E 平面BCHG,GB 平面BCHG,
∴A1E∥平面BCHG.
∵A1E∩EF=E,A1E,EF 平面EFA1,
∴平面EFA1∥平面BCHG.
探究二
平面与平面平行的性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
分析(1)由面面平行的性质定理直接推证;(2)先由三角形相似得对应线段成比例,再求值.
(1)证明 ∵PB∩PD=P,
∴直线PB和PD确定一个平面γ,
则α∩γ=AC,β∩γ=BD.又α∥β,∴AC∥BD.
(2)解 由(1)得AC∥BD,
2.空间中的计算问题一般利用有关判定或性质定理将原问题转化为平面几何问题,本例就是利用面面平行的性质定理将三维降成二维,最后利用平面几何中的比例性质解决的,体现了转化与化归数学思想的应用.
延伸探究 在本例中,若P在α与β之间,在第(2)问条件下求CD的长.
解 如图,∵PB∩PC=P,
∴PB,PC确定平面γ,γ∩α=AC,γ∩β=BD.
又α∥β,∴AC∥BD,∴△PAC∽△PBD,
探究三
线面平行、面面平行的综合问题
例3如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1,如果存在,请指出并证明你的结论;如果不存在,请说明理由.
分析先找出过DE与平面AB1C1平行的平面,可直接找出过D,E与△AB1C1的三边平行的直线,进而确定平面,然后确定其与棱AB的交点,即可找出E点位置,然后利用定理进行证明即可.
解 当E为棱AB的中点时,DE∥平面AB1C1.
证明如下,
如图所示,取BB1的中点F,连接EF,FD,DE,AC1.
因为D,E,F分别为CC1,AB,BB1的中点,所以EF∥AB1.
因为AB1 平面AB1C1,EF 平面AB1C1,
所以EF∥平面AB1C1.
同理可证FD∥平面AB1C1.
因为EF∩FD=F,EF 平面EFD,FD 平面EFD,所以平面EFD∥平面AB1C1.
因为DE 平面EFD,所以DE∥平面AB1C1.
反思感悟 1.证明直线与平面平行,除了定义法、判定定理法以外,还可以用两平面平行的性质,也就是说为了证明直线与平面平行,也可以先证明两平面平行,再由两平面平行的性质得到线面平行.
2.空间中线线、线面、面面平行关系的转化如下:
变式训练2如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,A1D1的中点.判断直线MN与平面BB1D1D的位置关系,并证明你的结论.
解 MN∥平面BB1D1D,证明如下,
取AD中点E,连接ME,NE,
根据题知ME∥BD,ME 平面BDD1B1,
BD 平面BB1D1D,所以ME∥平面BB1D1D.
又因为NE∥DD1,同理可证NE∥平面BB1D1D,
NE∩EM=E,所以平面EMN∥平面BB1D1D,
因为MN 平面EMN,故MN∥平面BB1D1D.
素养形成
一题多解
典例 已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD的中点.求证:PQ∥平面CBE.
证明 方法一 如图①,取AB的中点G,连接PG和GQ.
因为P是AE的中点,所以PG∥EB.
又PG 平面CBE,EB 平面CBE,
所以PG∥平面CBE.
同理可证GQ∥平面CBE.
又PG∩GQ=G,PG 平面PGQ,GQ 平面PGQ,所以平面PGQ∥平面CBE.因为PQ 平面PGQ,PQ 平面CBE,所以PQ∥平面CBE.
方法二 如图②,连接AC,则Q∈AC,且Q是AC的中点.因为P是AE的中点,所以PQ∥EC.因为PQ 平面CBE,EC 平面CBE,所以PQ∥平面CBE.
方法点睛 线线、线面、面面间的平行关系的判定和性质,常常是通过线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问题时,应抓住“转化”这种思想方法来达到论证的目的.
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.4 平面与平面的位置关系
第2课时 两平面垂直
课标阐释
1.了解二面角及其平面角的概念.(数学抽象)
2.掌握两个平面互相垂直的定义和画法.(直观想象、数学抽象)
3.理解并掌握两个平面垂直的判定定理和性质定理,并能解决有关面面垂直的问题.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
现在建筑师傅在砌墙时,一般不用传统的铅锤,而是采用砌墙红外线仪.该仪器操作方便,测量精确,堪称砌墙神器.如图所示,砌墙时,将该仪器吊放在屋顶,调整好位置和角度,打开仪器后会自动产生横线和竖线,建筑师傅只需顺着光线操作就能保证墙是垂直于地面的.你知道其中的数学原理吗
【知识梳理】
一、二面角
1.一般地,一条直线和由这条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱;每个半平面叫作二面角的面.
2.画法:
3.记法:二面角 α-AB-β 或二面角 α-l-β .
4.二面角的平面角:
(1)若有①O∈l;②OA α,OB β;③OA⊥l,OB⊥l,则二面角α-l-β的平面角是∠AOB .
(2)二面角α的大小范围是0°≤α≤180°.平面角是直角的二面角叫作直二面角.
微思考
(1)平面几何中,“角”是如何定义的
提示 从一点出发的两条射线所组成的图形叫作角.
(2)如图,观察教室内门与墙面,当门绕着门轴旋转时,门所在
的平面与墙面所形成的角的大小和形状.
①数学上,用哪个概念来描述门所在的平面与墙面所形成的角
提示 二面角.
②平时,我们常说“把门开大一点”,在这里指的是哪个角大一点
提示 二面角的平面角.
微练习
在正方体ABCD-A1B1C1D1中,二面角D1-AB-D的平面角的大小是 .
答案 45°
解析 ∵AB⊥平面ADD1A1,∴AB⊥AD,AB⊥AD1,
∴∠D1AD为二面角D1-AB-D的平面角.易知∠D1AD=45°.
微判断
(1)异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角的平面角相等或互补. ( )
(2)二面角的大小与其平面角的顶点在棱上的位置没有关系.( )
√
√
二、平面与平面垂直
1.平面与平面垂直的定义
一般地,如果两个平面所成的二面角是直二面角,那么就说这两个平面互相垂直.
2.平面与平面垂直的判定定理
文字语言 如果一个平面过另一个平面的垂线,那么这两个平面垂直
符号语言 l⊥α,l β α⊥β
图形语言
3.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一条直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直
符号语言 α⊥β,α∩β=l, a α , a⊥l a⊥β
图形语言
名师点析 (1)判定定理可简述为“线面垂直,则面面垂直”.因此要证明平面与平面垂直,可转化为寻找平面的垂线,即证线面垂直.
(2)两个平面互相垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出与一个平面垂直的另一个平面的依据.
(3)此定理有一个推论:a∥α,a⊥β α⊥β.在做选择、填空题时可直接应用.
微思考
(1)如何画两个相互垂直的平面
提示 两个互相垂直的平面通常画成如图中的两种样子,此时,把直立平面的竖边画成与水平平面的横边垂直.
(2)在如图所示的长方体中,AA'与平面ABCD有什么位置关系 AA'在长方体的哪几个面内 这几个面与底面ABCD有什么位置关系
提示 AA'与平面ABCD垂直;AA'在平面AA'B'B内,也在平面AA'D'D内,这两个平面都与底面垂直.
微练习
(1)在三棱锥P-ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,
如图,则在三棱锥P-ABC的四个面中,互相垂直的面
有 对.
答案 3
解析 平面PAB⊥平面PAC,平面PAB⊥平面PBC,平面PAC⊥平面PBC.
(2)已知长方体ABCD-A1B1C1D1,在平面AB1上任取一点M,作ME⊥AB于E,则( )
A.ME⊥平面AC B.ME 平面AC C.ME∥平面AC D.以上都有可能
答案 A
解析 由于ME 平面AB1,平面AB1∩平面AC=AB,且平面AB1⊥平面AC,ME⊥AB,则ME⊥平面AC.
微判断
(1)已知两个平面垂直,则一个平面内已知直线必垂直于另一个平面内的任意一条直线.( )
(2)已知两个平面垂直,则一个平面内的已知直线必垂直于另一个平面的无数条直线.( )
(3)已知两个平面垂直,则过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.( )
×
√
×
探究一
二面角的求法
例1如图,
在正方体ABCD-A'B'C'D'中,
(1)二面角D'-AB-D的大小为 .
(2)二面角A'-AB-D的大小为 .
答案 (1)45° (2)90°
解析 (1)在正方体ABCD-A'B'C'D'中,AB⊥平面AD',所以AB⊥AD',AB⊥AD,因此∠D'AD为二面角D'-AB-D的平面角.在Rt△D'DA中,∠D'AD=45°,所以二面角D'-AB-D的大小为45°.
(2)因为AB⊥平面AD',所以AB⊥AD,AB⊥AA',因此∠A'AD为二面角A'-AB-D的平面角,又∠A'AD=90°,所以二面角A'-AB-D的大小为90°.
要点笔记 在二面角棱上找一特殊点,在两个半平面内分别作垂直于棱的射线,两射线夹角即为所求二面角的平面角.
变式训练1如图,
AB是☉O的直径,PA垂直于☉O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.
解 由已知PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
∵AB是☉O的直径,且点C在圆周上,∴AC⊥BC.
又PA∩AC=A,PA,AC 平面PAC,∴BC⊥平面PAC.
又PC 平面PAC,∴PC⊥BC.
又BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
探究二
平面与平面垂直的判定
例2如图,在四棱锥P-ABCD中,底面ABCD为菱形,PC⊥平面ABCD,求证:平面PDB⊥平面PAC.
证明 ∵PC⊥平面ABCD,BD 平面ABCD,∴PC⊥BD.
∵四边形ABCD为菱形,∴AC⊥BD.
又PC∩AC=C,PC,AC 平面PAC,∴BD⊥平面PAC.
∵BD 平面PBD,∴平面PDB⊥平面PAC.
要点笔记 证明平面与平面垂直的方法
(1)利用定义:证明二面角的平面角为直角.
(2)利用面面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
变式训练2如图,
已知三棱锥S-ABC中,侧棱SA=SB=SC,∠ABC=90°,求证:平面ABC⊥平面ASC.
证明 作SH⊥AC交AC于点H,连接BH,
∵SA=SC,∴AH=HC.
在Rt△ABC中,H是AC的中点,
∴BH= AC=AH.
又SH=SH,SA=SB,
∴△SAH≌△SBH(SSS),∴SH⊥BH.
又AC∩BH=H,AC,BH 平面ABC,
∴SH⊥平面ABC.
又SH 平面ASC,∴平面ABC⊥平面ASC.
探究三
平面与平面垂直的性质定理
例3如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAB⊥平面PBC.求证:BC⊥AB.
证明 如图,在平面PAB内,作AD⊥PB于点D.
∵平面PAB⊥平面PBC,且平面PAB∩平面PBC=PB,AD 平面PAB,
∴AD⊥平面PBC.
又BC 平面PBC,∴AD⊥BC.
又PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
又PA∩AD=A,∴BC⊥平面PAB.
又AB 平面PAB,∴BC⊥AB.
要点笔记 利用面面垂直的性质定理证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.
变式训练3如图,
边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC.求证:AM⊥平面EBC.
证明 ∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC 平面ABC,BC⊥AC,
∴BC⊥平面ACDE.
又AM 平面ACDE,∴BC⊥AM.
∵四边形ACDE是正方形,∴AM⊥CE.
又BC∩CE=C,BC,EC 平面EBC,∴AM⊥平面EBC.
素养形成
思想方法——转化思想在线线、线面、面面垂直中的应用
典例 已知α,β,γ是三个不同的平面,l为直线,α⊥γ,β⊥γ,α∩β=l.求证:l⊥γ.
分析根据直线和平面垂直的判定定理,可在平面γ内构造两相交直线分别与平面α,β垂直;或者由面面垂直的性质易在平面α,β内作出平面γ的垂线,再设法证明l与其平行即可.
证明 方法一 在平面γ内取一点P,作PA垂直平面α与γ的交线于点A,PB垂直β与γ的交线于点B,则PA⊥α,PB⊥β.
∵l=α∩β,∴l⊥PA,l⊥PB.
又PA∩PB=P,且PA γ,PB γ,∴l⊥γ.
方法二 在α内作直线m垂直于α与γ的交线,在β内作直线n垂直于β与γ的交线,
∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ.∴m∥n.
又n β,m β,∴m∥β.又m α,α∩β=l,
∴m∥l.∴l⊥γ.
方法点睛 线线、线面、面面垂直关系的综合应用主要体现了转化思想,其转化关系如下:
谢谢观看
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.4 平面与平面的位置关系
第1课时 两平面平行
课标阐释
1.理解并掌握平面与平面平行的判定定理.(数学抽象)
2.理解并掌握平面与平面平行的性质定理.(数学抽象)
3.能够应用平面与平面平行的判定定理和性质定理证明相关问题.(直观想象、逻辑推理)
4.了解两个平行平面间的距离的概念.(数学抽象)
思维脉络
【激趣诱思】
《老子》中说:“上善若水,水善利万物而不争.”一滴水,可方可圆,泽润万物;一个人,能方能圆,方圆相济,便可活得豁达、圆满.“方中有圆,圆中有方”是大自然的规律,也是为人处世的准则.“天行健,君子以自强不息;地势坤,君子以厚德载物.”在这里,圆是天地周而复始运转不息的象征,方是大地之旷远宽厚稳重的象征.我国古代的钱币,外部是圆形,内部是方孔,看似朴实无华,但蕴含着古人智慧和人生哲理.我们学习过的旋转体圆柱就蕴含着长方形的截面,它是如何得到的 能否用数学原理解释截面的形状
【知识梳理】
一、平面平行和平面相交的定义
1.两个平面互相平行的定义:如果两个平面没有公共点,那么称这两个平面互相平行.
2.两个平面相交的定义:如果两个平面有一个公共点,那么由基本事实3可知,它们相交于经过这个点的一条直线,此时称这两个平面相交.
微思考
两个平面平行,那么两个平面内的所有直线都相互平行吗
提示 不一定.因为两个平面平行,所以分别在这两个平面内的任意两条直线无公共点,它们平行或异面.
二、两个平面的位置关系
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示 α∥β α∩β=a
图形表示
微练习
如果空间的三个平面两两相交,则下列判断正确的是 (填序号).
①不可能只有两条交线;
②必相交于一点;
③必相交于一条直线;
④必相交于三条平行线.
答案 ①
解析 空间的三个平面两两相交,可能只有一条交线,也可能有三条交线,这三条交线可能交于一点.
三、两个平面平行的判定定理
文字语言 如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
两条相交直线不能改成两条直线
符号语言 a α,b α,a∩b=A,a∥β,b∥β α∥β
图形语言
名师点析 定理中,要紧紧抓住“两条”“相交”“平行”这六个字,否则条件不充分,结论不成立.
微判断
(1)若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行.( )
(2)若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行.( )
(3)若α∥β,β∥γ,则α∥γ.( )
(4)若a α,α∥β,则a∥β.( )
×
√
√
√
微练习
在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
答案 A
解析 如图,∵EG∥E1G1,EG 平面E1FG1,E1G1 平面E1FG1,
∴EG∥平面E1FG1.
又G1F∥H1E,
同理可证H1E∥平面E1FG1,
又H1E∩EG=E,H1E,EG 平面EGH1,
∴平面E1FG1∥平面EGH1.其他选项均不平行.
四、两个平面平行的性质定理
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
符号语言 α∥β,α∩γ=a,β∩γ=b a∥b
图形语言
名师点析 (1)定理成立的条件:两平面平行,第三个平面与这两个平面都相交.
(2)定理的实质——面面平行 线线平行,体现了转化思想与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.
微练习
(1)已知长方体ABCD-A'B'C'D',平面α∩平面ABCD=EF,平面α∩平面A'B'C'D'=E'F',则EF与E'F'的位置关系是( )
A.平行 B.相交 C.异面 D.不确定
(2)若平面α∥平面β,直线a α,点M∈β,过点M的所有直线中( )
A.不一定存在与a平行的直线 B.只有两条与a平行的直线
C.存在无数条与a平行的直线 D.有且只有一条与a平行的直线
答案 (1)A (2)D
解析 (1)由面面平行的性质定理易得.
(2)由于α∥β,a α,M∈β,过M有且只有一条直线与a平行,故D项正确.
五、公垂线与公垂线段
1.与两个平行平面都垂直的直线,叫作这两个平行平面的公垂线,它夹在这两个平行平面间的线段,叫作这两个平行平面的公垂线段.
2.两个平行平面的公垂线段都相等.公垂线段的长度叫作两个平行平面间的距离.
微判断
(1)夹在两平行平面间的平行线段相等.( )
(2)若平面α∥平面β,l 平面β,m 平面α,则直线l与m的距离就是平面α∥平面β间的距离.( )
√
×
探究一
平面与平面平行的判定定理的应用
例1如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明 ∵E,G分别是PC,BC的中点,∴EG∥PB,
又EG 平面PAB,PB 平面PAB,∴EG∥平面PAB.
∵E,F分别是PC,PD的中点,∴EF∥CD,又AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
反思感悟 证明两个平面平行的方法
证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点不容易做到(可用反证法),所以通常用判定定理证明两个平面平行,其步骤如下:
变式训练1如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.求证:
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
证明 (1)∵GH是△A1B1C1的中位线,
∴GH∥B1C1.
又B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.
(2)∵E,F分别为AB,AC的中点,∴EF∥BC.
∵EF 平面BCHG,BC 平面BCHG,∴EF∥平面BCHG.
∵A1G∥EB且A1G=EB,
∴四边形A1EBG是平行四边形,∴A1E∥GB.
∵A1E 平面BCHG,GB 平面BCHG,
∴A1E∥平面BCHG.
∵A1E∩EF=E,A1E,EF 平面EFA1,
∴平面EFA1∥平面BCHG.
探究二
平面与平面平行的性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
分析(1)由面面平行的性质定理直接推证;(2)先由三角形相似得对应线段成比例,再求值.
(1)证明 ∵PB∩PD=P,
∴直线PB和PD确定一个平面γ,
则α∩γ=AC,β∩γ=BD.又α∥β,∴AC∥BD.
(2)解 由(1)得AC∥BD,
2.空间中的计算问题一般利用有关判定或性质定理将原问题转化为平面几何问题,本例就是利用面面平行的性质定理将三维降成二维,最后利用平面几何中的比例性质解决的,体现了转化与化归数学思想的应用.
延伸探究 在本例中,若P在α与β之间,在第(2)问条件下求CD的长.
解 如图,∵PB∩PC=P,
∴PB,PC确定平面γ,γ∩α=AC,γ∩β=BD.
又α∥β,∴AC∥BD,∴△PAC∽△PBD,
探究三
线面平行、面面平行的综合问题
例3如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1,如果存在,请指出并证明你的结论;如果不存在,请说明理由.
分析先找出过DE与平面AB1C1平行的平面,可直接找出过D,E与△AB1C1的三边平行的直线,进而确定平面,然后确定其与棱AB的交点,即可找出E点位置,然后利用定理进行证明即可.
解 当E为棱AB的中点时,DE∥平面AB1C1.
证明如下,
如图所示,取BB1的中点F,连接EF,FD,DE,AC1.
因为D,E,F分别为CC1,AB,BB1的中点,所以EF∥AB1.
因为AB1 平面AB1C1,EF 平面AB1C1,
所以EF∥平面AB1C1.
同理可证FD∥平面AB1C1.
因为EF∩FD=F,EF 平面EFD,FD 平面EFD,所以平面EFD∥平面AB1C1.
因为DE 平面EFD,所以DE∥平面AB1C1.
反思感悟 1.证明直线与平面平行,除了定义法、判定定理法以外,还可以用两平面平行的性质,也就是说为了证明直线与平面平行,也可以先证明两平面平行,再由两平面平行的性质得到线面平行.
2.空间中线线、线面、面面平行关系的转化如下:
变式训练2如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,A1D1的中点.判断直线MN与平面BB1D1D的位置关系,并证明你的结论.
解 MN∥平面BB1D1D,证明如下,
取AD中点E,连接ME,NE,
根据题知ME∥BD,ME 平面BDD1B1,
BD 平面BB1D1D,所以ME∥平面BB1D1D.
又因为NE∥DD1,同理可证NE∥平面BB1D1D,
NE∩EM=E,所以平面EMN∥平面BB1D1D,
因为MN 平面EMN,故MN∥平面BB1D1D.
素养形成
一题多解
典例 已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD的中点.求证:PQ∥平面CBE.
证明 方法一 如图①,取AB的中点G,连接PG和GQ.
因为P是AE的中点,所以PG∥EB.
又PG 平面CBE,EB 平面CBE,
所以PG∥平面CBE.
同理可证GQ∥平面CBE.
又PG∩GQ=G,PG 平面PGQ,GQ 平面PGQ,所以平面PGQ∥平面CBE.因为PQ 平面PGQ,PQ 平面CBE,所以PQ∥平面CBE.
方法二 如图②,连接AC,则Q∈AC,且Q是AC的中点.因为P是AE的中点,所以PQ∥EC.因为PQ 平面CBE,EC 平面CBE,所以PQ∥平面CBE.
方法点睛 线线、线面、面面间的平行关系的判定和性质,常常是通过线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问题时,应抓住“转化”这种思想方法来达到论证的目的.
高中数学苏教版必修第二册
第13章 立体几何初步
13.2 基本图形位置关系
13.2.4 平面与平面的位置关系
第2课时 两平面垂直
课标阐释
1.了解二面角及其平面角的概念.(数学抽象)
2.掌握两个平面互相垂直的定义和画法.(直观想象、数学抽象)
3.理解并掌握两个平面垂直的判定定理和性质定理,并能解决有关面面垂直的问题.(逻辑推理、直观想象)
思维脉络
【激趣诱思】
现在建筑师傅在砌墙时,一般不用传统的铅锤,而是采用砌墙红外线仪.该仪器操作方便,测量精确,堪称砌墙神器.如图所示,砌墙时,将该仪器吊放在屋顶,调整好位置和角度,打开仪器后会自动产生横线和竖线,建筑师傅只需顺着光线操作就能保证墙是垂直于地面的.你知道其中的数学原理吗
【知识梳理】
一、二面角
1.一般地,一条直线和由这条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱;每个半平面叫作二面角的面.
2.画法:
3.记法:二面角 α-AB-β 或二面角 α-l-β .
4.二面角的平面角:
(1)若有①O∈l;②OA α,OB β;③OA⊥l,OB⊥l,则二面角α-l-β的平面角是∠AOB .
(2)二面角α的大小范围是0°≤α≤180°.平面角是直角的二面角叫作直二面角.
微思考
(1)平面几何中,“角”是如何定义的
提示 从一点出发的两条射线所组成的图形叫作角.
(2)如图,观察教室内门与墙面,当门绕着门轴旋转时,门所在
的平面与墙面所形成的角的大小和形状.
①数学上,用哪个概念来描述门所在的平面与墙面所形成的角
提示 二面角.
②平时,我们常说“把门开大一点”,在这里指的是哪个角大一点
提示 二面角的平面角.
微练习
在正方体ABCD-A1B1C1D1中,二面角D1-AB-D的平面角的大小是 .
答案 45°
解析 ∵AB⊥平面ADD1A1,∴AB⊥AD,AB⊥AD1,
∴∠D1AD为二面角D1-AB-D的平面角.易知∠D1AD=45°.
微判断
(1)异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角的平面角相等或互补. ( )
(2)二面角的大小与其平面角的顶点在棱上的位置没有关系.( )
√
√
二、平面与平面垂直
1.平面与平面垂直的定义
一般地,如果两个平面所成的二面角是直二面角,那么就说这两个平面互相垂直.
2.平面与平面垂直的判定定理
文字语言 如果一个平面过另一个平面的垂线,那么这两个平面垂直
符号语言 l⊥α,l β α⊥β
图形语言
3.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一条直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直
符号语言 α⊥β,α∩β=l, a α , a⊥l a⊥β
图形语言
名师点析 (1)判定定理可简述为“线面垂直,则面面垂直”.因此要证明平面与平面垂直,可转化为寻找平面的垂线,即证线面垂直.
(2)两个平面互相垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出与一个平面垂直的另一个平面的依据.
(3)此定理有一个推论:a∥α,a⊥β α⊥β.在做选择、填空题时可直接应用.
微思考
(1)如何画两个相互垂直的平面
提示 两个互相垂直的平面通常画成如图中的两种样子,此时,把直立平面的竖边画成与水平平面的横边垂直.
(2)在如图所示的长方体中,AA'与平面ABCD有什么位置关系 AA'在长方体的哪几个面内 这几个面与底面ABCD有什么位置关系
提示 AA'与平面ABCD垂直;AA'在平面AA'B'B内,也在平面AA'D'D内,这两个平面都与底面垂直.
微练习
(1)在三棱锥P-ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,
如图,则在三棱锥P-ABC的四个面中,互相垂直的面
有 对.
答案 3
解析 平面PAB⊥平面PAC,平面PAB⊥平面PBC,平面PAC⊥平面PBC.
(2)已知长方体ABCD-A1B1C1D1,在平面AB1上任取一点M,作ME⊥AB于E,则( )
A.ME⊥平面AC B.ME 平面AC C.ME∥平面AC D.以上都有可能
答案 A
解析 由于ME 平面AB1,平面AB1∩平面AC=AB,且平面AB1⊥平面AC,ME⊥AB,则ME⊥平面AC.
微判断
(1)已知两个平面垂直,则一个平面内已知直线必垂直于另一个平面内的任意一条直线.( )
(2)已知两个平面垂直,则一个平面内的已知直线必垂直于另一个平面的无数条直线.( )
(3)已知两个平面垂直,则过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.( )
×
√
×
探究一
二面角的求法
例1如图,
在正方体ABCD-A'B'C'D'中,
(1)二面角D'-AB-D的大小为 .
(2)二面角A'-AB-D的大小为 .
答案 (1)45° (2)90°
解析 (1)在正方体ABCD-A'B'C'D'中,AB⊥平面AD',所以AB⊥AD',AB⊥AD,因此∠D'AD为二面角D'-AB-D的平面角.在Rt△D'DA中,∠D'AD=45°,所以二面角D'-AB-D的大小为45°.
(2)因为AB⊥平面AD',所以AB⊥AD,AB⊥AA',因此∠A'AD为二面角A'-AB-D的平面角,又∠A'AD=90°,所以二面角A'-AB-D的大小为90°.
要点笔记 在二面角棱上找一特殊点,在两个半平面内分别作垂直于棱的射线,两射线夹角即为所求二面角的平面角.
变式训练1如图,
AB是☉O的直径,PA垂直于☉O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.
解 由已知PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
∵AB是☉O的直径,且点C在圆周上,∴AC⊥BC.
又PA∩AC=A,PA,AC 平面PAC,∴BC⊥平面PAC.
又PC 平面PAC,∴PC⊥BC.
又BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
探究二
平面与平面垂直的判定
例2如图,在四棱锥P-ABCD中,底面ABCD为菱形,PC⊥平面ABCD,求证:平面PDB⊥平面PAC.
证明 ∵PC⊥平面ABCD,BD 平面ABCD,∴PC⊥BD.
∵四边形ABCD为菱形,∴AC⊥BD.
又PC∩AC=C,PC,AC 平面PAC,∴BD⊥平面PAC.
∵BD 平面PBD,∴平面PDB⊥平面PAC.
要点笔记 证明平面与平面垂直的方法
(1)利用定义:证明二面角的平面角为直角.
(2)利用面面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
变式训练2如图,
已知三棱锥S-ABC中,侧棱SA=SB=SC,∠ABC=90°,求证:平面ABC⊥平面ASC.
证明 作SH⊥AC交AC于点H,连接BH,
∵SA=SC,∴AH=HC.
在Rt△ABC中,H是AC的中点,
∴BH= AC=AH.
又SH=SH,SA=SB,
∴△SAH≌△SBH(SSS),∴SH⊥BH.
又AC∩BH=H,AC,BH 平面ABC,
∴SH⊥平面ABC.
又SH 平面ASC,∴平面ABC⊥平面ASC.
探究三
平面与平面垂直的性质定理
例3如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAB⊥平面PBC.求证:BC⊥AB.
证明 如图,在平面PAB内,作AD⊥PB于点D.
∵平面PAB⊥平面PBC,且平面PAB∩平面PBC=PB,AD 平面PAB,
∴AD⊥平面PBC.
又BC 平面PBC,∴AD⊥BC.
又PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
又PA∩AD=A,∴BC⊥平面PAB.
又AB 平面PAB,∴BC⊥AB.
要点笔记 利用面面垂直的性质定理证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.
变式训练3如图,
边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC.求证:AM⊥平面EBC.
证明 ∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC 平面ABC,BC⊥AC,
∴BC⊥平面ACDE.
又AM 平面ACDE,∴BC⊥AM.
∵四边形ACDE是正方形,∴AM⊥CE.
又BC∩CE=C,BC,EC 平面EBC,∴AM⊥平面EBC.
素养形成
思想方法——转化思想在线线、线面、面面垂直中的应用
典例 已知α,β,γ是三个不同的平面,l为直线,α⊥γ,β⊥γ,α∩β=l.求证:l⊥γ.
分析根据直线和平面垂直的判定定理,可在平面γ内构造两相交直线分别与平面α,β垂直;或者由面面垂直的性质易在平面α,β内作出平面γ的垂线,再设法证明l与其平行即可.
证明 方法一 在平面γ内取一点P,作PA垂直平面α与γ的交线于点A,PB垂直β与γ的交线于点B,则PA⊥α,PB⊥β.
∵l=α∩β,∴l⊥PA,l⊥PB.
又PA∩PB=P,且PA γ,PB γ,∴l⊥γ.
方法二 在α内作直线m垂直于α与γ的交线,在β内作直线n垂直于β与γ的交线,
∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ.∴m∥n.
又n β,m β,∴m∥β.又m α,α∩β=l,
∴m∥l.∴l⊥γ.
方法点睛 线线、线面、面面垂直关系的综合应用主要体现了转化思想,其转化关系如下:
谢谢观看
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
