13.3.2 空间图形的体积 课件(共48张PPT) 2023-2024学年高中数学苏教版必修第二册
文档属性
| 名称 | 13.3.2 空间图形的体积 课件(共48张PPT) 2023-2024学年高中数学苏教版必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 18:00:23 | ||
图片预览









文档简介
(共48张PPT)
高中数学苏教版必修第二册
第13章 立体几何初步
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积
第1课时 柱、锥、台的体积
课标阐释
1.掌握柱体、锥体、台体的体积计算公式,会利用它们求有关几何体的体积.(几何直观、数学运算)
2.掌握求几何体体积的基本技巧.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
美国大发明家爱迪生有一位数学基础相当好的助手叫阿普顿.有一次,爱迪生把一只电灯泡的玻璃壳交给阿普顿,要他计算一下灯泡的容积.阿普顿看着梨形的灯泡壳,思索了好久之后,画出了灯泡壳的剖视图、立体图,画出了一条条复杂的曲线,测量了一个个数据,列出了一道道算式.经过几个小时的紧张计算,还未得出结果.结果爱迪生不到一分钟就把灯泡的容积“算”出来了.大家能猜出爱迪生使用的巧妙方法吗
【知识梳理】
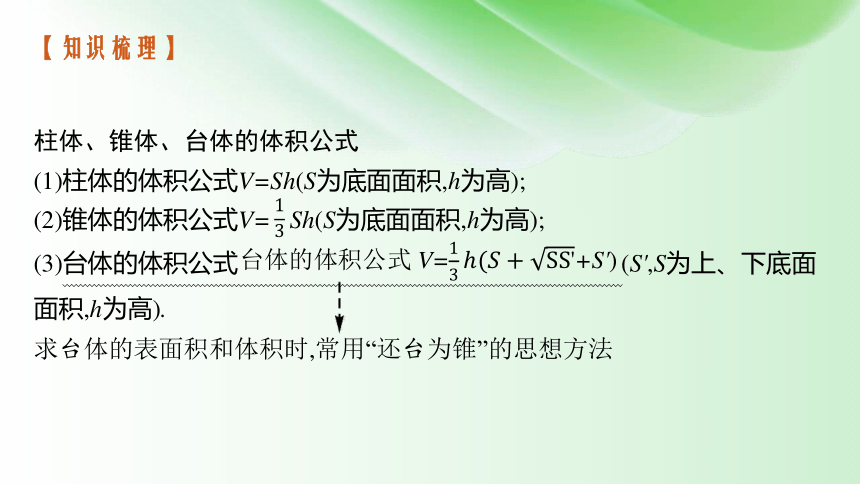
柱体、锥体、台体的体积公式
(1)柱体的体积公式V=Sh(S为底面面积,h为高);
(2)锥体的体积公式V= Sh(S为底面面积,h为高);
(3)台体的体积公式 (S',S为上、下底面面积,h为高).
求台体的表面积和体积时,常用“还台为锥”的思想方法
名师点析 棱柱和圆柱都是柱体,棱锥和圆锥都是锥体,棱台和圆台都是台体,它们的体积公式可统一如下:
(1)V柱体=Sh(S为底面积,h为柱体高);
(2)V锥体= Sh(S为底面积,h为锥体高);
微思考
底面积相等、高也相等的两个锥体,它们的体积相等吗
提示 相等.
微练习
若长方体的长、宽、高分别为3 cm,4 cm,5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3
C.64 cm3 D.125 cm3
答案 B
解析 V长方体=3×4×5=60(cm3).
探究一
柱体体积的计算
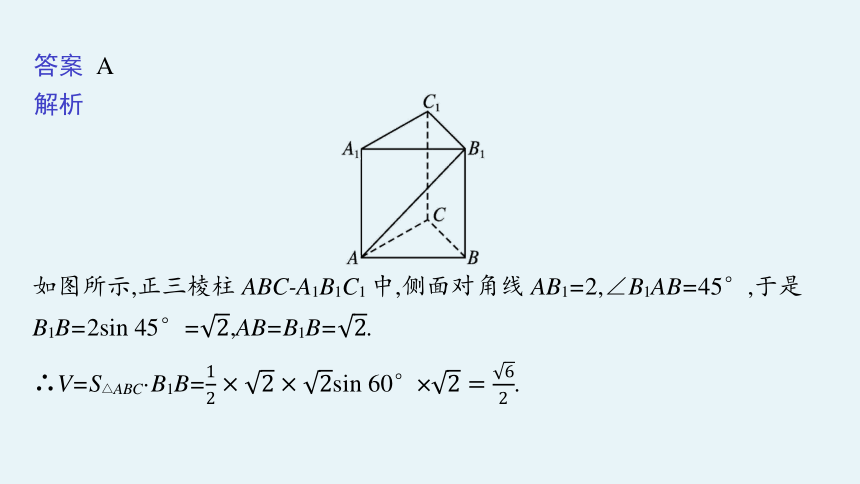
例1正三棱柱侧面的一条对角线长为2,且与该侧面的底边所成的角为45°,则此三棱柱的体积为( )
答案 A
解析
反思感悟 1.求柱体的体积关键是求其底面面积和高,底面面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.一个几何体在空间中可以有不同的放置方法,例如三棱柱既可以把底面放在水平面上,也可以将其中的一个侧面放在水平面上,但在求其体积时,一定要分清棱柱真正的底面,放在水平面上的不一定是底面.
变式训练1(1)已知一个圆柱的底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
(2)已知直三棱柱ABC-A1B1C1,点C到AB的距离为3 cm,侧面ABB1A1的面积为8 cm2,求直三棱柱的体积.
(1)答案 D
解析 V圆柱=πr2h=π×(4÷2)2×4=16π.
(2)解 补上一个相同的直三棱柱ACD-A1C1D1,可以得到一个直四棱柱ABCD-A1B1C1D1.
这个直四棱柱可以看成以ABB1A1为底面的四棱柱DCC1D1-ABB1A1,所以点C到AB的距离即为C到底面ABB1A1的距离,
探究二
锥体体积的计算
例2(1)若圆锥的轴截面是面积为9的等腰直角三角形,则其体积等于 .
(2)如图,正方体ABCD-A1B1C1D1的棱长为a.截面A1DB
将正方体分成两部分,其体积分别为V1,V2,且V2>V1.
①求V1,V2以及V1∶V2;
②求点A到平面A1BD的距离d.
分析(1)首先明确截面将正方体分成的两个几何体的结构特征,然后求出V1,而V2直接用正方体的体积减去V1即得;(2)利用三棱锥的结构特征,根据等积变换列出方程求解.
(1)答案 9π
解析 该圆锥的底面半径为R,由于轴截面是等腰直角三角形,因此圆锥的高为R.
(2)解 ①截面将正方体化为两个几何体,其中较小部分是一个三棱锥
A1-ABD,
反思感悟 1.锥体的体积公式V= Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
2.三棱锥的体积求解具有灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,使得转换后,该三棱锥的底面的面积易求、可求,高易求、可求,这一方法叫作等积法.
3.有些几何体还可以利用分割法或补体法进行求解,无论补体法还是分割法都是要将所给的几何体补成(或分割成)易求解的几何体,体现出间接思维模式和化归的数学思想.
延伸探究 若例2(2)中的正方体改为长方体,则对应截面将该几何体分成两部分的体积之比是否会发生变化 试证明你的结论.
探究三
台体体积的计算
例3圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°,那么该圆台的表面积和体积分别是多少 (结果中保留π)
解 如图所示,设圆台的上底面周长为c,因为扇环的圆心角是180°,所以c=π·SA=2π×10,所以SA=20,同理可得SB=40,所以AB=SB-SA=20,所以S表面积=S侧+S上+S下=π(10+20)×20+π×102+π×202=1 100π(cm2).
故圆台的表面积为1 100π cm2.
要点笔记 求台体体积的一般方法是求出台体的上、下底面的面积和高,然后套用公式 计算求解,要充分利用截面、轴截面、展开图等求出所需要的量,再代入公式计算.
变式训练2体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
答案 A
素养形成
转化思想在求几何体的体积中的应用
典例 1如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
答案 A
典例 2如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
方法点睛 转化思想是解决数学问题的基本思想,它将未知的问题转化为已知问题、复杂问题转化为简单问题,最终将不易解决的问题转化为已解决的问题.如若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行转化求解.
高中数学苏教版必修第二册
第13章 立体几何初步
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积
第2课时 球的表面积和体积
课标阐释
1.了解球的表面积和体积的计算公式的推导过程.(数学模型、逻辑推理)
2.会求解组合体的体积与表面积.(几何直观、数学运算)
3.能用公式解决简单的实际问题.(几何直观、数学运算)
思维脉络
【激趣诱思】
牟合方盖是一种几何体,是两个等半径圆柱躺在平面上垂直相交的公共部分,因为看上去像两个方形的盖子合在一起,所以被称作“牟合方盖”.它是我国古代数学家刘徽发现的一种用于计算球体体积的方式.最初他希望可以用牟合方盖证实《九章算术》的公式有错误,虽然最终并没有实现,但是这个发现有着重要的意义.在刘徽后二百多年贤能之士出现了,这就是中国伟大数学家祖冲之和他的儿子祖暅,他们继承了刘徽的想法,利用了“牟合方盖”彻底解决了球体体积公式的问题.“牟合方盖”的提出,充分体现了古人丰富的想象能力以及为解决问题建立模型的智慧.刘徽是1 700多年前的人,祖氏父子是1 500多年前的人,以千年前的社会知识水平思考这种问题,简直令人叹为观止,这种智慧的光芒,震古烁今,光耀寰宇.他们对数学问题的执着思考与纯粹探索的精神值得现代人学习.以下图示就是推导球体积的模型,它借助了什么数学原理
【知识梳理】
球的表面积与体积公式
微判断
(1)两个球的半径之比为1∶2,则其体积之比为1∶4.( )
(2)球心与其截面圆的圆心的连线垂直于截面.( )
(3)球的表面积等于它的大圆面积的2倍.( )
微练习
把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( )
A.R B.2R C.3R D.4R
答案 D
解析 设圆柱的高为h,则πR2h=3× πR3,得h=4R.
×
√
×
探究一
球的体积和表面积
(2)一个如图所示的密闭容器,它的下部是一个底面半径为1 m、高为2 m的圆锥体,上半部是个半球,则这个密闭容器的表面积是多少 体积为多少
要点笔记 公式是计算球的表面积和体积的关键,半径与球心是确定球的条件.
探究二
球的截面及切、接问题
角度1 球的截面问题
例2一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2,求球的表面积.
解 当截面在球心的同侧时,如图①所示为球的轴截面,由球的截面性质知AO1∥BO2,且O1,O2为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.
设球的半径为R cm,
∵π·O2B2=49π,∴O2B=7 cm.
同理,得O1A=20 cm.
设OO1=x cm,则OO2=(x+9) cm.
在Rt△O1OA中,R2=x2+202,①
在Rt△OO2B中,R2=72+(x+9)2,②
联立①②可得x=15,R=25.
∴S球=4πR2=2 500π(cm2),故球的表面积为2 500π cm2.
①
当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,OO2⊥O2B.设球的半径为R cm,
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.
设O1O=x cm,则OO2=(9-x) cm.
在Rt△OO1A中,R2=x2+400.
在Rt△OO2B中,R2=(9-x)2+49.
∴x2+400=(9-x)2+49,解得x=-15,不合题意,舍去.
综上所述,球的表面积为2 500π cm2.
②
角度2 外接球问题
例3设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2 B.6πa2
C.12πa2 D.24πa2
答案 B
解析
角度3 内切球问题
例4如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则 的值是 .
规律总结 (1)球的截面问题的方法归纳:设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形.解答球的截面问题时,常用该直角三角形求解,并常用过球心和截面圆心的轴截面进行求解.
(2)常见的几何体与球的切、接问题的解决策略:①处理有关几何体外接球或内切球的相关问题时,要注意球心的位置与几何体的关系,一般情况下,由于球的对称性,球心总在特殊位置,比如中心、对角线的中点等.②解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键是根据“切点”和“接点”,作出轴截面图,把空间问题转化为平面问题.
变式训练2(1)将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为 .
(2)在半径为R的球面上有A,B,C三点,且AB=BC=CA=3,球心到△ABC所在截面的距离为球半径的一半,求球的表面积.
素养形成
思想方法——转化与化归思想在球的接、切问题中的应用
典例 在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
分析过正方体的对角面作一截面,在这个截面中用正方体的棱长、球半径的关系求解;或将球补为一个整球,利用球内接长方体求解.
方法二 将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,则这个长方体的对角线便是它的外接球的直径.
设原正方体棱长为a,球的半径为R,则根据长方体的对角线性质,得(2R)2=a2+a2+(2a)2,即4R2=6a2,
方法点睛 球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.
谢谢观看
高中数学苏教版必修第二册
第13章 立体几何初步
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积
第1课时 柱、锥、台的体积
课标阐释
1.掌握柱体、锥体、台体的体积计算公式,会利用它们求有关几何体的体积.(几何直观、数学运算)
2.掌握求几何体体积的基本技巧.(几何直观、逻辑推理)
思维脉络
【激趣诱思】
美国大发明家爱迪生有一位数学基础相当好的助手叫阿普顿.有一次,爱迪生把一只电灯泡的玻璃壳交给阿普顿,要他计算一下灯泡的容积.阿普顿看着梨形的灯泡壳,思索了好久之后,画出了灯泡壳的剖视图、立体图,画出了一条条复杂的曲线,测量了一个个数据,列出了一道道算式.经过几个小时的紧张计算,还未得出结果.结果爱迪生不到一分钟就把灯泡的容积“算”出来了.大家能猜出爱迪生使用的巧妙方法吗
【知识梳理】
柱体、锥体、台体的体积公式
(1)柱体的体积公式V=Sh(S为底面面积,h为高);
(2)锥体的体积公式V= Sh(S为底面面积,h为高);
(3)台体的体积公式 (S',S为上、下底面面积,h为高).
求台体的表面积和体积时,常用“还台为锥”的思想方法
名师点析 棱柱和圆柱都是柱体,棱锥和圆锥都是锥体,棱台和圆台都是台体,它们的体积公式可统一如下:
(1)V柱体=Sh(S为底面积,h为柱体高);
(2)V锥体= Sh(S为底面积,h为锥体高);
微思考
底面积相等、高也相等的两个锥体,它们的体积相等吗
提示 相等.
微练习
若长方体的长、宽、高分别为3 cm,4 cm,5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3
C.64 cm3 D.125 cm3
答案 B
解析 V长方体=3×4×5=60(cm3).
探究一
柱体体积的计算
例1正三棱柱侧面的一条对角线长为2,且与该侧面的底边所成的角为45°,则此三棱柱的体积为( )
答案 A
解析
反思感悟 1.求柱体的体积关键是求其底面面积和高,底面面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.一个几何体在空间中可以有不同的放置方法,例如三棱柱既可以把底面放在水平面上,也可以将其中的一个侧面放在水平面上,但在求其体积时,一定要分清棱柱真正的底面,放在水平面上的不一定是底面.
变式训练1(1)已知一个圆柱的底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
(2)已知直三棱柱ABC-A1B1C1,点C到AB的距离为3 cm,侧面ABB1A1的面积为8 cm2,求直三棱柱的体积.
(1)答案 D
解析 V圆柱=πr2h=π×(4÷2)2×4=16π.
(2)解 补上一个相同的直三棱柱ACD-A1C1D1,可以得到一个直四棱柱ABCD-A1B1C1D1.
这个直四棱柱可以看成以ABB1A1为底面的四棱柱DCC1D1-ABB1A1,所以点C到AB的距离即为C到底面ABB1A1的距离,
探究二
锥体体积的计算
例2(1)若圆锥的轴截面是面积为9的等腰直角三角形,则其体积等于 .
(2)如图,正方体ABCD-A1B1C1D1的棱长为a.截面A1DB
将正方体分成两部分,其体积分别为V1,V2,且V2>V1.
①求V1,V2以及V1∶V2;
②求点A到平面A1BD的距离d.
分析(1)首先明确截面将正方体分成的两个几何体的结构特征,然后求出V1,而V2直接用正方体的体积减去V1即得;(2)利用三棱锥的结构特征,根据等积变换列出方程求解.
(1)答案 9π
解析 该圆锥的底面半径为R,由于轴截面是等腰直角三角形,因此圆锥的高为R.
(2)解 ①截面将正方体化为两个几何体,其中较小部分是一个三棱锥
A1-ABD,
反思感悟 1.锥体的体积公式V= Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
2.三棱锥的体积求解具有灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,使得转换后,该三棱锥的底面的面积易求、可求,高易求、可求,这一方法叫作等积法.
3.有些几何体还可以利用分割法或补体法进行求解,无论补体法还是分割法都是要将所给的几何体补成(或分割成)易求解的几何体,体现出间接思维模式和化归的数学思想.
延伸探究 若例2(2)中的正方体改为长方体,则对应截面将该几何体分成两部分的体积之比是否会发生变化 试证明你的结论.
探究三
台体体积的计算
例3圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°,那么该圆台的表面积和体积分别是多少 (结果中保留π)
解 如图所示,设圆台的上底面周长为c,因为扇环的圆心角是180°,所以c=π·SA=2π×10,所以SA=20,同理可得SB=40,所以AB=SB-SA=20,所以S表面积=S侧+S上+S下=π(10+20)×20+π×102+π×202=1 100π(cm2).
故圆台的表面积为1 100π cm2.
要点笔记 求台体体积的一般方法是求出台体的上、下底面的面积和高,然后套用公式 计算求解,要充分利用截面、轴截面、展开图等求出所需要的量,再代入公式计算.
变式训练2体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
答案 A
素养形成
转化思想在求几何体的体积中的应用
典例 1如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
答案 A
典例 2如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
方法点睛 转化思想是解决数学问题的基本思想,它将未知的问题转化为已知问题、复杂问题转化为简单问题,最终将不易解决的问题转化为已解决的问题.如若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行转化求解.
高中数学苏教版必修第二册
第13章 立体几何初步
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积
第2课时 球的表面积和体积
课标阐释
1.了解球的表面积和体积的计算公式的推导过程.(数学模型、逻辑推理)
2.会求解组合体的体积与表面积.(几何直观、数学运算)
3.能用公式解决简单的实际问题.(几何直观、数学运算)
思维脉络
【激趣诱思】
牟合方盖是一种几何体,是两个等半径圆柱躺在平面上垂直相交的公共部分,因为看上去像两个方形的盖子合在一起,所以被称作“牟合方盖”.它是我国古代数学家刘徽发现的一种用于计算球体体积的方式.最初他希望可以用牟合方盖证实《九章算术》的公式有错误,虽然最终并没有实现,但是这个发现有着重要的意义.在刘徽后二百多年贤能之士出现了,这就是中国伟大数学家祖冲之和他的儿子祖暅,他们继承了刘徽的想法,利用了“牟合方盖”彻底解决了球体体积公式的问题.“牟合方盖”的提出,充分体现了古人丰富的想象能力以及为解决问题建立模型的智慧.刘徽是1 700多年前的人,祖氏父子是1 500多年前的人,以千年前的社会知识水平思考这种问题,简直令人叹为观止,这种智慧的光芒,震古烁今,光耀寰宇.他们对数学问题的执着思考与纯粹探索的精神值得现代人学习.以下图示就是推导球体积的模型,它借助了什么数学原理
【知识梳理】
球的表面积与体积公式
微判断
(1)两个球的半径之比为1∶2,则其体积之比为1∶4.( )
(2)球心与其截面圆的圆心的连线垂直于截面.( )
(3)球的表面积等于它的大圆面积的2倍.( )
微练习
把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( )
A.R B.2R C.3R D.4R
答案 D
解析 设圆柱的高为h,则πR2h=3× πR3,得h=4R.
×
√
×
探究一
球的体积和表面积
(2)一个如图所示的密闭容器,它的下部是一个底面半径为1 m、高为2 m的圆锥体,上半部是个半球,则这个密闭容器的表面积是多少 体积为多少
要点笔记 公式是计算球的表面积和体积的关键,半径与球心是确定球的条件.
探究二
球的截面及切、接问题
角度1 球的截面问题
例2一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2,求球的表面积.
解 当截面在球心的同侧时,如图①所示为球的轴截面,由球的截面性质知AO1∥BO2,且O1,O2为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.
设球的半径为R cm,
∵π·O2B2=49π,∴O2B=7 cm.
同理,得O1A=20 cm.
设OO1=x cm,则OO2=(x+9) cm.
在Rt△O1OA中,R2=x2+202,①
在Rt△OO2B中,R2=72+(x+9)2,②
联立①②可得x=15,R=25.
∴S球=4πR2=2 500π(cm2),故球的表面积为2 500π cm2.
①
当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,OO2⊥O2B.设球的半径为R cm,
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.
设O1O=x cm,则OO2=(9-x) cm.
在Rt△OO1A中,R2=x2+400.
在Rt△OO2B中,R2=(9-x)2+49.
∴x2+400=(9-x)2+49,解得x=-15,不合题意,舍去.
综上所述,球的表面积为2 500π cm2.
②
角度2 外接球问题
例3设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2 B.6πa2
C.12πa2 D.24πa2
答案 B
解析
角度3 内切球问题
例4如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则 的值是 .
规律总结 (1)球的截面问题的方法归纳:设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形.解答球的截面问题时,常用该直角三角形求解,并常用过球心和截面圆心的轴截面进行求解.
(2)常见的几何体与球的切、接问题的解决策略:①处理有关几何体外接球或内切球的相关问题时,要注意球心的位置与几何体的关系,一般情况下,由于球的对称性,球心总在特殊位置,比如中心、对角线的中点等.②解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键是根据“切点”和“接点”,作出轴截面图,把空间问题转化为平面问题.
变式训练2(1)将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为 .
(2)在半径为R的球面上有A,B,C三点,且AB=BC=CA=3,球心到△ABC所在截面的距离为球半径的一半,求球的表面积.
素养形成
思想方法——转化与化归思想在球的接、切问题中的应用
典例 在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
分析过正方体的对角面作一截面,在这个截面中用正方体的棱长、球半径的关系求解;或将球补为一个整球,利用球内接长方体求解.
方法二 将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,则这个长方体的对角线便是它的外接球的直径.
设原正方体棱长为a,球的半径为R,则根据长方体的对角线性质,得(2R)2=a2+a2+(2a)2,即4R2=6a2,
方法点睛 球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.
谢谢观看
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
