比例的应用-比例尺
图片预览

文档简介
课题:比例尺
【教学目的】使学生理解比例尺的含义,会应用比例的知识求平面图的比例尺,以及根据比例尺求图上距离或实际距离。
【教学重点】理解比例尺的意义;能根据比例尺正确求图上距离和实际距离。
【教学难点】设未知数时长度单位的使用。
【教学过程】
一、引入
教师:前面我们学习了比例的知识,比例的知识在实际生活中有什么用途呢?
请同学们看一看我们教室有多大,它的长和宽大约是多少米。(长大约8米,宽大约6米。)如果我们要绘制教室的平面图,若是按实际尺寸来绘制,需要多大的图纸?可能吗?如果要画中国地图呢?于是,人们就想出了一个聪明的办法:在绘制地图和其他平面图的时候,把实际距离按一定的比例缩小,再画在图纸上,有时也把一些尺寸比例小的物体(如机器零件等)的实际距离扩大一定的倍数,再画在图纸上。不管是哪种情况,都需要确定图上距离和实际距离的比。这就是比例的知识在实际生活中的一种应用。今天我们就来学习这方面的知识。
二、教学比例尺的意义。
1.出示图例1:
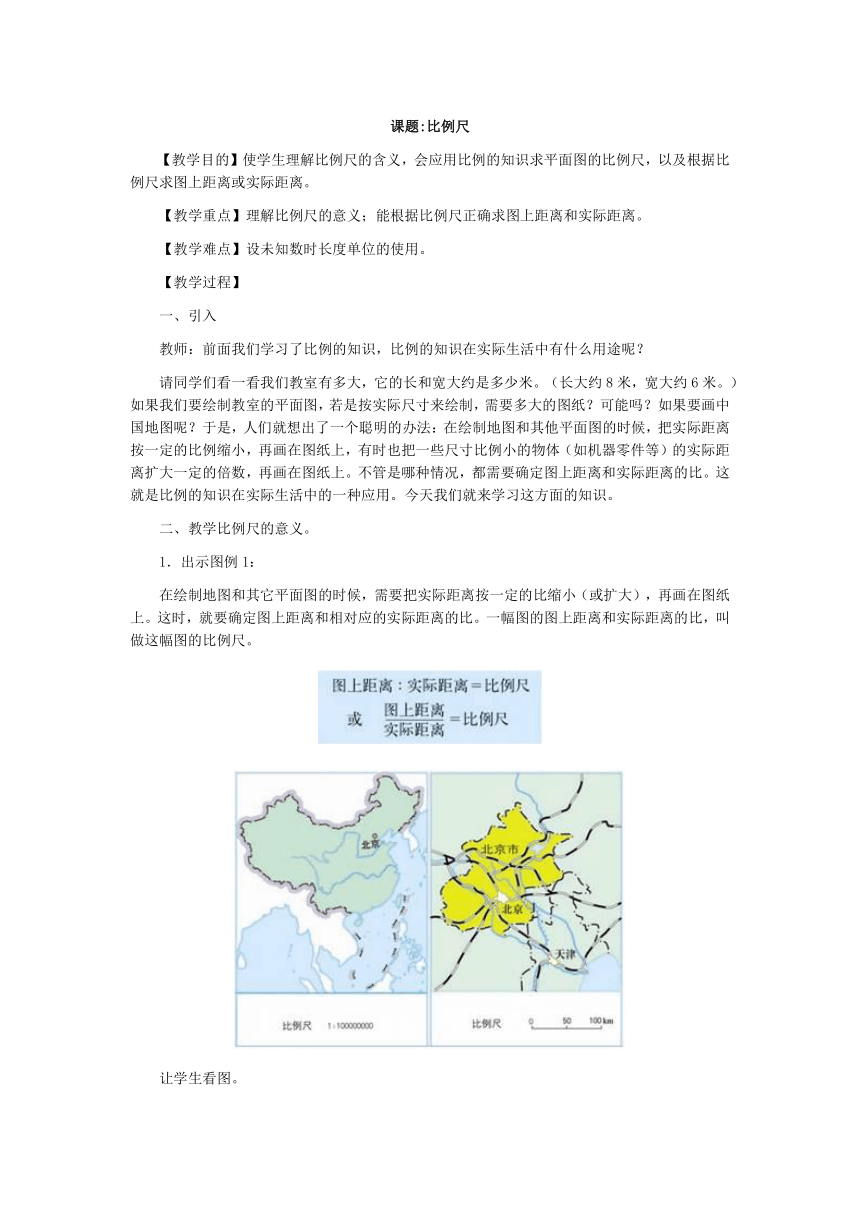
在绘制地图和其它平面图的时候,需要把实际距离按一定的比缩小(或扩大),再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
让学生看图。
“我们经常在地图上看到的比例尺有这两种:1:100000000是数值比例尺,有时也可以写成:,还有一种是线段比例尺(看北京地图),表示地图上1厘米的距离相当于地面上50km的实际距离。”
2.出示图例2
“在生产中,有时由于机器零件比较小,需要把实际距离扩大一定的倍数以后,再画在图纸上。下面就是一个弹簧零件的制作图纸。“
学生看图,“你知道比例‘2:1’表示什么意思吗?这也是一个比例尺,图上距离与实际距离的比是2:1,看一下这个比例尺与前面看到的比例尺有什么不同?”
总结:为了计算方便,通常把比例尺写成前项或后项是1的比。
3.比例尺的化简和转化
“我们再看一下北京地图上的这个线段比例尺,这里图上距离:实际距离=1厘米:50千米,你会把整个比例尺转化成数值比例尺吗?”
说明:这两个数量的单位不同,所以先要把它们化成相同单位,再化简。
“是把厘米化作米,还是把米化作厘米?为什么?”(因为把米化作厘米后实际距离仍是整数,计算起来比较方便,所以要把米化作厘米。)
“50千米等于多少厘米?”学生回答后,教师把50千米改写成5000000厘米。
“现在单位统一了,是多少比多少,怎样化简?”
图上距离:实际距离=1:5000000
教师出示比例尺不同的地图和本地、本校的平面图给学生看,让学生说出它们的比例尺各是多少,表示什么意思。
最后教师指出:
①比例尺与一般的尺不同,这是一个比,不应带计量单位。
②求比例尺时,前、后项的长度单位一定要化成同级单位。如10厘米:10米,要把后项的米化成厘米后再算出比例尺。
③为了计算简便,通常把比例尺的前项化简成“1”,如果写成分数形式,分子也应化简成“1”。
4.巩固练习。
让学生完成第48页的“做一做”。教师可提醒学生注意把图上距离和实际距离的单位化成同级单位。集体订正时,要注意检查学生求出的比例尺的前项是不是“1”。
三、根据比例尺求图上距离或实际距离。
教师:知道了一幅图的比例尺,我们可以根据图上距离求出实际距离,或者根据实际距离求出图上距离。
1.教学例2
下面是北京市地铁规划图。地铁1号线在图中的长度大约是10厘米,它的实际长度大约是多少?
指名读题,并说出题目告诉了什么,要求什么。(告诉了比例尺,又告诉了地铁1号线的的图上距离,求地铁1号线的实际距离。)
教师启发:因为,要求实际距离可以用解比例的方法来求。
“这道题的图上距离是多少?实际距离不知道,怎么办?”“因为图上距离和实际距离的单位要相同,所设的x应用什么单位?(应用厘米。)”
指定一名学生到前面求x的值,其他学生在练习本上做。订正后,回答:
“现在求出的实际距离是多少厘米,为了方便,我们可以将它转化成千米单位。”
2.教学例3:
学校要建一个长80米,宽60米的长方形操场,画出操场的平面图。
指名读题并说出题目告诉了什么?还缺什么条件?(告诉了操场的长和宽的实际距离,但是要画出图还缺少画图设定的比例尺。)
问题:你们觉得该选用多大的比例尺比较好?
学生讨论,教师提出:“1:100或者1:50,这两个比例尺可以吗?”学生继续讨论。进而定比例尺为1:1000。
问题:“确定比例尺后,就需要计算出操场的长和宽在图上的距离,怎么计算呢?”
提示:我们先来求长的图上距离。长的图上距离不知道,应设为x。(板书:解:设长应画x厘米。)长的实际距离是多少?它和图上距离的单位相同吗?怎么办?比例尺是多少?
然后让学生求x的值,并说出求解过程,教师板书出来。
继续求操场宽在图上的距离,可以将宽设为y厘米。让学生把这道题做完。最后教师写出这道题的答。
四、课堂小结
【教学目的】使学生理解比例尺的含义,会应用比例的知识求平面图的比例尺,以及根据比例尺求图上距离或实际距离。
【教学重点】理解比例尺的意义;能根据比例尺正确求图上距离和实际距离。
【教学难点】设未知数时长度单位的使用。
【教学过程】
一、引入
教师:前面我们学习了比例的知识,比例的知识在实际生活中有什么用途呢?
请同学们看一看我们教室有多大,它的长和宽大约是多少米。(长大约8米,宽大约6米。)如果我们要绘制教室的平面图,若是按实际尺寸来绘制,需要多大的图纸?可能吗?如果要画中国地图呢?于是,人们就想出了一个聪明的办法:在绘制地图和其他平面图的时候,把实际距离按一定的比例缩小,再画在图纸上,有时也把一些尺寸比例小的物体(如机器零件等)的实际距离扩大一定的倍数,再画在图纸上。不管是哪种情况,都需要确定图上距离和实际距离的比。这就是比例的知识在实际生活中的一种应用。今天我们就来学习这方面的知识。
二、教学比例尺的意义。
1.出示图例1:
在绘制地图和其它平面图的时候,需要把实际距离按一定的比缩小(或扩大),再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
让学生看图。
“我们经常在地图上看到的比例尺有这两种:1:100000000是数值比例尺,有时也可以写成:,还有一种是线段比例尺(看北京地图),表示地图上1厘米的距离相当于地面上50km的实际距离。”
2.出示图例2
“在生产中,有时由于机器零件比较小,需要把实际距离扩大一定的倍数以后,再画在图纸上。下面就是一个弹簧零件的制作图纸。“
学生看图,“你知道比例‘2:1’表示什么意思吗?这也是一个比例尺,图上距离与实际距离的比是2:1,看一下这个比例尺与前面看到的比例尺有什么不同?”
总结:为了计算方便,通常把比例尺写成前项或后项是1的比。
3.比例尺的化简和转化
“我们再看一下北京地图上的这个线段比例尺,这里图上距离:实际距离=1厘米:50千米,你会把整个比例尺转化成数值比例尺吗?”
说明:这两个数量的单位不同,所以先要把它们化成相同单位,再化简。
“是把厘米化作米,还是把米化作厘米?为什么?”(因为把米化作厘米后实际距离仍是整数,计算起来比较方便,所以要把米化作厘米。)
“50千米等于多少厘米?”学生回答后,教师把50千米改写成5000000厘米。
“现在单位统一了,是多少比多少,怎样化简?”
图上距离:实际距离=1:5000000
教师出示比例尺不同的地图和本地、本校的平面图给学生看,让学生说出它们的比例尺各是多少,表示什么意思。
最后教师指出:
①比例尺与一般的尺不同,这是一个比,不应带计量单位。
②求比例尺时,前、后项的长度单位一定要化成同级单位。如10厘米:10米,要把后项的米化成厘米后再算出比例尺。
③为了计算简便,通常把比例尺的前项化简成“1”,如果写成分数形式,分子也应化简成“1”。
4.巩固练习。
让学生完成第48页的“做一做”。教师可提醒学生注意把图上距离和实际距离的单位化成同级单位。集体订正时,要注意检查学生求出的比例尺的前项是不是“1”。
三、根据比例尺求图上距离或实际距离。
教师:知道了一幅图的比例尺,我们可以根据图上距离求出实际距离,或者根据实际距离求出图上距离。
1.教学例2
下面是北京市地铁规划图。地铁1号线在图中的长度大约是10厘米,它的实际长度大约是多少?
指名读题,并说出题目告诉了什么,要求什么。(告诉了比例尺,又告诉了地铁1号线的的图上距离,求地铁1号线的实际距离。)
教师启发:因为,要求实际距离可以用解比例的方法来求。
“这道题的图上距离是多少?实际距离不知道,怎么办?”“因为图上距离和实际距离的单位要相同,所设的x应用什么单位?(应用厘米。)”
指定一名学生到前面求x的值,其他学生在练习本上做。订正后,回答:
“现在求出的实际距离是多少厘米,为了方便,我们可以将它转化成千米单位。”
2.教学例3:
学校要建一个长80米,宽60米的长方形操场,画出操场的平面图。
指名读题并说出题目告诉了什么?还缺什么条件?(告诉了操场的长和宽的实际距离,但是要画出图还缺少画图设定的比例尺。)
问题:你们觉得该选用多大的比例尺比较好?
学生讨论,教师提出:“1:100或者1:50,这两个比例尺可以吗?”学生继续讨论。进而定比例尺为1:1000。
问题:“确定比例尺后,就需要计算出操场的长和宽在图上的距离,怎么计算呢?”
提示:我们先来求长的图上距离。长的图上距离不知道,应设为x。(板书:解:设长应画x厘米。)长的实际距离是多少?它和图上距离的单位相同吗?怎么办?比例尺是多少?
然后让学生求x的值,并说出求解过程,教师板书出来。
继续求操场宽在图上的距离,可以将宽设为y厘米。让学生把这道题做完。最后教师写出这道题的答。
四、课堂小结
