第五章相交线与平行线素养提优卷(含解析)
文档属性
| 名称 | 第五章相交线与平行线素养提优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 23:22:25 | ||
图片预览

文档简介
第五章 相交线与平行线素养提优卷
考试分数:120分 考试时间:100分钟
一、单选题
1.中图载人航天工程标识主造型既像一个汉语书法的“中”字,又类似空间站的基本形态,尾部的书法笔触似腾空而起的火箭,充满中国元素和航天特色,结构优美、寓意深刻.在选项的四个图中,能由如图经过平移得到的是( )
A. B. C. D.
2.如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.在同一平面内,过直线外一点作的垂线,再过作的垂线,则直线与的位置关系是( )
A.相交 B.相交且垂直 C.平行 D.不能确定
4.数学教学用具:直尺、三角板、量角器如图放置,则的度数是( )
A. B. C. D.
5.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角 B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角 D.同位角、内错角、同旁内角
6.如图,直角三角板的直角顶点落在矩形纸片的一边上.若,则的度数是( )
A. B. C. D.
7.世界上最早记载潜望镜原理的古书,是公元前二世纪中国的《淮南万毕术》.书中记载了这样的一段话:“取大镜高悬,置水盘于其下,则见四邻矣”.现代潜艇潜望镜是在20世纪初发明的.如图是潜望镜工作原理的示意图,那么它所应用的数学原理是( )
A.内错角相等,两直线平行 B.同旁内角互补,两直线平行
C.对顶角相等 D.两点确定一条直线
8.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
9.佳佳和音音在解决如下问题:如图,将三角形的顶点平移到顶点,作出平移后的图形.
佳佳的方法:如图,过点作且使,过点作且使,然后顺次连接、、即可.
音音的方法:如图,过点作且使,过点作且使,然后顺次连接、、即可.
关于这两种方法,下列判断正确的是( )
A.佳佳和音音的方法均正确
B.佳佳的方法正确,音音的方法不正确
C.佳佳的方法不正确,音音的方法正确
D.佳佳和音音的方法均不正确
10.如图,图1是长方形纸带,将纸带沿折叠成图2,再沿折叠成图3.若图1中,,则图3中的的度数是( )
A.120° B.140° C.150° D.160°
二、填空题
11.如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米(填“大于”“小于”或“等于”).
12.中国象棋是中华民族的文化瑰宝,它历史久远、博大精深,如图①,“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置,俗称“马走日”.在如图②所示的象棋盘中,“马”至少走 步才能到达“帅”的位置.
13.如图,一艘船在海面上航行,到达B处时,看到灯塔A在它的北偏东方向,达到C处时,看到灯塔A在它的北偏西方向.则 .
14.学行线后,王玲同学想出了过直线外一点P画直线a的平行线的新方法.他先按照图2动手实验,得到过点P的折线b,此时点A恰好落在直线a上;再按照图3动手实验,得到过点P的折线c,此时点B恰好落在折线b上.王玲同学发现:此时得到的过点P的折线c恰好与直线a平行,他的根据是 .
15.如图为一盏可折叠台灯及其平面示意图,其中支架与底座垂直,支架,为固定支撑杆,当灯体与底座平行时,,,则的度数为 .
三、解答题
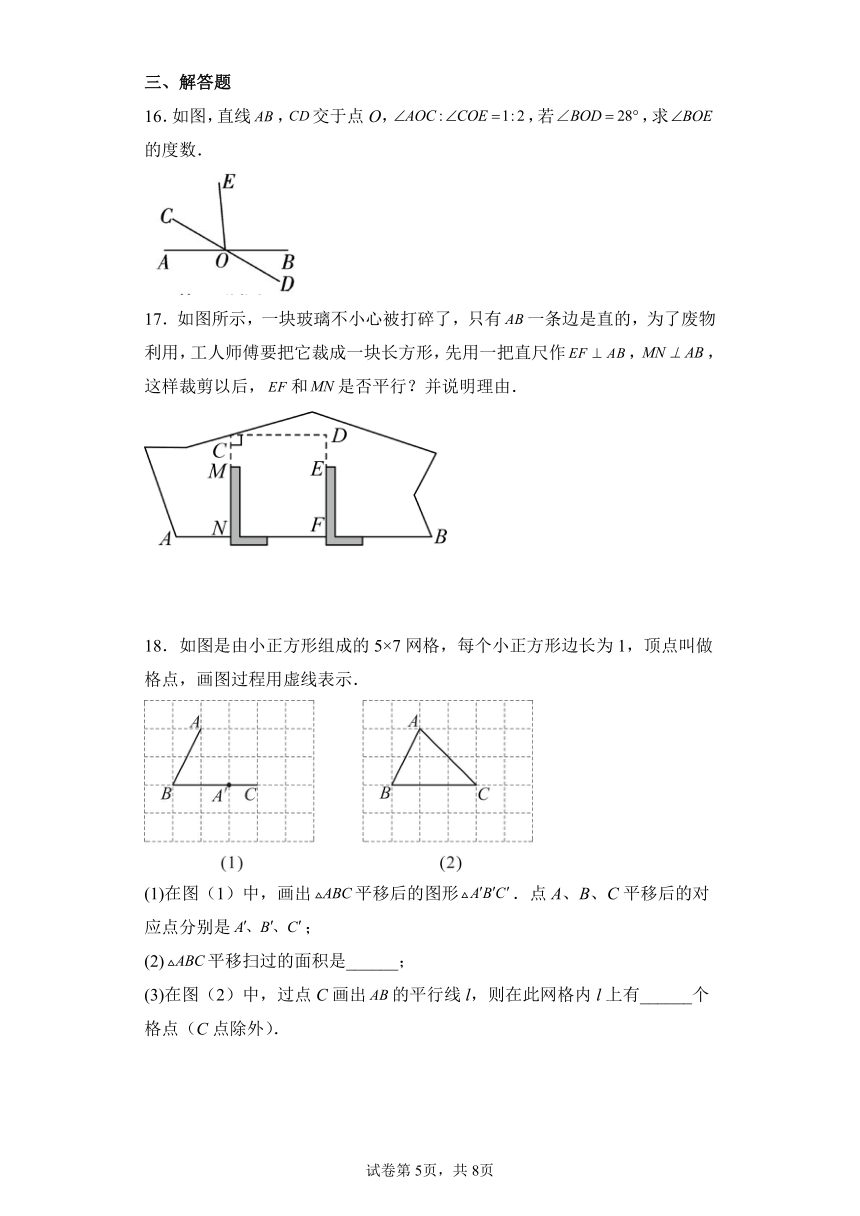
16.如图,直线,交于点O,,若,求的度数.
17.如图所示,一块玻璃不小心被打碎了,只有一条边是直的,为了废物利用,工人师傅要把它裁成一块长方形,先用一把直尺作,,这样裁剪以后,和是否平行?并说明理由.
18.如图是由小正方形组成的5×7网格,每个小正方形边长为1,顶点叫做格点,画图过程用虚线表示.
(1)在图(1)中,画出平移后的图形.点A、B、C平移后的对应点分别是;
(2)平移扫过的面积是______;
(3)在图(2)中,过点C画出的平行线l,则在此网格内l上有______个格点(C点除外).
19.七三班的同学们在学行线与相交线的内容后,进行了自主命题活动,设计出下面的题目.如图所示,现有三个语句①,,②,③.请你以其中两个语句为条件,第三个语句为结论构造命题.
(1)请把你能构造的所有真命题写成“如果……那么……”的形式;
(2)请选择其中的一个真命题进行证明.
20.星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高,宽为 …”
爸爸:(打断小刚的话)“不量每阶的高度和宽度,你想想有没有办法?”
小刚:(思索)“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
21.如图是一种躺椅及其简化结构示意图,扶手与底座都平行于地面,靠背与支架平行,前支架与后支架分别与交于点和点,与交于点,当,时,人躺着最舒服,求此时扶手与支架的夹角和扶手与靠背的夹角的度数.
22.数学课上,老师提出问题:如果两个角的两边分别平行,则这两个角有怎样的数量关系?
小颍认为角的两边是射线,因此要分如下三种情况讨论.请按她的思路完成探究:
问题 已知与,,,探究与的数量关系
情况 ①两边方向均相同,射线与交于点. ②一边方向相同,一边方向相反,射线与交于点. ③两边方向均相反,点在的外部.反向延长射线交射线于点.
图示
结论
说理 ∵, ∴(依据). ∵, ∴, ∴, 即. ∵, ∴, ∵, ∴, ∴, 即.
结论 如果两个角的两边分别平行,则这两个角的数量关系为:_________.
(1)情况①说理过程中的“依据”是: ;
(2)请补全情况②的说理过程;
(3)请补全小颖发现的结论.
23.【学习新知】
射到平面镜上的光线(入射光线)和反射后的光线(反射光线)与平面镜所夹的角相等.如图1,是平面镜,若入射光线与水平镜面的夹角为,反射光线与水平镜面的夹角为,则.
(1)【初步应用】
生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图2当一束“激光”射到平面镜上,被平面镜反射到平面镜上,又被平面镜反射后得到反射光线,回答下列问题:
①当,(即时,求的度数;
②当时,任何射到平面镜上的光线经过平面镜和的两次反射后,入射光线与反射光线总是平行的.请你根据所学知识及新知说明理由.
(提示:三角形的内角和等于
(2)【拓展探究】
如图3,有三块平面镜,,,入射光线经过三次反射,得到反射光线已知,若要使,请直接写出的度数 _____;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据平移的性质:平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等,即可解答;
【详解】如图,可以通过平移节水标志得到的图形是
故选:B
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
2.A
【分析】根据垂线段最短解答即可.
【详解】解:行人沿垂直马路的方向走过斑马线,体现的数学依据是垂线段最短,
故选:A.
【点睛】本题考查垂线段最短,熟知垂线段最短是解答的关键.
3.C
【分析】根据“在同一平面内,垂直于同一直线的两直线互相平行”即可作出判断.
【详解】解:∵在同一平面内,过直线外一点作的垂线,即,
又∵过作的垂线,即,
∴,
∴直线与的位置关系是平行,
故选:C.
【点睛】本题考查平行线的判定.掌握平行线判定的方法是解题的关键.
4.D
【分析】根据题意可得:,,然后利用平行线的性质可得,从而利用平角定义进行计算,即可解答.
【详解】解:如图:
由题意得:,,
,
,
,
故选:D.
【点睛】本题考查了平行线的性质,根据题目的已知条件并几何图形进行分析是解题的关键.
5.D
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.
【详解】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
【点睛】本题考查了同位角、内错角、同旁内角,解题的关键是掌握同位角、内错角、同旁内角,并能区别它们.
6.C
【分析】由平行线的性质和余角的定义求解即可.
【详解】解:如图,
由题意可知,
∴,
∴.
故选C.
【点睛】本题考查三角板中的角度计算,平行线的性质和余角的定义.掌握两直线平行,同位角相等是解题关键.
7.A
【分析】本题考查了平行线的判定.熟练掌握内错角相等,两直线平行是解题的关键.
根据内错角相等,两直线平行进行判断作答即可.
【详解】解:由题意知,所应用的数学原理是内错角相等,两直线平行,
故选:A.
8.D
【分析】根据平行线的判定方法一一判断即可.
【详解】A、由作图可知,内错角相等两直线平行,本选项不符合题意.
B、由作图可知,同位角相等两直线平行,本选项不符合题意.
C、与作图可知,垂直于同一条直线的两条直线平行,本选项不符合题意,
D、无法判断两直线平行,
故选:D.
【点睛】本题考查作图-复杂作图,平行线的判定等知识,解题的关键是读懂图象信息,属于中考常考题型.
9.A
【分析】根据平移的性质分别判断即可.
【详解】解:按照佳佳的方法,且,且,符合图形平移前后对应点连成的线段平行且相等,因此方法正确;
按照音音的方法,,,,, 符合图形平移前后的形状和大小没有变化,只是位置发生变化,因此方法正确;
综上可知,佳佳和音音的方法均正确.
故选A.
【点睛】本题考查图形的平移,解题的关键是掌握平移的性质.图形平移前后的形状和大小没有变化,只是位置发生变化;图形平移后,对应点连成的线段平行(或在同一直线上)且相等.
10.A
【分析】图1中,由题意知,求出图2中,图3中根据求出度数.
【详解】解:图1中,∵矩形对边,
∴,
在图2中,,
在图3中,.
故选:A.
【点睛】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角相等是解题的关键.
11.大于
【详解】解:∵根据跳远成绩为距离起跳线最近的点到起跳线的距离,即垂线段的长,
又∵垂线段最短,
∴小明从起跳点到落脚点之间的距离大于4.6米,
故答案为大于.
12.3
【分析】结合“马走日”规则,分析“马”和“帅”之间相距的格数,并以此作为依据推出“马”行走的步数.
【详解】已知“马”和“帅”之间纵向相距个单位长度,横向相距个单位长度,结合图像进行以下假设:
①如果走步,“马”应落点黄色箭头所指的点,可直观看出无法走到“帅”处;
②如果走步,在①基础上,“马”应落点蓝色箭头所指的点,也无法步到达“帅”点;
③如果走步,在①②基础上,可有条线路能到达“帅”点,如下图绿色箭头所示.
故答案为:.
【点睛】本题考查的是对题意中“马走日”规则的理解,解题关键是结合图像进行假设.
13./75度
【分析】本题考查方向角,关键是掌握方向角的定义.过A作,则,由方向角的定义得到,然后由平行线的性质可得答案.
【详解】解:过A作,则,
由题意得:,
∵,,
∴,
∴,
故答案为:.
14.在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行
【分析】在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.据此即可解答.
【详解】解:由图2可知:,由图3可知:,
∴(在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行).
故答案为:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
【点睛】本题考查了平行线的判定,熟练掌握在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行是解答本题的关键.
15.74
【分析】本题主要考查了平行线的性质与判定,垂线的定义,过点作,过点作,先由垂线的定义得到,则由两直线平行内错角相等得到,证明得到,再根据两直线平行同旁内角互补得到,则.
【详解】解:如图所示,过点作,过点作,
∵,
∴,
∵,
∴,
∵,
∴,
∵,,,
∴,
∴.
∵,,
∴,
∴,
∴.
故答案为:.
16.
【分析】根据对顶角相等求出,根据题意求出,结合图形计算,得到答案.
【详解】解:,
,
,
,
.
【点睛】本题考查的是对顶角、邻补角,熟记对顶角相等是解题的关键.
17.平行,理由见解析.
【分析】根据题意可得,,即可判定.
【详解】解:和平行,理由如下:
∵,
∴
∴
【点睛】此题考查了平行线的应用,解题的关键是掌握平行线的判定方法.
18.(1)见解析
(2)9
(3)2
【分析】本题考查平移的性质.
(1)根据平移的规则,画出即可;
(2)分割法求平移扫过的面积即可;
(3)根据题意,画出直线,确定l上的格点个数即可;
熟练掌握平移的性质,是解题的关键.
【详解】(1)解:如图,即为所求;
(2)由题意,平移扫过的面积为:;
故答案为:9;
(3)如图所示,直线l即为所求,
由图可知,直线上除了格点有2个格点;
故答案为:2.
19.(1)①如图,如果,,,那么,是真命题;
②如图,如果,,,那么,是真命题.
(2)见解析
【分析】(1)结合图形,根据平行线的判定和性质,逐一组合推理判断即可;
(2)利用平行线的判定和性质证明即可;
【详解】(1)①如图,如果,,,那么,是真命题;
②如图,如果,,,那么,是真命题;
(2)命题①正确,证明如下:
,
,
,
,
,
,
,
,
.
命题②正确,证明如下:
,
,
,
,
,
【点睛】本题主要考查平行线的判定和性质的应用,熟练掌握平行线的判定和性质是解题的关键.
20.可以,理由见解析
【分析】根据题意可知地毯的宽度是确定的,求出长即可,再量出楼梯的总高和总长度相加得出答案.
【详解】解:可以,
如图所示:根据图示可得:
地毯的总长度cm=3.15m.
【点睛】本题主要考查了平移的应用,确定地毯的长与楼梯的高和长度的关系是解题的关键.
21.
【分析】先根据平行线的性质,得出,再根据,即可得到,再根据平行线的性质,即可得到的度数,进而得出的度数.
【详解】解:扶手与底座都平行于地面,
,
,
又,
,
,
,
.
【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等;两直线平行,同位角相等.
22.(1)两直线平行,同位角相等
(2)见解析
(3)相等或互补
【分析】(1)根据平行线的性质即可得解;
(2)根据平行线的性质即可得解;
(3)综合①②③的证明,即可得解.
【详解】(1)解:∵,
∴(两直线平行,同位角相等).
∵,
∴,
∴,
即.
故答案为:两直线平行,同位角相等;
(2)解:∵,
∴.
∵,
∴.
∴.
即.
(3)解∶由①③可得,如果两个角的两边分别平行,则这两个角相等,由由②可得,如果两个角的两边分别平行,则这两个角互补.
故答案为:相等或互补.
23.(1)①;②详见解析
(2)
【分析】(1)①由可求,再根据已知的平行条件可得,从而求解;
②由的度数求出,再根据,,可求出,根据平行线的判定和性质可得;
(2)过点作,根据平行公理推论证明,根据平行线的性质,找出角与角之间的关系,求出,,进而可得,在由三角形内角和为,求出.
【详解】(1)解:(①∵,
∴.
又∵,
∴.
②由题意知,.
∵,
∴,
∴,
∴,
∴.
(2)如图,过点作,.
∴.
∵,
∴,
∵,
∴,
∴.
同理可得,
∴.
又∵,
∴,
∴.
故答案为:.
【点睛】本题主要考查了平行线的性质和判定,三角形内角和定理,解题关键是正确识别图形,找出角与角之间的关系.
答案第1页,共2页
答案第1页,共2页
考试分数:120分 考试时间:100分钟
一、单选题
1.中图载人航天工程标识主造型既像一个汉语书法的“中”字,又类似空间站的基本形态,尾部的书法笔触似腾空而起的火箭,充满中国元素和航天特色,结构优美、寓意深刻.在选项的四个图中,能由如图经过平移得到的是( )
A. B. C. D.
2.如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.在同一平面内,过直线外一点作的垂线,再过作的垂线,则直线与的位置关系是( )
A.相交 B.相交且垂直 C.平行 D.不能确定
4.数学教学用具:直尺、三角板、量角器如图放置,则的度数是( )
A. B. C. D.
5.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角 B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角 D.同位角、内错角、同旁内角
6.如图,直角三角板的直角顶点落在矩形纸片的一边上.若,则的度数是( )
A. B. C. D.
7.世界上最早记载潜望镜原理的古书,是公元前二世纪中国的《淮南万毕术》.书中记载了这样的一段话:“取大镜高悬,置水盘于其下,则见四邻矣”.现代潜艇潜望镜是在20世纪初发明的.如图是潜望镜工作原理的示意图,那么它所应用的数学原理是( )
A.内错角相等,两直线平行 B.同旁内角互补,两直线平行
C.对顶角相等 D.两点确定一条直线
8.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
9.佳佳和音音在解决如下问题:如图,将三角形的顶点平移到顶点,作出平移后的图形.
佳佳的方法:如图,过点作且使,过点作且使,然后顺次连接、、即可.
音音的方法:如图,过点作且使,过点作且使,然后顺次连接、、即可.
关于这两种方法,下列判断正确的是( )
A.佳佳和音音的方法均正确
B.佳佳的方法正确,音音的方法不正确
C.佳佳的方法不正确,音音的方法正确
D.佳佳和音音的方法均不正确
10.如图,图1是长方形纸带,将纸带沿折叠成图2,再沿折叠成图3.若图1中,,则图3中的的度数是( )
A.120° B.140° C.150° D.160°
二、填空题
11.如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米(填“大于”“小于”或“等于”).
12.中国象棋是中华民族的文化瑰宝,它历史久远、博大精深,如图①,“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置,俗称“马走日”.在如图②所示的象棋盘中,“马”至少走 步才能到达“帅”的位置.
13.如图,一艘船在海面上航行,到达B处时,看到灯塔A在它的北偏东方向,达到C处时,看到灯塔A在它的北偏西方向.则 .
14.学行线后,王玲同学想出了过直线外一点P画直线a的平行线的新方法.他先按照图2动手实验,得到过点P的折线b,此时点A恰好落在直线a上;再按照图3动手实验,得到过点P的折线c,此时点B恰好落在折线b上.王玲同学发现:此时得到的过点P的折线c恰好与直线a平行,他的根据是 .
15.如图为一盏可折叠台灯及其平面示意图,其中支架与底座垂直,支架,为固定支撑杆,当灯体与底座平行时,,,则的度数为 .
三、解答题
16.如图,直线,交于点O,,若,求的度数.
17.如图所示,一块玻璃不小心被打碎了,只有一条边是直的,为了废物利用,工人师傅要把它裁成一块长方形,先用一把直尺作,,这样裁剪以后,和是否平行?并说明理由.
18.如图是由小正方形组成的5×7网格,每个小正方形边长为1,顶点叫做格点,画图过程用虚线表示.
(1)在图(1)中,画出平移后的图形.点A、B、C平移后的对应点分别是;
(2)平移扫过的面积是______;
(3)在图(2)中,过点C画出的平行线l,则在此网格内l上有______个格点(C点除外).
19.七三班的同学们在学行线与相交线的内容后,进行了自主命题活动,设计出下面的题目.如图所示,现有三个语句①,,②,③.请你以其中两个语句为条件,第三个语句为结论构造命题.
(1)请把你能构造的所有真命题写成“如果……那么……”的形式;
(2)请选择其中的一个真命题进行证明.
20.星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高,宽为 …”
爸爸:(打断小刚的话)“不量每阶的高度和宽度,你想想有没有办法?”
小刚:(思索)“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
21.如图是一种躺椅及其简化结构示意图,扶手与底座都平行于地面,靠背与支架平行,前支架与后支架分别与交于点和点,与交于点,当,时,人躺着最舒服,求此时扶手与支架的夹角和扶手与靠背的夹角的度数.
22.数学课上,老师提出问题:如果两个角的两边分别平行,则这两个角有怎样的数量关系?
小颍认为角的两边是射线,因此要分如下三种情况讨论.请按她的思路完成探究:
问题 已知与,,,探究与的数量关系
情况 ①两边方向均相同,射线与交于点. ②一边方向相同,一边方向相反,射线与交于点. ③两边方向均相反,点在的外部.反向延长射线交射线于点.
图示
结论
说理 ∵, ∴(依据). ∵, ∴, ∴, 即. ∵, ∴, ∵, ∴, ∴, 即.
结论 如果两个角的两边分别平行,则这两个角的数量关系为:_________.
(1)情况①说理过程中的“依据”是: ;
(2)请补全情况②的说理过程;
(3)请补全小颖发现的结论.
23.【学习新知】
射到平面镜上的光线(入射光线)和反射后的光线(反射光线)与平面镜所夹的角相等.如图1,是平面镜,若入射光线与水平镜面的夹角为,反射光线与水平镜面的夹角为,则.
(1)【初步应用】
生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图2当一束“激光”射到平面镜上,被平面镜反射到平面镜上,又被平面镜反射后得到反射光线,回答下列问题:
①当,(即时,求的度数;
②当时,任何射到平面镜上的光线经过平面镜和的两次反射后,入射光线与反射光线总是平行的.请你根据所学知识及新知说明理由.
(提示:三角形的内角和等于
(2)【拓展探究】
如图3,有三块平面镜,,,入射光线经过三次反射,得到反射光线已知,若要使,请直接写出的度数 _____;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据平移的性质:平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等,即可解答;
【详解】如图,可以通过平移节水标志得到的图形是
故选:B
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
2.A
【分析】根据垂线段最短解答即可.
【详解】解:行人沿垂直马路的方向走过斑马线,体现的数学依据是垂线段最短,
故选:A.
【点睛】本题考查垂线段最短,熟知垂线段最短是解答的关键.
3.C
【分析】根据“在同一平面内,垂直于同一直线的两直线互相平行”即可作出判断.
【详解】解:∵在同一平面内,过直线外一点作的垂线,即,
又∵过作的垂线,即,
∴,
∴直线与的位置关系是平行,
故选:C.
【点睛】本题考查平行线的判定.掌握平行线判定的方法是解题的关键.
4.D
【分析】根据题意可得:,,然后利用平行线的性质可得,从而利用平角定义进行计算,即可解答.
【详解】解:如图:
由题意得:,,
,
,
,
故选:D.
【点睛】本题考查了平行线的性质,根据题目的已知条件并几何图形进行分析是解题的关键.
5.D
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.
【详解】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
【点睛】本题考查了同位角、内错角、同旁内角,解题的关键是掌握同位角、内错角、同旁内角,并能区别它们.
6.C
【分析】由平行线的性质和余角的定义求解即可.
【详解】解:如图,
由题意可知,
∴,
∴.
故选C.
【点睛】本题考查三角板中的角度计算,平行线的性质和余角的定义.掌握两直线平行,同位角相等是解题关键.
7.A
【分析】本题考查了平行线的判定.熟练掌握内错角相等,两直线平行是解题的关键.
根据内错角相等,两直线平行进行判断作答即可.
【详解】解:由题意知,所应用的数学原理是内错角相等,两直线平行,
故选:A.
8.D
【分析】根据平行线的判定方法一一判断即可.
【详解】A、由作图可知,内错角相等两直线平行,本选项不符合题意.
B、由作图可知,同位角相等两直线平行,本选项不符合题意.
C、与作图可知,垂直于同一条直线的两条直线平行,本选项不符合题意,
D、无法判断两直线平行,
故选:D.
【点睛】本题考查作图-复杂作图,平行线的判定等知识,解题的关键是读懂图象信息,属于中考常考题型.
9.A
【分析】根据平移的性质分别判断即可.
【详解】解:按照佳佳的方法,且,且,符合图形平移前后对应点连成的线段平行且相等,因此方法正确;
按照音音的方法,,,,, 符合图形平移前后的形状和大小没有变化,只是位置发生变化,因此方法正确;
综上可知,佳佳和音音的方法均正确.
故选A.
【点睛】本题考查图形的平移,解题的关键是掌握平移的性质.图形平移前后的形状和大小没有变化,只是位置发生变化;图形平移后,对应点连成的线段平行(或在同一直线上)且相等.
10.A
【分析】图1中,由题意知,求出图2中,图3中根据求出度数.
【详解】解:图1中,∵矩形对边,
∴,
在图2中,,
在图3中,.
故选:A.
【点睛】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角相等是解题的关键.
11.大于
【详解】解:∵根据跳远成绩为距离起跳线最近的点到起跳线的距离,即垂线段的长,
又∵垂线段最短,
∴小明从起跳点到落脚点之间的距离大于4.6米,
故答案为大于.
12.3
【分析】结合“马走日”规则,分析“马”和“帅”之间相距的格数,并以此作为依据推出“马”行走的步数.
【详解】已知“马”和“帅”之间纵向相距个单位长度,横向相距个单位长度,结合图像进行以下假设:
①如果走步,“马”应落点黄色箭头所指的点,可直观看出无法走到“帅”处;
②如果走步,在①基础上,“马”应落点蓝色箭头所指的点,也无法步到达“帅”点;
③如果走步,在①②基础上,可有条线路能到达“帅”点,如下图绿色箭头所示.
故答案为:.
【点睛】本题考查的是对题意中“马走日”规则的理解,解题关键是结合图像进行假设.
13./75度
【分析】本题考查方向角,关键是掌握方向角的定义.过A作,则,由方向角的定义得到,然后由平行线的性质可得答案.
【详解】解:过A作,则,
由题意得:,
∵,,
∴,
∴,
故答案为:.
14.在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行
【分析】在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.据此即可解答.
【详解】解:由图2可知:,由图3可知:,
∴(在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行).
故答案为:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
【点睛】本题考查了平行线的判定,熟练掌握在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行是解答本题的关键.
15.74
【分析】本题主要考查了平行线的性质与判定,垂线的定义,过点作,过点作,先由垂线的定义得到,则由两直线平行内错角相等得到,证明得到,再根据两直线平行同旁内角互补得到,则.
【详解】解:如图所示,过点作,过点作,
∵,
∴,
∵,
∴,
∵,
∴,
∵,,,
∴,
∴.
∵,,
∴,
∴,
∴.
故答案为:.
16.
【分析】根据对顶角相等求出,根据题意求出,结合图形计算,得到答案.
【详解】解:,
,
,
,
.
【点睛】本题考查的是对顶角、邻补角,熟记对顶角相等是解题的关键.
17.平行,理由见解析.
【分析】根据题意可得,,即可判定.
【详解】解:和平行,理由如下:
∵,
∴
∴
【点睛】此题考查了平行线的应用,解题的关键是掌握平行线的判定方法.
18.(1)见解析
(2)9
(3)2
【分析】本题考查平移的性质.
(1)根据平移的规则,画出即可;
(2)分割法求平移扫过的面积即可;
(3)根据题意,画出直线,确定l上的格点个数即可;
熟练掌握平移的性质,是解题的关键.
【详解】(1)解:如图,即为所求;
(2)由题意,平移扫过的面积为:;
故答案为:9;
(3)如图所示,直线l即为所求,
由图可知,直线上除了格点有2个格点;
故答案为:2.
19.(1)①如图,如果,,,那么,是真命题;
②如图,如果,,,那么,是真命题.
(2)见解析
【分析】(1)结合图形,根据平行线的判定和性质,逐一组合推理判断即可;
(2)利用平行线的判定和性质证明即可;
【详解】(1)①如图,如果,,,那么,是真命题;
②如图,如果,,,那么,是真命题;
(2)命题①正确,证明如下:
,
,
,
,
,
,
,
,
.
命题②正确,证明如下:
,
,
,
,
,
【点睛】本题主要考查平行线的判定和性质的应用,熟练掌握平行线的判定和性质是解题的关键.
20.可以,理由见解析
【分析】根据题意可知地毯的宽度是确定的,求出长即可,再量出楼梯的总高和总长度相加得出答案.
【详解】解:可以,
如图所示:根据图示可得:
地毯的总长度cm=3.15m.
【点睛】本题主要考查了平移的应用,确定地毯的长与楼梯的高和长度的关系是解题的关键.
21.
【分析】先根据平行线的性质,得出,再根据,即可得到,再根据平行线的性质,即可得到的度数,进而得出的度数.
【详解】解:扶手与底座都平行于地面,
,
,
又,
,
,
,
.
【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等;两直线平行,同位角相等.
22.(1)两直线平行,同位角相等
(2)见解析
(3)相等或互补
【分析】(1)根据平行线的性质即可得解;
(2)根据平行线的性质即可得解;
(3)综合①②③的证明,即可得解.
【详解】(1)解:∵,
∴(两直线平行,同位角相等).
∵,
∴,
∴,
即.
故答案为:两直线平行,同位角相等;
(2)解:∵,
∴.
∵,
∴.
∴.
即.
(3)解∶由①③可得,如果两个角的两边分别平行,则这两个角相等,由由②可得,如果两个角的两边分别平行,则这两个角互补.
故答案为:相等或互补.
23.(1)①;②详见解析
(2)
【分析】(1)①由可求,再根据已知的平行条件可得,从而求解;
②由的度数求出,再根据,,可求出,根据平行线的判定和性质可得;
(2)过点作,根据平行公理推论证明,根据平行线的性质,找出角与角之间的关系,求出,,进而可得,在由三角形内角和为,求出.
【详解】(1)解:(①∵,
∴.
又∵,
∴.
②由题意知,.
∵,
∴,
∴,
∴,
∴.
(2)如图,过点作,.
∴.
∵,
∴,
∵,
∴,
∴.
同理可得,
∴.
又∵,
∴,
∴.
故答案为:.
【点睛】本题主要考查了平行线的性质和判定,三角形内角和定理,解题关键是正确识别图形,找出角与角之间的关系.
答案第1页,共2页
答案第1页,共2页
