广东省深圳市重点中学2023-2024学年下学期九年级开学考数学试卷(无答案)
文档属性
| 名称 | 广东省深圳市重点中学2023-2024学年下学期九年级开学考数学试卷(无答案) |

|
|
| 格式 | |||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览

文档简介
南实集团麒麟中学 2023-2024学年第二学期九年级开学考数学试卷
一.选择题(每题 3 分,共 30 分)
1.如图所示的是某用户微信支付情况,﹣100表示的意思是( )
A.发出 100元红包 B.收入 100元
C.余额 100元 D.抢到 100元红包
2.九(1)班选派 4名学生参加演讲比赛,他们的成绩如下:
选手 A B C D 平均成绩 中位数
成绩/分 86 ■ 82 88 85 ■
则如表中被遮盖的两个数据从左到右依次是( )
A.84,86 B.84,85 C.82,86 D.82,87
3.如图是一个正方体的平面展开图,若正方体中相对的面上的数字或代数式的乘积都小于 0,则整数 x的值是( )
A.0 B.1 C.﹣1 D.2
4.下列运算正确的是( )
A.(x+2)2=x2+4 B.a2 a4=a8
C.(2x3)2=4x6 D.2x2+3x2=5x4
5.将一把直尺和一块含 30°和 60°角的三角板 ABC按如图所示的位置放置,如果∠CDE=45°,那么∠BAF的
大小为( )
第 1页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
A.15° B.10° C.20° D.25°
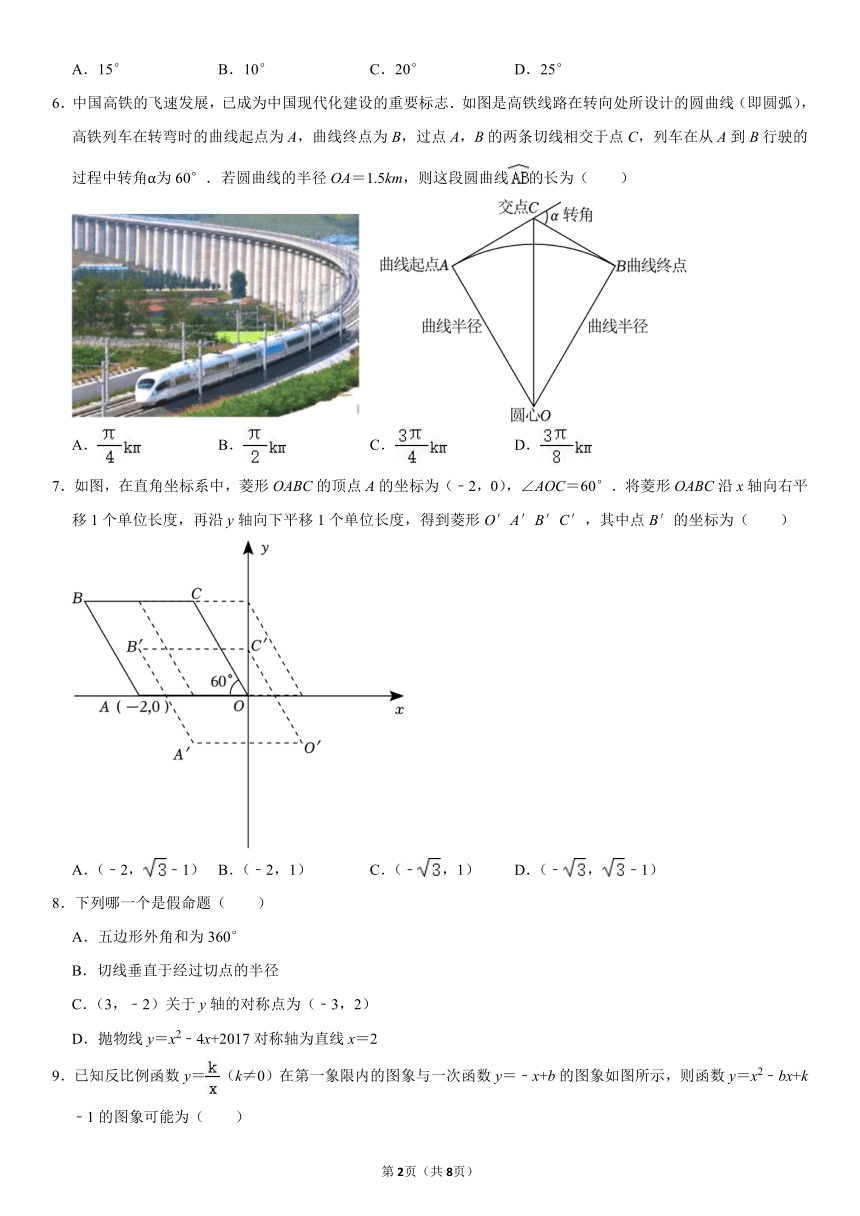
6.中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),
高铁列车在转弯时的曲线起点为 A,曲线终点为 B,过点 A,B的两条切线相交于点 C,列车在从 A到 B行驶的
过程中转角α为 60°.若圆曲线的半径 OA=1.5km,则这段圆曲线 的长为( )
A. B. C. D.
7.如图,在直角坐标系中,菱形 OABC的顶点 A的坐标为(﹣2,0),∠AOC=60°.将菱形 OABC沿 x轴向右平
移 1个单位长度,再沿 y轴向下平移 1个单位长度,得到菱形 O′A′B′C′,其中点 B′的坐标为( )
A.(﹣2, ﹣1) B.(﹣2,1) C.(﹣ ,1) D.(﹣ , ﹣1)
8.下列哪一个是假命题( )
A.五边形外角和为 360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于 y轴的对称点为(﹣3,2)
D.抛物线 y=x2﹣4x+2017对称轴为直线 x=2
9.已知反比例函数 y= (k≠0)在第一象限内的图象与一次函数 y=﹣x+b的图象如图所示,则函数 y=x2﹣bx+k
﹣1的图象可能为( )
第 2页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
A. B. C. D.
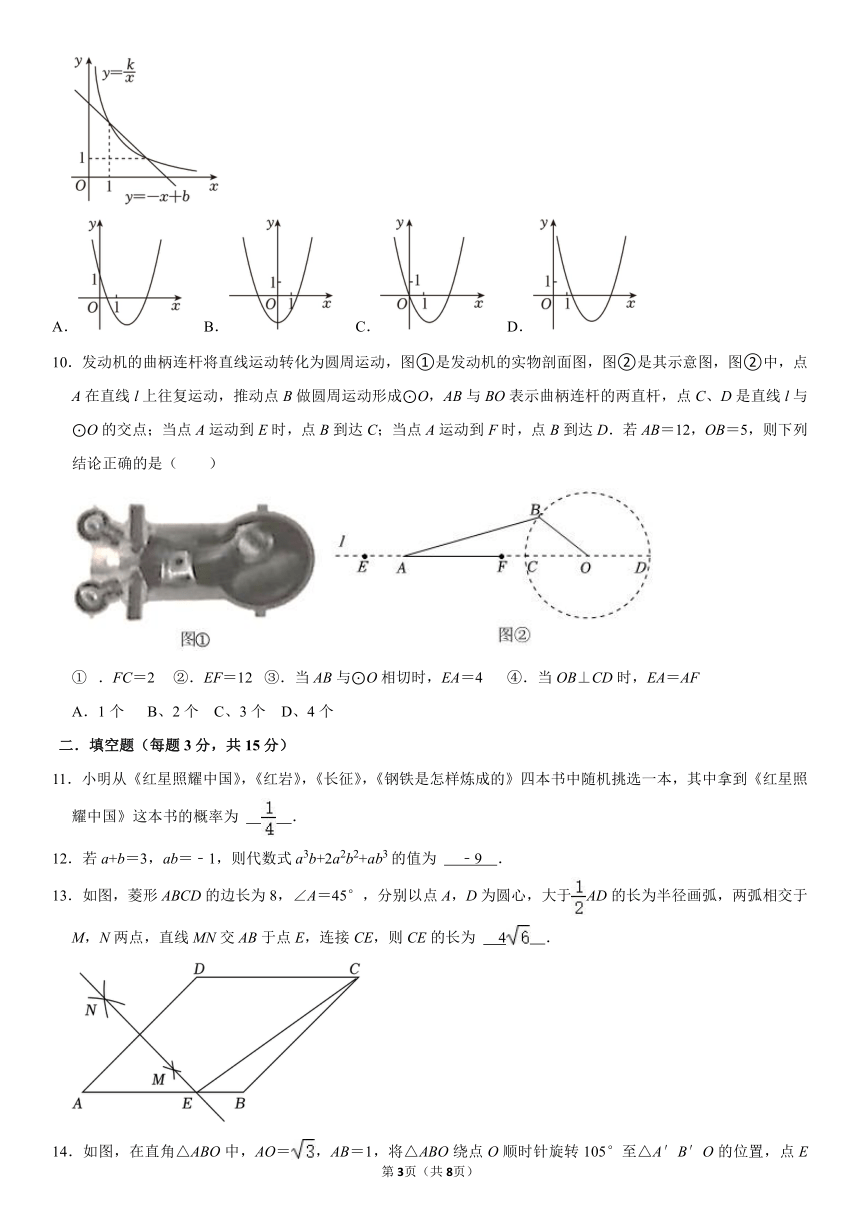
10.发动机的曲柄连杆将直线运动转化为圆周运动,图①是发动机的实物剖面图,图②是其示意图,图②中,点
A在直线 l上往复运动,推动点 B做圆周运动形成⊙O,AB与 BO表示曲柄连杆的两直杆,点 C、D是直线 l与
⊙O的交点;当点 A运动到 E时,点 B到达 C;当点 A运动到 F时,点 B到达 D.若 AB=12,OB=5,则下列
结论正确的是( )
① .FC=2 ②.EF=12 ③.当 AB与⊙O相切时,EA=4 ④.当 OB⊥CD时,EA=AF
A.1个 B、2个 C、3个 D、4个
声明:试题解析著作二.填空题(每题 3 分,共 15 分)
11.小明从《红星照耀中国》,《红岩》,《长征》,《钢铁是怎样炼成的》四本书中随机挑选一本,其中拿到《红星照
耀中国》这本书的概率为 .
12.若 a+b=3,ab=﹣1,则代数式 a3b+2a2b2+ab3的值为 ﹣9 .
13.如图,菱形 ABCD的边长为 8,∠A=45°,分别以点 A,D为圆心,大于 AD的长为半径画弧,两弧相交于
M,N两点,直线 MN交 AB于点 E,连接 CE,则 CE的长为 4 .
14.如图,在直角△ABO中,AO= ,AB=1,将△ABO绕点 O顺时针旋转 105°至△A′B′O的位置,点 E
第 3页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
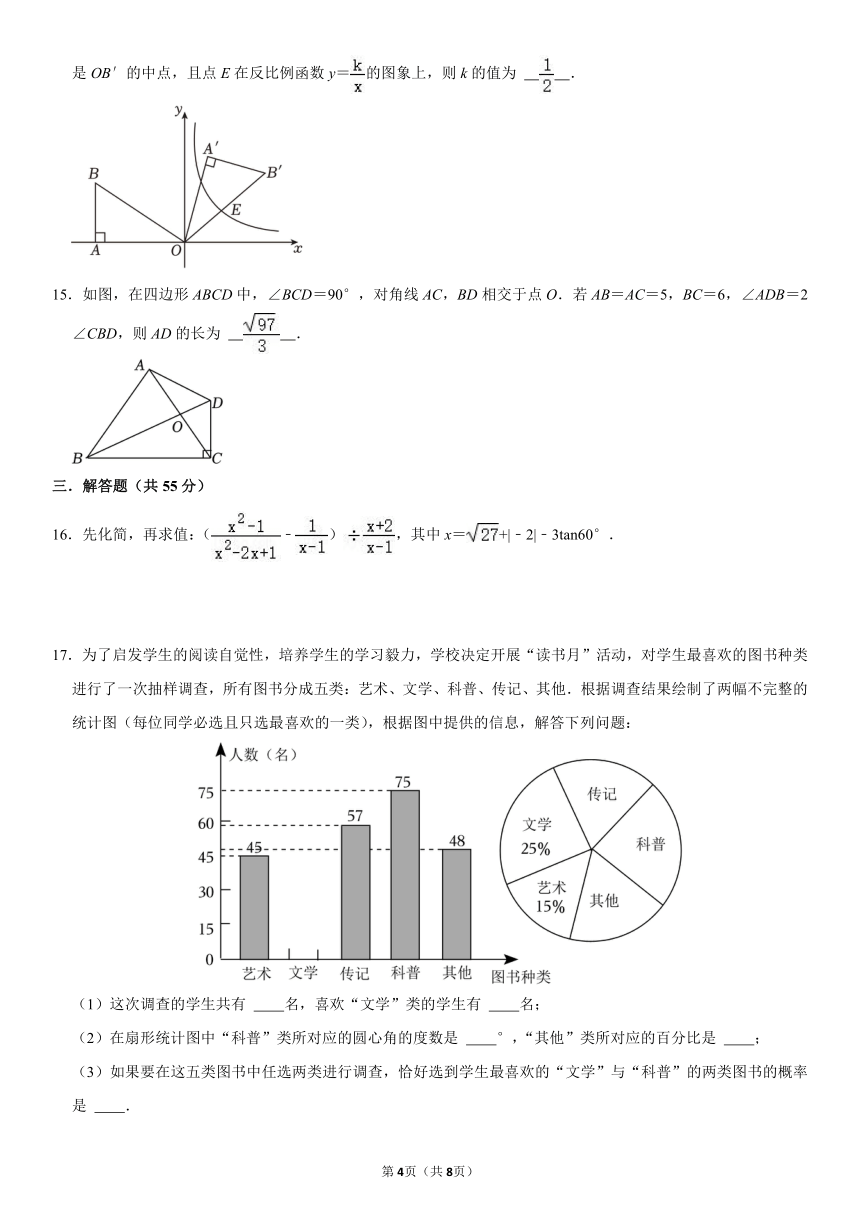
是 OB′的中点,且点 E在反比例函数 y= 的图象上,则 k的值为 .
15.如图,在四边形 ABCD中,∠BCD=90°,对角线 AC,BD相交于点 O.若 AB=AC=5,BC=6,∠ADB=2
∠CBD,则 AD的长为 .
三.解答题(共 55 分)
16.先化简,再求值:( ﹣ ) ,其中 x= +|﹣2|﹣3tan60°.
17.为了启发学生的阅读自觉性,培养学生的学习毅力,学校决定开展“读书月”活动,对学生最喜欢的图书种类
进行了一次抽样调查,所有图书分成五类:艺术、文学、科普、传记、其他.根据调查结果绘制了两幅不完整的
统计图(每位同学必选且只选最喜欢的一类),根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有 名,喜欢“文学”类的学生有 名;
(2)在扇形统计图中“科普”类所对应的圆心角的度数是 °,“其他”类所对应的百分比是 ;
(3)如果要在这五类图书中任选两类进行调查,恰好选到学生最喜欢的“文学”与“科普”的两类图书的概率
是 .
第 4页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
18.图①、图②、图③均是 5×5的正方形网格,每个小正方形的边长均为 1,每个小正方形的顶点称为格点.点
A、B均在格点上,只用无刻度的尺,分别在给定的网格中按下列要求作△ABC,点 C在格点上.
(1)在图①中,△ABC的面积为 ;
(2)在图②中,△ABC的面积为 5;
(3)在图③中,△ABC是面积为 的钝角三角形.
19.为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余
质量 y(克)随时间 x(分钟)变化的数据(0≤x≤20),并分别绘制在直角坐标系中,如图所示.
(1)从 y=ax+21(a≠0),y= (k≠0),y=﹣0.04x2+bx+c中,选择适当的函数模型分别模拟两种场景下 y随
x变化的函数关系,并求出相应的函数表达式;
(2)查阅文献可知,该化学试剂发挥作用的最低质量为 3克.在上述实验中,该化学试剂在哪种场景下发挥作
用的时间更长?
第 5页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
20.学科综合
我们在物理学科中学过:光线从空气射入水中会发生折射现象(如图 1),我们把 n= 称为折射率(其中α
代表入射角,β代表折射角).
观察实验
为了观察光线的折射现象,设计了图 2所示的实验,即通过细管 MN可以看见水底的物块 C,但不在细管 MN所
在直线上,图 3是实验的示意图,四边形 ABFE为矩形,点 A,C,B在同一直线上,测得 BF=12cm,DF=16cm.
(1)求入射角α的度数.
(2)若 BC=7cm,求光线从空气射入水中的折射率 n.(参考数据: , , )
21.综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着
这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
(1)探究一:将车轮设计成等边三角形,转动过程如图 1,设其中心到顶点的距离是 2,以车轮转动一次(以一
个顶点为支点旋转)为例,中心的轨迹是 ,BA=CA=DA=2,圆心角∠BAD=120°.此时中心轨迹最高点
是 C(即 的中点),转动一次前后中心的连线是 BD(水平线),请在图 2中计算 C到 BD的距离 d1.
(2)探究二:将车轮设计成正方形,转动过程如图 3,设其中心到顶点的距离是 2,以车轮转动一次(以一个顶
点为支点旋转)为例,中心的轨迹是 ,BA=CA=DA=2,圆心角∠BAD=90°.此时中心轨迹最高点是 C(即
的中点),转动一次前后中心的连线是 BD(水平线),请在图 4中计算 C到 BD的距离 d2(结果保留根号).
(3)探究三:将车轮设计成正六边形,转动过程如图 5,设其中心到顶点的距离是 2,以车轮转动一次(以一个
顶点为支点旋转)为例,中心的轨迹是 ,圆心角∠BAD= 60° .
此时中心轨迹最高点是 C(即 的中点),转动一次前后中心的连线是 BD(水平线),在图 6中计算 C到 BD的
第 6页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
距离 d3= 2﹣ (结果保留根号).
(4)归纳推理:比较 d1,d2,d3大小: d1>d2>d3 ,按此规律推理,车轮设计成的正多边形边数越多,其
中心轨迹最高点与转动一次前后中心连线(水平线)的距离 越小 (填“越大”或“越小”).
(5)得出结论:将车轮设计成圆形,转动过程如图 7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨
迹最高点与转动前后中心连线(水平线)的距离 d= 0 .这样车辆行驶平稳、没有颠簸感.所以,将车轮设计
成圆形.
22.探究函数 y=﹣2|x|2+4|x|的图象和性质,探究过程如下:
(1)自变量 x的取值范围是全体实数,x与 y的几组对应值列表如下:
x … ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 …
y … ﹣ 0 m 0 2 0 ﹣ …
其中,m= 2 .根据如表数据,在图 1所示的平面直角坐标系中,通过描点画出了函数图象的一部分,请画出
该函数图象的另一部分.观察图象,写出该函数的一条性质;
(2)点 F是函数 y=﹣2|x|2+4|x|图象上的一动点,点 A(2,0),点 B(﹣2,0),当 S△FAB=3时,请直接写出所
有满足条件的点 F的坐标;
(3)在图 2中,当 x在一切实数范围内时,抛物线 y=﹣2x2+4x交 x轴于 O,A两点(点 O在点 A的左边),点
第 7页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
P是点 Q(1,0)关于抛物线顶点的对称点,不平行 y轴的直线 l分别交线段 OP,AP(不含端点)于 M,N两
点.当直线 l与抛物线只有一个公共点时,PM与 PN的和是否为定值?若是,求出此定值;若不是,请说明理
由.
第 8页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
一.选择题(每题 3 分,共 30 分)
1.如图所示的是某用户微信支付情况,﹣100表示的意思是( )
A.发出 100元红包 B.收入 100元
C.余额 100元 D.抢到 100元红包
2.九(1)班选派 4名学生参加演讲比赛,他们的成绩如下:
选手 A B C D 平均成绩 中位数
成绩/分 86 ■ 82 88 85 ■
则如表中被遮盖的两个数据从左到右依次是( )
A.84,86 B.84,85 C.82,86 D.82,87
3.如图是一个正方体的平面展开图,若正方体中相对的面上的数字或代数式的乘积都小于 0,则整数 x的值是( )
A.0 B.1 C.﹣1 D.2
4.下列运算正确的是( )
A.(x+2)2=x2+4 B.a2 a4=a8
C.(2x3)2=4x6 D.2x2+3x2=5x4
5.将一把直尺和一块含 30°和 60°角的三角板 ABC按如图所示的位置放置,如果∠CDE=45°,那么∠BAF的
大小为( )
第 1页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
A.15° B.10° C.20° D.25°
6.中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),
高铁列车在转弯时的曲线起点为 A,曲线终点为 B,过点 A,B的两条切线相交于点 C,列车在从 A到 B行驶的
过程中转角α为 60°.若圆曲线的半径 OA=1.5km,则这段圆曲线 的长为( )
A. B. C. D.
7.如图,在直角坐标系中,菱形 OABC的顶点 A的坐标为(﹣2,0),∠AOC=60°.将菱形 OABC沿 x轴向右平
移 1个单位长度,再沿 y轴向下平移 1个单位长度,得到菱形 O′A′B′C′,其中点 B′的坐标为( )
A.(﹣2, ﹣1) B.(﹣2,1) C.(﹣ ,1) D.(﹣ , ﹣1)
8.下列哪一个是假命题( )
A.五边形外角和为 360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于 y轴的对称点为(﹣3,2)
D.抛物线 y=x2﹣4x+2017对称轴为直线 x=2
9.已知反比例函数 y= (k≠0)在第一象限内的图象与一次函数 y=﹣x+b的图象如图所示,则函数 y=x2﹣bx+k
﹣1的图象可能为( )
第 2页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
A. B. C. D.
10.发动机的曲柄连杆将直线运动转化为圆周运动,图①是发动机的实物剖面图,图②是其示意图,图②中,点
A在直线 l上往复运动,推动点 B做圆周运动形成⊙O,AB与 BO表示曲柄连杆的两直杆,点 C、D是直线 l与
⊙O的交点;当点 A运动到 E时,点 B到达 C;当点 A运动到 F时,点 B到达 D.若 AB=12,OB=5,则下列
结论正确的是( )
① .FC=2 ②.EF=12 ③.当 AB与⊙O相切时,EA=4 ④.当 OB⊥CD时,EA=AF
A.1个 B、2个 C、3个 D、4个
声明:试题解析著作二.填空题(每题 3 分,共 15 分)
11.小明从《红星照耀中国》,《红岩》,《长征》,《钢铁是怎样炼成的》四本书中随机挑选一本,其中拿到《红星照
耀中国》这本书的概率为 .
12.若 a+b=3,ab=﹣1,则代数式 a3b+2a2b2+ab3的值为 ﹣9 .
13.如图,菱形 ABCD的边长为 8,∠A=45°,分别以点 A,D为圆心,大于 AD的长为半径画弧,两弧相交于
M,N两点,直线 MN交 AB于点 E,连接 CE,则 CE的长为 4 .
14.如图,在直角△ABO中,AO= ,AB=1,将△ABO绕点 O顺时针旋转 105°至△A′B′O的位置,点 E
第 3页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
是 OB′的中点,且点 E在反比例函数 y= 的图象上,则 k的值为 .
15.如图,在四边形 ABCD中,∠BCD=90°,对角线 AC,BD相交于点 O.若 AB=AC=5,BC=6,∠ADB=2
∠CBD,则 AD的长为 .
三.解答题(共 55 分)
16.先化简,再求值:( ﹣ ) ,其中 x= +|﹣2|﹣3tan60°.
17.为了启发学生的阅读自觉性,培养学生的学习毅力,学校决定开展“读书月”活动,对学生最喜欢的图书种类
进行了一次抽样调查,所有图书分成五类:艺术、文学、科普、传记、其他.根据调查结果绘制了两幅不完整的
统计图(每位同学必选且只选最喜欢的一类),根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有 名,喜欢“文学”类的学生有 名;
(2)在扇形统计图中“科普”类所对应的圆心角的度数是 °,“其他”类所对应的百分比是 ;
(3)如果要在这五类图书中任选两类进行调查,恰好选到学生最喜欢的“文学”与“科普”的两类图书的概率
是 .
第 4页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
18.图①、图②、图③均是 5×5的正方形网格,每个小正方形的边长均为 1,每个小正方形的顶点称为格点.点
A、B均在格点上,只用无刻度的尺,分别在给定的网格中按下列要求作△ABC,点 C在格点上.
(1)在图①中,△ABC的面积为 ;
(2)在图②中,△ABC的面积为 5;
(3)在图③中,△ABC是面积为 的钝角三角形.
19.为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余
质量 y(克)随时间 x(分钟)变化的数据(0≤x≤20),并分别绘制在直角坐标系中,如图所示.
(1)从 y=ax+21(a≠0),y= (k≠0),y=﹣0.04x2+bx+c中,选择适当的函数模型分别模拟两种场景下 y随
x变化的函数关系,并求出相应的函数表达式;
(2)查阅文献可知,该化学试剂发挥作用的最低质量为 3克.在上述实验中,该化学试剂在哪种场景下发挥作
用的时间更长?
第 5页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
20.学科综合
我们在物理学科中学过:光线从空气射入水中会发生折射现象(如图 1),我们把 n= 称为折射率(其中α
代表入射角,β代表折射角).
观察实验
为了观察光线的折射现象,设计了图 2所示的实验,即通过细管 MN可以看见水底的物块 C,但不在细管 MN所
在直线上,图 3是实验的示意图,四边形 ABFE为矩形,点 A,C,B在同一直线上,测得 BF=12cm,DF=16cm.
(1)求入射角α的度数.
(2)若 BC=7cm,求光线从空气射入水中的折射率 n.(参考数据: , , )
21.综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着
这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
(1)探究一:将车轮设计成等边三角形,转动过程如图 1,设其中心到顶点的距离是 2,以车轮转动一次(以一
个顶点为支点旋转)为例,中心的轨迹是 ,BA=CA=DA=2,圆心角∠BAD=120°.此时中心轨迹最高点
是 C(即 的中点),转动一次前后中心的连线是 BD(水平线),请在图 2中计算 C到 BD的距离 d1.
(2)探究二:将车轮设计成正方形,转动过程如图 3,设其中心到顶点的距离是 2,以车轮转动一次(以一个顶
点为支点旋转)为例,中心的轨迹是 ,BA=CA=DA=2,圆心角∠BAD=90°.此时中心轨迹最高点是 C(即
的中点),转动一次前后中心的连线是 BD(水平线),请在图 4中计算 C到 BD的距离 d2(结果保留根号).
(3)探究三:将车轮设计成正六边形,转动过程如图 5,设其中心到顶点的距离是 2,以车轮转动一次(以一个
顶点为支点旋转)为例,中心的轨迹是 ,圆心角∠BAD= 60° .
此时中心轨迹最高点是 C(即 的中点),转动一次前后中心的连线是 BD(水平线),在图 6中计算 C到 BD的
第 6页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
距离 d3= 2﹣ (结果保留根号).
(4)归纳推理:比较 d1,d2,d3大小: d1>d2>d3 ,按此规律推理,车轮设计成的正多边形边数越多,其
中心轨迹最高点与转动一次前后中心连线(水平线)的距离 越小 (填“越大”或“越小”).
(5)得出结论:将车轮设计成圆形,转动过程如图 7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨
迹最高点与转动前后中心连线(水平线)的距离 d= 0 .这样车辆行驶平稳、没有颠簸感.所以,将车轮设计
成圆形.
22.探究函数 y=﹣2|x|2+4|x|的图象和性质,探究过程如下:
(1)自变量 x的取值范围是全体实数,x与 y的几组对应值列表如下:
x … ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 …
y … ﹣ 0 m 0 2 0 ﹣ …
其中,m= 2 .根据如表数据,在图 1所示的平面直角坐标系中,通过描点画出了函数图象的一部分,请画出
该函数图象的另一部分.观察图象,写出该函数的一条性质;
(2)点 F是函数 y=﹣2|x|2+4|x|图象上的一动点,点 A(2,0),点 B(﹣2,0),当 S△FAB=3时,请直接写出所
有满足条件的点 F的坐标;
(3)在图 2中,当 x在一切实数范围内时,抛物线 y=﹣2x2+4x交 x轴于 O,A两点(点 O在点 A的左边),点
第 7页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
P是点 Q(1,0)关于抛物线顶点的对称点,不平行 y轴的直线 l分别交线段 OP,AP(不含端点)于 M,N两
点.当直线 l与抛物线只有一个公共点时,PM与 PN的和是否为定值?若是,求出此定值;若不是,请说明理
由.
第 8页(共 8页)
{#{QQABKYqAggAIAAIAAAgCEwXaCEGQkAAAAAoGAFAAsAABSRFABAA=}#}
同课章节目录
