7.3图形的平移 同步练习题 苏科版七年级数学下册(含答案解析)
文档属性
| 名称 | 7.3图形的平移 同步练习题 苏科版七年级数学下册(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 877.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 08:15:23 | ||
图片预览


文档简介
苏科版七年级数学下册《7.3图形的平移》同步练习题(附答案)
一、单选题
1.2022年2月4日,第二十四届冬季奥林匹克运动会在北京隆重开幕.此次冬奥会的吉祥物“冰墩墩”是熊猫形象与冰晶外壳相结合,体现了追求卓越、引领时代以及面向未来的无限可能、在下面的四个冰墩墩图片中,能由如图经过平移得到的是( )
A. B. C. D.
2.下列运动属于平移的是( )
A.荡秋千的小朋友 B.转动的电风扇叶片
C.正在上升的电梯 D.行驶的自行车后轮
3.如图所示的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
4.如图,将沿射线平移得到,则下列线段的长度中表示平移距离的是( )
A. B. C. D.
5.如图,将沿方向平移得到,若的周长为,则四边形的周长为( )
A. B. C. D.
6.如图,在长方形长,宽地块内修筑同样宽的两条“之”字路,余下部分作为耕地,道路宽为2米时耕地面积为多少平方米?( )
A.504 B.540 C.560 D.600
7.如图,直角三角形的周长为22,在其内部有5个小直角三角形,这5个小直角三角形都有一条边与平行,则这5个小直角三角形的周长为( )
A.11 B.22 C.33 D.44
8.如图,三角形的边的长为5cm.将三角形向上平移2cm得到三角形,且,则阴影部分的面积为( )
A. B. C. D.
二、填空题
9.已知线段AB=3cm,经过平移,线段AB的端点A移到A1,端点B移到B1,且AA1=5cm,则BB1= cm
10.如图,,直线平移后得到直线,则 .
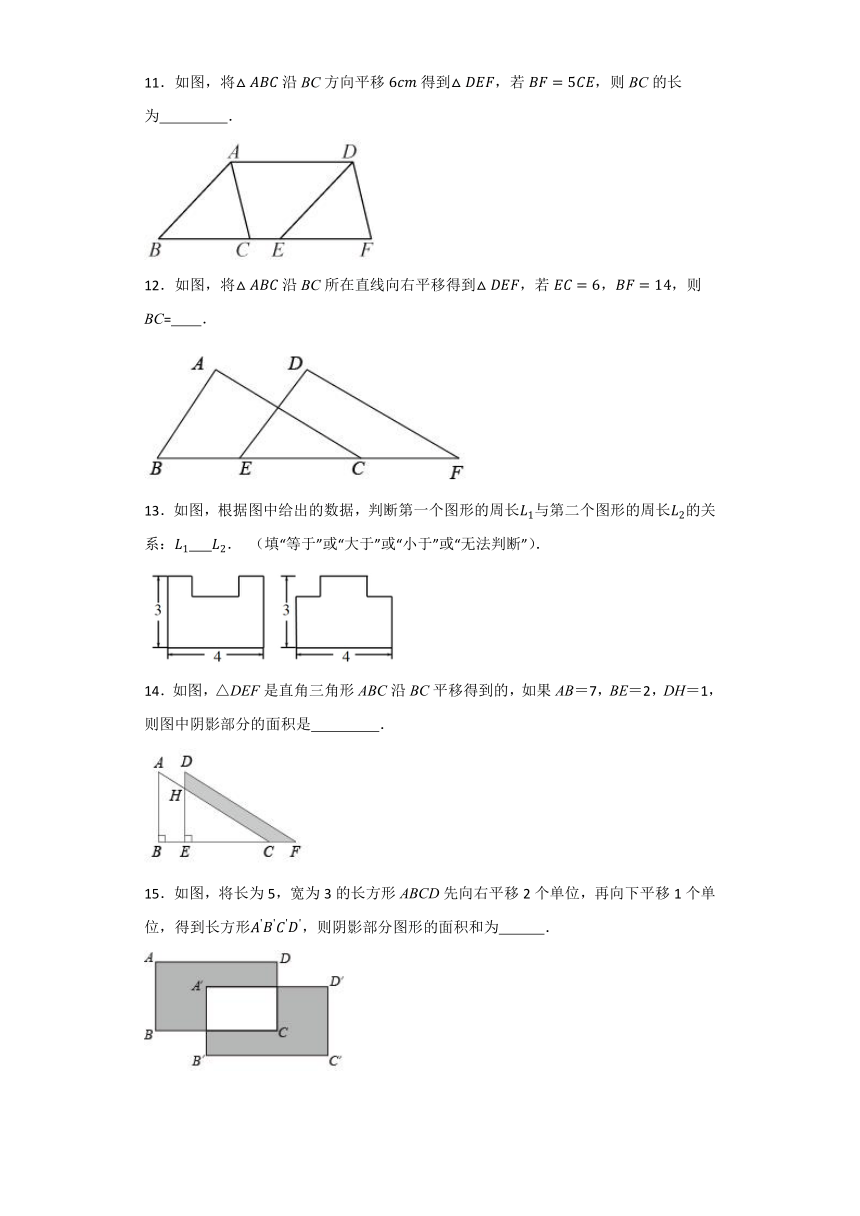
11.如图,将沿BC方向平移得到,若,则BC的长为 .
12.如图,将沿BC所在直线向右平移得到,若,,则BC= .
13.如图,根据图中给出的数据,判断第一个图形的周长与第二个图形的周长的关系: . (填“等于”或“大于”或“小于”或“无法判断”).
14.如图,△DEF是直角三角形ABC沿BC平移得到的,如果AB=7,BE=2,DH=1,则图中阴影部分的面积是 .
15.如图,将长为5,宽为3的长方形ABCD先向右平移2个单位,再向下平移1个单位,得到长方形,则阴影部分图形的面积和为 .
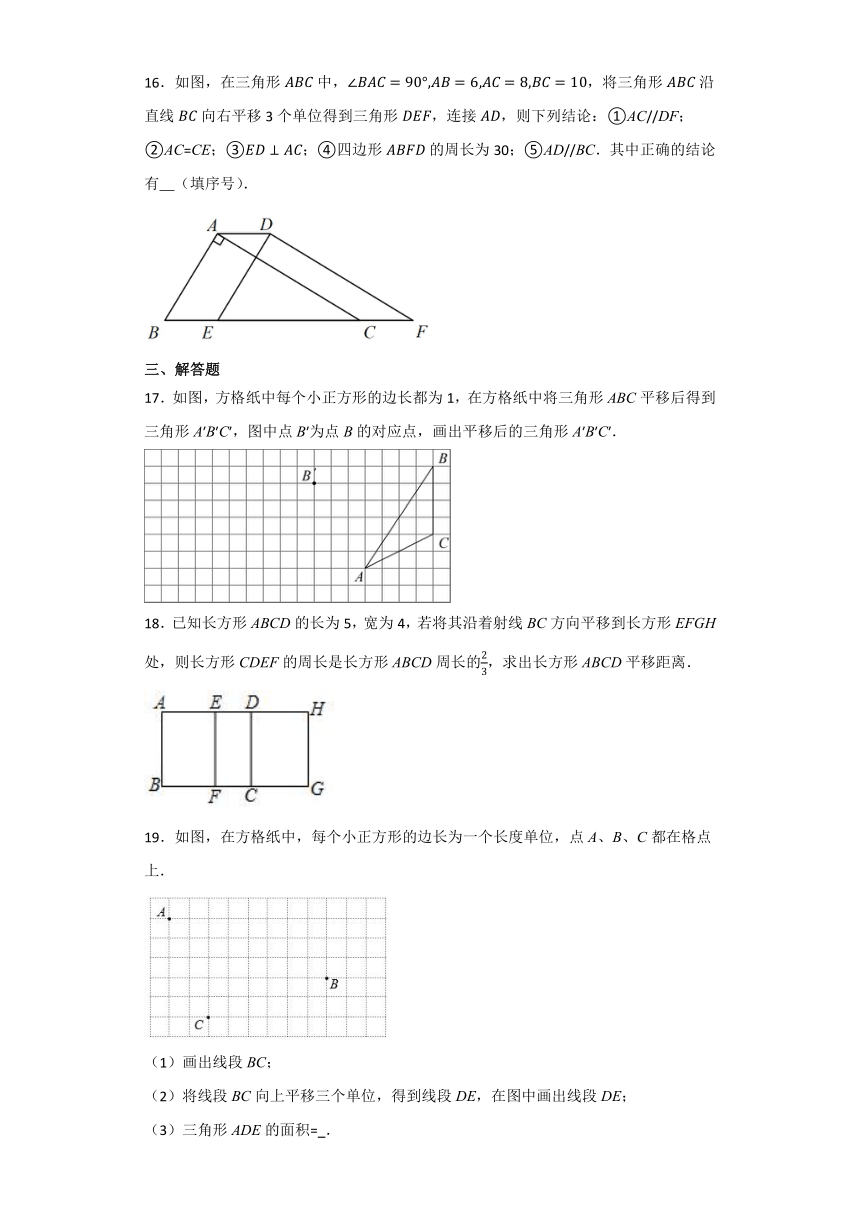
16.如图,在三角形中,,将三角形沿直线向右平移3个单位得到三角形,连接,则下列结论:①AC//DF;②AC=CE;③;④四边形的周长为30;⑤AD//BC.其中正确的结论有 (填序号).
三、解答题
17.如图,方格纸中每个小正方形的边长都为1,在方格纸中将三角形ABC平移后得到三角形A′B′C′,图中点B′为点B的对应点,画出平移后的三角形A′B′C′.
18.已知长方形ABCD的长为5,宽为4,若将其沿着射线BC方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长的,求出长方形ABCD平移距离.
19.如图,在方格纸中,每个小正方形的边长为一个长度单位,点A、B、C都在格点上.
(1)画出线段BC;
(2)将线段BC向上平移三个单位,得到线段DE,在图中画出线段DE;
(3)三角形ADE的面积= .
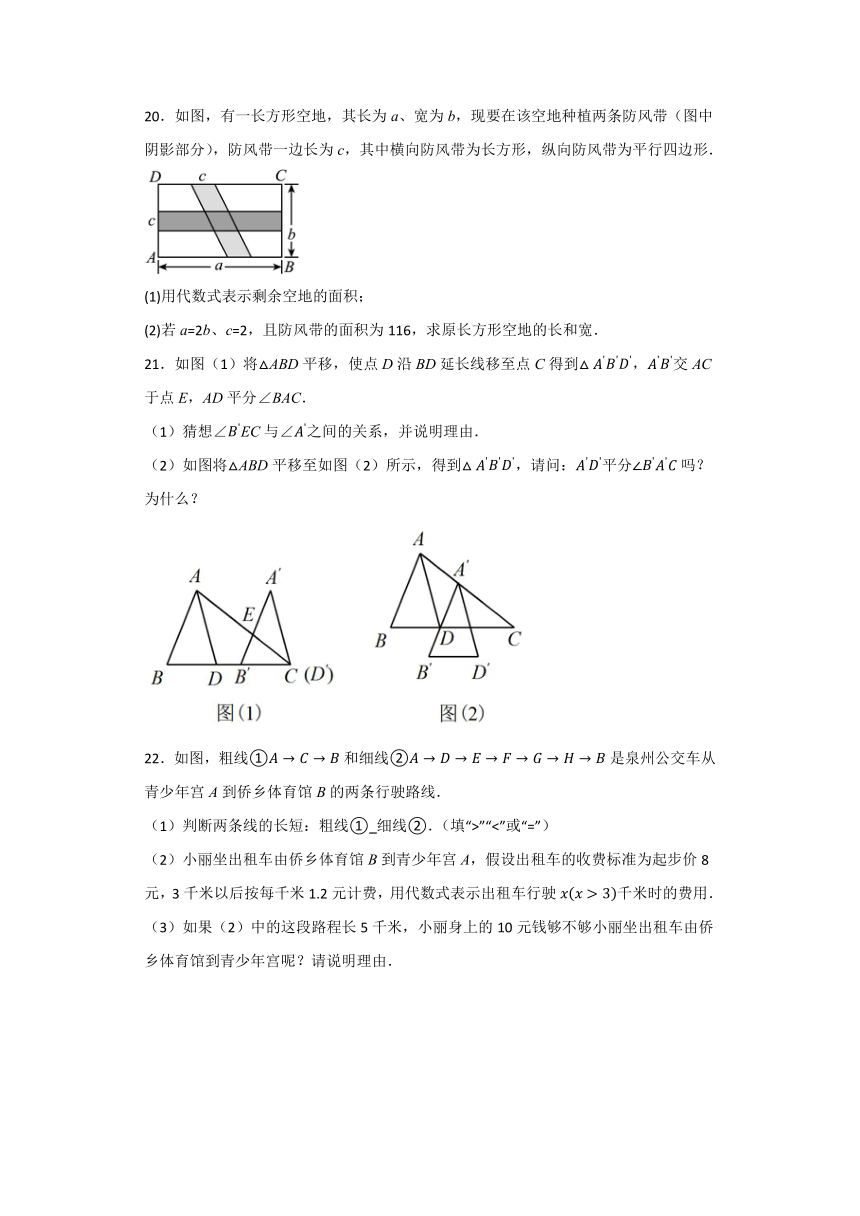
20.如图,有一长方形空地,其长为a、宽为b,现要在该空地种植两条防风带(图中阴影部分),防风带一边长为c,其中横向防风带为长方形,纵向防风带为平行四边形.
(1)用代数式表示剩余空地的面积;
(2)若a=2b、c=2,且防风带的面积为116,求原长方形空地的长和宽.
21.如图(1)将ABD平移,使点D沿BD延长线移至点C得到,交AC于点E,AD平分∠BAC.
(1)猜想∠EC与∠之间的关系,并说明理由.
(2)如图将ABD平移至如图(2)所示,得到,请问:平分吗?为什么?
22.如图,粗线①和细线②是泉州公交车从青少年宫A到侨乡体育馆B的两条行驶路线.
(1)判断两条线的长短:粗线① 细线②.(填“>”“<”或“=”)
(2)小丽坐出租车由侨乡体育馆B到青少年宫A,假设出租车的收费标准为起步价8元,3千米以后按每千米1.2元计费,用代数式表示出租车行驶千米时的费用.
(3)如果(2)中的这段路程长5千米,小丽身上的10元钱够不够小丽坐出租车由侨乡体育馆到青少年宫呢?请说明理由.
23.如图,在9×9的正方形网格中,每个小正方形的边长为1,△ABC的顶点在网格的格点上(小正方形的顶点即为格点),借助网格完成以下任务.
(1)在图中画出△ABC的高AD,中线CE;
(2)将△ABC向右平移1格,再向上平移2格:
①在图中画出平移后的△,并分别标注出点A、B、C的对应点;
②图中,AC与的位置关系是______;
③图中与∠BAC相等的角是______.
参考答案
1.解:根据平移的性质,平移后不改变图形的形状和大小,也不改变图形的方向(角度),符合条件的只有C.
故选C.
2.解:A. 荡秋千的小朋友是旋转,不符合题意;
B. 转动的电风扇叶片是旋转,不符合题意;
C. 正在上升的电梯是平移,符合题意;
D. 行驶的自行车后轮是旋转,不符合题意;
故选C.
3.解:根据平移的概念,观察图形可知图案C通过平移后可以得到.
故选:C.
4.解:∵沿射线平移得到,
∴点与点是对应点,点与点是对应点,
∴线段、可表示平移距离,
故选:C.
5.解:∵将沿方向平移得到,
∴,
∵的周长为,
∴的周长为,
∴四边形的周长,
∵,
∴,
∴四边形的周长,
故选.
6.解:平移后得耕地长为米,宽为米,
∴面积为平方米,
故选:A.
7.解:由题意可知,这5个小直角三角形的周长与大的直角三角形的周长相等.
∴这5个小直角三角形的周长为22.
故选:B.
8.解:三角形的边的长为5cm.将三角形向上平移2cm得到三角形,且,
则:,四边形是长方形,,
∴;
故选B.
9.解:根据新图形与原图形各对应点的连线平行且相等,即可得到结果.
由题意得,BB1=AA1=5cm.
10.解:如图,
∵直线b平移后得到直线a,
∴ab,
∴∠4=∠3=38°,
∵∠2=∠4+∠5,∠5=180°-∠1,
∴∠2=38°+180°-∠1,
∴∠1+∠2=218°.
故答案为:218.
11.解:由平移可得,BE=CF=AD=6cm,
∵BF=BE+EF=6+(CF-CE)=6+6-CE=5CE,
∴CE=2cm,
∴BC=BE-CE=6-2=4cm,
故答案为:4cm.
12.解:由平移的性质可知,EF=BC,
∴EF EC=BC EC,即BE=CF,
∵EC=6,BF=14,
∴BE+CF=14-6=8,
∴BE=CF=4,
BC=BE+EC=4+6=10
故答案为:10.
13.解:如图所示,设凹槽的深度为a,
由题意得,第一个图形的周长,
第二个图形的周长,
∵,
∴,
故答案为:大于.
14.解:由平移的性质知,DE=AB=7,HE=DE-DH=6,CF=BE=2,
HC∥DF,∠DEF=∠B=90°,
又SΔABC=SΔDEF
∴S梯形ABEH+SΔHEC= SΔHEC+ S阴影
∴S阴影= S梯形ABEH
S梯形ABEH =,
S阴影= S梯形ABEH=13,
故答案为13.
15.解:由题意,空白部分是长方形,长为,宽为,
∴阴影部分的面积.
故答案为:18.
16.解:∵将三角形沿直线向右平移3个单位得到三角形,连接,,
∴AC//DF,AD//BC,AB//DE,AC=DF,AD=BE=CF=3,故①⑤正确,
∵BC=10,
∴CE=BC-BE=7,BF=BC+CF=13,
∵AC=8,
∴AC≠CE,故②错误,
∵AB//DE,∠BAC=90°,
∴,故③正确,
∵AB=6,AC=8,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+BF+AC+AD=6+13+8+3=30,故④正确,
综上所述:正确的结论有①③④⑤,
故答案为:①③④⑤
17.解:如图:△A′B′C′即为所求.
18.解:设长方形ABCD平移距离AE=x,
∵长方形ABCD的长为5,宽为4,
∴长方形ABCD的周长=18,
∵长方形CDEF的周长是长方形ABCD周长的,
∴4+4+5﹣x+5﹣x=18×,
∴x=3,
∴长方形ABCD平移距离为3.
19.解:(1)线段BC如图所示,
(2)线段DE如图所示,
(3)三角形ADE的面积=
20.(1)解:由平移,可知
剩余空地面积为(a-c)×(b-c)=ab-ac-bc+c2
答:剩余空地面积为ab-ac-bc+c2.
(2)解:防风带面积为:bc+ac-c2
∵a=2b,c=2,且防风带的面积为116
∴2b+2b×2-4=116
解得b=20
∴a=2×20=40
答:原长方形空地的长为40,宽为20.
21.解:(1)∠B′EC=2∠A′,
理由:
∵将△ABD平移,使点D沿BD延长线移至点C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=∠BAC=∠B′EC,
即∠B′EC=2∠A′.
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移后得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C.
∵∠BAD=∠BAC,
∴∠B′A′D′=∠B′A′C,
∴A′D′平分∠B′A′C.
22.解:(1)如图所示:
∵BH+GF+DE=AC,HG+FE+DA=BC,
∴粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
故答案为:=;
(2)根据题意得:出租车行驶x千米的费用=8+1.2(x﹣3)=(1.2x+4.4)元;
(3)当x=5时,出租车行驶5千米的费用=1.2×5+4.4=10.4>10,
∴小丽身上的钱不够坐出租车由体育馆到少年宫.
23.(1)解:如图所示,线段AD、CE即为所要求作的线段;
(2)解:①如图所示,△即为所要求作的三角形;
②∵△ABC平移得到△,
∴AC ;
故答案为:
③∵△ABC平移得到△,
∴∠BAC=∠,
∵AC ,
∴∠BAC=∠AB′A′.
故答案为:∠,∠A.
一、单选题
1.2022年2月4日,第二十四届冬季奥林匹克运动会在北京隆重开幕.此次冬奥会的吉祥物“冰墩墩”是熊猫形象与冰晶外壳相结合,体现了追求卓越、引领时代以及面向未来的无限可能、在下面的四个冰墩墩图片中,能由如图经过平移得到的是( )
A. B. C. D.
2.下列运动属于平移的是( )
A.荡秋千的小朋友 B.转动的电风扇叶片
C.正在上升的电梯 D.行驶的自行车后轮
3.如图所示的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
4.如图,将沿射线平移得到,则下列线段的长度中表示平移距离的是( )
A. B. C. D.
5.如图,将沿方向平移得到,若的周长为,则四边形的周长为( )
A. B. C. D.
6.如图,在长方形长,宽地块内修筑同样宽的两条“之”字路,余下部分作为耕地,道路宽为2米时耕地面积为多少平方米?( )
A.504 B.540 C.560 D.600
7.如图,直角三角形的周长为22,在其内部有5个小直角三角形,这5个小直角三角形都有一条边与平行,则这5个小直角三角形的周长为( )
A.11 B.22 C.33 D.44
8.如图,三角形的边的长为5cm.将三角形向上平移2cm得到三角形,且,则阴影部分的面积为( )
A. B. C. D.
二、填空题
9.已知线段AB=3cm,经过平移,线段AB的端点A移到A1,端点B移到B1,且AA1=5cm,则BB1= cm
10.如图,,直线平移后得到直线,则 .
11.如图,将沿BC方向平移得到,若,则BC的长为 .
12.如图,将沿BC所在直线向右平移得到,若,,则BC= .
13.如图,根据图中给出的数据,判断第一个图形的周长与第二个图形的周长的关系: . (填“等于”或“大于”或“小于”或“无法判断”).
14.如图,△DEF是直角三角形ABC沿BC平移得到的,如果AB=7,BE=2,DH=1,则图中阴影部分的面积是 .
15.如图,将长为5,宽为3的长方形ABCD先向右平移2个单位,再向下平移1个单位,得到长方形,则阴影部分图形的面积和为 .
16.如图,在三角形中,,将三角形沿直线向右平移3个单位得到三角形,连接,则下列结论:①AC//DF;②AC=CE;③;④四边形的周长为30;⑤AD//BC.其中正确的结论有 (填序号).
三、解答题
17.如图,方格纸中每个小正方形的边长都为1,在方格纸中将三角形ABC平移后得到三角形A′B′C′,图中点B′为点B的对应点,画出平移后的三角形A′B′C′.
18.已知长方形ABCD的长为5,宽为4,若将其沿着射线BC方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长的,求出长方形ABCD平移距离.
19.如图,在方格纸中,每个小正方形的边长为一个长度单位,点A、B、C都在格点上.
(1)画出线段BC;
(2)将线段BC向上平移三个单位,得到线段DE,在图中画出线段DE;
(3)三角形ADE的面积= .
20.如图,有一长方形空地,其长为a、宽为b,现要在该空地种植两条防风带(图中阴影部分),防风带一边长为c,其中横向防风带为长方形,纵向防风带为平行四边形.
(1)用代数式表示剩余空地的面积;
(2)若a=2b、c=2,且防风带的面积为116,求原长方形空地的长和宽.
21.如图(1)将ABD平移,使点D沿BD延长线移至点C得到,交AC于点E,AD平分∠BAC.
(1)猜想∠EC与∠之间的关系,并说明理由.
(2)如图将ABD平移至如图(2)所示,得到,请问:平分吗?为什么?
22.如图,粗线①和细线②是泉州公交车从青少年宫A到侨乡体育馆B的两条行驶路线.
(1)判断两条线的长短:粗线① 细线②.(填“>”“<”或“=”)
(2)小丽坐出租车由侨乡体育馆B到青少年宫A,假设出租车的收费标准为起步价8元,3千米以后按每千米1.2元计费,用代数式表示出租车行驶千米时的费用.
(3)如果(2)中的这段路程长5千米,小丽身上的10元钱够不够小丽坐出租车由侨乡体育馆到青少年宫呢?请说明理由.
23.如图,在9×9的正方形网格中,每个小正方形的边长为1,△ABC的顶点在网格的格点上(小正方形的顶点即为格点),借助网格完成以下任务.
(1)在图中画出△ABC的高AD,中线CE;
(2)将△ABC向右平移1格,再向上平移2格:
①在图中画出平移后的△,并分别标注出点A、B、C的对应点;
②图中,AC与的位置关系是______;
③图中与∠BAC相等的角是______.
参考答案
1.解:根据平移的性质,平移后不改变图形的形状和大小,也不改变图形的方向(角度),符合条件的只有C.
故选C.
2.解:A. 荡秋千的小朋友是旋转,不符合题意;
B. 转动的电风扇叶片是旋转,不符合题意;
C. 正在上升的电梯是平移,符合题意;
D. 行驶的自行车后轮是旋转,不符合题意;
故选C.
3.解:根据平移的概念,观察图形可知图案C通过平移后可以得到.
故选:C.
4.解:∵沿射线平移得到,
∴点与点是对应点,点与点是对应点,
∴线段、可表示平移距离,
故选:C.
5.解:∵将沿方向平移得到,
∴,
∵的周长为,
∴的周长为,
∴四边形的周长,
∵,
∴,
∴四边形的周长,
故选.
6.解:平移后得耕地长为米,宽为米,
∴面积为平方米,
故选:A.
7.解:由题意可知,这5个小直角三角形的周长与大的直角三角形的周长相等.
∴这5个小直角三角形的周长为22.
故选:B.
8.解:三角形的边的长为5cm.将三角形向上平移2cm得到三角形,且,
则:,四边形是长方形,,
∴;
故选B.
9.解:根据新图形与原图形各对应点的连线平行且相等,即可得到结果.
由题意得,BB1=AA1=5cm.
10.解:如图,
∵直线b平移后得到直线a,
∴ab,
∴∠4=∠3=38°,
∵∠2=∠4+∠5,∠5=180°-∠1,
∴∠2=38°+180°-∠1,
∴∠1+∠2=218°.
故答案为:218.
11.解:由平移可得,BE=CF=AD=6cm,
∵BF=BE+EF=6+(CF-CE)=6+6-CE=5CE,
∴CE=2cm,
∴BC=BE-CE=6-2=4cm,
故答案为:4cm.
12.解:由平移的性质可知,EF=BC,
∴EF EC=BC EC,即BE=CF,
∵EC=6,BF=14,
∴BE+CF=14-6=8,
∴BE=CF=4,
BC=BE+EC=4+6=10
故答案为:10.
13.解:如图所示,设凹槽的深度为a,
由题意得,第一个图形的周长,
第二个图形的周长,
∵,
∴,
故答案为:大于.
14.解:由平移的性质知,DE=AB=7,HE=DE-DH=6,CF=BE=2,
HC∥DF,∠DEF=∠B=90°,
又SΔABC=SΔDEF
∴S梯形ABEH+SΔHEC= SΔHEC+ S阴影
∴S阴影= S梯形ABEH
S梯形ABEH =,
S阴影= S梯形ABEH=13,
故答案为13.
15.解:由题意,空白部分是长方形,长为,宽为,
∴阴影部分的面积.
故答案为:18.
16.解:∵将三角形沿直线向右平移3个单位得到三角形,连接,,
∴AC//DF,AD//BC,AB//DE,AC=DF,AD=BE=CF=3,故①⑤正确,
∵BC=10,
∴CE=BC-BE=7,BF=BC+CF=13,
∵AC=8,
∴AC≠CE,故②错误,
∵AB//DE,∠BAC=90°,
∴,故③正确,
∵AB=6,AC=8,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+BF+AC+AD=6+13+8+3=30,故④正确,
综上所述:正确的结论有①③④⑤,
故答案为:①③④⑤
17.解:如图:△A′B′C′即为所求.
18.解:设长方形ABCD平移距离AE=x,
∵长方形ABCD的长为5,宽为4,
∴长方形ABCD的周长=18,
∵长方形CDEF的周长是长方形ABCD周长的,
∴4+4+5﹣x+5﹣x=18×,
∴x=3,
∴长方形ABCD平移距离为3.
19.解:(1)线段BC如图所示,
(2)线段DE如图所示,
(3)三角形ADE的面积=
20.(1)解:由平移,可知
剩余空地面积为(a-c)×(b-c)=ab-ac-bc+c2
答:剩余空地面积为ab-ac-bc+c2.
(2)解:防风带面积为:bc+ac-c2
∵a=2b,c=2,且防风带的面积为116
∴2b+2b×2-4=116
解得b=20
∴a=2×20=40
答:原长方形空地的长为40,宽为20.
21.解:(1)∠B′EC=2∠A′,
理由:
∵将△ABD平移,使点D沿BD延长线移至点C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=∠BAC=∠B′EC,
即∠B′EC=2∠A′.
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移后得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C.
∵∠BAD=∠BAC,
∴∠B′A′D′=∠B′A′C,
∴A′D′平分∠B′A′C.
22.解:(1)如图所示:
∵BH+GF+DE=AC,HG+FE+DA=BC,
∴粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
故答案为:=;
(2)根据题意得:出租车行驶x千米的费用=8+1.2(x﹣3)=(1.2x+4.4)元;
(3)当x=5时,出租车行驶5千米的费用=1.2×5+4.4=10.4>10,
∴小丽身上的钱不够坐出租车由体育馆到少年宫.
23.(1)解:如图所示,线段AD、CE即为所要求作的线段;
(2)解:①如图所示,△即为所要求作的三角形;
②∵△ABC平移得到△,
∴AC ;
故答案为:
③∵△ABC平移得到△,
∴∠BAC=∠,
∵AC ,
∴∠BAC=∠AB′A′.
故答案为:∠,∠A.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
