北师大版六年级下册数学总复习1.11 式与方程课件(共40张PPT)
文档属性
| 名称 | 北师大版六年级下册数学总复习1.11 式与方程课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 08:19:17 | ||
图片预览










文档简介
(共40张PPT)
式与方程
总复习(1)数与代数
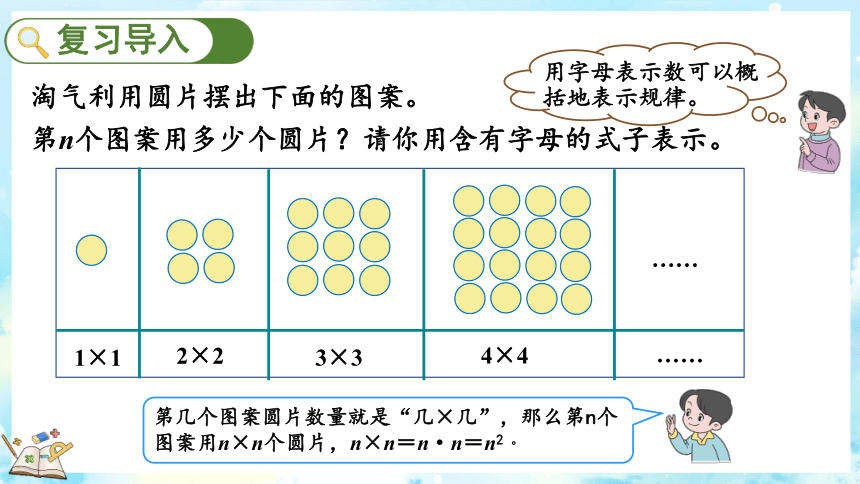
用字母表示数可以概括地表示规律。
1×1
2×2
3×3
4×4
第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2 。
淘气利用圆片摆出下面的图案。
第n个图案用多少个圆片?请你用含有字母的式子表示。
……
……
正方形的面积可以用n2表示:一个边长是n cm的正方形,面积=边长×边长=n×n=n2。
方阵的人数可以用n2表示:一个方阵,每排n人,有n排,那么总人数为n×n=n2。
生活中还有哪些规律能利用n2表示?
梨树棵树=桃树棵树+20棵
根据下面已知条件,找出等量关系。
4.梯形的面积是235平方米。
2.爸爸的年龄是小明的8倍。
1.梨树比桃树多20棵。
3.学校买来6张桌子和12把椅子,共付215.40元。
5.男生人数比女生多20%。
6张桌子总价+12把椅子=总价215.40元
爸爸年龄=小明年龄×8
(上底+下底)× 高÷2=235平方米
男生人数=女生人数×(1+20%)
我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
正方形周长:
C=4a
长方形周长:
C=2(a+b)
S=ah
S=(a+b)h
V=abh
S=a2
S=ab
S=ah
S=2(ab+ah+bh)
S=6a2
平行四边形面积:
梯形面积:
长方体体积:
正方形面积:
长方形面积:
三角形面积:
长方体表面积:
正方体表面积:
圆的周长:
C=2πr=πd
V=a3
S=πr2
正方体体积:
圆柱体积:
圆锥体积:
V=sh
V=h
圆的面积:
a+b = b+a
(a+b)+c = a+(b+c)
(ab)c = a(bc)
(a+b)c=ac+bc
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
ab = ba
a乘4.5可以怎样写?s乘以h可以怎样写?
a·4.5或4.5a
s·h或sh
在一个含有字母的式子里,数字与字母,字母与字母相乘时,乘号可以写作“·”或省略不写,数字写在字母的前面。
含有字母式子的简写
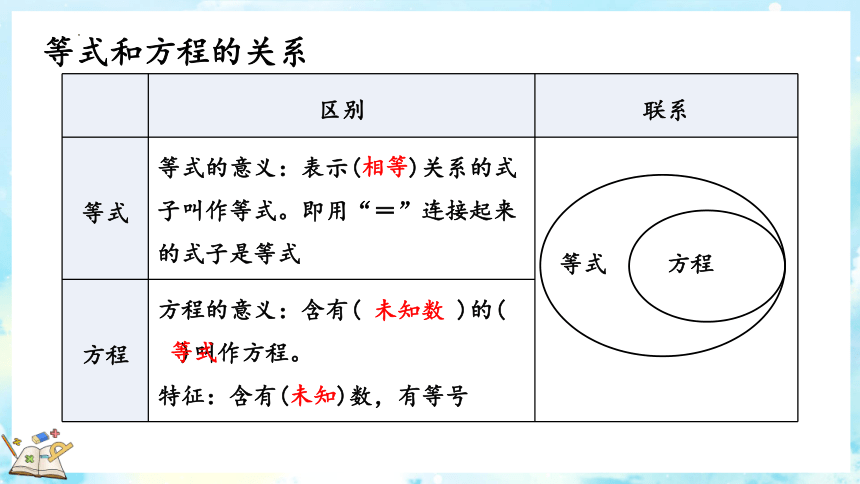
区别 联系
等式 等式的意义:表示( )关系的式子叫作等式。即用“=”连接起来的式子是等式
方程 方程的意义:含有( )的( )叫作方程。 特征:含有( )数,有等号
等式
方程
相等
未知数
等式
未知
等式和方程的关系
不同点
方程的解 使( )左右两边相等的( )的值叫作方程的解。方程的解是一个( )
解方程 求方程的解的( )叫作解方程。解方程是一个过程
方程
未知数
数值
过程
方程的解和解方程
解下面的方程,并说一说你是怎么解的。
解:9x-1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x-1.8=5.4 0.8x+1.2x=25
解:(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
等式的性质
在等式的两边同时加上(或减去)一个相同的数,结果仍是等式。
在等式的两边同时乘(或除以)一个相同的数(零除外),结果仍是等式。
列方程解应用题的步骤:
一般分5步:
(1)根据题意,解设未知数为x 。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程。
(5)检验并答句。
(1)果品商店购进20箱苹果,购进苹果的箱数是橘子箱数的。商店购进了多少箱橘子?
解:设商店购进了x箱橘子。
答:商店购进了25箱橘子。
橘子箱数×=苹果箱数
x=20÷
x=25
x=20
列方程解决下面的问题。
(2)妙想和乐乐一共收集了128枚邮票,妙想收集的邮票数是乐乐的3倍。妙想、乐乐各收集了多少枚邮票?
解:设乐乐收集了x枚邮票,妙想收集了3x枚邮票。
乐乐收集的邮票+妙想收集的邮票=一共收集的邮票
x+3x=128
4x=128
x=128÷4
x=32
妙想:32×3=96(枚)
答:乐乐收集了32枚邮票,妙想收集了96枚邮票。
(3)淘气家和奇思家相距1240m。一天,两人约定在两家之间的路上会合。淘气每分走75m,奇思每分走80m。两人同时从家出发,多长时间后能相遇?
解:设x分钟后能相遇。
淘气走的路程+奇思走的路程=一共的路程
75x+80x=1240
155x=1240
x=1240÷155
x=8
答:8分钟后能相遇。
选自教材第81页总复习第1题
1
填一填。
(1)比x少25的数是 。
(2)n的5倍与m的差是 。
(3)一件衬衫a元,一件毛衣的价格是它的2倍
还多6元,毛衣的价格是 元。
(4)原价a元的产品打八折后的价钱是 元。
x 25
5n m
2a+6
80%a
2
我每时行驶akm。
我每时行驶bkm。
两车分别从A、B两地同时出发,相向而行,经过2.5时相遇。
(1)两地间的距离是多少?
2.5(a+b)
或
2.5a+2.5b
选自教材第81页总复习第2题
巩固练习
(2)当a=45,b=60时,求两地间的距离。
2.5(a+b)=2.5×(45+60)=262.5(km)
答:两地间的距离是262.5km。
选自教材第81页总复习第2题
巩固练习
2
我每时行驶akm。
我每时行驶bkm。
两车分别从A、B两地同时出发,相向而行,经过2.5时相遇。
3
r
·
右图中,图的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
正方形的边长即两条半径的长度。
正方形周长:
C=8r
S=4r
正方形面积:
选自教材第81页总复习第3题
巩固练习
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(1)你发现了什么规律?用含有字母的式子表示
出来。
(2)如果摆100个正方形,需要多少根小棒?
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(1)你发现了什么规律?用含有字母的式子表示
出来。
小棒根数是正方形个数的3倍多1。
用含有字母的式子表示为3n+1。
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(2)如果摆100个正方形,需要多少根小棒?
如果摆100个正方形,需要3×100+1=301根小棒。
5
解方程。
15x=60
x+2x=12.6
40%x=4.2
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
选自教材第81页总复习第5题
巩固练习
12+x=25
2x÷5=15
4x 1.6x=36
解:x=25 12
x=13
解:2x=15×5
2x=75
x=37.5
解:2.4x=36
x=15
5
解方程。
选自教材第81页总复习第5题
巩固练习
原价:x元
优惠:6折
现价:1200元
我一周7天共晨跑4.2km。
奇思平均每天跑skm。
6
看图列出方程,并求出方程的解。
60%x=1200
解:x=1200÷60%
x=2000
答:原价2000元。
7s=4.2
解: s=4.2÷7
s=0.6
答:奇思平均每天跑0.6km。
选自教材第82页总复习第6题
巩固练习
原价:x元
优惠:6折
现价:1200元
我一周7天共晨跑4.2km。
奇思平均每天跑skm。
3x=x+10
解:2x=10
x=5
答:重5g。
3x+x=11.2
解: 4x=11.2
x=2.8
答:一段长为2.8。
6
看图列出方程,并求出方程的解。
选自教材第82页总复习第6题
巩固练习
7
每种丛书有多少本?
解:设每种丛书有x本。
8.2x+6.8x=120
15x=120
x=8
答:每种丛书有8本。
选自教材第82页总复习第7题
巩固练习
8
一个数的5倍再加上5正好是100,这个数是多少?
一个数的8倍与它的的和是66,这个数是多少?
猜一猜。
解:设这个数是x。
5x+5=100
5x=95
x=19
选自教材第82页总复习第8题
答:这个数是19。
巩固练习
8
一个数的5倍再加上5正好是100,这个数是多少?
一个数的8倍与它的的和是66,这个数是多少?
猜一猜。
选自教材第82页总复习第8题
解:设这个数是y。
8y+ y=66
y =66
y=8
答:这个数是8。
巩固练习
9
甲、乙两个工程队同修一条公路,他们从两端同时施工。
(1)甲队每天修am,乙队每天修bm,8天修完。
这条公路长多少米?
8(a+b)
答:这条公路长[8(a+b) ]米 。
选自教材第82页总复习第9题
巩固练习
(2)如果这条公路长3000m,甲队每天修85m,乙队每天修65m,修完这条公路需要几天?
解:设修完这条公路需要x天。
(85+65)x=3000
150x=3000
x=20
答:修完这条公路需要20天。
9
选自教材第82页总复习第9题
巩固练习
10
如图,一个正方形的边长增加它的后,得到的新正方形的周长是48cm,原正方形的边长是多少厘米?
解:设原正方形的边长是x厘米。
答:原正方形的边长是9厘米。
x+x=48÷4
x=12
x=9
选自教材第82页总复习第10题
巩固练习
1.用含有字母的式子表示下面的数量。
1.一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
2.小明今年b岁,再过十年是( )岁。
3.一堆货物x吨,运走24吨,还剩( )吨。
4.水果店有x千克苹果,一共装6箱,平均每箱装( )千克。
100a
b+10
x-24
x÷6
注意:①在含有字母的式子里,数和字母中间的乘号可以写作“ ”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
(1)商店原来有x千克洗衣粉,卖出7袋,每袋54千克,还剩4千克。
(2)学校买了8张办公桌和20把椅子,一共花了1860元。已知每张办公桌120元,每把椅子x元。
2.根据题意列出数量关系和方程式。
原有的质量
-
卖出的质量
=
剩下的质量
x
-
54×7
=
4
8张办公桌总价+20把椅子总价=1860元
8×120 + 20 x =1860
五(1)班有60人,是五(2)班人数的1.2倍。五(2)班有多少人?
3.用方程解决倍数及倍数多少问题。
解:设五(2)班有x人。
1.2 x =60
x =60÷1.2
x =50
答:五(2)班有50人。
两地间的路程是210千米,甲、乙两辆汽车同时从两地相向开出,3.5小时相遇,甲车每小时行28千米。乙车每小时行多少千米?
4.用方程解决相遇问题
解:设乙车速度为x千米/时。
(28+ x )×3.5=210
28+ x =210÷3.5
28+ x =60
答:乙车速度为32千米/时。
速度和×相遇时间=路程
x =32
一个三角形的底边长4.3厘米,面积是17.2平方厘米。它的高是多少厘米?
5.用方程解决几何问题
解:设高为x厘米。
4.3 x ÷2=17.2
x =34.4÷4.3
答:高是8厘米。
三角形面积=底×高÷2
x =8
4.3 x =17.2×2
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
桃树和杏树一共有180棵,桃树和杏树各有多少棵?
6.列方程解决含有两个未知数的问题
桃树棵数+杏树棵数=180
解:设桃树有x棵,杏树有3 x棵。
3 x + x =180
答:桃树有45棵,杏树有135棵。
x =45
4 x =180
3 x =135
7.单位“1”未知时,用方程解决比较简便
金桥镇去年植树3600棵,是今年的,今年植树多少棵?
今年棵数×=去年棵数
单位“1”
解:设今年植树x棵。
x =3600
答:今年植树10800棵。
x =10800
x =3600÷
等式的意义:表示相等关系的式子叫做等式。
方程的意义:
含有未知数的等式叫做方程。
2. 所有的方程都是等式,但等式却不是方程。
式与方程
式与方程
总复习(1)数与代数
用字母表示数可以概括地表示规律。
1×1
2×2
3×3
4×4
第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2 。
淘气利用圆片摆出下面的图案。
第n个图案用多少个圆片?请你用含有字母的式子表示。
……
……
正方形的面积可以用n2表示:一个边长是n cm的正方形,面积=边长×边长=n×n=n2。
方阵的人数可以用n2表示:一个方阵,每排n人,有n排,那么总人数为n×n=n2。
生活中还有哪些规律能利用n2表示?
梨树棵树=桃树棵树+20棵
根据下面已知条件,找出等量关系。
4.梯形的面积是235平方米。
2.爸爸的年龄是小明的8倍。
1.梨树比桃树多20棵。
3.学校买来6张桌子和12把椅子,共付215.40元。
5.男生人数比女生多20%。
6张桌子总价+12把椅子=总价215.40元
爸爸年龄=小明年龄×8
(上底+下底)× 高÷2=235平方米
男生人数=女生人数×(1+20%)
我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
正方形周长:
C=4a
长方形周长:
C=2(a+b)
S=ah
S=(a+b)h
V=abh
S=a2
S=ab
S=ah
S=2(ab+ah+bh)
S=6a2
平行四边形面积:
梯形面积:
长方体体积:
正方形面积:
长方形面积:
三角形面积:
长方体表面积:
正方体表面积:
圆的周长:
C=2πr=πd
V=a3
S=πr2
正方体体积:
圆柱体积:
圆锥体积:
V=sh
V=h
圆的面积:
a+b = b+a
(a+b)+c = a+(b+c)
(ab)c = a(bc)
(a+b)c=ac+bc
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
ab = ba
a乘4.5可以怎样写?s乘以h可以怎样写?
a·4.5或4.5a
s·h或sh
在一个含有字母的式子里,数字与字母,字母与字母相乘时,乘号可以写作“·”或省略不写,数字写在字母的前面。
含有字母式子的简写
区别 联系
等式 等式的意义:表示( )关系的式子叫作等式。即用“=”连接起来的式子是等式
方程 方程的意义:含有( )的( )叫作方程。 特征:含有( )数,有等号
等式
方程
相等
未知数
等式
未知
等式和方程的关系
不同点
方程的解 使( )左右两边相等的( )的值叫作方程的解。方程的解是一个( )
解方程 求方程的解的( )叫作解方程。解方程是一个过程
方程
未知数
数值
过程
方程的解和解方程
解下面的方程,并说一说你是怎么解的。
解:9x-1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x-1.8=5.4 0.8x+1.2x=25
解:(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
等式的性质
在等式的两边同时加上(或减去)一个相同的数,结果仍是等式。
在等式的两边同时乘(或除以)一个相同的数(零除外),结果仍是等式。
列方程解应用题的步骤:
一般分5步:
(1)根据题意,解设未知数为x 。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程。
(5)检验并答句。
(1)果品商店购进20箱苹果,购进苹果的箱数是橘子箱数的。商店购进了多少箱橘子?
解:设商店购进了x箱橘子。
答:商店购进了25箱橘子。
橘子箱数×=苹果箱数
x=20÷
x=25
x=20
列方程解决下面的问题。
(2)妙想和乐乐一共收集了128枚邮票,妙想收集的邮票数是乐乐的3倍。妙想、乐乐各收集了多少枚邮票?
解:设乐乐收集了x枚邮票,妙想收集了3x枚邮票。
乐乐收集的邮票+妙想收集的邮票=一共收集的邮票
x+3x=128
4x=128
x=128÷4
x=32
妙想:32×3=96(枚)
答:乐乐收集了32枚邮票,妙想收集了96枚邮票。
(3)淘气家和奇思家相距1240m。一天,两人约定在两家之间的路上会合。淘气每分走75m,奇思每分走80m。两人同时从家出发,多长时间后能相遇?
解:设x分钟后能相遇。
淘气走的路程+奇思走的路程=一共的路程
75x+80x=1240
155x=1240
x=1240÷155
x=8
答:8分钟后能相遇。
选自教材第81页总复习第1题
1
填一填。
(1)比x少25的数是 。
(2)n的5倍与m的差是 。
(3)一件衬衫a元,一件毛衣的价格是它的2倍
还多6元,毛衣的价格是 元。
(4)原价a元的产品打八折后的价钱是 元。
x 25
5n m
2a+6
80%a
2
我每时行驶akm。
我每时行驶bkm。
两车分别从A、B两地同时出发,相向而行,经过2.5时相遇。
(1)两地间的距离是多少?
2.5(a+b)
或
2.5a+2.5b
选自教材第81页总复习第2题
巩固练习
(2)当a=45,b=60时,求两地间的距离。
2.5(a+b)=2.5×(45+60)=262.5(km)
答:两地间的距离是262.5km。
选自教材第81页总复习第2题
巩固练习
2
我每时行驶akm。
我每时行驶bkm。
两车分别从A、B两地同时出发,相向而行,经过2.5时相遇。
3
r
·
右图中,图的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
正方形的边长即两条半径的长度。
正方形周长:
C=8r
S=4r
正方形面积:
选自教材第81页总复习第3题
巩固练习
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(1)你发现了什么规律?用含有字母的式子表示
出来。
(2)如果摆100个正方形,需要多少根小棒?
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(1)你发现了什么规律?用含有字母的式子表示
出来。
小棒根数是正方形个数的3倍多1。
用含有字母的式子表示为3n+1。
4
摆正方形。
正方形个数
摆成的图形
小棒根数
1
2
3
…
…
…
4根
7根
10根
选自教材第81页总复习第4题
巩固练习
(2)如果摆100个正方形,需要多少根小棒?
如果摆100个正方形,需要3×100+1=301根小棒。
5
解方程。
15x=60
x+2x=12.6
40%x=4.2
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
选自教材第81页总复习第5题
巩固练习
12+x=25
2x÷5=15
4x 1.6x=36
解:x=25 12
x=13
解:2x=15×5
2x=75
x=37.5
解:2.4x=36
x=15
5
解方程。
选自教材第81页总复习第5题
巩固练习
原价:x元
优惠:6折
现价:1200元
我一周7天共晨跑4.2km。
奇思平均每天跑skm。
6
看图列出方程,并求出方程的解。
60%x=1200
解:x=1200÷60%
x=2000
答:原价2000元。
7s=4.2
解: s=4.2÷7
s=0.6
答:奇思平均每天跑0.6km。
选自教材第82页总复习第6题
巩固练习
原价:x元
优惠:6折
现价:1200元
我一周7天共晨跑4.2km。
奇思平均每天跑skm。
3x=x+10
解:2x=10
x=5
答:重5g。
3x+x=11.2
解: 4x=11.2
x=2.8
答:一段长为2.8。
6
看图列出方程,并求出方程的解。
选自教材第82页总复习第6题
巩固练习
7
每种丛书有多少本?
解:设每种丛书有x本。
8.2x+6.8x=120
15x=120
x=8
答:每种丛书有8本。
选自教材第82页总复习第7题
巩固练习
8
一个数的5倍再加上5正好是100,这个数是多少?
一个数的8倍与它的的和是66,这个数是多少?
猜一猜。
解:设这个数是x。
5x+5=100
5x=95
x=19
选自教材第82页总复习第8题
答:这个数是19。
巩固练习
8
一个数的5倍再加上5正好是100,这个数是多少?
一个数的8倍与它的的和是66,这个数是多少?
猜一猜。
选自教材第82页总复习第8题
解:设这个数是y。
8y+ y=66
y =66
y=8
答:这个数是8。
巩固练习
9
甲、乙两个工程队同修一条公路,他们从两端同时施工。
(1)甲队每天修am,乙队每天修bm,8天修完。
这条公路长多少米?
8(a+b)
答:这条公路长[8(a+b) ]米 。
选自教材第82页总复习第9题
巩固练习
(2)如果这条公路长3000m,甲队每天修85m,乙队每天修65m,修完这条公路需要几天?
解:设修完这条公路需要x天。
(85+65)x=3000
150x=3000
x=20
答:修完这条公路需要20天。
9
选自教材第82页总复习第9题
巩固练习
10
如图,一个正方形的边长增加它的后,得到的新正方形的周长是48cm,原正方形的边长是多少厘米?
解:设原正方形的边长是x厘米。
答:原正方形的边长是9厘米。
x+x=48÷4
x=12
x=9
选自教材第82页总复习第10题
巩固练习
1.用含有字母的式子表示下面的数量。
1.一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
2.小明今年b岁,再过十年是( )岁。
3.一堆货物x吨,运走24吨,还剩( )吨。
4.水果店有x千克苹果,一共装6箱,平均每箱装( )千克。
100a
b+10
x-24
x÷6
注意:①在含有字母的式子里,数和字母中间的乘号可以写作“ ”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
(1)商店原来有x千克洗衣粉,卖出7袋,每袋54千克,还剩4千克。
(2)学校买了8张办公桌和20把椅子,一共花了1860元。已知每张办公桌120元,每把椅子x元。
2.根据题意列出数量关系和方程式。
原有的质量
-
卖出的质量
=
剩下的质量
x
-
54×7
=
4
8张办公桌总价+20把椅子总价=1860元
8×120 + 20 x =1860
五(1)班有60人,是五(2)班人数的1.2倍。五(2)班有多少人?
3.用方程解决倍数及倍数多少问题。
解:设五(2)班有x人。
1.2 x =60
x =60÷1.2
x =50
答:五(2)班有50人。
两地间的路程是210千米,甲、乙两辆汽车同时从两地相向开出,3.5小时相遇,甲车每小时行28千米。乙车每小时行多少千米?
4.用方程解决相遇问题
解:设乙车速度为x千米/时。
(28+ x )×3.5=210
28+ x =210÷3.5
28+ x =60
答:乙车速度为32千米/时。
速度和×相遇时间=路程
x =32
一个三角形的底边长4.3厘米,面积是17.2平方厘米。它的高是多少厘米?
5.用方程解决几何问题
解:设高为x厘米。
4.3 x ÷2=17.2
x =34.4÷4.3
答:高是8厘米。
三角形面积=底×高÷2
x =8
4.3 x =17.2×2
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
桃树和杏树一共有180棵,桃树和杏树各有多少棵?
6.列方程解决含有两个未知数的问题
桃树棵数+杏树棵数=180
解:设桃树有x棵,杏树有3 x棵。
3 x + x =180
答:桃树有45棵,杏树有135棵。
x =45
4 x =180
3 x =135
7.单位“1”未知时,用方程解决比较简便
金桥镇去年植树3600棵,是今年的,今年植树多少棵?
今年棵数×=去年棵数
单位“1”
解:设今年植树x棵。
x =3600
答:今年植树10800棵。
x =10800
x =3600÷
等式的意义:表示相等关系的式子叫做等式。
方程的意义:
含有未知数的等式叫做方程。
2. 所有的方程都是等式,但等式却不是方程。
式与方程
