六年级下册数学北师大版总复习1.12 正比例与反比例(课件)(共25张PPT)
文档属性
| 名称 | 六年级下册数学北师大版总复习1.12 正比例与反比例(课件)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 08:21:50 | ||
图片预览







文档简介
(共25张PPT)
正比例与反比例
总复习(1)数与代数
举例说明什么是比,什么是比例,以及它们的应用。
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
填一填,并说一说比、分数、除法之间的联系。
3:5==( )÷( )
a:b==( )÷( )
(b≠0)
3
5
3
5
a
b
a
b
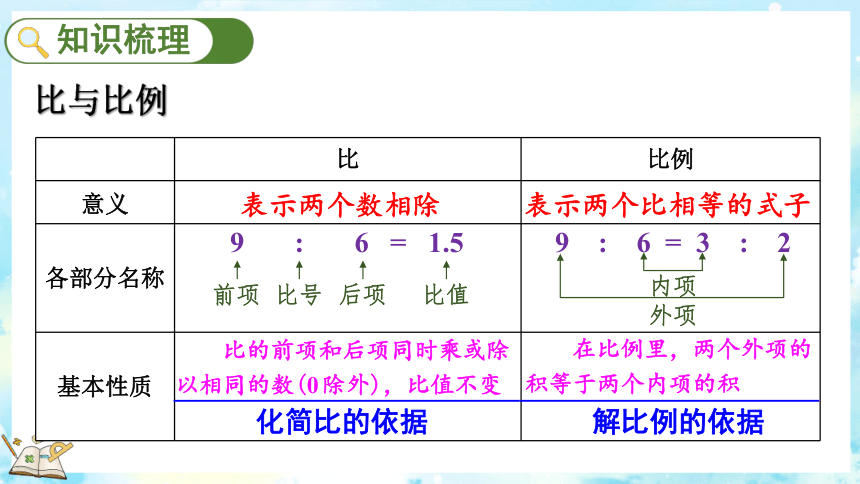
比与比例
比 比例
意义
各部分名称
基本性质
表示两个数相除
表示两个比相等的式子
9 : 6 = 1.5
前项
比号
后项
比值
9 : 6 = 3 : 2
内项
外项
比的前项和后项同时乘或除
以相同的数(0除外),比值不变
在比例里,两个外项的
积等于两个内项的积
化简比的依据
解比例的依据
比、分数、除法之间的关系
联系 例子
各部分名称
分数 分子 分数线 分母 分数值
除法
比
被除数
除号
除数
商
前项
比号
后项
比值
5:8
5÷8=0.625
分数是一种数。除法是数与数之间的运算。比是一种关系。
(1)说说图中的比例尺1:6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,
它的实际占地面积是多少平方米?
图上距离1cm表示实际距离6000cm,即是60m。
240m=24000cm
24000×=4(cm)
答:图上应画4cm。
答:实地占地面积为1800平方米。
1÷=6000(cm)=60(m)
0.5÷=3000(cm)=30(m)
60×30=1800(m )
1. 比例尺=图上距离:实际距离。如图中的比例
尺是1:6000。
图上距离=实际距离×比例尺
3. 实际距离=图上距离÷比例尺
举例说说生活中有哪些成正比例的量,有哪些成反比例的量。
两种相关联的量,一种量变化,另一种量也随
着变化,如果这两种量中相对应的两个数的比值一
定,这种量就叫做
如果这两种量中相对应的两个数的乘积一定,
这种量就叫做
正比例关系。
反比例关系。
工作效率一定,工作时间与工作总量成正比例。
速度一定,时间与路程成正比例。
路程一定,时间和速度成反比例。
总价一定,单价和数量成反比例。
判断正、反比例的方法
一找二看三判断:
找变量:分析数量关系,确定哪两种量是相关
联的量;
看定量:分析这两种量,看它们之间的关系是
商一定还是积一定;
判断:如果商一定,就是正比例;如果积一定,
就是反比例;如果积和商都不是定量,
就不成比例。
一辆汽车在高速路上行驶、速度保持在100千米/时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
(1)可以列表。
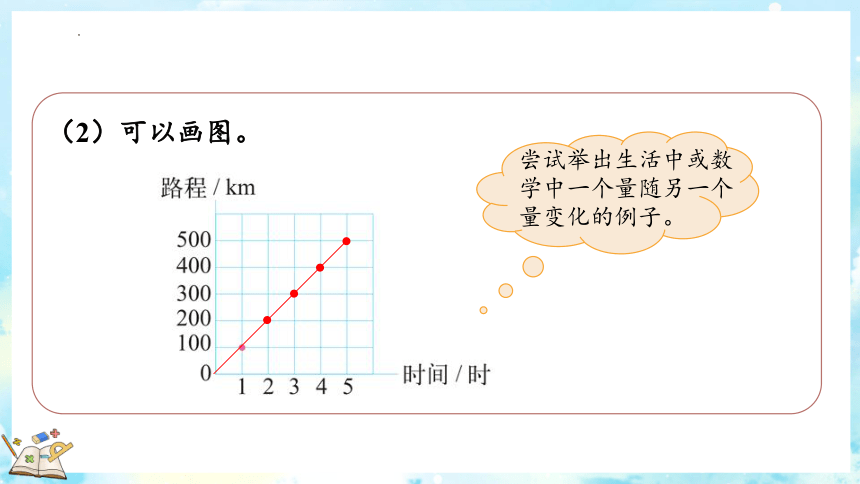
200
300
400
500
时间/时 1 2 3 4 5 ……
路程/km 100
……
(2)可以画图。
尝试举出生活中或数学中一个量随另一个量变化的例子。
(3)可以用式子表示。
如果用t表示汽车的行驶的时间,s表示汽车行驶的路程,那么:
(4)判断路程与时间是否成正比例,说说你是怎么想的。
s÷t=100
路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与时间的比值是一定的,都是100。
选自教材第84页总复习第1题
1
填一填。
(1)两个正方形的边长比是1:3,周长比是
( ),面积比是( )
(2)9元可以买2kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
50:1
50
选自教材第84页总复习第2题
2
化简。
30:120
1:
: 0.1
: 10
= 1∶4
= 4∶3
= 6∶1
= 1∶15
2.5:6
0.5:3.2
25 :
:
= 5∶12
= 5∶32
= 30∶1
= 1∶2
选自教材第84页总复习第3题
3
(1)量一量艺术小学平面图的长是 cm,宽是 cm,这所小学实际占地面积是 m 。
(2)绕操场跑一圈大约是 m,花坛的占地面积是 m 。
(3)教学楼的占地面积是 m ,是学校占地面积的 %。
14
5
28000
240
1256
4200
15
选自教材第84页总复习第4题
4
解方程。
6:0.5=x:
2.8︰x=2︰2.5
解:2x=2.8×2.5
2x=7
x=
3.5
0.5x=4
x=8
解:4x=5
x=
1.25
解:0.5x=6×
=
选自教材第84页总复习第5题
5
判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
答:不成比例。
答:成反比例。
答:成反比例。
选自教材第85页总复习第6题
6
下面表格中的两个量是否成正比例或反比例?为什么?
答:成反比例。因为每分滴数和时间的积一定。
答:不成比例。因为身高与体重无论是积还是商都不一定。
答:成反比例。因为底面积与高的乘积一定。
(1)输液时,一小瓶葡萄糖液均匀滴落,每分滴数与所需时间的关系如下。
每分滴数/滴 60 50 40 30 ……
时间/分 20 24 30 40 ……
(2)妙想的身高与体重的关系如下。
身高/cm 100 110 120 130 ……
体重/kg 17 20 25 31 ……
(3)体积一定,圆柱体的底面积与高的关系如下。
底面积/dm 300 200 150 120 100 ……
高/dm 2 3 4 5 6 ……
选自教材第85页总复习第7题
7
磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/km 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7 km。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗
(3)列车运行2.5分时,行驶的路程是多少
在
(3)解:设列车运行2.5分时,行驶的路程是xkm
=
x=17.5
答:行驶的路程是17.5km。
选自教材第85页总复习第8题
8
育才小学六年级同学从学校出发,乘车0.5时,来到离学校5km的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校。下面三幅图中,哪幅图描述了他们的这一活动行程呢?选一选。
√
(1) 5xy = 20
1.判断下面式子中的x和y成什么比例?
(4) 4x + y = 20
(6) 2x - 3y = 0
(2) 6x =
(3) =
(5) = 20
成正比例
成反比例
不成比例
成反比例
成正比例
成正比例
深色:淡色=20:40=1:2
深色:15÷3×1=5(平方米)
2.一个房间的地面由两种颜色的地砖铺成。
(1)写出两种地砖铺地面积的比,并化简。
(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?
淡色: 15÷3×2=10(平方米)
3.比一比,想一想,列比例求解。
(1)王师傅加工一批机器零件,4分钟加工60个。照这样计算,8分钟加工个。
每分钟加工零件的数量一定,加工总量和加工时间成正比例。
(2)王师傅加工一批机器零件,每小时加工60个,要8小时完成;如果每小时加工80个,要小时完成。
=
加工总量一定,每分钟加工零件的数量和加工时间成反比例。
60×8=80
4.修一条公路,总长12千米,开工3天修了1.5千米。
照这样计算,修完这条路要多少天?
解:设修完这条公路要x天。
=24
答:修完这条路要24天。
3天
1.5千米
x天
12千米
工作效率一定,工作总量和时间成正比例
=
5.大齿轮与小齿轮的齿数比为4∶3。大齿轮有36个齿,小齿轮有多少个齿?
解:设小齿轮有个齿。
4∶3 =36 ∶
=27
答:小齿轮有27个齿。
6.一个比例的两个内项都是质数,它们的积是10,一个外项是0.4,这个比例是多少
解:设一个外项是。
=25
0.4 =2 ×5
:2 =5:0.4
积是10的两个数并且
又是质数的是2和5。
这个比例式是:25∶2=5∶0.4。
一找二看三判断
找变量:分析数量关系,确定哪两种量是相关联的量;
看定量:分析这两种量,看它们之间的关系是商一定还是积一定;
判断:如果商一定,就是正比例;如果积一定,就是反比例;如果积和商都不是定量,就不成比例。
正比例和反比例
正比例与反比例
总复习(1)数与代数
举例说明什么是比,什么是比例,以及它们的应用。
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
填一填,并说一说比、分数、除法之间的联系。
3:5==( )÷( )
a:b==( )÷( )
(b≠0)
3
5
3
5
a
b
a
b
比与比例
比 比例
意义
各部分名称
基本性质
表示两个数相除
表示两个比相等的式子
9 : 6 = 1.5
前项
比号
后项
比值
9 : 6 = 3 : 2
内项
外项
比的前项和后项同时乘或除
以相同的数(0除外),比值不变
在比例里,两个外项的
积等于两个内项的积
化简比的依据
解比例的依据
比、分数、除法之间的关系
联系 例子
各部分名称
分数 分子 分数线 分母 分数值
除法
比
被除数
除号
除数
商
前项
比号
后项
比值
5:8
5÷8=0.625
分数是一种数。除法是数与数之间的运算。比是一种关系。
(1)说说图中的比例尺1:6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,
它的实际占地面积是多少平方米?
图上距离1cm表示实际距离6000cm,即是60m。
240m=24000cm
24000×=4(cm)
答:图上应画4cm。
答:实地占地面积为1800平方米。
1÷=6000(cm)=60(m)
0.5÷=3000(cm)=30(m)
60×30=1800(m )
1. 比例尺=图上距离:实际距离。如图中的比例
尺是1:6000。
图上距离=实际距离×比例尺
3. 实际距离=图上距离÷比例尺
举例说说生活中有哪些成正比例的量,有哪些成反比例的量。
两种相关联的量,一种量变化,另一种量也随
着变化,如果这两种量中相对应的两个数的比值一
定,这种量就叫做
如果这两种量中相对应的两个数的乘积一定,
这种量就叫做
正比例关系。
反比例关系。
工作效率一定,工作时间与工作总量成正比例。
速度一定,时间与路程成正比例。
路程一定,时间和速度成反比例。
总价一定,单价和数量成反比例。
判断正、反比例的方法
一找二看三判断:
找变量:分析数量关系,确定哪两种量是相关
联的量;
看定量:分析这两种量,看它们之间的关系是
商一定还是积一定;
判断:如果商一定,就是正比例;如果积一定,
就是反比例;如果积和商都不是定量,
就不成比例。
一辆汽车在高速路上行驶、速度保持在100千米/时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
(1)可以列表。
200
300
400
500
时间/时 1 2 3 4 5 ……
路程/km 100
……
(2)可以画图。
尝试举出生活中或数学中一个量随另一个量变化的例子。
(3)可以用式子表示。
如果用t表示汽车的行驶的时间,s表示汽车行驶的路程,那么:
(4)判断路程与时间是否成正比例,说说你是怎么想的。
s÷t=100
路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与时间的比值是一定的,都是100。
选自教材第84页总复习第1题
1
填一填。
(1)两个正方形的边长比是1:3,周长比是
( ),面积比是( )
(2)9元可以买2kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
50:1
50
选自教材第84页总复习第2题
2
化简。
30:120
1:
: 0.1
: 10
= 1∶4
= 4∶3
= 6∶1
= 1∶15
2.5:6
0.5:3.2
25 :
:
= 5∶12
= 5∶32
= 30∶1
= 1∶2
选自教材第84页总复习第3题
3
(1)量一量艺术小学平面图的长是 cm,宽是 cm,这所小学实际占地面积是 m 。
(2)绕操场跑一圈大约是 m,花坛的占地面积是 m 。
(3)教学楼的占地面积是 m ,是学校占地面积的 %。
14
5
28000
240
1256
4200
15
选自教材第84页总复习第4题
4
解方程。
6:0.5=x:
2.8︰x=2︰2.5
解:2x=2.8×2.5
2x=7
x=
3.5
0.5x=4
x=8
解:4x=5
x=
1.25
解:0.5x=6×
=
选自教材第84页总复习第5题
5
判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
答:不成比例。
答:成反比例。
答:成反比例。
选自教材第85页总复习第6题
6
下面表格中的两个量是否成正比例或反比例?为什么?
答:成反比例。因为每分滴数和时间的积一定。
答:不成比例。因为身高与体重无论是积还是商都不一定。
答:成反比例。因为底面积与高的乘积一定。
(1)输液时,一小瓶葡萄糖液均匀滴落,每分滴数与所需时间的关系如下。
每分滴数/滴 60 50 40 30 ……
时间/分 20 24 30 40 ……
(2)妙想的身高与体重的关系如下。
身高/cm 100 110 120 130 ……
体重/kg 17 20 25 31 ……
(3)体积一定,圆柱体的底面积与高的关系如下。
底面积/dm 300 200 150 120 100 ……
高/dm 2 3 4 5 6 ……
选自教材第85页总复习第7题
7
磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/km 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7 km。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗
(3)列车运行2.5分时,行驶的路程是多少
在
(3)解:设列车运行2.5分时,行驶的路程是xkm
=
x=17.5
答:行驶的路程是17.5km。
选自教材第85页总复习第8题
8
育才小学六年级同学从学校出发,乘车0.5时,来到离学校5km的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校。下面三幅图中,哪幅图描述了他们的这一活动行程呢?选一选。
√
(1) 5xy = 20
1.判断下面式子中的x和y成什么比例?
(4) 4x + y = 20
(6) 2x - 3y = 0
(2) 6x =
(3) =
(5) = 20
成正比例
成反比例
不成比例
成反比例
成正比例
成正比例
深色:淡色=20:40=1:2
深色:15÷3×1=5(平方米)
2.一个房间的地面由两种颜色的地砖铺成。
(1)写出两种地砖铺地面积的比,并化简。
(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?
淡色: 15÷3×2=10(平方米)
3.比一比,想一想,列比例求解。
(1)王师傅加工一批机器零件,4分钟加工60个。照这样计算,8分钟加工个。
每分钟加工零件的数量一定,加工总量和加工时间成正比例。
(2)王师傅加工一批机器零件,每小时加工60个,要8小时完成;如果每小时加工80个,要小时完成。
=
加工总量一定,每分钟加工零件的数量和加工时间成反比例。
60×8=80
4.修一条公路,总长12千米,开工3天修了1.5千米。
照这样计算,修完这条路要多少天?
解:设修完这条公路要x天。
=24
答:修完这条路要24天。
3天
1.5千米
x天
12千米
工作效率一定,工作总量和时间成正比例
=
5.大齿轮与小齿轮的齿数比为4∶3。大齿轮有36个齿,小齿轮有多少个齿?
解:设小齿轮有个齿。
4∶3 =36 ∶
=27
答:小齿轮有27个齿。
6.一个比例的两个内项都是质数,它们的积是10,一个外项是0.4,这个比例是多少
解:设一个外项是。
=25
0.4 =2 ×5
:2 =5:0.4
积是10的两个数并且
又是质数的是2和5。
这个比例式是:25∶2=5∶0.4。
一找二看三判断
找变量:分析数量关系,确定哪两种量是相关联的量;
看定量:分析这两种量,看它们之间的关系是商一定还是积一定;
判断:如果商一定,就是正比例;如果积一定,就是反比例;如果积和商都不是定量,就不成比例。
正比例和反比例
