高一物理必修二6.4 生活中的圆周运动 专题练习(含答案)
文档属性
| 名称 | 高一物理必修二6.4 生活中的圆周运动 专题练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 761.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览



文档简介
高一物理必修二6.4《生活中的圆周运动》专题练习
(绳模型、管道模型)
一、绳模型
1.飞飞老师心灵手巧,用生活中常见的细绳和塑料容器制作“水流星”模型。如图所示,球形容器中盛有质量为m的清水,然后使其在竖直平面内做半径为L的圆周运动(不考虑细绳和容器质量,重力加速度为g)。则下列说法正确的是( )
A.“水流星”通过最高点时,绳子张力不可以为零
B.“水流星”通过最高点时,清水恰好不流出来的速度是0
C.假如“水流星”可在竖直面内做匀速圆周运动,则“水流星”通过最低点和最高点,细绳的张力差为
D.假如“水流星”可在竖直面内做匀速圆周运动,则“水流星”通过最低点和最高点,细绳的张力差为
2.如图所示,细绳的一端固定于O点,另一端系一个小球,在O点的正下方钉一个钉子P,小球从左侧一定高度摆下(整个过程无能量损失)。已知小球经过最低点时,速度大小不变,则下列说法中正确的是( )
A.在摆动过程中,小球所受重力和绳子拉力的合力始终等于向心力
B.小球经过最低点时,加速度不变
C.钉子位置离O点越远,绳就越容易断
D.钉子位置离O点越近,绳就越容易断
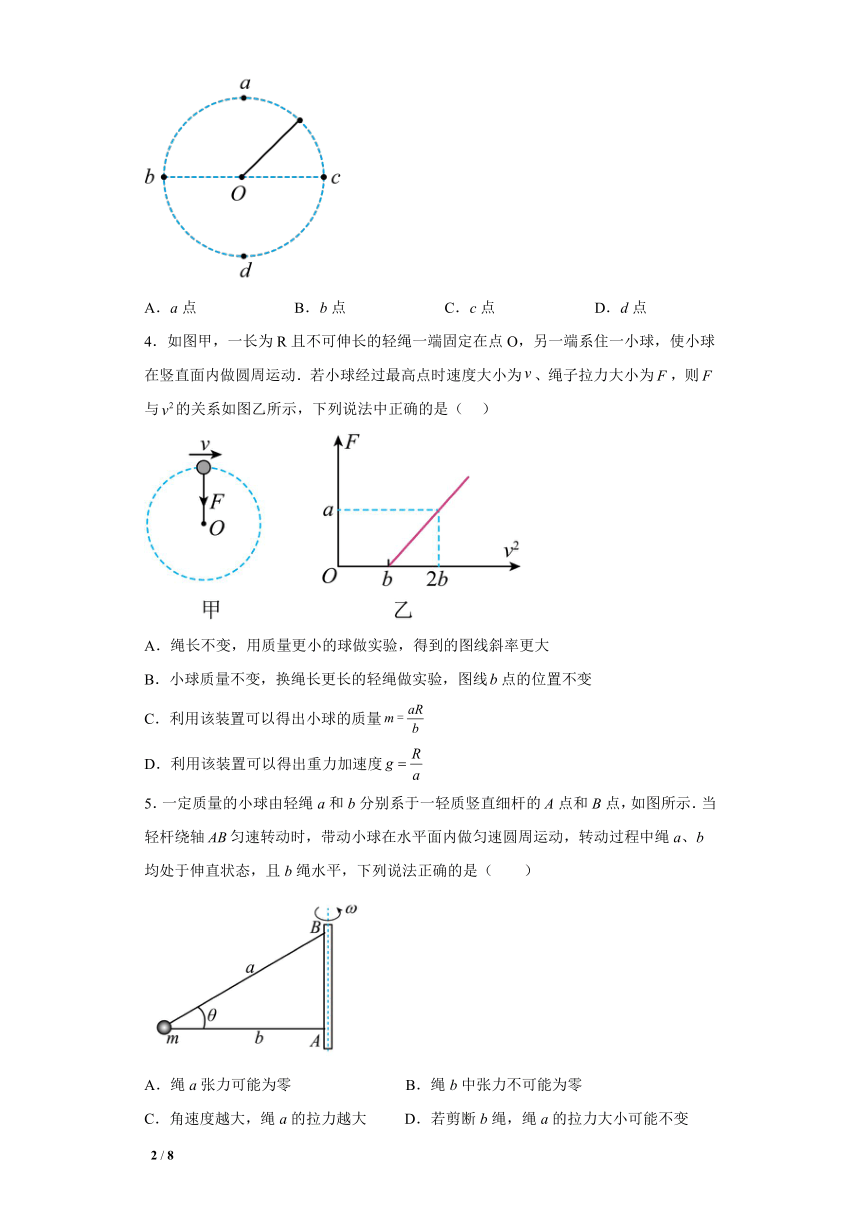
3.如图所示,一根不可伸长的轻绳一端固定在O点,另一端拴一小球在竖直面内做圆周运动,a、b、c、d为其运动轨迹上的四个点,其中a为最高点,d为最低点,b、c两点的连线为圆周的水平直径,不计空气阻力,则在小球做圆周运动的过程中,轻绳对小球的拉力可能为零的位置是( )
A.a点 B.b点 C.c点 D.d点
4.如图甲,一长为R且不可伸长的轻绳一端固定在点O,另一端系住一小球,使小球在竖直面内做圆周运动.若小球经过最高点时速度大小为、绳子拉力大小为,则与的关系如图乙所示,下列说法中正确的是( )
A.绳长不变,用质量更小的球做实验,得到的图线斜率更大
B.小球质量不变,换绳长更长的轻绳做实验,图线点的位置不变
C.利用该装置可以得出小球的质量
D.利用该装置可以得出重力加速度
5.一定质量的小球由轻绳a和b分别系于一轻质竖直细杆的A点和B点,如图所示.当轻杆绕轴匀速转动时,带动小球在水平面内做匀速圆周运动,转动过程中绳a、b均处于伸直状态,且b绳水平,下列说法正确的是( )
A.绳a张力可能为零 B.绳b中张力不可能为零
C.角速度越大,绳a的拉力越大 D.若剪断b绳,绳a的拉力大小可能不变
6.如图,长为的细绳一端拴一质量为的小球,另一端固定在点。现使小球在竖直平面内做完整的圆周运动,转轴离地高,绳所能承受的最大张力为。
(1)求小球通过最高点时最小速度的大小;
(2)分析小球在何位置绳最易被拉断 求出在此位置绳恰被拉断时小球的角速度大小;
(3)在(2)的情况下,求小球落地点距转轴的水平距离及落地速度的大小和方向。
7.如图所示,用长度的轻绳,拴着一质量的小球(视为质点)在竖直面内做圆周运动,已知绳子能够承受的最大张力,圆心O离水平地面的高度,小球在最低点时轻绳恰好断开,不计空气阻力,取重力加速度大小,求:
(1)绳断时小球的线速度大小;
(2)绳断后小球的落地点与绳断时小球所在位置间的水平距离。
(3)小球落地的速度大小及落地速度与水平地面的夹角。
二、管道模型
8.如图所示,过山车的轨道可视为竖直平面内半径为的圆轨道。质量为的游客随过山车一起运动,当游客以速度经过圆轨道最高点时( )
A.处于超重状态 B.加速度方向竖直向下
C.速度大小一定为 D.对座椅的作用力为
9.滚筒洗衣机静止于水平地面上,已脱净水的衣物随滚筒一起在竖直平面内做匀速圆周运动,滚筒截面如图所示。若质量为m的衣物在最高点A对滚筒恰好无作用力,重力加速度大小为g,则衣物在最低点B对滚筒的压力大小为( )
A.mg B.2mg C.3mg D.4mg
10.如图所示,光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知小球在最低点时对轨道的压力大小为N1,速度大小为v1,在最高点时对轨道的压力大小为N2,速度大小为v2,重力加速度大小为g,且v1、v2满足关系式,则N1-N2的值为( )
A.3mg B.4mg C.5mg D.6mg
11.如图质量为m的小球在竖直平面内的光滑圆轨道内做圆周运动。圆轨道半径为R。小球经过最高点时刚好不脱离圆轨道。则其通过最高点时,以下说法正确的是( )
A.小球对圆环的压力大小等于mg B.小球受到的向心力与重力等大反向
C.小球的线速度大小等于 D.小球的向心加速度大小等于g
12.甲图是质量为m的小球,在竖直平面内绕O点做半径为R的圆周运动(OA为细绳);乙图是质量为m的小球,在竖直平面内绕O点做半径为R的圆周运动(OB为轻质杆);丙图是质量为m的小球,在半径为R的竖直光滑圆轨道内侧做圆周运动;丁图是质量为m的小球在竖直放置的半径为R的光滑圆形管道内做圆周运动。则下列说法正确的是( )
A.甲丙图中,小球通过最高点的最小速度都是
B.乙丁图中,小球通过最高点的最小速度都是
C.在丁图中,小球在水平线ab以下管道中运动时,外侧管壁对小球一定无作用力
D.在丁图中,小球在水平线ab以上管道中运动时,内侧管壁对小球一定有作用力
13.如图所示,AB为竖直光滑圆弧的直径,其半径R=0.9m,A端沿水平方向。水平轨道BC与半径r=0.9m的光滑圆弧轨道CD相接于C点,D为圆轨道的最低点,圆弧轨道CD、DE对应的圆心角θ=37°。一质量为M=0.9kg的物块(视为质点)从水平轨道上某点以某一速度冲上竖直圆轨道,并从A点飞出,经过C点恰好沿切线进入圆弧轨道,取g=10m/s ,sin37°=0.6,cos37°=0.8。求:
(1)物块到达C点时的速度大小;
(2)在A点受到的弹力大小FA;
(3)物体对C点的压力大小FC;
14.如图所示,摩托车做腾跃特技表演,沿曲面冲上高顶部水平高台,接着以水平速度离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑。A、B为圆弧两端点,其连线水平。已知圆弧半径为,圆弧所对应圆心角,人和车的总质量为,特技表演的全过程中,空气阻力忽略不计。(计算中取,,)求:
(1)从平台飞出到A点,人和车运动的水平距离;
(2)人和车运动到达圆弧轨道A点时对轨道的压力大小;
(3)人和车运动到圆弧轨道最低点速度,此时对轨道的压力大小。
4 / 8
参考答案:
一、绳模型
1.D
2.C
3.A
4.C
5.D
6. (1);(2)最低点,;(3)4.8m,10m/s,与水平面成角向下
【详解】(1)小球要做完整圆周运动,在最高点当重力提供向心力时,速度最小,则有 其中,解得
(2)当小球运动到最低点时,小球速度最大,此时根据牛顿第二定律有
可知此时绳子的张力最大,所以小球最低点时绳最易被拉断。此时有
解得,绳恰被拉断时小球的角速度大小为
(3)绳断后小球做平抛运动,平抛运动的初速度为
根据平抛规律,竖直方向上有
解得,绳断后小球落到地面的时间为
则小球落地点距转轴的水平距离为
小球落到地面时,竖直方向的分速度大小为
则落地速度的大小为
而小球速度偏转角的正切值为 则小球落地速度的方向为与水平面成角向下。
7. (1)10m/s;(2)10m;(3),
【详解】(1)设绳断时小球的线速度大小为v,根据牛顿第二定律有
解得
(2)绳断后小球做平抛运动,根据平抛运动规律有
解得
(3)落地时的竖直速度
落地速度与水平地面的夹角 落地速度
二、管道模型
8.B
9.B
10.D
11.D
12.A
13. (1)10m/s,;(2)55N;(3)107.2N
【详解】(1)经过C点恰好沿切线进入圆弧轨道,对于A到C的平抛运动过程
根据 解得
(2)根据 在A点 解得
(3)在C点 解得
根据牛顿第三定律可知
14. (1)1.2m;(2)5580N;(3)7740N
【详解】(1)在A点,根据平抛运动推论 得
(2)人和车在A点的竖直分速度为
A点的速度为
根据牛顿第二定律 得
根据牛顿第三定律,人和车运动到达圆弧轨道A点时对轨道的压力大小为5580N。
(3)在最低点,根据牛顿第二定律 得
根据牛顿第三定律,人和车运动到达最低点时对轨道的压力大小为7740N。
答案第2页,共2页
答案第1页,共2页
(绳模型、管道模型)
一、绳模型
1.飞飞老师心灵手巧,用生活中常见的细绳和塑料容器制作“水流星”模型。如图所示,球形容器中盛有质量为m的清水,然后使其在竖直平面内做半径为L的圆周运动(不考虑细绳和容器质量,重力加速度为g)。则下列说法正确的是( )
A.“水流星”通过最高点时,绳子张力不可以为零
B.“水流星”通过最高点时,清水恰好不流出来的速度是0
C.假如“水流星”可在竖直面内做匀速圆周运动,则“水流星”通过最低点和最高点,细绳的张力差为
D.假如“水流星”可在竖直面内做匀速圆周运动,则“水流星”通过最低点和最高点,细绳的张力差为
2.如图所示,细绳的一端固定于O点,另一端系一个小球,在O点的正下方钉一个钉子P,小球从左侧一定高度摆下(整个过程无能量损失)。已知小球经过最低点时,速度大小不变,则下列说法中正确的是( )
A.在摆动过程中,小球所受重力和绳子拉力的合力始终等于向心力
B.小球经过最低点时,加速度不变
C.钉子位置离O点越远,绳就越容易断
D.钉子位置离O点越近,绳就越容易断
3.如图所示,一根不可伸长的轻绳一端固定在O点,另一端拴一小球在竖直面内做圆周运动,a、b、c、d为其运动轨迹上的四个点,其中a为最高点,d为最低点,b、c两点的连线为圆周的水平直径,不计空气阻力,则在小球做圆周运动的过程中,轻绳对小球的拉力可能为零的位置是( )
A.a点 B.b点 C.c点 D.d点
4.如图甲,一长为R且不可伸长的轻绳一端固定在点O,另一端系住一小球,使小球在竖直面内做圆周运动.若小球经过最高点时速度大小为、绳子拉力大小为,则与的关系如图乙所示,下列说法中正确的是( )
A.绳长不变,用质量更小的球做实验,得到的图线斜率更大
B.小球质量不变,换绳长更长的轻绳做实验,图线点的位置不变
C.利用该装置可以得出小球的质量
D.利用该装置可以得出重力加速度
5.一定质量的小球由轻绳a和b分别系于一轻质竖直细杆的A点和B点,如图所示.当轻杆绕轴匀速转动时,带动小球在水平面内做匀速圆周运动,转动过程中绳a、b均处于伸直状态,且b绳水平,下列说法正确的是( )
A.绳a张力可能为零 B.绳b中张力不可能为零
C.角速度越大,绳a的拉力越大 D.若剪断b绳,绳a的拉力大小可能不变
6.如图,长为的细绳一端拴一质量为的小球,另一端固定在点。现使小球在竖直平面内做完整的圆周运动,转轴离地高,绳所能承受的最大张力为。
(1)求小球通过最高点时最小速度的大小;
(2)分析小球在何位置绳最易被拉断 求出在此位置绳恰被拉断时小球的角速度大小;
(3)在(2)的情况下,求小球落地点距转轴的水平距离及落地速度的大小和方向。
7.如图所示,用长度的轻绳,拴着一质量的小球(视为质点)在竖直面内做圆周运动,已知绳子能够承受的最大张力,圆心O离水平地面的高度,小球在最低点时轻绳恰好断开,不计空气阻力,取重力加速度大小,求:
(1)绳断时小球的线速度大小;
(2)绳断后小球的落地点与绳断时小球所在位置间的水平距离。
(3)小球落地的速度大小及落地速度与水平地面的夹角。
二、管道模型
8.如图所示,过山车的轨道可视为竖直平面内半径为的圆轨道。质量为的游客随过山车一起运动,当游客以速度经过圆轨道最高点时( )
A.处于超重状态 B.加速度方向竖直向下
C.速度大小一定为 D.对座椅的作用力为
9.滚筒洗衣机静止于水平地面上,已脱净水的衣物随滚筒一起在竖直平面内做匀速圆周运动,滚筒截面如图所示。若质量为m的衣物在最高点A对滚筒恰好无作用力,重力加速度大小为g,则衣物在最低点B对滚筒的压力大小为( )
A.mg B.2mg C.3mg D.4mg
10.如图所示,光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知小球在最低点时对轨道的压力大小为N1,速度大小为v1,在最高点时对轨道的压力大小为N2,速度大小为v2,重力加速度大小为g,且v1、v2满足关系式,则N1-N2的值为( )
A.3mg B.4mg C.5mg D.6mg
11.如图质量为m的小球在竖直平面内的光滑圆轨道内做圆周运动。圆轨道半径为R。小球经过最高点时刚好不脱离圆轨道。则其通过最高点时,以下说法正确的是( )
A.小球对圆环的压力大小等于mg B.小球受到的向心力与重力等大反向
C.小球的线速度大小等于 D.小球的向心加速度大小等于g
12.甲图是质量为m的小球,在竖直平面内绕O点做半径为R的圆周运动(OA为细绳);乙图是质量为m的小球,在竖直平面内绕O点做半径为R的圆周运动(OB为轻质杆);丙图是质量为m的小球,在半径为R的竖直光滑圆轨道内侧做圆周运动;丁图是质量为m的小球在竖直放置的半径为R的光滑圆形管道内做圆周运动。则下列说法正确的是( )
A.甲丙图中,小球通过最高点的最小速度都是
B.乙丁图中,小球通过最高点的最小速度都是
C.在丁图中,小球在水平线ab以下管道中运动时,外侧管壁对小球一定无作用力
D.在丁图中,小球在水平线ab以上管道中运动时,内侧管壁对小球一定有作用力
13.如图所示,AB为竖直光滑圆弧的直径,其半径R=0.9m,A端沿水平方向。水平轨道BC与半径r=0.9m的光滑圆弧轨道CD相接于C点,D为圆轨道的最低点,圆弧轨道CD、DE对应的圆心角θ=37°。一质量为M=0.9kg的物块(视为质点)从水平轨道上某点以某一速度冲上竖直圆轨道,并从A点飞出,经过C点恰好沿切线进入圆弧轨道,取g=10m/s ,sin37°=0.6,cos37°=0.8。求:
(1)物块到达C点时的速度大小;
(2)在A点受到的弹力大小FA;
(3)物体对C点的压力大小FC;
14.如图所示,摩托车做腾跃特技表演,沿曲面冲上高顶部水平高台,接着以水平速度离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑。A、B为圆弧两端点,其连线水平。已知圆弧半径为,圆弧所对应圆心角,人和车的总质量为,特技表演的全过程中,空气阻力忽略不计。(计算中取,,)求:
(1)从平台飞出到A点,人和车运动的水平距离;
(2)人和车运动到达圆弧轨道A点时对轨道的压力大小;
(3)人和车运动到圆弧轨道最低点速度,此时对轨道的压力大小。
4 / 8
参考答案:
一、绳模型
1.D
2.C
3.A
4.C
5.D
6. (1);(2)最低点,;(3)4.8m,10m/s,与水平面成角向下
【详解】(1)小球要做完整圆周运动,在最高点当重力提供向心力时,速度最小,则有 其中,解得
(2)当小球运动到最低点时,小球速度最大,此时根据牛顿第二定律有
可知此时绳子的张力最大,所以小球最低点时绳最易被拉断。此时有
解得,绳恰被拉断时小球的角速度大小为
(3)绳断后小球做平抛运动,平抛运动的初速度为
根据平抛规律,竖直方向上有
解得,绳断后小球落到地面的时间为
则小球落地点距转轴的水平距离为
小球落到地面时,竖直方向的分速度大小为
则落地速度的大小为
而小球速度偏转角的正切值为 则小球落地速度的方向为与水平面成角向下。
7. (1)10m/s;(2)10m;(3),
【详解】(1)设绳断时小球的线速度大小为v,根据牛顿第二定律有
解得
(2)绳断后小球做平抛运动,根据平抛运动规律有
解得
(3)落地时的竖直速度
落地速度与水平地面的夹角 落地速度
二、管道模型
8.B
9.B
10.D
11.D
12.A
13. (1)10m/s,;(2)55N;(3)107.2N
【详解】(1)经过C点恰好沿切线进入圆弧轨道,对于A到C的平抛运动过程
根据 解得
(2)根据 在A点 解得
(3)在C点 解得
根据牛顿第三定律可知
14. (1)1.2m;(2)5580N;(3)7740N
【详解】(1)在A点,根据平抛运动推论 得
(2)人和车在A点的竖直分速度为
A点的速度为
根据牛顿第二定律 得
根据牛顿第三定律,人和车运动到达圆弧轨道A点时对轨道的压力大小为5580N。
(3)在最低点,根据牛顿第二定律 得
根据牛顿第三定律,人和车运动到达最低点时对轨道的压力大小为7740N。
答案第2页,共2页
答案第1页,共2页
