鲁教版九年级数学下册第5章圆5.3垂径定理测试题(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第5章圆5.3垂径定理测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-09 00:00:00 | ||
图片预览

文档简介
九年级下册第5章圆5.1垂径定理测试题(含答案)
一.选择题(共8小题)
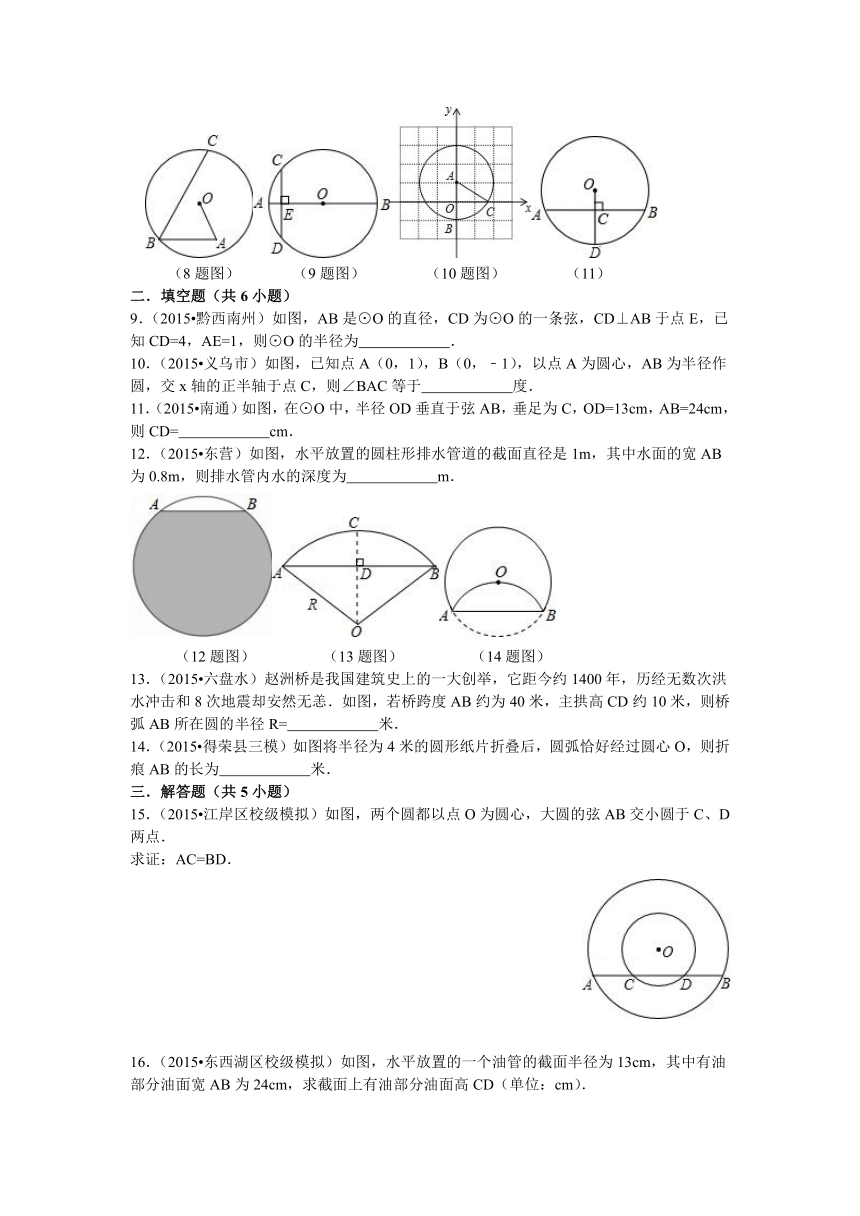
1.(2015 广元)如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B. AE=OE C. = D. △OCE≌△ODE
(1题图) (2题图) (3题图) (4题图)
2.(2015 遂宁)如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B. 4cm C. 5cm D. 6cm
3.(2015 玉林)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B. ∠C=∠BOD C. ∠C=∠B D. ∠A=∠BOD
4.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm B. 9cm C. cm D. 10cm
5.(2014秋 乐清市校级月考)一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
A.8 B. 6 C. 5 D. 4
(5题图) (6题图) (7题图)
6.(2014 温州一模)温州是著名水乡,河流遍布整个城市.某河流上建有一座美丽的石拱桥(如图).已知桥拱半径OC为5m,水面宽AB为m,则石拱桥的桥顶到水面的距离CD为( )
A.4m B. 7m C. 5+m D. 6 m
7.(2015 宜州市二模)如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为( )
A.3 B. C. 4 D.
8.(2015 武汉模拟)如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B. 6cm C. 7cm D. 8cm
(8题图) (9题图) (10题图) (11)
二.填空题(共6小题)
9.(2015 黔西南州)如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
10.(2015 义乌市)如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于 度.
11.(2015 南通)如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD= cm.
12.(2015 东营)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.
(12题图) (13题图) (14题图)
13.(2015 六盘水)赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
14.(2015 得荣县三模)如图将半径为4米的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 米.
三.解答题(共5小题)
15.(2015 江岸区校级模拟)如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
16.(2015 东西湖区校级模拟)如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求截面上有油部分油面高CD(单位:cm).
17.(2014 佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
18.(2015 永州)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
19.(2015 绵阳模拟)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
九年级下册第5章圆5.1垂径定理测试题参考答案
一.选择题(共8小题)
1.B. 2.B.3.B 4.C.5.D.6.D.7.B.8.B.
二.填空题(共6小题)
9. .10. 60 11. 8 12. 0.8 13. 25 14. 4
三.解答题(共5小题)
15.证明:作OH⊥AB于H,如图,则AH=BH,CH=DH,
∴AH﹣CH=BH﹣DH,即AC=BD.
(15题图) (16题图) (17题图) (18题图)
16.解:如图;连接OA;根据垂径定理,得AC=BC=12cm;
Rt△OAC中,OA=13cm,AC=12cm;
根据勾股定理,得:OC==5cm;∴CD=OD﹣OC=8cm;
∴油面高为8cm.
17.解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
18.(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,
∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,∴CE2=DE AE,设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
19.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,∴,∴AC=AD,
∵过圆心O的线CF⊥AD,∴AF=DF,即CF是AD的中垂线,∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,在Rt△COE中,,∴,∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,∴,
又∵BE=OE,∴OE=2,
∴,
∴.
一.选择题(共8小题)
1.(2015 广元)如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B. AE=OE C. = D. △OCE≌△ODE
(1题图) (2题图) (3题图) (4题图)
2.(2015 遂宁)如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B. 4cm C. 5cm D. 6cm
3.(2015 玉林)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B. ∠C=∠BOD C. ∠C=∠B D. ∠A=∠BOD
4.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm B. 9cm C. cm D. 10cm
5.(2014秋 乐清市校级月考)一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
A.8 B. 6 C. 5 D. 4
(5题图) (6题图) (7题图)
6.(2014 温州一模)温州是著名水乡,河流遍布整个城市.某河流上建有一座美丽的石拱桥(如图).已知桥拱半径OC为5m,水面宽AB为m,则石拱桥的桥顶到水面的距离CD为( )
A.4m B. 7m C. 5+m D. 6 m
7.(2015 宜州市二模)如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为( )
A.3 B. C. 4 D.
8.(2015 武汉模拟)如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B. 6cm C. 7cm D. 8cm
(8题图) (9题图) (10题图) (11)
二.填空题(共6小题)
9.(2015 黔西南州)如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
10.(2015 义乌市)如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于 度.
11.(2015 南通)如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD= cm.
12.(2015 东营)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.
(12题图) (13题图) (14题图)
13.(2015 六盘水)赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
14.(2015 得荣县三模)如图将半径为4米的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 米.
三.解答题(共5小题)
15.(2015 江岸区校级模拟)如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
16.(2015 东西湖区校级模拟)如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求截面上有油部分油面高CD(单位:cm).
17.(2014 佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
18.(2015 永州)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
19.(2015 绵阳模拟)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
九年级下册第5章圆5.1垂径定理测试题参考答案
一.选择题(共8小题)
1.B. 2.B.3.B 4.C.5.D.6.D.7.B.8.B.
二.填空题(共6小题)
9. .10. 60 11. 8 12. 0.8 13. 25 14. 4
三.解答题(共5小题)
15.证明:作OH⊥AB于H,如图,则AH=BH,CH=DH,
∴AH﹣CH=BH﹣DH,即AC=BD.
(15题图) (16题图) (17题图) (18题图)
16.解:如图;连接OA;根据垂径定理,得AC=BC=12cm;
Rt△OAC中,OA=13cm,AC=12cm;
根据勾股定理,得:OC==5cm;∴CD=OD﹣OC=8cm;
∴油面高为8cm.
17.解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
18.(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,
∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,∴CE2=DE AE,设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
19.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,∴,∴AC=AD,
∵过圆心O的线CF⊥AD,∴AF=DF,即CF是AD的中垂线,∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,在Rt△COE中,,∴,∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,∴,
又∵BE=OE,∴OE=2,
∴,
∴.
