2023-2024学年度华东师大版数学九年级下册28.1.1普查和抽样调查课件 (共21张PPT)
文档属性
| 名称 | 2023-2024学年度华东师大版数学九年级下册28.1.1普查和抽样调查课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 143.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
28.1.1 普查和抽样调查
九年级下
华师版
1.了解普查、抽样调查的概念,学会选择合适的调查方式.
2.理解总体、个体、样本、样本的容量的概念.
学习目标
重点
重点
先给大家讲一个小故事:
妈妈:“孩子,再帮妈妈买鸡蛋去.”
妈妈:“这次注意点,上次你买的鸡蛋有好几个是坏的.”
(时间过了一会儿……)
孩子:“妈妈,这次的鸡蛋全是好的,我每个都打开看过了.”
妈妈:“啊!”
新课引入
一 普查和抽样调查
探究
问题1 你们班里每个同学的家里各有多少人?平均每个家庭有多少人?
班级学生家庭人口数统计表
姓名 … 人口总数 平均数
家庭人口数 …
可以调查班上每一名学生,将结果填入下表,就可以计算出结果.
新知学习
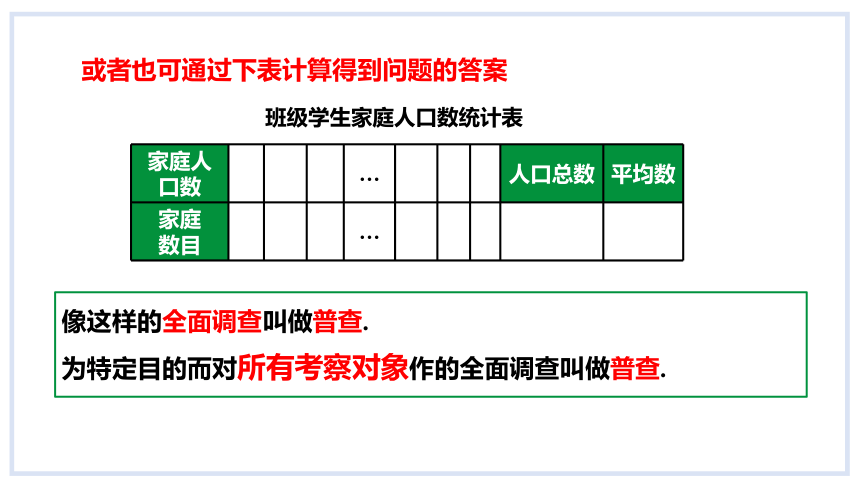
班级学生家庭人口数统计表
家庭人口数 … 人口总数 平均数
家庭 数目 …
或者也可通过下表计算得到问题的答案
像这样的全面调查叫做普查.
为特定目的而对所有考察对象作的全面调查叫做普查.
问题2 2020年,全国平均每个家庭有多少人?
第2个问题稍难一些,因为要调查的家庭数太多,不过利用2020年第七次全国人口普查数据,我们还是能够回答的.在中华人民共和国国家统计局网上,能够查到全国人口普查数据公报:“大陆31个省、自治区、直辖市共有家庭户49416万户,家庭户人口为129281万人,平均每个家庭户的人口为2.62人.”
问题3 今年,全国平均每个家庭有多少人?
第3个问题最难回答,我国一般每十年进行一次全国人口普查,每五年进行一次全国1%人口的抽样调查.
所谓全国1%人口的抽样调查是指从全国总人口中抽取1%,然后对这部分人进行的调查.
我们没有今年的现成数据,只能在2020年数据的基础上,再结合近几年来我国平均每个家庭户的人口数在下降这一事实,估计一个答案了.
为特定目的而对部分考察对象作的全面调查叫做抽样调查.
归纳
普查:为特定目的而对所有考察对象作的全面调查叫做普查.
抽样调查:为特定目的而对部分考察对象作的全面调查叫做抽样调查.
例1 下列调查中,哪些适宜抽样调查,哪些适宜普查?
(1)调查我市中学生每天做作业的时间;
(2)学校招聘教师,对应聘人员进行面试;
(3)调查某班学生对“中国梦”的知晓率;
解:(1)涉及的范围较大,适宜抽样调查.
(3)某班学生的人数有限,适宜普查.
(2)学校招聘教师,应对所有应聘人员进行面试,所以应采用普查.
(4)调查一架“歼20”隐形战机各零部件的质量;
(5)调查里约热内卢奥运会100 m 跨栏决赛参赛运动员兴奋剂的使用情况.
解:(4)考虑到一架“歼20”隐形战机各零部件的数量有限,并且其安全性对质量的要求较高,适宜普查.
(5)调查里约热内卢奥运会100 m 跨栏决赛参赛运动员兴奋剂的使用情况适宜普查.
在什么情况下使用全面调查?什么情况下使用抽样调查?
思考
选择普查的情况有:
1. 当调查的对象个数较少,调查容易进行时,可选择普查;
2. 当调查的结果有特别要求,或调查的结果有特殊意义时,如国家的人口普查,可选择普查.
选择抽样调查的情况有:
1. 当被调查的对象数目较多时,普查的工作量较大,可选择抽样调查;
2. 当客观条件限制,无法对所有调查对象进行全面调查时,可选择抽样调查;
3. 当调查具有破坏性时,可选择抽样调查.
普查与抽样调查的比较
普查 抽样调查
优点
缺点
通过调查总体来收集数据,调查的结果准确.
通过调查样本来收集数据,工作量较小,便于进行.
工作量大,难度大,而且有些调查不宜使用普查
调查结果往往不如普查得到的结果准确.
1.下列调查中,你认为应该采用哪种调查方式,并说出理由.
①调查池塘里鱼的数量;
②调查你们学校七年级学生的体重;
③调查一批彩电的质量情况;
④调查你们班学生早餐是否有喝牛奶的习惯;
⑤2017年沙门氏菌在美国扩散,其中有关数据的收集所作的调查.
抽样调查
抽样调查
抽样调查
普查
普查
针对训练
二 总体、个体、样本与样本容量
在统计里,为了叙述上的方便,我们引入了几个概念:
总体:所要考察的对象的全体叫做总体;
个体:组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包含的个体的数量叫做样本容量.
注意:样本容量没有单位.
例2 分别指出下列调查中的总体、个体、样本和样本容量.
(1)为调查电风扇的使用寿命,从一批电风扇中抽取20台进行测试;
解:(1)电风扇的使用寿命为总体,每一个电风扇使用寿命为个体,抽出来20台的使用寿命为样本,样本容量为20.
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
解:(2)该校七年级学生每周用于做课外作业的时间为总体,该校每名七年级学生做课外作业的时间为个体,从七年级中抽出来调查的50名学生每周用于做课外作业的时间为样本,样本容量为50.
1.某市有3万名学生参加2019年的中考,想要了解这3万名考生的中考成绩,从中抽取了500名考生的中考成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本
B.每个考生的中考成绩是个体
C.3万名考生是总体
D.500名考生是样本容量
B
针对训练
1.为了解全校学生的上学方式,需要在全校1200名学生中抽取300名学生进行调查.
(1)下列抽取学生的方法合理的是( )
A. 在七年级学生中随机抽取300 名
B. 在男生中随机抽取300名
C. 在全校随机抽取300名师生
D. 在全校随机抽取300名学生
D
随堂练习
(2)此调查方式为__________;
(3)此次调查的总体为___________________________________,个体为___________________________,样本为______________________,样本容量为________.
抽样调查
全校1200名学生的上学方式
每一名学生的上学方式
300名学生的上学方式
300
数量较少;不具有破坏性;研究问题要求情况真实,准确
数量较多;受客观条件限制;具有破坏性
总体
个体
样本
样本容量
普查和
抽样调查
普查
抽样调查
课堂小结
28.1.1 普查和抽样调查
九年级下
华师版
1.了解普查、抽样调查的概念,学会选择合适的调查方式.
2.理解总体、个体、样本、样本的容量的概念.
学习目标
重点
重点
先给大家讲一个小故事:
妈妈:“孩子,再帮妈妈买鸡蛋去.”
妈妈:“这次注意点,上次你买的鸡蛋有好几个是坏的.”
(时间过了一会儿……)
孩子:“妈妈,这次的鸡蛋全是好的,我每个都打开看过了.”
妈妈:“啊!”
新课引入
一 普查和抽样调查
探究
问题1 你们班里每个同学的家里各有多少人?平均每个家庭有多少人?
班级学生家庭人口数统计表
姓名 … 人口总数 平均数
家庭人口数 …
可以调查班上每一名学生,将结果填入下表,就可以计算出结果.
新知学习
班级学生家庭人口数统计表
家庭人口数 … 人口总数 平均数
家庭 数目 …
或者也可通过下表计算得到问题的答案
像这样的全面调查叫做普查.
为特定目的而对所有考察对象作的全面调查叫做普查.
问题2 2020年,全国平均每个家庭有多少人?
第2个问题稍难一些,因为要调查的家庭数太多,不过利用2020年第七次全国人口普查数据,我们还是能够回答的.在中华人民共和国国家统计局网上,能够查到全国人口普查数据公报:“大陆31个省、自治区、直辖市共有家庭户49416万户,家庭户人口为129281万人,平均每个家庭户的人口为2.62人.”
问题3 今年,全国平均每个家庭有多少人?
第3个问题最难回答,我国一般每十年进行一次全国人口普查,每五年进行一次全国1%人口的抽样调查.
所谓全国1%人口的抽样调查是指从全国总人口中抽取1%,然后对这部分人进行的调查.
我们没有今年的现成数据,只能在2020年数据的基础上,再结合近几年来我国平均每个家庭户的人口数在下降这一事实,估计一个答案了.
为特定目的而对部分考察对象作的全面调查叫做抽样调查.
归纳
普查:为特定目的而对所有考察对象作的全面调查叫做普查.
抽样调查:为特定目的而对部分考察对象作的全面调查叫做抽样调查.
例1 下列调查中,哪些适宜抽样调查,哪些适宜普查?
(1)调查我市中学生每天做作业的时间;
(2)学校招聘教师,对应聘人员进行面试;
(3)调查某班学生对“中国梦”的知晓率;
解:(1)涉及的范围较大,适宜抽样调查.
(3)某班学生的人数有限,适宜普查.
(2)学校招聘教师,应对所有应聘人员进行面试,所以应采用普查.
(4)调查一架“歼20”隐形战机各零部件的质量;
(5)调查里约热内卢奥运会100 m 跨栏决赛参赛运动员兴奋剂的使用情况.
解:(4)考虑到一架“歼20”隐形战机各零部件的数量有限,并且其安全性对质量的要求较高,适宜普查.
(5)调查里约热内卢奥运会100 m 跨栏决赛参赛运动员兴奋剂的使用情况适宜普查.
在什么情况下使用全面调查?什么情况下使用抽样调查?
思考
选择普查的情况有:
1. 当调查的对象个数较少,调查容易进行时,可选择普查;
2. 当调查的结果有特别要求,或调查的结果有特殊意义时,如国家的人口普查,可选择普查.
选择抽样调查的情况有:
1. 当被调查的对象数目较多时,普查的工作量较大,可选择抽样调查;
2. 当客观条件限制,无法对所有调查对象进行全面调查时,可选择抽样调查;
3. 当调查具有破坏性时,可选择抽样调查.
普查与抽样调查的比较
普查 抽样调查
优点
缺点
通过调查总体来收集数据,调查的结果准确.
通过调查样本来收集数据,工作量较小,便于进行.
工作量大,难度大,而且有些调查不宜使用普查
调查结果往往不如普查得到的结果准确.
1.下列调查中,你认为应该采用哪种调查方式,并说出理由.
①调查池塘里鱼的数量;
②调查你们学校七年级学生的体重;
③调查一批彩电的质量情况;
④调查你们班学生早餐是否有喝牛奶的习惯;
⑤2017年沙门氏菌在美国扩散,其中有关数据的收集所作的调查.
抽样调查
抽样调查
抽样调查
普查
普查
针对训练
二 总体、个体、样本与样本容量
在统计里,为了叙述上的方便,我们引入了几个概念:
总体:所要考察的对象的全体叫做总体;
个体:组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包含的个体的数量叫做样本容量.
注意:样本容量没有单位.
例2 分别指出下列调查中的总体、个体、样本和样本容量.
(1)为调查电风扇的使用寿命,从一批电风扇中抽取20台进行测试;
解:(1)电风扇的使用寿命为总体,每一个电风扇使用寿命为个体,抽出来20台的使用寿命为样本,样本容量为20.
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
解:(2)该校七年级学生每周用于做课外作业的时间为总体,该校每名七年级学生做课外作业的时间为个体,从七年级中抽出来调查的50名学生每周用于做课外作业的时间为样本,样本容量为50.
1.某市有3万名学生参加2019年的中考,想要了解这3万名考生的中考成绩,从中抽取了500名考生的中考成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本
B.每个考生的中考成绩是个体
C.3万名考生是总体
D.500名考生是样本容量
B
针对训练
1.为了解全校学生的上学方式,需要在全校1200名学生中抽取300名学生进行调查.
(1)下列抽取学生的方法合理的是( )
A. 在七年级学生中随机抽取300 名
B. 在男生中随机抽取300名
C. 在全校随机抽取300名师生
D. 在全校随机抽取300名学生
D
随堂练习
(2)此调查方式为__________;
(3)此次调查的总体为___________________________________,个体为___________________________,样本为______________________,样本容量为________.
抽样调查
全校1200名学生的上学方式
每一名学生的上学方式
300名学生的上学方式
300
数量较少;不具有破坏性;研究问题要求情况真实,准确
数量较多;受客观条件限制;具有破坏性
总体
个体
样本
样本容量
普查和
抽样调查
普查
抽样调查
课堂小结
