2023-2024学年苏科版数学八年级下册 7.2统计图的选用 讲义(表格式)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级下册 7.2统计图的选用 讲义(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 705.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 09:53:29 | ||
图片预览




文档简介
7.2统计图的选用(讲义)
教学目的: 掌握条形统计图、扇形统计图、折线统计图的特点 三种统计图的区分 从统计图中获取信息
教学重难点: 统计图的画法 通过统计图获取所需信息
知识梳理
【知识点一】条形统计图、扇形统计图、折线统计图的特点 统计图能直观形象地反映出事情的发展、变化或总体与部分的关系,统计中常见的统计图有条形图、扇形图、折线图,它们各有各的特点,可以从不同的角度清楚、有效地描述数据. 1.条形统计图 (1)特点 ①用条形统计图中每个小长方形的高地表示数量的多少. ②条形统计图能清楚地表示出每个部分的具体数量. (2)缺点 ①对于条形统计图,人们习惯于条形柱的高度看相应的数量,若条形柱的高度与相应的数量不成正比,就容易给人造成错觉. ②条形统计图不能表示各部分在总体中所占的百分比 2.扇形统计图 (1)特点 ①用圆代表总体,用圆内的每一个扇形代表总体的一部分. ②扇形统计图能清楚地表示出各部分在总体中所占的百分比. (2)缺点 ①在两个扇形统计图中,若一个统计图中的某一部分A所占的百分比比另一个统计图中的某一部分B所占的百分比多,这样容易造成A的数量大于B的数量的错觉. ②扇形统计图不能清楚地表明每一部分的具体数量. (3)制作扇形统计图的一般步骤 ①算出个部分数量占总体数量的百分比; ②算出表示各部分的扇形的圆心角度数(圆心角度数=360°X百分比); ③取适当的半径画一个圆,再按上面算出的圆心角度数在圆里画出各个扇形; ④分别在每个扇形中标明对应部分的名称和所占的百分比(最好用不同的颜色或条纹把各个扇形区分开来). 3.折线统计图 (1)特点 ①每个点代表数据的大小,用折线的起伏表示数量的增减变化. ②折线统计图能清楚的反映数据的变化趋势. (2)缺点 ①对于折线统计图,若横坐标被“压缩”,纵坐标被“放大”,就会显得数量的变化速度加快;若纵坐标被“放大”,纵坐标被“压缩”,就会显得数量的变化速度减慢. ②折线统计图不能表示各部分在总体中所占的百分比.
典型例题
【例1】“双减”政策实施后,某校为了解八年级学生每天的作业完成时间的变化情况,最适合采用下列哪种统计图来进行描述( ) A.条形统计图 B.扇形统计图 C.折线统计图 D.以上三种统计图都可以 【例2】某次数学测验,抽取部分同学的成绩(得分为整数),整理制成统计表如下,根据表中信息,下列描述不正确 的是 分数段人数41018126
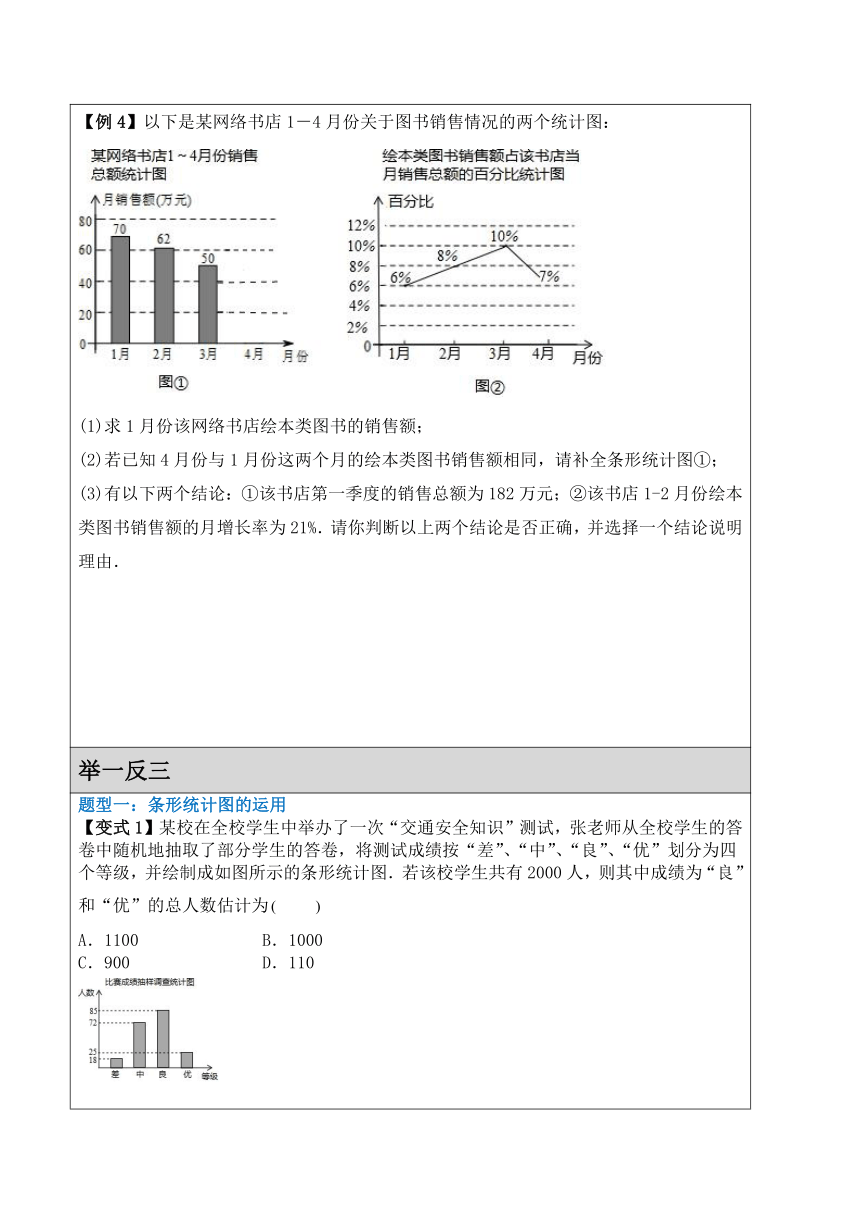
A.抽样的学生共有50人 B.估计这次测试的及格率在左右 C.估计优秀率分以上)在左右 D.这一分数段的频率为10 【例3】高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图: 小亮根据这两幅不完整的统计图得出以下五个结论:①样本容量为400 ;②类型B的人数为120人;③类型C所占百分比为;④类型C所对应的扇形的圆心角为126°; ⑤类型D的人数是类型B的人数的.你判断一下小亮结论中错误的是_______ . (请填写序号) 【例4】以下是某网络书店1-4月份关于图书销售情况的两个统计图: (1)求1月份该网络书店绘本类图书的销售额; (2)若已知4月份与1月份这两个月的绘本类图书销售额相同,请补全条形统计图①; (3)有以下两个结论:①该书店第一季度的销售总额为182万元;②该书店1-2月份绘本类图书销售额的月增长率为21%.请你判断以上两个结论是否正确,并选择一个结论说明理由.
举一反三
题型一:条形统计图的运用 【变式1】某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为 A.1100 B.1000 C.900 D.110 【变式2】如图所示是某单位考核情况条形统计图(、、三个等级),则下面的回答正确的是( ) A.等级人最少,占总数的 B.该单位共有120人 C.等级人比等级人多 D.等级人最多,占总人数的 【变式3】某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下: 人数每人所作标本数
根据表中提供的信息,回答下列问题: (1)该组共有学生多少人? (2)制作标本数在个及以上的人数在全组人数中所占比例? (3)平均每人制作多少个标本? (4)补全条形统计图. 题型二:扇形统计图的运用 【变式1】某校学生到校方式情况统计图,若该校步行到校的学生有100人,则乘公共汽车到校的学生有 A.200 B.70 C.180 D.125 【变式2】某学校将为初一学生开设A、B、C、D、E、F共6门选修课,选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如下尚不完整的统计图表: 选修课ABCDEF人数4060100
根据图表提供的信息,下列结论错误的是( ) A.这次被调查的学生人数为400人 B.被调查的学生中喜欢选修课E、F的人数分别为80、70 C.喜欢选修课C的人数最少 D.扇形统计图中E部分扇形的圆心角为 【变式3】 现在同学们的课余时间更多了,大家是怎么安排自己的课余时间的呢?如图所示是六(1)班同学课余时间统计图. (1)选择户外运动的同学占全班人数的____%. (2)选择_____的占全班人数最多. (3)已知户外运动人数比阅读人数多5人,六(1)班一共有多少名学生? 题型三:折线统计图的运用 【变式1】如图,折线图描述的是某地某日的气温变化情况,由图可知气温为的整点时刻有 A.1个 B.2个 C.3个 D.4个 【变式2】如图是某地2月18日到23日浓度和空气质量的统计图(当不大于100时称空气质量为“优良”).由图可得下列说法:①18日的浓度最低;②21日的浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数与浓度有关.其中正确的是________(填序号即可) 【变式3】文具店售卖与和两种规格的笔记本,规格每本利润为元,规格每本利润为元,文具店将两种规格的销量分别用折线图表示,同时将用表格表示前5个月的总销量与利润;根据上述信息,解答下列问题: 月份1月2月3月4月5月总销量909298105a总利润111b
笔记本销量图 (1)填空:______、______; (2)从1月到5月,规格笔记本的销量呈______趋势,规格笔记本的销量呈______趋势(用“上升”或“下降”填空); (3)文具店预计9月份这两种规格的笔记本销量需求很大,估计可达400本,相应利润将达390元,根据估计,请你计算文具店9月份两种规格笔记本的销量各是多少. 题型四:条形、扇形、折线统计图的综合运用 【变式1】某电子产品店今年1~4月的电子产品销售总额如图①,其中一款平板电脑的销售额占当月电子产品销售总额的百分比如图②.根据图中信息,以下四个推断合理的是__________.(填序号) ①从1月到4月,电子产品销售总额为290万元; ②平板电脑2~4月的销售额占当月电子产品销售总额的百分比与1月份相比都下降了; ③平板电脑4月份的销售额比3月份有所下降; ④今年1~4月中,平板电脑售额最低的是3月. 【变式2】为了了解2022年某地区5万名大、中、小学生3分钟跳绳成绩情况,教育部门从这三类学生群体中各抽取了的学生进行检测.整理样本数据,并结合2018年抽样结果,得到下列统计图. (1)本次检测抽取了大、中、小学生共______名,其中小学生______名; (2)根据抽样的结果,估计2022年该地区5万名大、中、小学生,3分钟跳绳成绩合格的中学生人数为______名; (3)比较2018年与2022年抽样学生3分钟跳绳成绩合格率情况,写出一条正确的结论. 【变式3】为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的时间,设被调查的每名学生每周课外阅读的总时间为x小时,将它分为4个等级:A(),B(),C(),D(),并根据调查结果绘制了如图两幅不完整的统计图: 请你根据统计图的信息,解决下列问题: (1)本次共调查了______名学生; (2)在扇形统计图中,若A等级所占比例为m%,则m的值为_____,等级D所对应的扇形的圆心角为________°; (3)请计算C的学生数目并补全条形统计图; (4)全校1200名学生,估计阅读时间不少于6小时的学生有多少名?
小试牛刀
一、选择题(共5题) 1.记录一个病人体温的变化情况,选用的统计图最好是( ) A.扇形统计图 B.条形统计图 C.折线统计图 D.都可以 2.在条形统计图上________,才会减少直观上的错觉.( ) A.横轴与纵轴都必须从0开始 B.横轴与纵轴都不必从0开始 C.纵轴不必从0开始,横轴必须从0开始 D.横轴不必从0开始,纵轴必须从0开始 3.为迎接党的二十大胜利召开,某校开展了“学党史,悟初心”系列活动.学校对学生参加各项活动的人数进行了调查,并将数据绘制成如下统计图.若参加“书法”的人数为80人,则参加“大合唱”的人数为( ) A.60人 B.100人 C.160人 D.400人 4.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如表所示,则下列说法正确的是( ) 年级七年级八年级九年级合格人数270262254
A.七年级的合格率最高 B.八年级的学生人数为262名 C.八年级的合格率高于全校的合格率 D.九年级的合格人数最少 5.某地区经过三年的乡村振兴建设,农村的经济收入是振兴前的2倍.为更好地了解该地区农村的经济收入变化情况,统计了该地区乡村振兴建设前后农村的经济收入构成比例,绘制了下面的扇形统计图,则下列说法错误的是( ) A.乡村振兴建设后,养殖收入是振兴前的2倍 B.乡村振兴建设后,种植收入减少 C.乡村振兴建设后,其它收入是振兴前的2.5倍 D.乡村振兴建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 二、填空题(共5题) 6.在一个扇形统计图中,表示种植苹果树面积的扇形圆心角为,那么苹果树面积占总种植面积的百分比为 . 7.想了解本周气温的变化情况,最适合采用 统计图.(填“扇形”或“折线”) 8.某中学共40位同学参加了演讲比赛,分段统计参赛同学的成绩,结果如下(分数为整数,满分为100分) 分数段(分〕61~7071~8081~9091~100人数51016
则_________;若制作成扇形统计图,那么81~90分数段所对应扇形的圆心角____°. 9.某校开展“我最喜爱的一项体育运动”调查,每名学生必选且只能选一项.现随机抽查了若干名学生,并将其结果绘制成不完整的条形图和扇形图.在抽查的学生中,喜欢足球运动的人数为______. 10.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初二学生进行了问卷调查,其中一项是疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图不完整,由图中信息可知,下列结论正确的序号 . 本次调查的样本容量是; 选“责任”的有人; 扇形统计图中“生命”所对应的扇形圆心角的大小为; 选“感恩”的人数最多. 三、解答题(共5题) 11.某校开展阳光体育运动,调查了八年级学生喜欢的球类活动(每人只选一项自己最喜欢的球类项目),并将调查情况制成如下统计表和统计图(不完整).请将统计表和统计图补充完整. 球类项目乒乓球篮球足球排球人数30人______人______人______人
12.有人针对公交车上是否主动让座做了一次调查,结果如下: (1)参与本次调查的人数是多少? (2)“从来不让座的人”占调查总人数的百分比是多少? (3)面对以上的调查结果,你还能得到什么结论? 13.由于气温骤变,小米突然感冒了.下面是她的体温记录折线图.回答下列问题: (1)小米的体温最高是 ℃,最低是 ℃. (2)她的体温在哪段时间里下降得最快?在哪段时间里比较稳定?分析其原因. (3)图中的横虚线表示什么? 14.某音像制品店某一天的销售的情况如图: (1)从条形统计图看,民歌类唱片与流行歌曲唱片销售量之比大约是多少?从扇形统计图看呢? (2)要使读者清楚地看出各类音像制品的销售量之比,条形统计图应做怎样的改动? 15.某校举办球赛,分为若干组,其中第一组有A,B,C,D,E五个队.这五个队要进行单循环赛,即每两个队之间要进行一场比赛,每场比赛采用三局两胜制,即三局中胜两局就获胜.每场比赛胜负双方根据比分会获得相应的积分,积分均为正整数.这五个队完成所有比赛后得到如下的积分表. 根据上表回答下列问题: (1)第一组一共进行了 场比赛,A队的获胜场数x为 ; (2)当B队的总积分y=6时,上表中m处应填 ,n处应填 ; (3)写出C队总积分p的所有可能值为: .
教学目的: 掌握条形统计图、扇形统计图、折线统计图的特点 三种统计图的区分 从统计图中获取信息
教学重难点: 统计图的画法 通过统计图获取所需信息
知识梳理
【知识点一】条形统计图、扇形统计图、折线统计图的特点 统计图能直观形象地反映出事情的发展、变化或总体与部分的关系,统计中常见的统计图有条形图、扇形图、折线图,它们各有各的特点,可以从不同的角度清楚、有效地描述数据. 1.条形统计图 (1)特点 ①用条形统计图中每个小长方形的高地表示数量的多少. ②条形统计图能清楚地表示出每个部分的具体数量. (2)缺点 ①对于条形统计图,人们习惯于条形柱的高度看相应的数量,若条形柱的高度与相应的数量不成正比,就容易给人造成错觉. ②条形统计图不能表示各部分在总体中所占的百分比 2.扇形统计图 (1)特点 ①用圆代表总体,用圆内的每一个扇形代表总体的一部分. ②扇形统计图能清楚地表示出各部分在总体中所占的百分比. (2)缺点 ①在两个扇形统计图中,若一个统计图中的某一部分A所占的百分比比另一个统计图中的某一部分B所占的百分比多,这样容易造成A的数量大于B的数量的错觉. ②扇形统计图不能清楚地表明每一部分的具体数量. (3)制作扇形统计图的一般步骤 ①算出个部分数量占总体数量的百分比; ②算出表示各部分的扇形的圆心角度数(圆心角度数=360°X百分比); ③取适当的半径画一个圆,再按上面算出的圆心角度数在圆里画出各个扇形; ④分别在每个扇形中标明对应部分的名称和所占的百分比(最好用不同的颜色或条纹把各个扇形区分开来). 3.折线统计图 (1)特点 ①每个点代表数据的大小,用折线的起伏表示数量的增减变化. ②折线统计图能清楚的反映数据的变化趋势. (2)缺点 ①对于折线统计图,若横坐标被“压缩”,纵坐标被“放大”,就会显得数量的变化速度加快;若纵坐标被“放大”,纵坐标被“压缩”,就会显得数量的变化速度减慢. ②折线统计图不能表示各部分在总体中所占的百分比.
典型例题
【例1】“双减”政策实施后,某校为了解八年级学生每天的作业完成时间的变化情况,最适合采用下列哪种统计图来进行描述( ) A.条形统计图 B.扇形统计图 C.折线统计图 D.以上三种统计图都可以 【例2】某次数学测验,抽取部分同学的成绩(得分为整数),整理制成统计表如下,根据表中信息,下列描述不正确 的是 分数段人数41018126
A.抽样的学生共有50人 B.估计这次测试的及格率在左右 C.估计优秀率分以上)在左右 D.这一分数段的频率为10 【例3】高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图: 小亮根据这两幅不完整的统计图得出以下五个结论:①样本容量为400 ;②类型B的人数为120人;③类型C所占百分比为;④类型C所对应的扇形的圆心角为126°; ⑤类型D的人数是类型B的人数的.你判断一下小亮结论中错误的是_______ . (请填写序号) 【例4】以下是某网络书店1-4月份关于图书销售情况的两个统计图: (1)求1月份该网络书店绘本类图书的销售额; (2)若已知4月份与1月份这两个月的绘本类图书销售额相同,请补全条形统计图①; (3)有以下两个结论:①该书店第一季度的销售总额为182万元;②该书店1-2月份绘本类图书销售额的月增长率为21%.请你判断以上两个结论是否正确,并选择一个结论说明理由.
举一反三
题型一:条形统计图的运用 【变式1】某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为 A.1100 B.1000 C.900 D.110 【变式2】如图所示是某单位考核情况条形统计图(、、三个等级),则下面的回答正确的是( ) A.等级人最少,占总数的 B.该单位共有120人 C.等级人比等级人多 D.等级人最多,占总人数的 【变式3】某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下: 人数每人所作标本数
根据表中提供的信息,回答下列问题: (1)该组共有学生多少人? (2)制作标本数在个及以上的人数在全组人数中所占比例? (3)平均每人制作多少个标本? (4)补全条形统计图. 题型二:扇形统计图的运用 【变式1】某校学生到校方式情况统计图,若该校步行到校的学生有100人,则乘公共汽车到校的学生有 A.200 B.70 C.180 D.125 【变式2】某学校将为初一学生开设A、B、C、D、E、F共6门选修课,选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如下尚不完整的统计图表: 选修课ABCDEF人数4060100
根据图表提供的信息,下列结论错误的是( ) A.这次被调查的学生人数为400人 B.被调查的学生中喜欢选修课E、F的人数分别为80、70 C.喜欢选修课C的人数最少 D.扇形统计图中E部分扇形的圆心角为 【变式3】 现在同学们的课余时间更多了,大家是怎么安排自己的课余时间的呢?如图所示是六(1)班同学课余时间统计图. (1)选择户外运动的同学占全班人数的____%. (2)选择_____的占全班人数最多. (3)已知户外运动人数比阅读人数多5人,六(1)班一共有多少名学生? 题型三:折线统计图的运用 【变式1】如图,折线图描述的是某地某日的气温变化情况,由图可知气温为的整点时刻有 A.1个 B.2个 C.3个 D.4个 【变式2】如图是某地2月18日到23日浓度和空气质量的统计图(当不大于100时称空气质量为“优良”).由图可得下列说法:①18日的浓度最低;②21日的浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数与浓度有关.其中正确的是________(填序号即可) 【变式3】文具店售卖与和两种规格的笔记本,规格每本利润为元,规格每本利润为元,文具店将两种规格的销量分别用折线图表示,同时将用表格表示前5个月的总销量与利润;根据上述信息,解答下列问题: 月份1月2月3月4月5月总销量909298105a总利润111b
笔记本销量图 (1)填空:______、______; (2)从1月到5月,规格笔记本的销量呈______趋势,规格笔记本的销量呈______趋势(用“上升”或“下降”填空); (3)文具店预计9月份这两种规格的笔记本销量需求很大,估计可达400本,相应利润将达390元,根据估计,请你计算文具店9月份两种规格笔记本的销量各是多少. 题型四:条形、扇形、折线统计图的综合运用 【变式1】某电子产品店今年1~4月的电子产品销售总额如图①,其中一款平板电脑的销售额占当月电子产品销售总额的百分比如图②.根据图中信息,以下四个推断合理的是__________.(填序号) ①从1月到4月,电子产品销售总额为290万元; ②平板电脑2~4月的销售额占当月电子产品销售总额的百分比与1月份相比都下降了; ③平板电脑4月份的销售额比3月份有所下降; ④今年1~4月中,平板电脑售额最低的是3月. 【变式2】为了了解2022年某地区5万名大、中、小学生3分钟跳绳成绩情况,教育部门从这三类学生群体中各抽取了的学生进行检测.整理样本数据,并结合2018年抽样结果,得到下列统计图. (1)本次检测抽取了大、中、小学生共______名,其中小学生______名; (2)根据抽样的结果,估计2022年该地区5万名大、中、小学生,3分钟跳绳成绩合格的中学生人数为______名; (3)比较2018年与2022年抽样学生3分钟跳绳成绩合格率情况,写出一条正确的结论. 【变式3】为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的时间,设被调查的每名学生每周课外阅读的总时间为x小时,将它分为4个等级:A(),B(),C(),D(),并根据调查结果绘制了如图两幅不完整的统计图: 请你根据统计图的信息,解决下列问题: (1)本次共调查了______名学生; (2)在扇形统计图中,若A等级所占比例为m%,则m的值为_____,等级D所对应的扇形的圆心角为________°; (3)请计算C的学生数目并补全条形统计图; (4)全校1200名学生,估计阅读时间不少于6小时的学生有多少名?
小试牛刀
一、选择题(共5题) 1.记录一个病人体温的变化情况,选用的统计图最好是( ) A.扇形统计图 B.条形统计图 C.折线统计图 D.都可以 2.在条形统计图上________,才会减少直观上的错觉.( ) A.横轴与纵轴都必须从0开始 B.横轴与纵轴都不必从0开始 C.纵轴不必从0开始,横轴必须从0开始 D.横轴不必从0开始,纵轴必须从0开始 3.为迎接党的二十大胜利召开,某校开展了“学党史,悟初心”系列活动.学校对学生参加各项活动的人数进行了调查,并将数据绘制成如下统计图.若参加“书法”的人数为80人,则参加“大合唱”的人数为( ) A.60人 B.100人 C.160人 D.400人 4.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如表所示,则下列说法正确的是( ) 年级七年级八年级九年级合格人数270262254
A.七年级的合格率最高 B.八年级的学生人数为262名 C.八年级的合格率高于全校的合格率 D.九年级的合格人数最少 5.某地区经过三年的乡村振兴建设,农村的经济收入是振兴前的2倍.为更好地了解该地区农村的经济收入变化情况,统计了该地区乡村振兴建设前后农村的经济收入构成比例,绘制了下面的扇形统计图,则下列说法错误的是( ) A.乡村振兴建设后,养殖收入是振兴前的2倍 B.乡村振兴建设后,种植收入减少 C.乡村振兴建设后,其它收入是振兴前的2.5倍 D.乡村振兴建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 二、填空题(共5题) 6.在一个扇形统计图中,表示种植苹果树面积的扇形圆心角为,那么苹果树面积占总种植面积的百分比为 . 7.想了解本周气温的变化情况,最适合采用 统计图.(填“扇形”或“折线”) 8.某中学共40位同学参加了演讲比赛,分段统计参赛同学的成绩,结果如下(分数为整数,满分为100分) 分数段(分〕61~7071~8081~9091~100人数51016
则_________;若制作成扇形统计图,那么81~90分数段所对应扇形的圆心角____°. 9.某校开展“我最喜爱的一项体育运动”调查,每名学生必选且只能选一项.现随机抽查了若干名学生,并将其结果绘制成不完整的条形图和扇形图.在抽查的学生中,喜欢足球运动的人数为______. 10.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初二学生进行了问卷调查,其中一项是疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图不完整,由图中信息可知,下列结论正确的序号 . 本次调查的样本容量是; 选“责任”的有人; 扇形统计图中“生命”所对应的扇形圆心角的大小为; 选“感恩”的人数最多. 三、解答题(共5题) 11.某校开展阳光体育运动,调查了八年级学生喜欢的球类活动(每人只选一项自己最喜欢的球类项目),并将调查情况制成如下统计表和统计图(不完整).请将统计表和统计图补充完整. 球类项目乒乓球篮球足球排球人数30人______人______人______人
12.有人针对公交车上是否主动让座做了一次调查,结果如下: (1)参与本次调查的人数是多少? (2)“从来不让座的人”占调查总人数的百分比是多少? (3)面对以上的调查结果,你还能得到什么结论? 13.由于气温骤变,小米突然感冒了.下面是她的体温记录折线图.回答下列问题: (1)小米的体温最高是 ℃,最低是 ℃. (2)她的体温在哪段时间里下降得最快?在哪段时间里比较稳定?分析其原因. (3)图中的横虚线表示什么? 14.某音像制品店某一天的销售的情况如图: (1)从条形统计图看,民歌类唱片与流行歌曲唱片销售量之比大约是多少?从扇形统计图看呢? (2)要使读者清楚地看出各类音像制品的销售量之比,条形统计图应做怎样的改动? 15.某校举办球赛,分为若干组,其中第一组有A,B,C,D,E五个队.这五个队要进行单循环赛,即每两个队之间要进行一场比赛,每场比赛采用三局两胜制,即三局中胜两局就获胜.每场比赛胜负双方根据比分会获得相应的积分,积分均为正整数.这五个队完成所有比赛后得到如下的积分表. 根据上表回答下列问题: (1)第一组一共进行了 场比赛,A队的获胜场数x为 ; (2)当B队的总积分y=6时,上表中m处应填 ,n处应填 ; (3)写出C队总积分p的所有可能值为: .
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
