2023-2024学年度沪科版数学九年级下册 26.4综合与实践概率在遗传学中的应用课件(共27张PPT)
文档属性
| 名称 | 2023-2024学年度沪科版数学九年级下册 26.4综合与实践概率在遗传学中的应用课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 10:24:59 | ||
图片预览





文档简介
(共27张PPT)
九年级下
沪科版
26.4 综合与实践
概率在遗传学中的应用
1.了解概率在遗传学中的应用.
2.掌握几何概率的计算和应用.
学习目标
重点
重点
阅读下列俗语:
龙生龙,凤生凤,老鼠生的儿子会打洞.
虎父无犬子.
种瓜得瓜,种豆得豆.
这些俗语描述了哪些遗传学现象?
新课引入
奥地利人孟德尔(G.J. Mendel , 1822—1884)通过认真观察遗传现象、设计实验、收集数据、科学分析,成为第一个总结出遗传规律的遗传学家.
他选择豌豆作杂交试验,并注意到不同品种的豌豆具有区别明显的性状(豌豆的花色,种子的形状等都是性状).
所谓性状是指生物的形态、结构和生理等特征.
一 概率在遗传学中的应用
新知学习
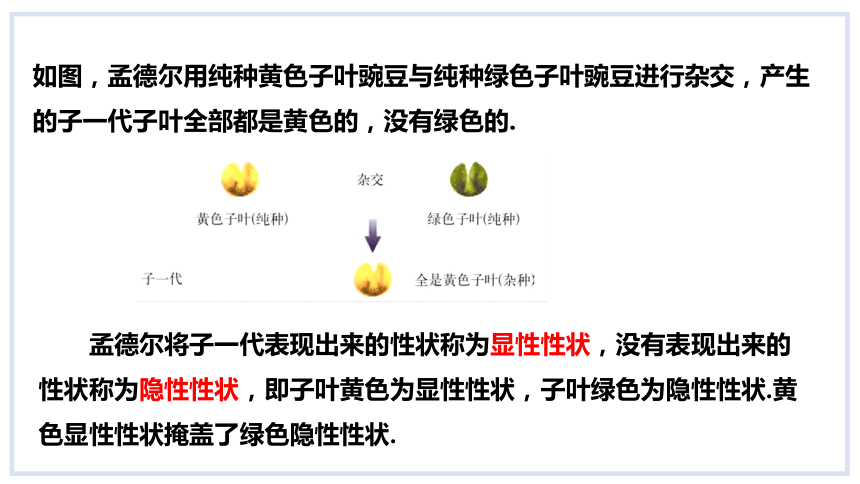
如图,孟德尔用纯种黄色子叶豌豆与纯种绿色子叶豌豆进行杂交,产生的子一代子叶全部都是黄色的,没有绿色的.
孟德尔将子一代表现出来的性状称为显性性状,没有表现出来的性状称为隐性性状,即子叶黄色为显性性状,子叶绿色为隐性性状.黄色显性性状掩盖了绿色隐性性状.
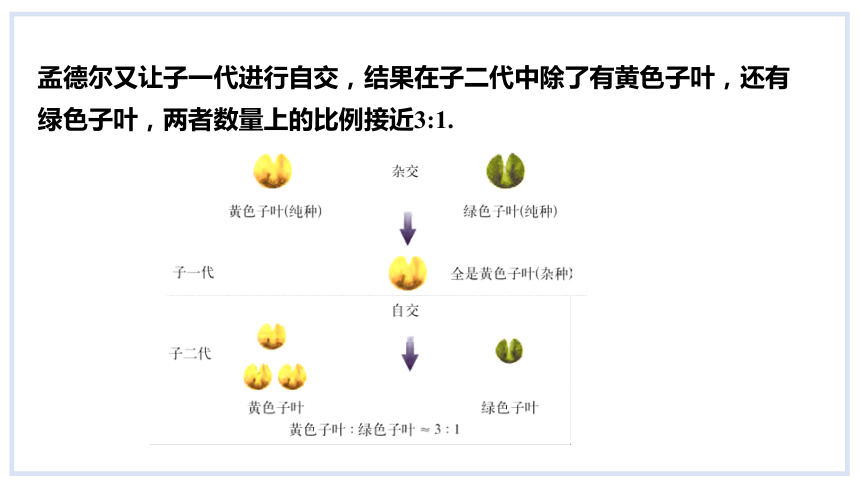
孟德尔又让子一代进行自交,结果在子二代中除了有黄色子叶,还有绿色子叶,两者数量上的比例接近3:1.
为什么在子二代中隐性性状又出现了呢
孟德尔认为,生物的遗传性状是由成对基因(遗传因子)决定的,其中控制显性性状(黄色子叶)的为显性基因(用A表示);控制隐性性状(绿色子叶)的为隐性基因(用a表示).
思考
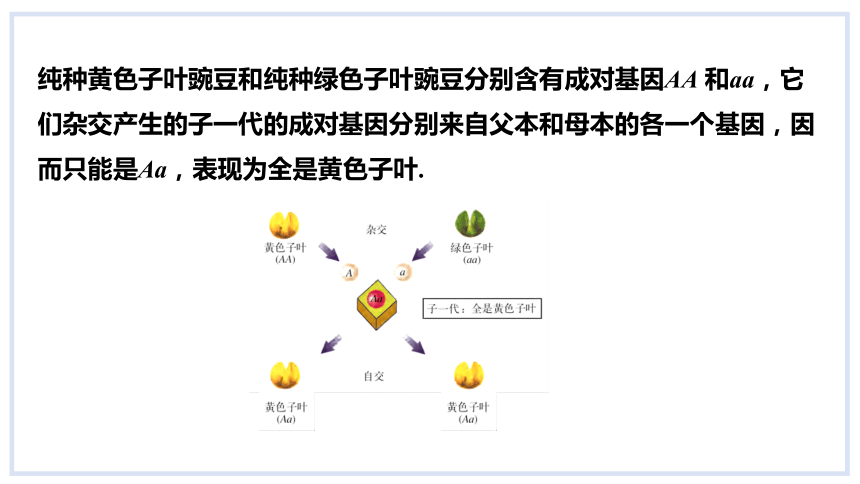
纯种黄色子叶豌豆和纯种绿色子叶豌豆分别含有成对基因AA 和aa,它们杂交产生的子一代的成对基因分别来自父本和母本的各一个基因,因而只能是Aa,表现为全是黄色子叶.
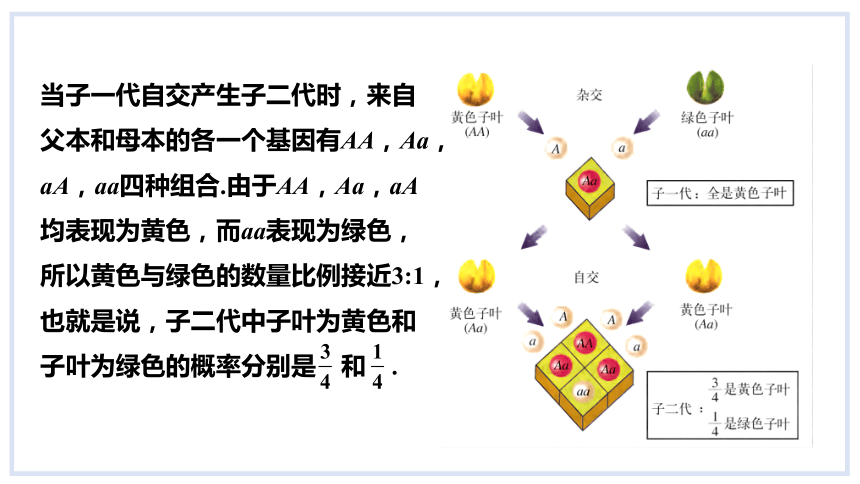
当子一代自交产生子二代时,来自父本和母本的各一个基因有AA,Aa,aA,aa四种组合.由于AA,Aa,aA均表现为黄色,而aa表现为绿色,所以黄色与绿色的数量比例接近3:1,也就是说,子二代中子叶为黄色和子叶为绿色的概率分别是 和 .
人类的遗传病是从上一代(父母)传递给下一代(孩子)而发生的疾病,例如白化病、红绿色盲和高度近视等.了解遗传病的传代规律及出现概率,防止遗传病患儿的出生,是全社会都需要共同关注的问题.
下面用孟德尔发现的遗传规律来探讨白化病的遗传情况.
问题 白化病是一种隐性性状,如果A是正常基因、a是白化病基因,那么携带成对基因Aa的个体的皮肤、头发和眼球的颜色是正常的,而携带成对基因aa 的个体将患有白化病.
(1)设母亲和父亲都携带成对基因Aa,求他们有正常孩子的概率;
Aa
Aa
A
a
AA
Aa
Aa
aa
A
a
正常
正常
正常
白化病
P(有正常孩子)=
(2)设母亲和父亲分别携带成对基因AA和 Aa,求他们有正常孩子的概率和孩子患有白化病的概率;
AA
Aa
A
a
AA
AA
AA
Aa
A
A
正常
正常
正常
正常
P(有正常孩子)=1
P(孩子患白化病)=0
(3)设母亲和父亲分别携带成对基因aa和Aa,求他们有正常孩子的概率和孩子患有白化病的概率.
P(有正常孩子)=
P(孩子患白化病)=
aa
Aa
A
a
Aa
aa
Aa
aa
a
a
正常
白化病
正常
白化病
1.若一对夫妇遗传给子女“有酒窝”和“没有酒窝”这一特征的概率是相等的,该对夫妇有两个子女都“有酒窝”,若允许他们再生一个孩子,则这个孩子“有酒窝”的概率为( )
针对训练
B
A. B. C. D.
二 几何概率的简单计算
这里介绍另外一种基于等可能假设的概率模型.
这种概率模型的基本原理是:设想每个结果是一个点,所有结果的点组成一个区域G,而组成事件A的结果是G中的部分区域g,G,g可以是直线上的线段,也可以是平面或空间的区域.
因此,这种概率可以表示为两个线段的长度之比,或两个平面区域的面积之比,或两个空间区域的体积之比.
例1 某商厦开展“幸运一刻钟”有奖促销活动,办法如下:在营业时间9:00~21:00内随机产生一个15min的时段(如10:36~10:51),该时段内在该商厦购物的顾客可得到与购物款等额的奖券.小明妈妈在商厦购买了一双价格为80元的运动鞋,那么她中奖的概率是多少呢?
商厦一天的营业时间是12h,计720min,那么它的时间长度为720min,可用一条线段AB表示,
设“幸运一刻钟”的起始时刻为点C,终点时刻为点D,则线段CD的时间长度为15min,小明妈妈中奖的概率应为
例2 在图中的正方形中有一内切圆,随机撒一把芝麻,假设每一粒芝麻落在正方形内的每一个点的可能性都是相等的,计算落在圆中的芝麻数与落在正方形中的芝麻数之比,并以此估计圆周率的值.
解 随机撒一把芝麻,每粒芝麻落在正方形内任何一点是等可能的,落在每个区域的芝麻数与这个区域的面积近似成正比,假设正方形的边长为2a,则
如果数出落在每个区域的芝麻数,由上式就能得到 的近似值.比如,向图中的正方形中随机撒400粒芝麻,如果落在圆中的芝麻数是314,那么
通过多次试验可以看出,随着每次试验所撒的芝麻数的增加,圆周率π的近似值精度就越高.
我们也可以用计算机来模拟上述过程,计算π的近似值.
利用几何概率,并通过计算机模拟方法,还可以计算某些不规则图形(图中的区域A)的近似面积:
针对训练
1.现有一款正方形地砖,各边边长均被等分为4份,形成如图所示的图案,若向该地砖上投掷一个沙包,则沙包落在阴影区域的概率是( )
A. B. C. D.
A
1.如图,在△ABC中,D、E分别是AB、BC上的点,且=,DF∥BC,EF∥AB,随机在△ABC内投针,则针扎到阴影区域内的概率为( )
A. B. C. D.
随堂练习
∵DF∥BC,EF∥AB,∴四边形BDFE是平行四边形.
∵=,∴=,
∴=,=()2=,
∴=.
∴P(针扎到阴影区域)==.
【答案】B
2.人的血型常可分为A型、B型、AB型和O型、IAIA和IAi表现为A型,IBIB和IBi表现为B型,IAIB表现为AB型,ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如下表为A(IAi)型父亲和B(IBi)型母亲生下的子女血型基因型表.
(1)求表中O型子女的概率;
IA i
IB IAIB IBi
i IAi ii
IAi
IBi
(2)请仿照这种列表法分析,父母都是AB型,生下子女也是AB型的概率是多少?
IA IB
IA IAIA IAIB
IB IAIB IBIB
IAIB
IAIB
概率的应用
几何概率
的简单计算
根据遗传规律,可以将遗传图解和概率中的树状图或列表,
从而解决遗传中的概率问题.
概率在遗传
学中的应用
课堂小结
九年级下
沪科版
26.4 综合与实践
概率在遗传学中的应用
1.了解概率在遗传学中的应用.
2.掌握几何概率的计算和应用.
学习目标
重点
重点
阅读下列俗语:
龙生龙,凤生凤,老鼠生的儿子会打洞.
虎父无犬子.
种瓜得瓜,种豆得豆.
这些俗语描述了哪些遗传学现象?
新课引入
奥地利人孟德尔(G.J. Mendel , 1822—1884)通过认真观察遗传现象、设计实验、收集数据、科学分析,成为第一个总结出遗传规律的遗传学家.
他选择豌豆作杂交试验,并注意到不同品种的豌豆具有区别明显的性状(豌豆的花色,种子的形状等都是性状).
所谓性状是指生物的形态、结构和生理等特征.
一 概率在遗传学中的应用
新知学习
如图,孟德尔用纯种黄色子叶豌豆与纯种绿色子叶豌豆进行杂交,产生的子一代子叶全部都是黄色的,没有绿色的.
孟德尔将子一代表现出来的性状称为显性性状,没有表现出来的性状称为隐性性状,即子叶黄色为显性性状,子叶绿色为隐性性状.黄色显性性状掩盖了绿色隐性性状.
孟德尔又让子一代进行自交,结果在子二代中除了有黄色子叶,还有绿色子叶,两者数量上的比例接近3:1.
为什么在子二代中隐性性状又出现了呢
孟德尔认为,生物的遗传性状是由成对基因(遗传因子)决定的,其中控制显性性状(黄色子叶)的为显性基因(用A表示);控制隐性性状(绿色子叶)的为隐性基因(用a表示).
思考
纯种黄色子叶豌豆和纯种绿色子叶豌豆分别含有成对基因AA 和aa,它们杂交产生的子一代的成对基因分别来自父本和母本的各一个基因,因而只能是Aa,表现为全是黄色子叶.
当子一代自交产生子二代时,来自父本和母本的各一个基因有AA,Aa,aA,aa四种组合.由于AA,Aa,aA均表现为黄色,而aa表现为绿色,所以黄色与绿色的数量比例接近3:1,也就是说,子二代中子叶为黄色和子叶为绿色的概率分别是 和 .
人类的遗传病是从上一代(父母)传递给下一代(孩子)而发生的疾病,例如白化病、红绿色盲和高度近视等.了解遗传病的传代规律及出现概率,防止遗传病患儿的出生,是全社会都需要共同关注的问题.
下面用孟德尔发现的遗传规律来探讨白化病的遗传情况.
问题 白化病是一种隐性性状,如果A是正常基因、a是白化病基因,那么携带成对基因Aa的个体的皮肤、头发和眼球的颜色是正常的,而携带成对基因aa 的个体将患有白化病.
(1)设母亲和父亲都携带成对基因Aa,求他们有正常孩子的概率;
Aa
Aa
A
a
AA
Aa
Aa
aa
A
a
正常
正常
正常
白化病
P(有正常孩子)=
(2)设母亲和父亲分别携带成对基因AA和 Aa,求他们有正常孩子的概率和孩子患有白化病的概率;
AA
Aa
A
a
AA
AA
AA
Aa
A
A
正常
正常
正常
正常
P(有正常孩子)=1
P(孩子患白化病)=0
(3)设母亲和父亲分别携带成对基因aa和Aa,求他们有正常孩子的概率和孩子患有白化病的概率.
P(有正常孩子)=
P(孩子患白化病)=
aa
Aa
A
a
Aa
aa
Aa
aa
a
a
正常
白化病
正常
白化病
1.若一对夫妇遗传给子女“有酒窝”和“没有酒窝”这一特征的概率是相等的,该对夫妇有两个子女都“有酒窝”,若允许他们再生一个孩子,则这个孩子“有酒窝”的概率为( )
针对训练
B
A. B. C. D.
二 几何概率的简单计算
这里介绍另外一种基于等可能假设的概率模型.
这种概率模型的基本原理是:设想每个结果是一个点,所有结果的点组成一个区域G,而组成事件A的结果是G中的部分区域g,G,g可以是直线上的线段,也可以是平面或空间的区域.
因此,这种概率可以表示为两个线段的长度之比,或两个平面区域的面积之比,或两个空间区域的体积之比.
例1 某商厦开展“幸运一刻钟”有奖促销活动,办法如下:在营业时间9:00~21:00内随机产生一个15min的时段(如10:36~10:51),该时段内在该商厦购物的顾客可得到与购物款等额的奖券.小明妈妈在商厦购买了一双价格为80元的运动鞋,那么她中奖的概率是多少呢?
商厦一天的营业时间是12h,计720min,那么它的时间长度为720min,可用一条线段AB表示,
设“幸运一刻钟”的起始时刻为点C,终点时刻为点D,则线段CD的时间长度为15min,小明妈妈中奖的概率应为
例2 在图中的正方形中有一内切圆,随机撒一把芝麻,假设每一粒芝麻落在正方形内的每一个点的可能性都是相等的,计算落在圆中的芝麻数与落在正方形中的芝麻数之比,并以此估计圆周率的值.
解 随机撒一把芝麻,每粒芝麻落在正方形内任何一点是等可能的,落在每个区域的芝麻数与这个区域的面积近似成正比,假设正方形的边长为2a,则
如果数出落在每个区域的芝麻数,由上式就能得到 的近似值.比如,向图中的正方形中随机撒400粒芝麻,如果落在圆中的芝麻数是314,那么
通过多次试验可以看出,随着每次试验所撒的芝麻数的增加,圆周率π的近似值精度就越高.
我们也可以用计算机来模拟上述过程,计算π的近似值.
利用几何概率,并通过计算机模拟方法,还可以计算某些不规则图形(图中的区域A)的近似面积:
针对训练
1.现有一款正方形地砖,各边边长均被等分为4份,形成如图所示的图案,若向该地砖上投掷一个沙包,则沙包落在阴影区域的概率是( )
A. B. C. D.
A
1.如图,在△ABC中,D、E分别是AB、BC上的点,且=,DF∥BC,EF∥AB,随机在△ABC内投针,则针扎到阴影区域内的概率为( )
A. B. C. D.
随堂练习
∵DF∥BC,EF∥AB,∴四边形BDFE是平行四边形.
∵=,∴=,
∴=,=()2=,
∴=.
∴P(针扎到阴影区域)==.
【答案】B
2.人的血型常可分为A型、B型、AB型和O型、IAIA和IAi表现为A型,IBIB和IBi表现为B型,IAIB表现为AB型,ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如下表为A(IAi)型父亲和B(IBi)型母亲生下的子女血型基因型表.
(1)求表中O型子女的概率;
IA i
IB IAIB IBi
i IAi ii
IAi
IBi
(2)请仿照这种列表法分析,父母都是AB型,生下子女也是AB型的概率是多少?
IA IB
IA IAIA IAIB
IB IAIB IBIB
IAIB
IAIB
概率的应用
几何概率
的简单计算
根据遗传规律,可以将遗传图解和概率中的树状图或列表,
从而解决遗传中的概率问题.
概率在遗传
学中的应用
课堂小结
