新人教版数学七年级下册 第五章相交线与平行线5.3.1《平行线的性质》课时练习.doc
文档属性
| 名称 | 新人教版数学七年级下册 第五章相交线与平行线5.3.1《平行线的性质》课时练习.doc |

|
|
| 格式 | doc | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-10 00:00:00 | ||
图片预览


文档简介
人教版数学七年级下册5.3.1平行线的性质同步练习
一.单选题
1.如图,AB//CD,EF分别为交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质
解析:
解答:∵AB∥CD,∠1=50°,
∴∠FEB=∠1=50°.
∴∠2=180°-∠FEB=130°.
故选择C
分析:两直线平行同位角相等.
2.如图,直线a∥b,若∠1=120°,则∠2等于( )
A.60° B.80° C.120° D.150°
( http: / / www.21cnjy.com )
答案:A
知识点:平行线的性质
解析:
解答:∵a∥b,
∴∠1+∠2=180°
∴∠2=60°
故选A
分析:两直线平行同旁内角互补.
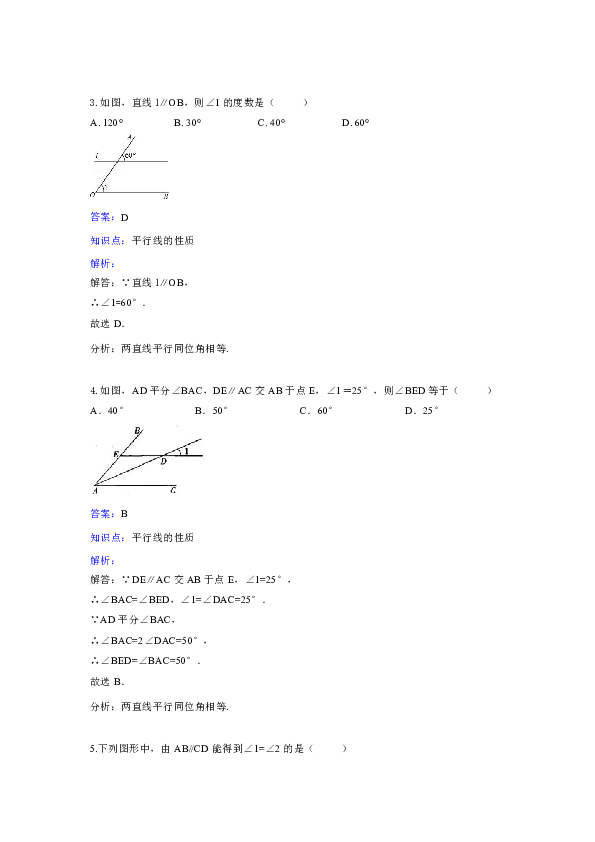
3.如图,直线l∥OB,则∠1的度数是( )
A. 120° B. 30° C. 40° D. 60°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质
解析:
解答:∵直线l∥OB,
∴∠1=60°.
故选D.
分析:两直线平行同位角相等.
4.如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )
A.40° B.50° C.60° D.25°
( http: / / www.21cnjy.com )
答案:B
知识点:平行线的性质
解析:
解答:∵DE∥AC交AB于点E,∠1=25°,
∴∠BAC=∠BED,∠1=∠DAC=25°.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∴∠BED=∠BAC=50°.
故选B.
分析:两直线平行同位角相等.
5.下列图形中,由AB//CD能得到∠1=∠2的是( )
( http: / / www.21cnjy.com )
答案:B
知识点:平行线的性质
解析:
解答:根据平行线性质判断每一个选项,答案是B.
分析:A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
( http: / / www.21cnjy.com )
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选B.
6.如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )
A.60° B.80° C.120° D.150°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质;对顶角.
解析:
解答:根据对顶角相等和两直线平行同位角相等可得∠1=∠2=120°,故选C.
分析:两直线平行同位角相等,对顶角相等.
7.如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A. 100° B. 110° C. 120° D. 130°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质.
解析:
解答:∵∠3=90°﹣40°=50°,a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选D.
分析:两直线平行同旁内角互补.
8.如图, AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质.
解析:
解答:由两直线平行,同位角相等,知∠A=∠2=50°,
∠1=∠A=50°,选C。
分析:两直线平行同位角相等.
9.如图,AF∥CD,BC平分∠ACD,B ( http: / / www.21cnjy.com )D平分∠EBF,且BC⊥BD.下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质;角平分线的定义;余角和补角.
解析:
解答:根据平行线的性质、角平分线的定义、余角的定义作答,选择C.
故选C.
分析:①∵BC⊥BD,
∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,
又∵BD平分∠EBF,
∴∠DBE=∠DBF,
∴∠ABC=∠CBE,
即BC平分∠ABE,正确;
②由AB∥CE ,BC 平分∠ABE、∠ACE易证∠ACB=∠CBE,∴AC∥BE正确;
③∵BC⊥AD,∴∠BCD+∠D=90°正确;
④无法证明∠DBF=60°,故错误.
10.如图,OP∥QR∥ST,则下列各式中正确的是( )
A. ∠1+∠2+∠3=180° B. ∠1+∠2﹣∠3=90°
C. ∠1﹣∠2+∠3=90° D. ∠2+∠3﹣∠1=180°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质,三角形外角的性质;余角和补角
解析:
解答:延长TS,由OP∥QR∥ST可知∠2=∠4,∠ESR=180°﹣∠3,再由三角形外角的性质即可得出结论.解:延长TS,2·1·c·n·j·y
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠ESR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
故选D.
分析:根据两直线平行同位角相等;三角形外角性质;邻补角.
11、两条不平行的直线被第三条直线所截,下列说法可能成立的是( )
A、同位角相等 B、内错角相等
C、同旁内角相等 D、同旁内角互补
答案:C
知识点:平行线的性质.
解析:
解答:根据平行性质A、B、D可排除,故选择C.
分析:两直线平行同位角相等,内错角相等,同旁内角互补.
12、两条直线被第三条直线所截,那么下面说法正确的上是( )
A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上都不对
答案:D
知识点:平行线的性质.
解析:
解答:根据平行性质A、B、C可排除,故选择D.
分析:两直线平行同位角相等,内错角相等,同旁内角互补.
13、如果∠A和∠B是两平行直线中的同旁内角,且∠A比∠B的2倍少30 ,则∠B的度数是( )
A、30 B、70 C、110 D、30 或70
答案:B
知识点:平行线的性质.
解析:
解答:∵∠A+∠B=180°,∠A=2∠B-30°。
∴∠B=70°
分析:两直线平行同旁内角互补.
14、如图,直线c截二平行直线a、b,则下列式子中一定成立的是( )
A、∠1=∠5 B、∠1=∠4 C、∠2=∠3 D、∠1=∠2
答案:A
知识点:平行线的性质.
解析:
解答:根据题意可以分析出∠1=∠3=∠5,∠4=∠2,故选择A
分析:本提考察平行线性质应用.
15、如图,AB∥CD,直线EF分别交AB、CD于E、F两点,若∠FEB=110°,则∠EFD等于( )
A、50° B、60° C、70° D、110°
答案:C
知识点:平行线的性质.
解析:
解答:∵∠FEB+∠EFD=180°,
∴∠EFD=70°,故选择C
分析:两直线平行同旁内角互补.
二.填空题
16.如图,已知∠1=∠2,∠3=73°,则∠4的度数为 度.
( http: / / www.21cnjy.com )
答案:107
知识点:平行线的性质;对顶角.
解析:
解答:∵∠1=∠2,
∴a∥b,
∴∠5+∠3=180°,
∵∠4=∠5,∠3=73°,
∴∠4+∠3=180°,
则∠4=107°.
故答案为:107
分析:根据已知一对同位 ( http: / / www.21cnjy.com )角相等,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到一对角互补,再利用对顶角相等即可确定出∠4的度数.
17.如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D= 度.
答案:35
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AD∥BC, ∠A=110°,∴∠ABC=70°,∵BD平分∠ABC, ∴∠DBC=35°
∴AD∥BC, ∴∠D=∠DBC=35°.
分析:根据已知两直线平行,可得同旁内角互补确定∠ABC,再利用角平分线即可确定出∠DCB的度数,最后根据两直线平行内错角相等即得∠D.
18.将一副三角板如图放置。若AE∥BC,则∠AFD= °。
( http: / / www.21cnjy.com )
答案:75
知识点:平行线的性质;三角形的外角性质.
解析:
解答:∵AE∥BC,∴∠EAF=∠C=30°。
又∵∠E=45°,∴∠AFD=∠EAF+∠E=30°+45°=75°
分析:根据已知两直线平行,可得内错角相等确定∠EAF,再利用三角形外角即可确定出∠AFD的度数.
19.如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= °.
( http: / / www.21cnjy.com )
答案:70
知识点:平行线的性质.
解析:
解答:∵DE∥AC,
∴∠C=∠1=70°,
∵AF∥BC,
∴∠2=∠C=70°.
分析:根据两直线平行,同位角相等可得∠C=∠1,再根据两直线平行,内错角相等可得∠2=∠C.
20.如图,AB∥CD,OE平分∠BOC, ( http: / / www.21cnjy.com )OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有___________(填序号)21·
( http: / / www.21cnjy.com )
答案:①②③
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AB∥CD,
∴∠ABO=∠BOD=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠BOE=70°;所以①正确;
∵OF⊥OE,
∴∠E OF=90°,
∴∠ BOF=90°﹣70°=20°,
∴∠BOF=∠BOD,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=20°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=70°﹣∠POE=50°,
而∠DOF=20 °,所以④错误.
故答案为①②③.
( http: / / www.21cnjy.com )
分析:由于AB∥ CD,则∠ABO= ( http: / / www.21cnjy.com )∠BOD=40°,利用平角等于得到∠BOC=140°,再根据角平分线定义得到∠BOE=70°;利用OF⊥OE,可计算出∠BOF=20°,则∠BOF=∠BOD,即OF平分∠BOD; 利用OP⊥CD,可计算出∠POE=20°,则∠POE=∠BOF; 根据∠POB=70°﹣∠POE=50°,∠DOF=20°,可知④不正确.
三.解答题
21. 如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
证明:∵∠A=∠F(已知)
∴AC∥ ( )
∴∠D=∠1( )
又∵∠C=∠D(已知)
∴∠1= ( )
∴BD∥CE( )
答案:DF、内错角相等,两直线平行、两直线平行,内错角相等、∠C、等量代换、同位角相等,两直线平行.
知识点:平行线的性质与判定.
解析:
解答:∵∠A=∠F(已知)
∴AC∥DF(内错角相等,两直线平行)
∴∠D=∠1(两直线平行,内错角相等)
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE(同位角相等,两直线平行).
分析:由已知一对内错角相等 ( http: / / www.21cnjy.com )得到AC与DF平行,利用两直线平行同位角相等得到一对角相等,再由已知另一对角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.2
22.已知:如图所示,. l1∥l2,∠1+∠2=180°
(1)求证:∠1=∠3.
(2)求∠2+∠4的度数.
( http: / / www.21cnjy.com )
答案:(1)∵l1∥l2 ∴∠2+∠3=18 ( http: / / www.21cnjy.com )0°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等).
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)
知识点:平行线的性质;余角和补角.
解析:
解答:(1)∵l1∥l2 ∴∠2+∠3=18 ( http: / / www.21cnjy.com )0°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等).
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)
分析:根据两直线平行内错角相等、同旁内角互补,可得本题答案.
23.如图,AB∥CD,∠ACB=90°,∠ACD=55°,求∠B的度数.
( http: / / www.21cnjy.com )
答案:∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180°﹣∠A=90°﹣55°=35°.
知识点:平行线的性质.
解析:
∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180°﹣∠A=90°﹣55°=35°.
分析:根据两直线平行内错角相等,可得本题答案.
24.如图,AD∥BC,AD平分∠EAC,你能确定∠B与∠C的数量关系吗?请说明理由.
( http: / / www.21cnjy.com )
答案:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
知识点:平行线的性质;角平分线的定义.
解析:
解答:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
分析:根据两直线平行内错角相等、同位角相等,可得本题答案.
25.如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
( http: / / www.21cnjy.com )
答案:125°
∵AB∥CD,∠B=110°,
∴∠BDC=180°-110°=70°,
∵DA平分∠BDC,
∴∠ADC=35°.
∵DE⊥AD于D,
所以∠CDE=90°-∠ADC=55°,
∴∠BDE=∠BDC+∠ADC=125°
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AB∥CD,∠B=110°,
∴∠BDC=180°-110°=70°,
∵DA平分∠BDC,
∴∠ADC=35°.
∵DE⊥AD于D,
所以∠CDE=90°-∠ADC=55°,
∴∠BDE=∠BDC+∠ADC=125°
分析:根据两直线平行同旁内角互补,可得本题答案.
一.单选题
1.如图,AB//CD,EF分别为交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质
解析:
解答:∵AB∥CD,∠1=50°,
∴∠FEB=∠1=50°.
∴∠2=180°-∠FEB=130°.
故选择C
分析:两直线平行同位角相等.
2.如图,直线a∥b,若∠1=120°,则∠2等于( )
A.60° B.80° C.120° D.150°
( http: / / www.21cnjy.com )
答案:A
知识点:平行线的性质
解析:
解答:∵a∥b,
∴∠1+∠2=180°
∴∠2=60°
故选A
分析:两直线平行同旁内角互补.
3.如图,直线l∥OB,则∠1的度数是( )
A. 120° B. 30° C. 40° D. 60°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质
解析:
解答:∵直线l∥OB,
∴∠1=60°.
故选D.
分析:两直线平行同位角相等.
4.如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )
A.40° B.50° C.60° D.25°
( http: / / www.21cnjy.com )
答案:B
知识点:平行线的性质
解析:
解答:∵DE∥AC交AB于点E,∠1=25°,
∴∠BAC=∠BED,∠1=∠DAC=25°.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∴∠BED=∠BAC=50°.
故选B.
分析:两直线平行同位角相等.
5.下列图形中,由AB//CD能得到∠1=∠2的是( )
( http: / / www.21cnjy.com )
答案:B
知识点:平行线的性质
解析:
解答:根据平行线性质判断每一个选项,答案是B.
分析:A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
( http: / / www.21cnjy.com )
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选B.
6.如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )
A.60° B.80° C.120° D.150°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质;对顶角.
解析:
解答:根据对顶角相等和两直线平行同位角相等可得∠1=∠2=120°,故选C.
分析:两直线平行同位角相等,对顶角相等.
7.如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A. 100° B. 110° C. 120° D. 130°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质.
解析:
解答:∵∠3=90°﹣40°=50°,a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选D.
分析:两直线平行同旁内角互补.
8.如图, AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质.
解析:
解答:由两直线平行,同位角相等,知∠A=∠2=50°,
∠1=∠A=50°,选C。
分析:两直线平行同位角相等.
9.如图,AF∥CD,BC平分∠ACD,B ( http: / / www.21cnjy.com )D平分∠EBF,且BC⊥BD.下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
答案:C
知识点:平行线的性质;角平分线的定义;余角和补角.
解析:
解答:根据平行线的性质、角平分线的定义、余角的定义作答,选择C.
故选C.
分析:①∵BC⊥BD,
∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,
又∵BD平分∠EBF,
∴∠DBE=∠DBF,
∴∠ABC=∠CBE,
即BC平分∠ABE,正确;
②由AB∥CE ,BC 平分∠ABE、∠ACE易证∠ACB=∠CBE,∴AC∥BE正确;
③∵BC⊥AD,∴∠BCD+∠D=90°正确;
④无法证明∠DBF=60°,故错误.
10.如图,OP∥QR∥ST,则下列各式中正确的是( )
A. ∠1+∠2+∠3=180° B. ∠1+∠2﹣∠3=90°
C. ∠1﹣∠2+∠3=90° D. ∠2+∠3﹣∠1=180°
( http: / / www.21cnjy.com )
答案:D
知识点:平行线的性质,三角形外角的性质;余角和补角
解析:
解答:延长TS,由OP∥QR∥ST可知∠2=∠4,∠ESR=180°﹣∠3,再由三角形外角的性质即可得出结论.解:延长TS,2·1·c·n·j·y
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠ESR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
故选D.
分析:根据两直线平行同位角相等;三角形外角性质;邻补角.
11、两条不平行的直线被第三条直线所截,下列说法可能成立的是( )
A、同位角相等 B、内错角相等
C、同旁内角相等 D、同旁内角互补
答案:C
知识点:平行线的性质.
解析:
解答:根据平行性质A、B、D可排除,故选择C.
分析:两直线平行同位角相等,内错角相等,同旁内角互补.
12、两条直线被第三条直线所截,那么下面说法正确的上是( )
A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上都不对
答案:D
知识点:平行线的性质.
解析:
解答:根据平行性质A、B、C可排除,故选择D.
分析:两直线平行同位角相等,内错角相等,同旁内角互补.
13、如果∠A和∠B是两平行直线中的同旁内角,且∠A比∠B的2倍少30 ,则∠B的度数是( )
A、30 B、70 C、110 D、30 或70
答案:B
知识点:平行线的性质.
解析:
解答:∵∠A+∠B=180°,∠A=2∠B-30°。
∴∠B=70°
分析:两直线平行同旁内角互补.
14、如图,直线c截二平行直线a、b,则下列式子中一定成立的是( )
A、∠1=∠5 B、∠1=∠4 C、∠2=∠3 D、∠1=∠2
答案:A
知识点:平行线的性质.
解析:
解答:根据题意可以分析出∠1=∠3=∠5,∠4=∠2,故选择A
分析:本提考察平行线性质应用.
15、如图,AB∥CD,直线EF分别交AB、CD于E、F两点,若∠FEB=110°,则∠EFD等于( )
A、50° B、60° C、70° D、110°
答案:C
知识点:平行线的性质.
解析:
解答:∵∠FEB+∠EFD=180°,
∴∠EFD=70°,故选择C
分析:两直线平行同旁内角互补.
二.填空题
16.如图,已知∠1=∠2,∠3=73°,则∠4的度数为 度.
( http: / / www.21cnjy.com )
答案:107
知识点:平行线的性质;对顶角.
解析:
解答:∵∠1=∠2,
∴a∥b,
∴∠5+∠3=180°,
∵∠4=∠5,∠3=73°,
∴∠4+∠3=180°,
则∠4=107°.
故答案为:107
分析:根据已知一对同位 ( http: / / www.21cnjy.com )角相等,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到一对角互补,再利用对顶角相等即可确定出∠4的度数.
17.如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D= 度.
答案:35
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AD∥BC, ∠A=110°,∴∠ABC=70°,∵BD平分∠ABC, ∴∠DBC=35°
∴AD∥BC, ∴∠D=∠DBC=35°.
分析:根据已知两直线平行,可得同旁内角互补确定∠ABC,再利用角平分线即可确定出∠DCB的度数,最后根据两直线平行内错角相等即得∠D.
18.将一副三角板如图放置。若AE∥BC,则∠AFD= °。
( http: / / www.21cnjy.com )
答案:75
知识点:平行线的性质;三角形的外角性质.
解析:
解答:∵AE∥BC,∴∠EAF=∠C=30°。
又∵∠E=45°,∴∠AFD=∠EAF+∠E=30°+45°=75°
分析:根据已知两直线平行,可得内错角相等确定∠EAF,再利用三角形外角即可确定出∠AFD的度数.
19.如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= °.
( http: / / www.21cnjy.com )
答案:70
知识点:平行线的性质.
解析:
解答:∵DE∥AC,
∴∠C=∠1=70°,
∵AF∥BC,
∴∠2=∠C=70°.
分析:根据两直线平行,同位角相等可得∠C=∠1,再根据两直线平行,内错角相等可得∠2=∠C.
20.如图,AB∥CD,OE平分∠BOC, ( http: / / www.21cnjy.com )OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有___________(填序号)21·
( http: / / www.21cnjy.com )
答案:①②③
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AB∥CD,
∴∠ABO=∠BOD=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠BOE=70°;所以①正确;
∵OF⊥OE,
∴∠E OF=90°,
∴∠ BOF=90°﹣70°=20°,
∴∠BOF=∠BOD,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=20°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=70°﹣∠POE=50°,
而∠DOF=20 °,所以④错误.
故答案为①②③.
( http: / / www.21cnjy.com )
分析:由于AB∥ CD,则∠ABO= ( http: / / www.21cnjy.com )∠BOD=40°,利用平角等于得到∠BOC=140°,再根据角平分线定义得到∠BOE=70°;利用OF⊥OE,可计算出∠BOF=20°,则∠BOF=∠BOD,即OF平分∠BOD; 利用OP⊥CD,可计算出∠POE=20°,则∠POE=∠BOF; 根据∠POB=70°﹣∠POE=50°,∠DOF=20°,可知④不正确.
三.解答题
21. 如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
证明:∵∠A=∠F(已知)
∴AC∥ ( )
∴∠D=∠1( )
又∵∠C=∠D(已知)
∴∠1= ( )
∴BD∥CE( )
答案:DF、内错角相等,两直线平行、两直线平行,内错角相等、∠C、等量代换、同位角相等,两直线平行.
知识点:平行线的性质与判定.
解析:
解答:∵∠A=∠F(已知)
∴AC∥DF(内错角相等,两直线平行)
∴∠D=∠1(两直线平行,内错角相等)
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE(同位角相等,两直线平行).
分析:由已知一对内错角相等 ( http: / / www.21cnjy.com )得到AC与DF平行,利用两直线平行同位角相等得到一对角相等,再由已知另一对角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.2
22.已知:如图所示,. l1∥l2,∠1+∠2=180°
(1)求证:∠1=∠3.
(2)求∠2+∠4的度数.
( http: / / www.21cnjy.com )
答案:(1)∵l1∥l2 ∴∠2+∠3=18 ( http: / / www.21cnjy.com )0°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等).
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)
知识点:平行线的性质;余角和补角.
解析:
解答:(1)∵l1∥l2 ∴∠2+∠3=18 ( http: / / www.21cnjy.com )0°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等).
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)
分析:根据两直线平行内错角相等、同旁内角互补,可得本题答案.
23.如图,AB∥CD,∠ACB=90°,∠ACD=55°,求∠B的度数.
( http: / / www.21cnjy.com )
答案:∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180°﹣∠A=90°﹣55°=35°.
知识点:平行线的性质.
解析:
∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180°﹣∠A=90°﹣55°=35°.
分析:根据两直线平行内错角相等,可得本题答案.
24.如图,AD∥BC,AD平分∠EAC,你能确定∠B与∠C的数量关系吗?请说明理由.
( http: / / www.21cnjy.com )
答案:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
知识点:平行线的性质;角平分线的定义.
解析:
解答:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
分析:根据两直线平行内错角相等、同位角相等,可得本题答案.
25.如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
( http: / / www.21cnjy.com )
答案:125°
∵AB∥CD,∠B=110°,
∴∠BDC=180°-110°=70°,
∵DA平分∠BDC,
∴∠ADC=35°.
∵DE⊥AD于D,
所以∠CDE=90°-∠ADC=55°,
∴∠BDE=∠BDC+∠ADC=125°
知识点:平行线的性质;角平分线的定义.
解析:
解答:∵AB∥CD,∠B=110°,
∴∠BDC=180°-110°=70°,
∵DA平分∠BDC,
∴∠ADC=35°.
∵DE⊥AD于D,
所以∠CDE=90°-∠ADC=55°,
∴∠BDE=∠BDC+∠ADC=125°
分析:根据两直线平行同旁内角互补,可得本题答案.
