“勾股定理的应用”说课稿(陕西省渭南市大荔县)
文档属性
| 名称 | “勾股定理的应用”说课稿(陕西省渭南市大荔县) |
|
|
| 格式 | rar | ||
| 文件大小 | 39.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-01 22:34:00 | ||
图片预览



文档简介
大荔县数学教学展评活动
说课稿
教 材: 人教版新教材八年级(下)
课 题: §18.1勾股定理(4)
教 师: 李 珍
朝 邑 镇 初 级 中 学
Chao yi Zhen Chu Ji Zhong Xue
二OO九年三月
“勾股定理的应用”说课稿
朝邑初中 李珍
1、 说教材分析:
本课时是人教版八年级(下)数学第十八章勾股定理第一节第四课时内容,是在掌握勾股定理的基础上对勾股定理的应用之一。
勾股定理是我国传统数学中的一大法宝。在我国几何体系中占有十分独特的地位。而且它也是中国两千多年来数学发展的一个重要的生长点。中国数学中的精髓,他为我们提供了直角三角形的三边的数量关系,既是直角三角形性质的拓展,又是后续学习解直角三角形的基础,他紧密联系了数学中最基本的两个量——数和形,能够把形(直角三角形中一个角是直角)转化成数量关系(三边之间满足),既是数形结合的典范,又体现了转化和方程思想。这些成果广泛应用于数学和实际生活的各个方面,教材在编写时注意培养学生的动手操作能力和分析能力,使学生获得较为直观的印象,通过联系和比较,了解勾股定理在实际生活的广泛应用。
(一)知识与技能目标:
1、运用勾股定理,能在数轴上找到表示无理数的点,进一步领会数形结合的思想。
2、进一步学习将实际问题转化为直角三角形的数学模型,并能用勾股定理解决简单的实际问题。
3、体验数学学习的乐趣,形成积极参与数学活动的意识,再一次感受勾股定理的应用价值。
旨在培养学生探究、创造、实践的能力。
(二)过程与方法目标;
1、经历在数轴上寻找表示无理数的点的过程中,发展学生灵活运用勾股定理解决实际问题的能力。
2、在运用勾股定理解决实际问题的过程中,体验解决问题的策略,发展学生的动手操作能力和创新精神。
3、在解决实际问题的过程中,学会与人合作,并能与他人交流思维过程和结果,形成反思的意识。
旨在培养学生数形结合能力动手操作能力和创新精神。
(三)情感目标:
1、在数轴上寻找表示无理数的点的过程中,体验勾股定理的重要作用,使他们获得成功的体验,锻炼克服困难的意志,建立自信心。
2、在解决实际问题的过程中,形成实事求是的态度以及进行质疑和独立思考的习惯。
旨在让学生体会勾股定理在生活中的广泛应用;体验数学学习的乐趣,提高应用数学的意识。
(四)教学重点难点:
1、重点:在数轴上寻找表示、、------这样的表示无理数的点。
2、难点:利用勾股定理寻找直角三角形中长度为无理数的线段。
3、教学关键:在现实情境中捕抓直角三角形,确定好直角三角形之后,再应用勾股定理。
(五)教学设备或教辅工具:
长方形图画纸一张、剪刀、画图工具、多媒体课件等。
二、说教法、学法:
(一) 教法:
“教必有法,而教无定法”,只有方法恰当,教学才会有效。根据本课内容特点和八年级学生思维活动特点,我采用了引导发现法,自主学习法。
在教学设计过程中力求让学生参与知识的发现过程,体现以学生为主体,以促进学生发展为本的教学理念,变教师知识的传授者的身份为学生自主探求知识的引导者、指导者、合作者。在学生课下收集了资料后,课上给予学生足够的时间展示、互相讲解,并鼓励学生加入自己的想法,提出独特、创新的方法在数轴上找到无理数,从而锻炼学生的思维、激发学生的创造性,优化课堂教学,努力做到由传统的数学课堂向实验课堂转变,使学生真正成为学习的主人。基于以上设计,预期本节课能收到良好的教学效果。
(二)学法:
学生都渴望与他人交流,合作探究可使学生感受到合作的重要和团队的精神力量,增强集体意识,所以本课采用小组合作的学习方式,让学生遵循“观察——猜想——验证——归纳——反馈——实践”的主线进行学习。
三、说教学程序:
本节内容的教学主要体现在学生的动手,动脑方面,根据学生的认知规律和学习心理,教学程序设置如下:
(一)创设情景,提出问题
投影出示:一张美丽的海螺图案:
设问1:同学们,你们知道吗?在数学中也有这样一幅美丽的“螺形”图案呢!学生欣赏“数学海螺(螺形图)”
设计说明:动态的多媒体课件突出了“形”的相似之处,激发学生强烈的探究欲望。
设问2.:他是怎样画出来的?是依据什么数学知识来画的?与同伴交流你的看法。
设计说明:引导学生主动探究,培养与人合作交流的能力。
(二)探索分析,解决问题:
通过观察讨论发现:
画图的依据:勾股定理。
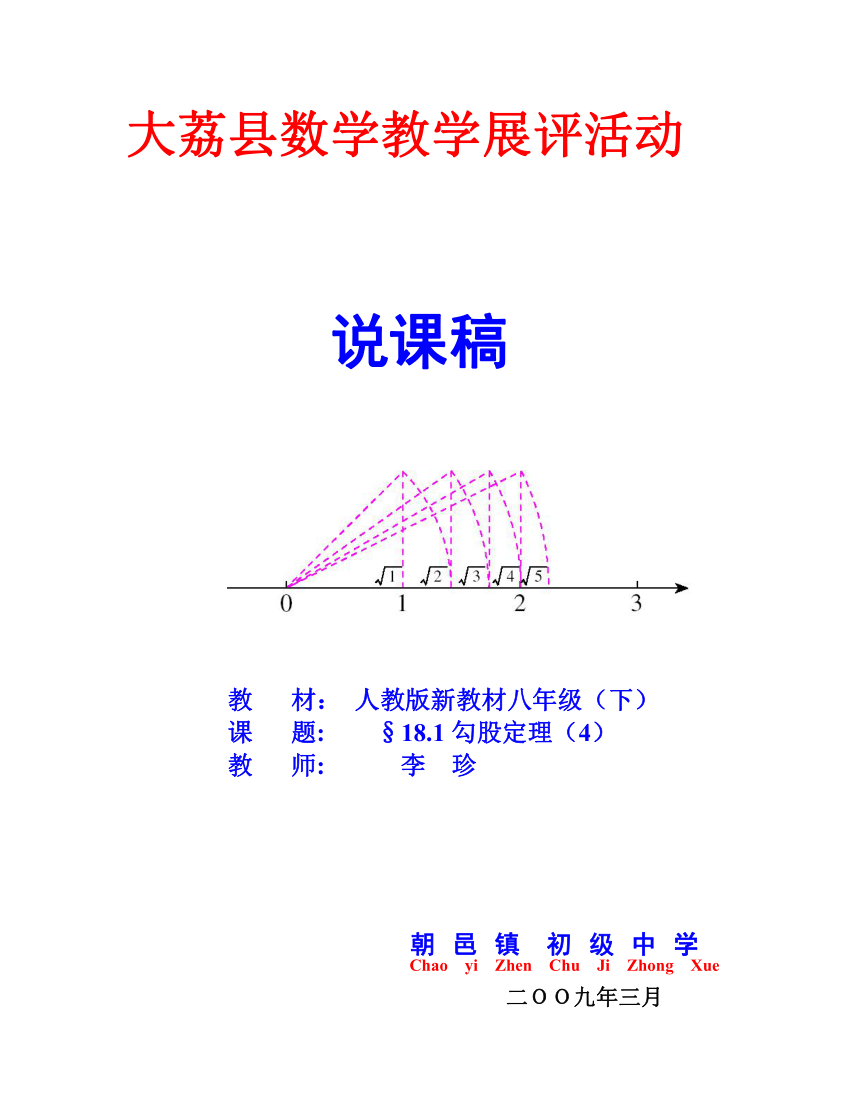
画图的方法:先构造出长为1的等腰直角三角形,并以前一个三角形的斜边和长度为1的线段为直角边向外画直角三角形,这样就可以依次画出长度为(n是正整数)的线段。
设计说明:培养学生有条理的表达的能力。
设问3:如果我们将最初的等腰直角三角形画在数轴上(以数轴的单位1为直角边长),你能有什么新的发现?
设计说明:知识的迁移在不知不觉中完成。
设问4:你能找到,,,------,在数轴上的简便画法吗?
学生小组讨论,发现:
,,,,------,可以构造直角三角形来画图。(教师板演在数轴上画出相应的点的画图过程)
设计说明:规范画图语言和作图方法。
(三)巩固新知,反馈调控
画一画:课本第69页练习第1题。
(四)深入探究,提出问题
问题:有一个圆柱,高12cm,底面半径3cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的C点处的食物,沿圆柱侧面爬行的最短路程是多少?(π的值取3)①学生取出自制圆柱,,尝试从A点到C点沿圆柱侧面画出几条路线.思考:那条路线最短 ②如图,将圆柱侧面剪开展成一个长方形,从A点到C点的最短路线是什么 你画得对吗 ③蚂蚁从A点出发,想吃到C点处的食物,它沿圆柱侧面爬行的最短路线是什么
设计说明:趣题设置,激发兴趣。
(五)小结:
你对本节内容有哪些认识?会利用勾股定理得到一些无理数并理解数轴上的点与实数一一对应。
设计说明:这种形式的小结,激发了学生主动参与意识,调动了学生的学习兴趣,为每一位学生都创造了在数学学习活动中获得成功的体验机会,尊重学生的个体差异,满足学生多样化的学习需要,从而使小结活动不流于形式而具有时效性,为学生提供了更好的学习空间以梳理自己在本节课中的收获。
(六)作业设计:
1.必做题:A课本70页习题18.1第6 第12题;课本81页复习题18第7第8题。
B请你举一个生活中的实例,并利用勾股定理解决它。
旨在突破本节课的教学难点,通过教师的指导、学生间的合作互助,使所有的学生都获得问题的解决;
2.选做题:课本第71页习题18.1第11题。
旨在调动学生进一步参与教学活动的积极性;
3.备选题:古算趣题:“执竿进屋”
笨人执竿要进屋,无奈门框拦住竹。
横多四尺竖多二,没法急的放声哭。
有个邻居聪明着,教他斜竿对两角。
笨伯依言试一试,不多不少刚抵足。
借问竿长多少数,谁人算出我佩服。
旨在考查学生对勾股定理的熟练应用,并培养学生学会“说理”。
四、教学设计说明:
本教学设计对教科书“探究3”作了特殊的处理,从欣赏“自然界的海螺”过渡到“数学海螺”,激发了学生的学习兴趣,探求新知的欲望,收到了意想不到的效果,又以问题串的形式组织学生开展活动,完成了将“构造直角三角形画线段”的知识迁移到“如何在数轴上画出表示无理数的点的过程”,这种设计符合新课程改革所倡导的新课程教材观。为了使学生进一步体验勾股定理的应用价值,又提供了一个生动有趣的“蚂蚁觅食问题”,它不仅是勾股定理的应用,而且体现了二三维图形的转化,对发展学生的空间观念也有好处,教学中以恰当的情景作衬托,让“两点之间线段最短”在学生脑海中再现,蚂蚁从A点爬到B点的问题看似一个曲面上的路线问题,而实际上可以通过圆柱的侧面展开图转化为平面上的路线问题,课堂上充分发挥学生动手操作的能力,讨论交流能力和空间想象能力,让学生充分体验数学思考的魅力和知识创新的乐趣,突现敎学过程中师生互动,使学生真正成为主动学习者。正因为如此,学生对最短路程的讨论异常热烈,可以说超越了教材的讨论范围,学生综合应用三角形的不等关系和勾股定理,以及圆柱体的平面展开图特点,最终找到了解决问题的方法,并灵活的运用到实际问题的解决中。
五、说板书设计:
18.1勾股定理(四)
在数轴上表示的点,分一下四步完成:
a将在数轴上画出表示的点的问题转化为画出长为的线段的问题。
b由长为的线段是直角边都为1的直角三角形的斜边,联想到长为的线段能否是直角边为正整数的直角三角形的斜边。
c通过尝试发现,长为的线段是直角边为2,3 的直角三角形的斜边。
d画出长为的线段,从而在数轴上画出表示的点。
(设计意图:知识内容简洁清晰,重点突出,使本节内容一目了然,便于学生理解)
最后,请允许我以几句在课改中感受颇深的话语来作为我今天的结束语:
教育是探索和启蒙, 而不是宣传和灌输;
教育是平等对话和自由交流, 而不是指示和命令;
教育是丰富认识, 而不是统一思想;
教育是信任, 而不是防范。
说课稿
教 材: 人教版新教材八年级(下)
课 题: §18.1勾股定理(4)
教 师: 李 珍
朝 邑 镇 初 级 中 学
Chao yi Zhen Chu Ji Zhong Xue
二OO九年三月
“勾股定理的应用”说课稿
朝邑初中 李珍
1、 说教材分析:
本课时是人教版八年级(下)数学第十八章勾股定理第一节第四课时内容,是在掌握勾股定理的基础上对勾股定理的应用之一。
勾股定理是我国传统数学中的一大法宝。在我国几何体系中占有十分独特的地位。而且它也是中国两千多年来数学发展的一个重要的生长点。中国数学中的精髓,他为我们提供了直角三角形的三边的数量关系,既是直角三角形性质的拓展,又是后续学习解直角三角形的基础,他紧密联系了数学中最基本的两个量——数和形,能够把形(直角三角形中一个角是直角)转化成数量关系(三边之间满足),既是数形结合的典范,又体现了转化和方程思想。这些成果广泛应用于数学和实际生活的各个方面,教材在编写时注意培养学生的动手操作能力和分析能力,使学生获得较为直观的印象,通过联系和比较,了解勾股定理在实际生活的广泛应用。
(一)知识与技能目标:
1、运用勾股定理,能在数轴上找到表示无理数的点,进一步领会数形结合的思想。
2、进一步学习将实际问题转化为直角三角形的数学模型,并能用勾股定理解决简单的实际问题。
3、体验数学学习的乐趣,形成积极参与数学活动的意识,再一次感受勾股定理的应用价值。
旨在培养学生探究、创造、实践的能力。
(二)过程与方法目标;
1、经历在数轴上寻找表示无理数的点的过程中,发展学生灵活运用勾股定理解决实际问题的能力。
2、在运用勾股定理解决实际问题的过程中,体验解决问题的策略,发展学生的动手操作能力和创新精神。
3、在解决实际问题的过程中,学会与人合作,并能与他人交流思维过程和结果,形成反思的意识。
旨在培养学生数形结合能力动手操作能力和创新精神。
(三)情感目标:
1、在数轴上寻找表示无理数的点的过程中,体验勾股定理的重要作用,使他们获得成功的体验,锻炼克服困难的意志,建立自信心。
2、在解决实际问题的过程中,形成实事求是的态度以及进行质疑和独立思考的习惯。
旨在让学生体会勾股定理在生活中的广泛应用;体验数学学习的乐趣,提高应用数学的意识。
(四)教学重点难点:
1、重点:在数轴上寻找表示、、------这样的表示无理数的点。
2、难点:利用勾股定理寻找直角三角形中长度为无理数的线段。
3、教学关键:在现实情境中捕抓直角三角形,确定好直角三角形之后,再应用勾股定理。
(五)教学设备或教辅工具:
长方形图画纸一张、剪刀、画图工具、多媒体课件等。
二、说教法、学法:
(一) 教法:
“教必有法,而教无定法”,只有方法恰当,教学才会有效。根据本课内容特点和八年级学生思维活动特点,我采用了引导发现法,自主学习法。
在教学设计过程中力求让学生参与知识的发现过程,体现以学生为主体,以促进学生发展为本的教学理念,变教师知识的传授者的身份为学生自主探求知识的引导者、指导者、合作者。在学生课下收集了资料后,课上给予学生足够的时间展示、互相讲解,并鼓励学生加入自己的想法,提出独特、创新的方法在数轴上找到无理数,从而锻炼学生的思维、激发学生的创造性,优化课堂教学,努力做到由传统的数学课堂向实验课堂转变,使学生真正成为学习的主人。基于以上设计,预期本节课能收到良好的教学效果。
(二)学法:
学生都渴望与他人交流,合作探究可使学生感受到合作的重要和团队的精神力量,增强集体意识,所以本课采用小组合作的学习方式,让学生遵循“观察——猜想——验证——归纳——反馈——实践”的主线进行学习。
三、说教学程序:
本节内容的教学主要体现在学生的动手,动脑方面,根据学生的认知规律和学习心理,教学程序设置如下:
(一)创设情景,提出问题
投影出示:一张美丽的海螺图案:
设问1:同学们,你们知道吗?在数学中也有这样一幅美丽的“螺形”图案呢!学生欣赏“数学海螺(螺形图)”
设计说明:动态的多媒体课件突出了“形”的相似之处,激发学生强烈的探究欲望。
设问2.:他是怎样画出来的?是依据什么数学知识来画的?与同伴交流你的看法。
设计说明:引导学生主动探究,培养与人合作交流的能力。
(二)探索分析,解决问题:
通过观察讨论发现:
画图的依据:勾股定理。
画图的方法:先构造出长为1的等腰直角三角形,并以前一个三角形的斜边和长度为1的线段为直角边向外画直角三角形,这样就可以依次画出长度为(n是正整数)的线段。
设计说明:培养学生有条理的表达的能力。
设问3:如果我们将最初的等腰直角三角形画在数轴上(以数轴的单位1为直角边长),你能有什么新的发现?
设计说明:知识的迁移在不知不觉中完成。
设问4:你能找到,,,------,在数轴上的简便画法吗?
学生小组讨论,发现:
,,,,------,可以构造直角三角形来画图。(教师板演在数轴上画出相应的点的画图过程)
设计说明:规范画图语言和作图方法。
(三)巩固新知,反馈调控
画一画:课本第69页练习第1题。
(四)深入探究,提出问题
问题:有一个圆柱,高12cm,底面半径3cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的C点处的食物,沿圆柱侧面爬行的最短路程是多少?(π的值取3)①学生取出自制圆柱,,尝试从A点到C点沿圆柱侧面画出几条路线.思考:那条路线最短 ②如图,将圆柱侧面剪开展成一个长方形,从A点到C点的最短路线是什么 你画得对吗 ③蚂蚁从A点出发,想吃到C点处的食物,它沿圆柱侧面爬行的最短路线是什么
设计说明:趣题设置,激发兴趣。
(五)小结:
你对本节内容有哪些认识?会利用勾股定理得到一些无理数并理解数轴上的点与实数一一对应。
设计说明:这种形式的小结,激发了学生主动参与意识,调动了学生的学习兴趣,为每一位学生都创造了在数学学习活动中获得成功的体验机会,尊重学生的个体差异,满足学生多样化的学习需要,从而使小结活动不流于形式而具有时效性,为学生提供了更好的学习空间以梳理自己在本节课中的收获。
(六)作业设计:
1.必做题:A课本70页习题18.1第6 第12题;课本81页复习题18第7第8题。
B请你举一个生活中的实例,并利用勾股定理解决它。
旨在突破本节课的教学难点,通过教师的指导、学生间的合作互助,使所有的学生都获得问题的解决;
2.选做题:课本第71页习题18.1第11题。
旨在调动学生进一步参与教学活动的积极性;
3.备选题:古算趣题:“执竿进屋”
笨人执竿要进屋,无奈门框拦住竹。
横多四尺竖多二,没法急的放声哭。
有个邻居聪明着,教他斜竿对两角。
笨伯依言试一试,不多不少刚抵足。
借问竿长多少数,谁人算出我佩服。
旨在考查学生对勾股定理的熟练应用,并培养学生学会“说理”。
四、教学设计说明:
本教学设计对教科书“探究3”作了特殊的处理,从欣赏“自然界的海螺”过渡到“数学海螺”,激发了学生的学习兴趣,探求新知的欲望,收到了意想不到的效果,又以问题串的形式组织学生开展活动,完成了将“构造直角三角形画线段”的知识迁移到“如何在数轴上画出表示无理数的点的过程”,这种设计符合新课程改革所倡导的新课程教材观。为了使学生进一步体验勾股定理的应用价值,又提供了一个生动有趣的“蚂蚁觅食问题”,它不仅是勾股定理的应用,而且体现了二三维图形的转化,对发展学生的空间观念也有好处,教学中以恰当的情景作衬托,让“两点之间线段最短”在学生脑海中再现,蚂蚁从A点爬到B点的问题看似一个曲面上的路线问题,而实际上可以通过圆柱的侧面展开图转化为平面上的路线问题,课堂上充分发挥学生动手操作的能力,讨论交流能力和空间想象能力,让学生充分体验数学思考的魅力和知识创新的乐趣,突现敎学过程中师生互动,使学生真正成为主动学习者。正因为如此,学生对最短路程的讨论异常热烈,可以说超越了教材的讨论范围,学生综合应用三角形的不等关系和勾股定理,以及圆柱体的平面展开图特点,最终找到了解决问题的方法,并灵活的运用到实际问题的解决中。
五、说板书设计:
18.1勾股定理(四)
在数轴上表示的点,分一下四步完成:
a将在数轴上画出表示的点的问题转化为画出长为的线段的问题。
b由长为的线段是直角边都为1的直角三角形的斜边,联想到长为的线段能否是直角边为正整数的直角三角形的斜边。
c通过尝试发现,长为的线段是直角边为2,3 的直角三角形的斜边。
d画出长为的线段,从而在数轴上画出表示的点。
(设计意图:知识内容简洁清晰,重点突出,使本节内容一目了然,便于学生理解)
最后,请允许我以几句在课改中感受颇深的话语来作为我今天的结束语:
教育是探索和启蒙, 而不是宣传和灌输;
教育是平等对话和自由交流, 而不是指示和命令;
教育是丰富认识, 而不是统一思想;
教育是信任, 而不是防范。
