(典型易错题)1.1面的旋转解决问题 -2023-2024学年六年级下册数学高频易错尖子生培优(北师大版)(含解析)
文档属性
| 名称 | (典型易错题)1.1面的旋转解决问题 -2023-2024学年六年级下册数学高频易错尖子生培优(北师大版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览



文档简介
1.1面的旋转
1.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
2.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
3.小明给奶奶买了一个蛋糕(如图),捆扎这个蛋糕盒所用的彩带至少多少厘米?(打结部分的长度为80cm)
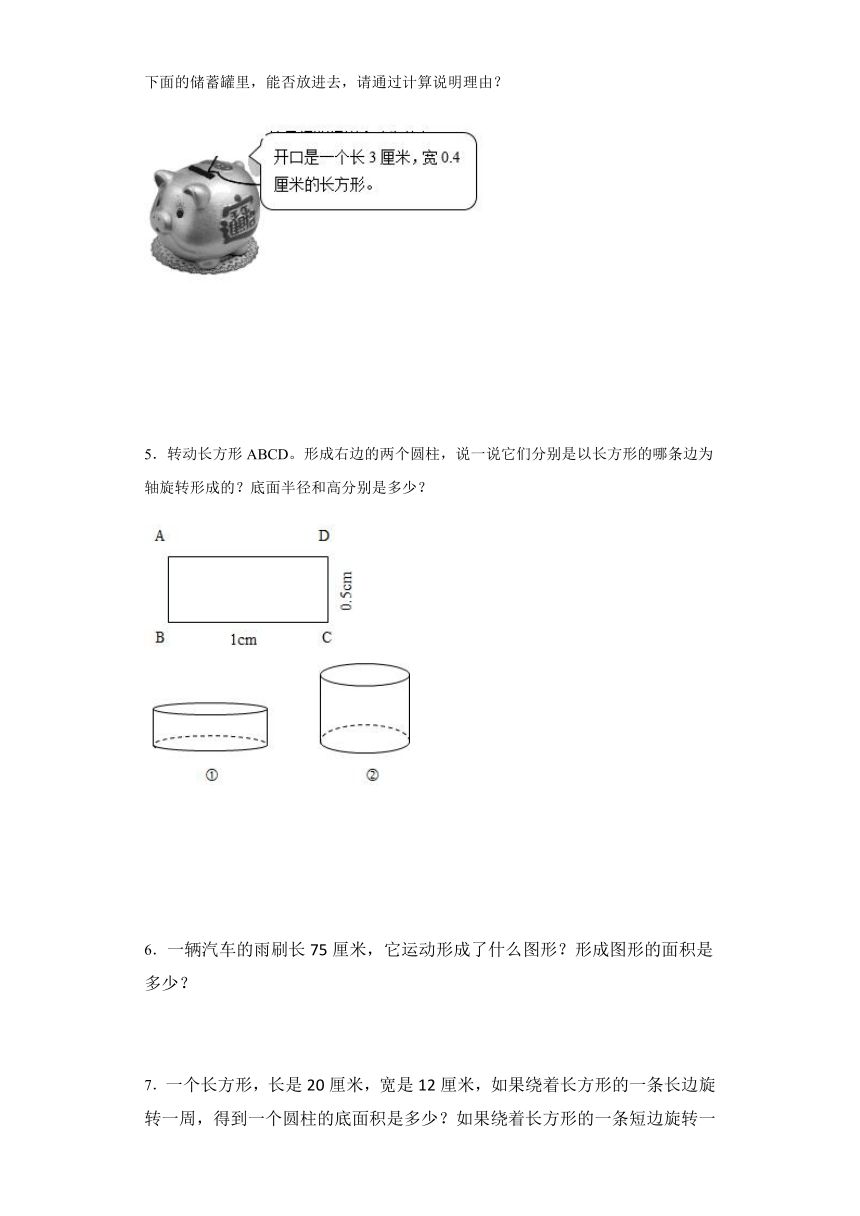
4.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
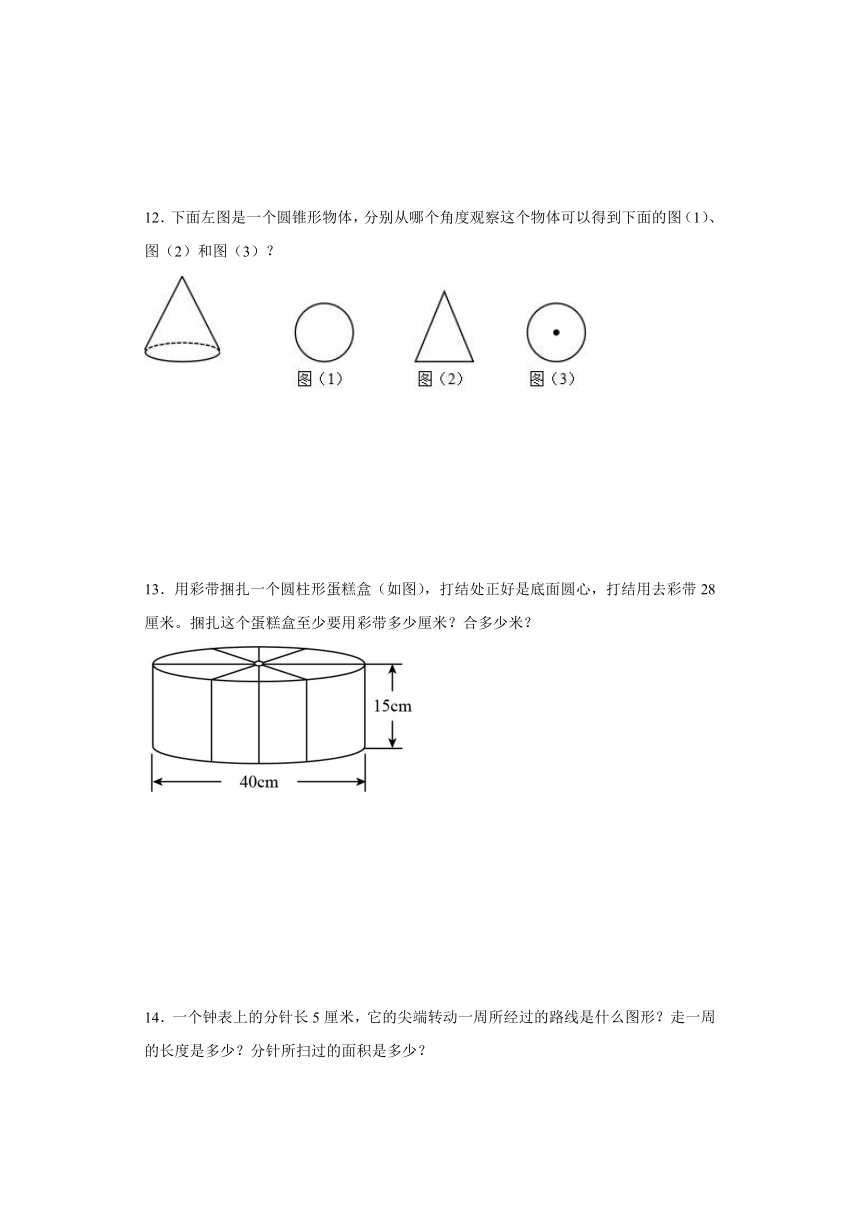
5.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
6.一辆汽车的雨刷长75厘米,它运动形成了什么图形?形成图形的面积是多少?
7.一个长方形,长是20厘米,宽是12厘米,如果绕着长方形的一条长边旋转一周,得到一个圆柱的底面积是多少?如果绕着长方形的一条短边旋转一周,得到圆柱的底面积又是多少?
8.把一个直径为20分米的圆形铁皮剪下一半围成一个圆锥,该圆锥的用铁皮多少平方分米?该圆锥的底面圆半径是多少分米?(接头不计,π取两位小数)
9.某种啤酒的包装是圆柱体,底面半径为8厘米,高为12厘米,将24罐放在箱子里,放3排,每排4罐,上下两层刚好合适,这个箱子的长、宽、高至少是多少?
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
11.有一个圆柱形的面包,要切一刀把它变成两块,截面会是什么形状的图形?(沿平行于底面和垂直于底面两个方向切)
12.下面左图是一个圆锥形物体,分别从哪个角度观察这个物体可以得到下面的图(1)、图(2)和图(3)?
13.用彩带捆扎一个圆柱形蛋糕盒(如图),打结处正好是底面圆心,打结用去彩带28厘米。捆扎这个蛋糕盒至少要用彩带多少厘米?合多少米?
14.一个钟表上的分针长5厘米,它的尖端转动一周所经过的路线是什么图形?走一周的长度是多少?分针所扫过的面积是多少?
15.某公路有一段路需要维修,工人摆了一些路障,每个圆锥底面直径为50厘米,一共摆了15个,每两个圆锥间的距离是1.5米,从第一个圆锥到最后一个圆锥共占多长的路面?
16.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
17.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
18.(如下图)妈妈给小明买了一个生日蛋糕,蛋糕盒上扎了一条漂亮的丝带.捆扎方法如图,已知蛋糕盒底面直径是30cm,高是16cm,打结部分长28cm,这条丝带至少长多少cm?
19.用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳子12厘米。扎这个盒子至少用塑料绳多少厘米?
20.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
参考答案:
1.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
2.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点睛】本题考查了圆柱的特征,用圆柱的底面周长÷π=底面直径。
3.340厘米
【分析】蛋糕是十字形捆扎,所以捆扎的丝带包括4个直径,4条高和打结的部分.把这三部分合起来就是困蛋糕绳子的长度.
【详解】40×4+25×4+80=340(cm)
答:捆扎这个蛋糕盒所用的彩带至少340厘米.
4.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
【点睛】本题主要考查圆柱的特征,注意圆柱的直径与厚度有一项大于开口处就不能放进去。
5.见详解
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
【点睛】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
6.半圆形 752×3.14÷2=8831.25(平方厘米) 答:形成图形的面积是8831.25平方厘米.
【详解】把汽车的雨刷看成一条线段,它的运动形成的是一个面,根据实际情况可知,它的运动形成的是一个半圆形,故要计算半径是75厘米的半圆形的面积.
7.3.14×122=452.16(平方厘米) 3.14×202=1256(平方厘米)
答:如果绕着长方形的一条长边旋转一周,得到圆柱的底面积是452.16平方厘米.如果绕着长方形的一条短边旋转一周,得到圆柱的底面积是1256平方厘米.
【详解】通过旋转、观察可知,如果绕着长方形的一条长边旋转一周,则长方形的长旋转后是圆柱的高,长方形的宽旋转后是圆柱的底面半径.故要求圆柱的底面积就是求以12厘米为半径的圆的面积;如果绕着长方形的一条短边旋转一周,则长方形的宽旋转后是圆柱的高,长方形的长旋转后是圆柱的底面半径.故要求圆柱的底面积就是求以20厘米为半径的圆的面积.
8.15.7平方分米;62.8分米
【分析】通过分析,先求得半圆面积,就是圆锥侧面积;根据圆周长的一半为圆锥底面圆的周长再求圆锥底面圆的半径.
【详解】() π÷2=15.7(平方分米) 20π÷2÷2π=5(分米)
答:用铁皮15.7平方分米;底面圆半径是5分米.
9.长:8×2×4=64(厘米) 宽:8×2×3=48(厘米) 高:12×2=24(厘米)
答:箱子的长至少是64厘米,宽至少是48厘米,高至少是24厘米.
【详解】由题意可知,箱子的长是4个圆柱的底面直径,箱子的宽是3个圆柱的底面直径,箱子的高是2个圆柱的高,并且圆柱的底面半径和高也是已知的.
10.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
11.把圆柱形面包平行于底面切割,切面是和底面大小相同的两个圆;把圆柱形面包垂直于底面切割,切面是两个完全相同的长方形(或正方形),且沿底面直径切割是最大的长方形(或正方形).
【详解】略
12.从底面观察,可以得到图(1);
从正面或侧面观察,可以得到图(2);
从上面观察,可以得到图(3)。
【详解】一个圆锥,从上面看是一个圆形,可以看到圆心,从侧面或是正面看到的是一个三角形,从底面看是一个圆形,看不到圆心。
13.468厘米;4.68米
【分析】由图可知:所用彩带的长=圆柱直径×8+高×8+打结处的长度,代入数据计算即可。
【详解】40×8+15×8+28
=320+120+28
=468(厘米)
468厘米=4.68米
答:捆扎这个蛋糕盒至少要用彩带468厘米,合4.68米。
【点睛】本题主要考查圆柱的特征,明确有几条直径、几条高是解题的关键。
14.圆形 5×2×3.14=31.4(厘米) 52×3.14=78.5(平方厘米) 答:走一周的长度是31.4厘米,分针所扫过的面积是78.5平方厘米.
【详解】把分针的尖端看成一个点,它转动一周形成一个圆形曲线;把分针看成一条线段,它转动一周形成一个圆形平面.且分针的长5厘米是形成圆的半径.即分针尖端走一周的长度是圆形的周长,分针扫过的面积是圆形的面积.
15.50厘米=0.5米 0.5×15+1.5×14=28.5(米) 答:共占28.5米长的路面.
【详解】由题意可知,从第一个圆锥到最后一个圆锥的距离由15个圆锥底面直径和14个“每两个圆锥间的距离”组成,另外要注意先统一单位再计算.
16.圆,长方形(或正方形)。
.
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
17.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
【点睛】本题主要考查圆柱的特征,圆柱是由两个底面和一个侧面构成,两个底面是大小相等的圆。
18.304cm
【分析】与高相等的有6条,与底面直径相等的有6条,再加上打结部分的长度就是丝带的总长度.
【详解】16×6+30×6+28
=96+180+28
=304(cm)
答:这条丝带至少长304cm.
19.252厘米
【分析】由图可知:塑料绳的长度等于4条直径+4条高+打结用去的长度;据此解答。
【详解】40×4+20×4+12
=160+80+12
=252(厘米)
答:扎这个盒子至少用塑料绳252厘米。
【点睛】本题主要考查圆柱的特征,明确有几条直径、几条高是解题的关键。
20.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm。
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56cm,即可解答。
【详解】(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律。
1.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
2.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
3.小明给奶奶买了一个蛋糕(如图),捆扎这个蛋糕盒所用的彩带至少多少厘米?(打结部分的长度为80cm)
4.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
5.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
6.一辆汽车的雨刷长75厘米,它运动形成了什么图形?形成图形的面积是多少?
7.一个长方形,长是20厘米,宽是12厘米,如果绕着长方形的一条长边旋转一周,得到一个圆柱的底面积是多少?如果绕着长方形的一条短边旋转一周,得到圆柱的底面积又是多少?
8.把一个直径为20分米的圆形铁皮剪下一半围成一个圆锥,该圆锥的用铁皮多少平方分米?该圆锥的底面圆半径是多少分米?(接头不计,π取两位小数)
9.某种啤酒的包装是圆柱体,底面半径为8厘米,高为12厘米,将24罐放在箱子里,放3排,每排4罐,上下两层刚好合适,这个箱子的长、宽、高至少是多少?
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
11.有一个圆柱形的面包,要切一刀把它变成两块,截面会是什么形状的图形?(沿平行于底面和垂直于底面两个方向切)
12.下面左图是一个圆锥形物体,分别从哪个角度观察这个物体可以得到下面的图(1)、图(2)和图(3)?
13.用彩带捆扎一个圆柱形蛋糕盒(如图),打结处正好是底面圆心,打结用去彩带28厘米。捆扎这个蛋糕盒至少要用彩带多少厘米?合多少米?
14.一个钟表上的分针长5厘米,它的尖端转动一周所经过的路线是什么图形?走一周的长度是多少?分针所扫过的面积是多少?
15.某公路有一段路需要维修,工人摆了一些路障,每个圆锥底面直径为50厘米,一共摆了15个,每两个圆锥间的距离是1.5米,从第一个圆锥到最后一个圆锥共占多长的路面?
16.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
17.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
18.(如下图)妈妈给小明买了一个生日蛋糕,蛋糕盒上扎了一条漂亮的丝带.捆扎方法如图,已知蛋糕盒底面直径是30cm,高是16cm,打结部分长28cm,这条丝带至少长多少cm?
19.用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳子12厘米。扎这个盒子至少用塑料绳多少厘米?
20.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
参考答案:
1.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
2.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点睛】本题考查了圆柱的特征,用圆柱的底面周长÷π=底面直径。
3.340厘米
【分析】蛋糕是十字形捆扎,所以捆扎的丝带包括4个直径,4条高和打结的部分.把这三部分合起来就是困蛋糕绳子的长度.
【详解】40×4+25×4+80=340(cm)
答:捆扎这个蛋糕盒所用的彩带至少340厘米.
4.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
【点睛】本题主要考查圆柱的特征,注意圆柱的直径与厚度有一项大于开口处就不能放进去。
5.见详解
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
【点睛】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
6.半圆形 752×3.14÷2=8831.25(平方厘米) 答:形成图形的面积是8831.25平方厘米.
【详解】把汽车的雨刷看成一条线段,它的运动形成的是一个面,根据实际情况可知,它的运动形成的是一个半圆形,故要计算半径是75厘米的半圆形的面积.
7.3.14×122=452.16(平方厘米) 3.14×202=1256(平方厘米)
答:如果绕着长方形的一条长边旋转一周,得到圆柱的底面积是452.16平方厘米.如果绕着长方形的一条短边旋转一周,得到圆柱的底面积是1256平方厘米.
【详解】通过旋转、观察可知,如果绕着长方形的一条长边旋转一周,则长方形的长旋转后是圆柱的高,长方形的宽旋转后是圆柱的底面半径.故要求圆柱的底面积就是求以12厘米为半径的圆的面积;如果绕着长方形的一条短边旋转一周,则长方形的宽旋转后是圆柱的高,长方形的长旋转后是圆柱的底面半径.故要求圆柱的底面积就是求以20厘米为半径的圆的面积.
8.15.7平方分米;62.8分米
【分析】通过分析,先求得半圆面积,就是圆锥侧面积;根据圆周长的一半为圆锥底面圆的周长再求圆锥底面圆的半径.
【详解】() π÷2=15.7(平方分米) 20π÷2÷2π=5(分米)
答:用铁皮15.7平方分米;底面圆半径是5分米.
9.长:8×2×4=64(厘米) 宽:8×2×3=48(厘米) 高:12×2=24(厘米)
答:箱子的长至少是64厘米,宽至少是48厘米,高至少是24厘米.
【详解】由题意可知,箱子的长是4个圆柱的底面直径,箱子的宽是3个圆柱的底面直径,箱子的高是2个圆柱的高,并且圆柱的底面半径和高也是已知的.
10.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
11.把圆柱形面包平行于底面切割,切面是和底面大小相同的两个圆;把圆柱形面包垂直于底面切割,切面是两个完全相同的长方形(或正方形),且沿底面直径切割是最大的长方形(或正方形).
【详解】略
12.从底面观察,可以得到图(1);
从正面或侧面观察,可以得到图(2);
从上面观察,可以得到图(3)。
【详解】一个圆锥,从上面看是一个圆形,可以看到圆心,从侧面或是正面看到的是一个三角形,从底面看是一个圆形,看不到圆心。
13.468厘米;4.68米
【分析】由图可知:所用彩带的长=圆柱直径×8+高×8+打结处的长度,代入数据计算即可。
【详解】40×8+15×8+28
=320+120+28
=468(厘米)
468厘米=4.68米
答:捆扎这个蛋糕盒至少要用彩带468厘米,合4.68米。
【点睛】本题主要考查圆柱的特征,明确有几条直径、几条高是解题的关键。
14.圆形 5×2×3.14=31.4(厘米) 52×3.14=78.5(平方厘米) 答:走一周的长度是31.4厘米,分针所扫过的面积是78.5平方厘米.
【详解】把分针的尖端看成一个点,它转动一周形成一个圆形曲线;把分针看成一条线段,它转动一周形成一个圆形平面.且分针的长5厘米是形成圆的半径.即分针尖端走一周的长度是圆形的周长,分针扫过的面积是圆形的面积.
15.50厘米=0.5米 0.5×15+1.5×14=28.5(米) 答:共占28.5米长的路面.
【详解】由题意可知,从第一个圆锥到最后一个圆锥的距离由15个圆锥底面直径和14个“每两个圆锥间的距离”组成,另外要注意先统一单位再计算.
16.圆,长方形(或正方形)。
.
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
17.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
【点睛】本题主要考查圆柱的特征,圆柱是由两个底面和一个侧面构成,两个底面是大小相等的圆。
18.304cm
【分析】与高相等的有6条,与底面直径相等的有6条,再加上打结部分的长度就是丝带的总长度.
【详解】16×6+30×6+28
=96+180+28
=304(cm)
答:这条丝带至少长304cm.
19.252厘米
【分析】由图可知:塑料绳的长度等于4条直径+4条高+打结用去的长度;据此解答。
【详解】40×4+20×4+12
=160+80+12
=252(厘米)
答:扎这个盒子至少用塑料绳252厘米。
【点睛】本题主要考查圆柱的特征,明确有几条直径、几条高是解题的关键。
20.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm。
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56cm,即可解答。
【详解】(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律。
