27.1 图形的相似 课件(共26张PPT)
文档属性
| 名称 | 27.1 图形的相似 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 18:38:42 | ||
图片预览






文档简介
(共26张PPT)
人教版数学九年级下册
第二十七章 相 似
27.1 图形的相似
(第1课时)
欣赏图片
(1)大小不同的汽车照片
(2)大小不同的两个足球
上面各组图片的共同之处是什么
(3)大小不同的两张照片
学 习 新 知
问题思考
认识相似图形
【思考1】 以上展示的图片之间有什么特点 它们的形状和大小有怎样的关系
它们形状相同、大小不等.
形状相同的图形叫做相似图形.
【思考2】全等形一定是相似图形吗 相似图形一定全等吗 它们之间有什么关系
全等图形是相似图形的一种特殊情况.全等图形一定相似,相似图形不一定全等.
【思考3】 你能举出现实生活中一些相似图形的例子吗
相似图形的特征
观察下列每组图形,是不是相似图形
(5)相似图形是否可以看作其中一个图形是由另一个图形放大或缩小得到的
【思考】
(1)两个相似的平面图形之间有什么关系
(2)两个相似图形的主要特征是什么
(3)如何判定两个图形是相似图形
(4)相似图形的大小是不是一定相等
【结论】相似图形的特征是:形状相同.两个图形的形状相同,则两个图形就是相似图形.相似图形的大小不一定相等,其中一个图形可以看作是由另一个图形放大或缩小得到的.
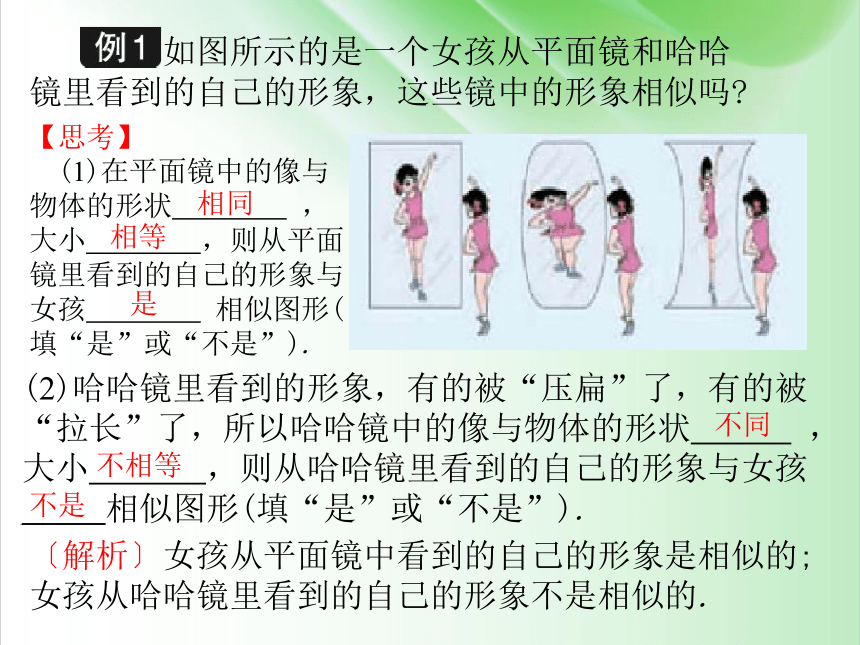
如图所示的是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗
【思考】
(1)在平面镜中的像与物体的形状 ,大小 ,则从平面镜里看到的自己的形象与女孩 相似图形(填“是”或“不是”).
(2)哈哈镜里看到的形象,有的被“压扁”了,有的被“拉长”了,所以哈哈镜中的像与物体的形状 ,大小 ,则从哈哈镜里看到的自己的形象与女孩 _____相似图形(填“是”或“不是”).
〔解析〕女孩从平面镜中看到的自己的形象是相似的;女孩从哈哈镜里看到的自己的形象不是相似的.
相同
相等
是
不同
不相等
不是
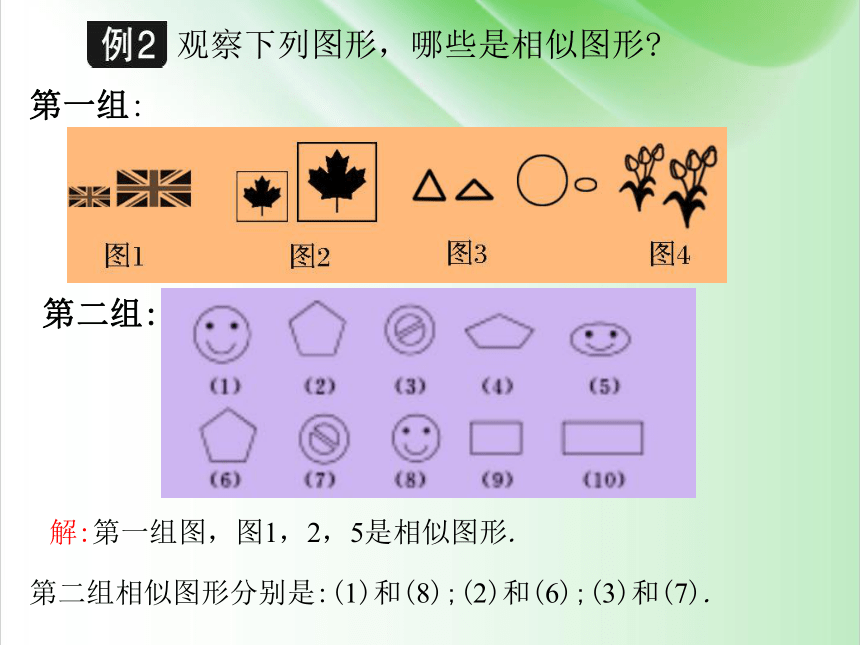
观察下列图形,哪些是相似图形
第一组:
第二组:
第二组相似图形分别是:(1)和(8);(2)和(6);(3)和(7).
解:第一组图,图1,2,5是相似图形.
【知识拓展】所谓“形状相同”,就是与图形的大小、位置无关,与摆放角度、摆放方向也无关.有些图形之间虽然只有很小的形状差异,但也不能认为是“形状相同”.
【课堂小结】
1.相似图形定义:形状相同的图形叫做相似图形.
2.相似图形与全等形之间的关系.
3.相似图形的特征:形状相同.
检测反馈
1.下列四个命题:①所有的直角三角形都相似;②所有的等腰三角形都相似;③所有的正方形都相似;④所有的菱形都相似.其中正确的有 ( )
A.2个 B.3个 C.4个 D.1个
解析:所有的正方形的形状相同,所以③正确;直角三角形、等腰三角形、菱形的形状和内角有关,角度不同,图形的形状就不同,所以所有的直角三角形、所有的等腰三角形、所有的菱形不一定相似.故选D.
D
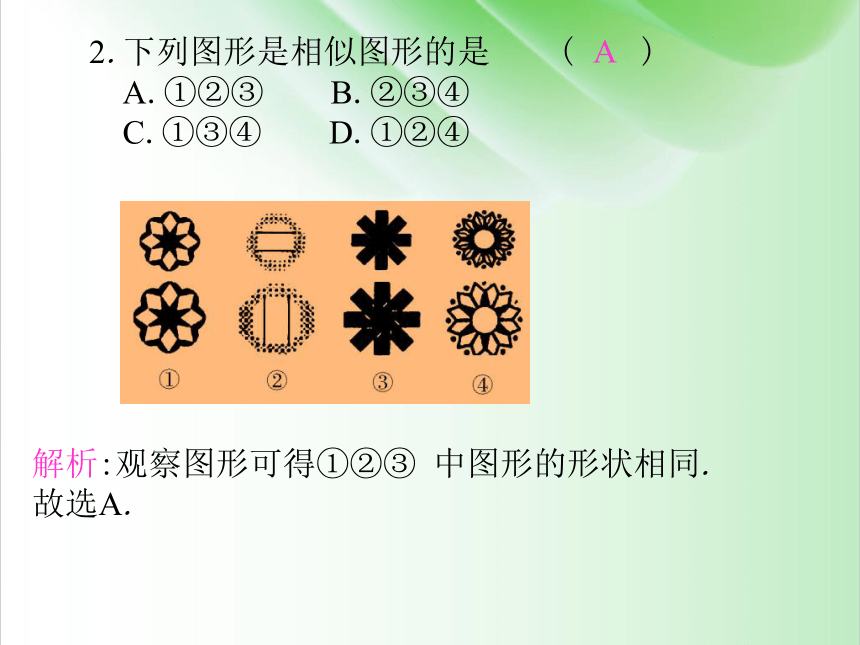
2.下列图形是相似图形的是 ( )
A.①②③ B.②③④
C.①③④ D.①②④
解析:观察图形可得①②③ 中图形的形状相同.故选A.
A
3.下列图形不是相似图形的是 ( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
解析:某人的侧面照片和正面照片形状不相同,不是相似图形.故选C.
C
4.如图所示,用放大镜将图形放大,应该属于 ( )
A.相似变换
B.平移变换
C.对称变换
D.旋转变换
解析:相似图形的形状相同,其中一个图形可以看作是由另一个图形放大或缩小得到的.所以用放大镜放大图形属于相似变换.故选A.
A
人教版数学九年级下册
第二十七章 相 似
27.1 图形的相似
(第2课时)
学 习 新 知
问题思考
如图所示的一块黑板,长3米,宽1.5米,加一7.5厘米宽的边框,边框外围与边框里边的矩形形状相同吗
成比例线段概念
(1)把九年级数学课本的两个邻边看作两条线段AB和CD,那么什么是这两条线段的比
(这两条线段的长度比叫做这两条线段的比)
(2)对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等, (即ad=bc),我们就说这四条线段成比例.
(3)如何判断四条线段是成比例线段
(四条线段中其中两条线段的比与另两条线段的比相等,就说这四条线段成比例)
(成比例线段概念中的四条线段是有顺序的,如a,b,c,d是成比例线段与a,d,b,c是成比例线段得到的比例式是不同的)
(4)成比例线段的概念中应注意什么问题
认识相似多边形
如图所示,将△ABC用2倍放大镜观察得到△A1B1C1,这两个三角形相似吗
(1)问题思考.
①△ABC及用2倍放大镜观察得到的△A1B1C1中,对应角之间的数量关系为:∠A ∠A1,∠B ∠B1,∠C ∠C1;
②四边形ABCD及用2倍放大镜观察得到的四边形A1B1C1D1中,对应角之间的数量关系为:∠A ∠A1,∠B ∠B1,∠C ∠C1,∠D ∠D1;
③放大镜下的图形与原图形是否相似 两个图形的对应角、对应边之间有什么关系
(相似,对应角相等,对应边成比例)
④你能尝试给出相似多边形的定义吗 并尝试用几何语言表示出来.
⑤相似比的值与两个相似多边形的顺序有关吗
⑥相似多边形的对应角、对应边有什么特点 用几何语言怎样表示
相似多边形定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
【几何语言】 如图所示的两个大小不同的四边形ABCD和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1; 因此四边形ABCD与四边形A1B1C1D1相似.
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
如上图,∵四边形ABCD与四边形A1B1C1D1相似,∴ ∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
判断正误,正确的说明理由,错误的举出反例.
(1)所有的矩形都相似. ( )
(2)所有的菱形都相似. ( )
(3)所有的正方形都相似. ( )
(4)所有的等腰直角三角形都相似. ( )
(5)所有的等边三角形都相似. ( )
正
误
误
误
正
(教材例题)如图所示,四边形ABCD与EFGH相似,求角α,β 的大小和EH的长度x.
【思考】
(1)相似多边形的性质是什么
(2)根据相似多边形的性质,你能求出∠F,∠G的大小吗
(3)四边形的内角和是多少度
(4)由四边形内角和定理,能否求出∠H的值
(5)相似四边形中,对应边AB与EF,AD与EH之间有什么关系
(6)在比例式中,已知三条线段的长能否求出第四条线段的长 尝试求出EH的值.
解:∵四边形ABCD与四边形EFGH相似,
∴α=∠C=83°,∠A=∠E=118°, ,
即 解得x=28.
在四边形ABCD中, β=360°-83°-78°-118°=81°.
[知识拓展]
(1)式子 也可以写成a∶b=c∶d,通常这里的a叫做第一比例项,b叫做第二比例项,c叫做第三比例项,d叫做第四比例项.
(2)有时在 中,b=c,例如= ,这时我们把b(或c)叫做a,d的比例中项,此时b2(或c2)=ad.
(3)在式子 的两边同时乘bd,得ad=cb,在与比例有关的计算中,我们常通过上述变形转化字母之间的关系.
(4)通常情况下,四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b和c,d的单位分别一致也可以.
(5)在相似多边形中,“对应边成比例”“对应角相等”这两个条件必须同时成立时,才能说明这两个多边形是相似多边形.
(6)相似多边形的性质可以用来确定两个多边形中未知的边的长度或未知的角的度数.
(7)相似比的值与两个多边形的前后顺序有关.
(8)相似比为1∶1的两个相似多边形是全等多边形.
课堂小结
3.相似多边形的性质:相似多边形的对应角相等,对应边成比例.
1.成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
2.相似多边形的定义: 两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
检测反馈
解析:两个边数相同的多边形,满足对应边成比例、对应角相等的多边形叫做相似多边形,两个条件缺一不可,所以A,C错误,D正确;边数不相等的多边形一定不相似,所以B错误.故选D.
1.关于相似多边形的下列叙述正确的是 ( )
A.对应边相等的多边形叫做相似多边形
B.多边形的边数不同时也可以相似
C.对应角、对应边都相等的多边形叫做相似多边形
D.对应角相等、对应边成比例的多边形叫做相似多边形
D
解析:根据相似多边形对应边成比例得相似比为 ,所以边长为1,2,3,4的各边对应的边长为
则周长为 +7=21.故选C.
2.一个五边形的各边长分别为1,2,3,4,5,另一个和它相似的五边形的最长边的长为7,则后一个五边形的周长为 ( )
A.27 B.25
C.21 D.18
C
3.已知a,b,c,d是成比例线段,且a=3 cm,b=2 cm,c=6 cm,则d= cm.
解析:因为a,b,c,d是成比例线段,所以 ,把a=3 cm,b=2 cm,c=6 cm代入,得 ,解得d=4 cm.故填4.
4
4.在比例尺为1∶6000000的地图上,量得南京到北京的距离是15 cm,则这两地的实际距离是 km.
解析:设两地的实际距离为x cm.根据图上距离与实际距离的比等于比例尺,得 ,解得x=90000000,90000000 cm=900 km.故填900.
900
5.如图所示,六边形ABCDEF与六边形A'B'C'D'E'F'相似,已知AB=5 cm,EF=6 cm,CD与C'D'的比值为1∶3,∠E=125°,求A'B',E'F'的长及∠E'的度数.
解:∵六边形ABCDEF与六边形A'B'C'D'E'F'相似,
∴ ,∠E'=∠E=125°.
∴A'B'=3AB=15 cm,E'F'=3EF=18 cm.
THANK YOU
人教版数学九年级下册
第二十七章 相 似
27.1 图形的相似
(第1课时)
欣赏图片
(1)大小不同的汽车照片
(2)大小不同的两个足球
上面各组图片的共同之处是什么
(3)大小不同的两张照片
学 习 新 知
问题思考
认识相似图形
【思考1】 以上展示的图片之间有什么特点 它们的形状和大小有怎样的关系
它们形状相同、大小不等.
形状相同的图形叫做相似图形.
【思考2】全等形一定是相似图形吗 相似图形一定全等吗 它们之间有什么关系
全等图形是相似图形的一种特殊情况.全等图形一定相似,相似图形不一定全等.
【思考3】 你能举出现实生活中一些相似图形的例子吗
相似图形的特征
观察下列每组图形,是不是相似图形
(5)相似图形是否可以看作其中一个图形是由另一个图形放大或缩小得到的
【思考】
(1)两个相似的平面图形之间有什么关系
(2)两个相似图形的主要特征是什么
(3)如何判定两个图形是相似图形
(4)相似图形的大小是不是一定相等
【结论】相似图形的特征是:形状相同.两个图形的形状相同,则两个图形就是相似图形.相似图形的大小不一定相等,其中一个图形可以看作是由另一个图形放大或缩小得到的.
如图所示的是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗
【思考】
(1)在平面镜中的像与物体的形状 ,大小 ,则从平面镜里看到的自己的形象与女孩 相似图形(填“是”或“不是”).
(2)哈哈镜里看到的形象,有的被“压扁”了,有的被“拉长”了,所以哈哈镜中的像与物体的形状 ,大小 ,则从哈哈镜里看到的自己的形象与女孩 _____相似图形(填“是”或“不是”).
〔解析〕女孩从平面镜中看到的自己的形象是相似的;女孩从哈哈镜里看到的自己的形象不是相似的.
相同
相等
是
不同
不相等
不是
观察下列图形,哪些是相似图形
第一组:
第二组:
第二组相似图形分别是:(1)和(8);(2)和(6);(3)和(7).
解:第一组图,图1,2,5是相似图形.
【知识拓展】所谓“形状相同”,就是与图形的大小、位置无关,与摆放角度、摆放方向也无关.有些图形之间虽然只有很小的形状差异,但也不能认为是“形状相同”.
【课堂小结】
1.相似图形定义:形状相同的图形叫做相似图形.
2.相似图形与全等形之间的关系.
3.相似图形的特征:形状相同.
检测反馈
1.下列四个命题:①所有的直角三角形都相似;②所有的等腰三角形都相似;③所有的正方形都相似;④所有的菱形都相似.其中正确的有 ( )
A.2个 B.3个 C.4个 D.1个
解析:所有的正方形的形状相同,所以③正确;直角三角形、等腰三角形、菱形的形状和内角有关,角度不同,图形的形状就不同,所以所有的直角三角形、所有的等腰三角形、所有的菱形不一定相似.故选D.
D
2.下列图形是相似图形的是 ( )
A.①②③ B.②③④
C.①③④ D.①②④
解析:观察图形可得①②③ 中图形的形状相同.故选A.
A
3.下列图形不是相似图形的是 ( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
解析:某人的侧面照片和正面照片形状不相同,不是相似图形.故选C.
C
4.如图所示,用放大镜将图形放大,应该属于 ( )
A.相似变换
B.平移变换
C.对称变换
D.旋转变换
解析:相似图形的形状相同,其中一个图形可以看作是由另一个图形放大或缩小得到的.所以用放大镜放大图形属于相似变换.故选A.
A
人教版数学九年级下册
第二十七章 相 似
27.1 图形的相似
(第2课时)
学 习 新 知
问题思考
如图所示的一块黑板,长3米,宽1.5米,加一7.5厘米宽的边框,边框外围与边框里边的矩形形状相同吗
成比例线段概念
(1)把九年级数学课本的两个邻边看作两条线段AB和CD,那么什么是这两条线段的比
(这两条线段的长度比叫做这两条线段的比)
(2)对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等, (即ad=bc),我们就说这四条线段成比例.
(3)如何判断四条线段是成比例线段
(四条线段中其中两条线段的比与另两条线段的比相等,就说这四条线段成比例)
(成比例线段概念中的四条线段是有顺序的,如a,b,c,d是成比例线段与a,d,b,c是成比例线段得到的比例式是不同的)
(4)成比例线段的概念中应注意什么问题
认识相似多边形
如图所示,将△ABC用2倍放大镜观察得到△A1B1C1,这两个三角形相似吗
(1)问题思考.
①△ABC及用2倍放大镜观察得到的△A1B1C1中,对应角之间的数量关系为:∠A ∠A1,∠B ∠B1,∠C ∠C1;
②四边形ABCD及用2倍放大镜观察得到的四边形A1B1C1D1中,对应角之间的数量关系为:∠A ∠A1,∠B ∠B1,∠C ∠C1,∠D ∠D1;
③放大镜下的图形与原图形是否相似 两个图形的对应角、对应边之间有什么关系
(相似,对应角相等,对应边成比例)
④你能尝试给出相似多边形的定义吗 并尝试用几何语言表示出来.
⑤相似比的值与两个相似多边形的顺序有关吗
⑥相似多边形的对应角、对应边有什么特点 用几何语言怎样表示
相似多边形定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
【几何语言】 如图所示的两个大小不同的四边形ABCD和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1; 因此四边形ABCD与四边形A1B1C1D1相似.
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
如上图,∵四边形ABCD与四边形A1B1C1D1相似,∴ ∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
判断正误,正确的说明理由,错误的举出反例.
(1)所有的矩形都相似. ( )
(2)所有的菱形都相似. ( )
(3)所有的正方形都相似. ( )
(4)所有的等腰直角三角形都相似. ( )
(5)所有的等边三角形都相似. ( )
正
误
误
误
正
(教材例题)如图所示,四边形ABCD与EFGH相似,求角α,β 的大小和EH的长度x.
【思考】
(1)相似多边形的性质是什么
(2)根据相似多边形的性质,你能求出∠F,∠G的大小吗
(3)四边形的内角和是多少度
(4)由四边形内角和定理,能否求出∠H的值
(5)相似四边形中,对应边AB与EF,AD与EH之间有什么关系
(6)在比例式中,已知三条线段的长能否求出第四条线段的长 尝试求出EH的值.
解:∵四边形ABCD与四边形EFGH相似,
∴α=∠C=83°,∠A=∠E=118°, ,
即 解得x=28.
在四边形ABCD中, β=360°-83°-78°-118°=81°.
[知识拓展]
(1)式子 也可以写成a∶b=c∶d,通常这里的a叫做第一比例项,b叫做第二比例项,c叫做第三比例项,d叫做第四比例项.
(2)有时在 中,b=c,例如= ,这时我们把b(或c)叫做a,d的比例中项,此时b2(或c2)=ad.
(3)在式子 的两边同时乘bd,得ad=cb,在与比例有关的计算中,我们常通过上述变形转化字母之间的关系.
(4)通常情况下,四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b和c,d的单位分别一致也可以.
(5)在相似多边形中,“对应边成比例”“对应角相等”这两个条件必须同时成立时,才能说明这两个多边形是相似多边形.
(6)相似多边形的性质可以用来确定两个多边形中未知的边的长度或未知的角的度数.
(7)相似比的值与两个多边形的前后顺序有关.
(8)相似比为1∶1的两个相似多边形是全等多边形.
课堂小结
3.相似多边形的性质:相似多边形的对应角相等,对应边成比例.
1.成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
2.相似多边形的定义: 两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
检测反馈
解析:两个边数相同的多边形,满足对应边成比例、对应角相等的多边形叫做相似多边形,两个条件缺一不可,所以A,C错误,D正确;边数不相等的多边形一定不相似,所以B错误.故选D.
1.关于相似多边形的下列叙述正确的是 ( )
A.对应边相等的多边形叫做相似多边形
B.多边形的边数不同时也可以相似
C.对应角、对应边都相等的多边形叫做相似多边形
D.对应角相等、对应边成比例的多边形叫做相似多边形
D
解析:根据相似多边形对应边成比例得相似比为 ,所以边长为1,2,3,4的各边对应的边长为
则周长为 +7=21.故选C.
2.一个五边形的各边长分别为1,2,3,4,5,另一个和它相似的五边形的最长边的长为7,则后一个五边形的周长为 ( )
A.27 B.25
C.21 D.18
C
3.已知a,b,c,d是成比例线段,且a=3 cm,b=2 cm,c=6 cm,则d= cm.
解析:因为a,b,c,d是成比例线段,所以 ,把a=3 cm,b=2 cm,c=6 cm代入,得 ,解得d=4 cm.故填4.
4
4.在比例尺为1∶6000000的地图上,量得南京到北京的距离是15 cm,则这两地的实际距离是 km.
解析:设两地的实际距离为x cm.根据图上距离与实际距离的比等于比例尺,得 ,解得x=90000000,90000000 cm=900 km.故填900.
900
5.如图所示,六边形ABCDEF与六边形A'B'C'D'E'F'相似,已知AB=5 cm,EF=6 cm,CD与C'D'的比值为1∶3,∠E=125°,求A'B',E'F'的长及∠E'的度数.
解:∵六边形ABCDEF与六边形A'B'C'D'E'F'相似,
∴ ,∠E'=∠E=125°.
∴A'B'=3AB=15 cm,E'F'=3EF=18 cm.
THANK YOU
