2023年盐城市中考数学试卷（含解析）

2023年盐城市中考数学试卷
一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，恰有一项是符合题目要求的）
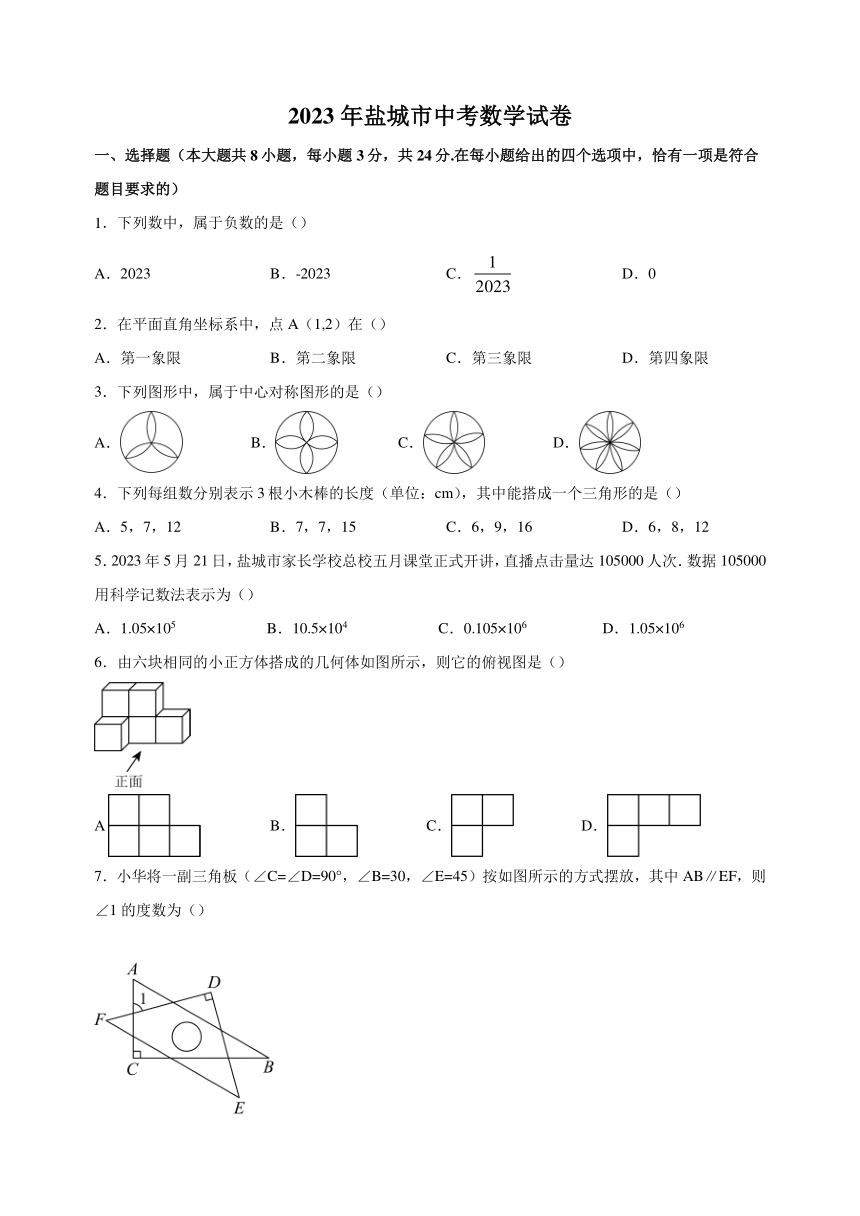
1．下列数中，属于负数的是（）
A．2023 B．-2023 C． D．0
2．在平面直角坐标系中，点A（1,2）在（）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3．下列图形中，属于中心对称图形的是（）
A． B． C． D．
4．下列每组数分别表示3根小木棒的长度（单位：cm），其中能搭成一个三角形的是（）
A．5，7，12 B．7，7，15 C．6，9，16 D．6，8，12
5．2023年5月21日，盐城市家长学校总校五月课堂正式开讲，直播点击量达105000人次．数据105000用科学记数法表示为（）
A．1.05×105 B．10.5×104 C．0.105×106 D．1.05×106
6．由六块相同的小正方体搭成的几何体如图所示，则它的俯视图是（）
A B． C． D．
7．小华将一副三角板（∠C=∠D=90°，∠B=30，∠E=45）按如图所示的方式摆放，其中AB∥EF，则∠1的度数为（）
A．45° B．60° C．75° D．105°
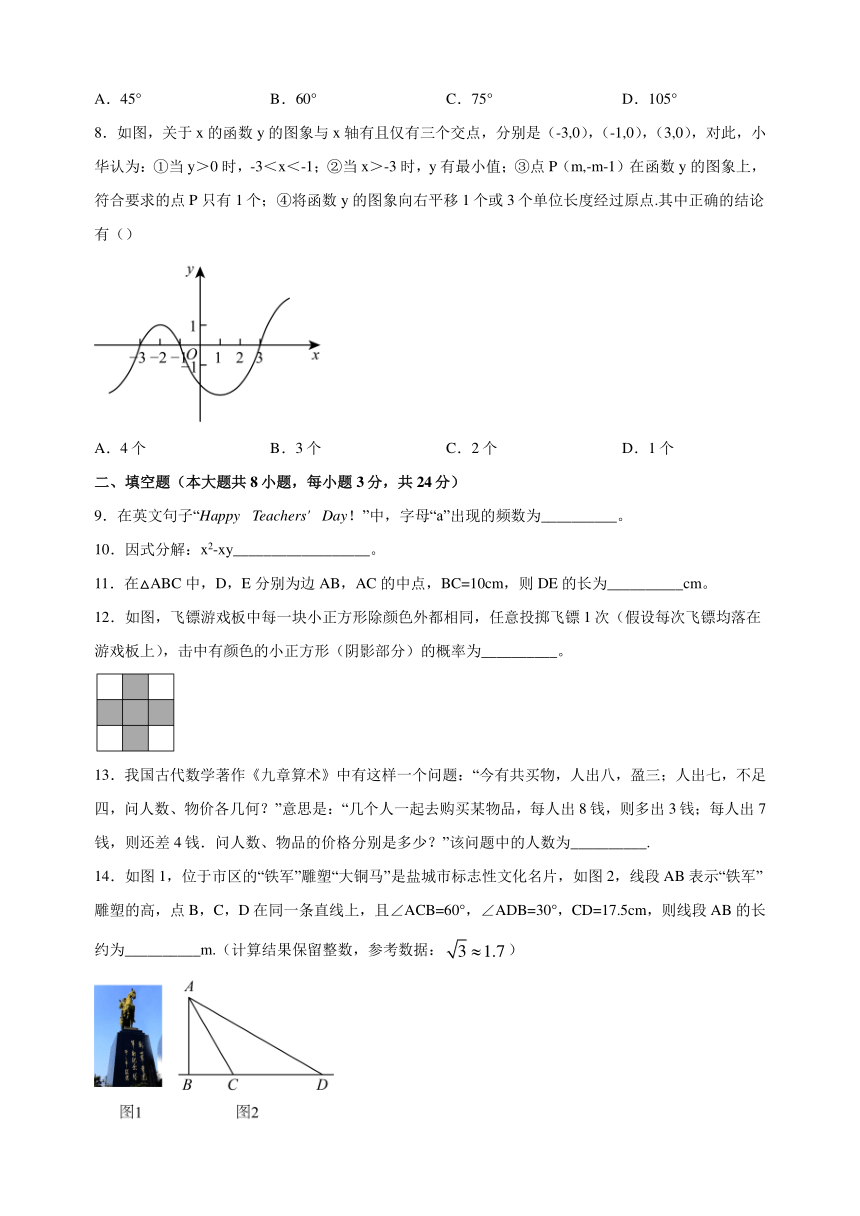
8．如图，关于x的函数y的图象与x轴有且仅有三个交点，分别是（-3,0），（-1,0），（3,0），对此，小华认为：①当y＞0时，-3＜x＜-1；②当x＞-3时，y有最小值；③点P（m,-m-1）在函数y的图象上，符合要求的点P只有1个；④将函数y的图象向右平移1个或3个单位长度经过原点.其中正确的结论有（）
A．4个 B．3个 C．2个 D．1个
二、填空题（本大题共8小题，每小题3分，共24分）
9．在英文句子“Happy Teachers' Day！”中，字母“a”出现的频数为__________。
10．因式分解：x2-xy__________________。
11．在△ABC中，D，E分别为边AB，AC的中点，BC=10cm，则DE的长为__________cm。
12．如图，飞镖游戏板中每一块小正方形除颜色外都相同，任意投掷飞镖1次（假设每次飞镖均落在游戏板上），击中有颜色的小正方形（阴影部分）的概率为__________。
13．我国古代数学著作《九章算术》中有这样一个问题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”意思是：“几个人一起去购买某物品，每人出8钱，则多出3钱；每人出7钱，则还差4钱．问人数、物品的价格分别是多少？”该问题中的人数为__________.
14．如图1，位于市区的“铁军”雕塑“大铜马”是盐城市标志性文化名片，如图2，线段AB表示“铁军”雕塑的高，点B，C，D在同一条直线上，且∠ACB=60°，∠ADB=30°，CD=17.5cm，则线段AB的长约为__________m.（计算结果保留整数，参考数据：）
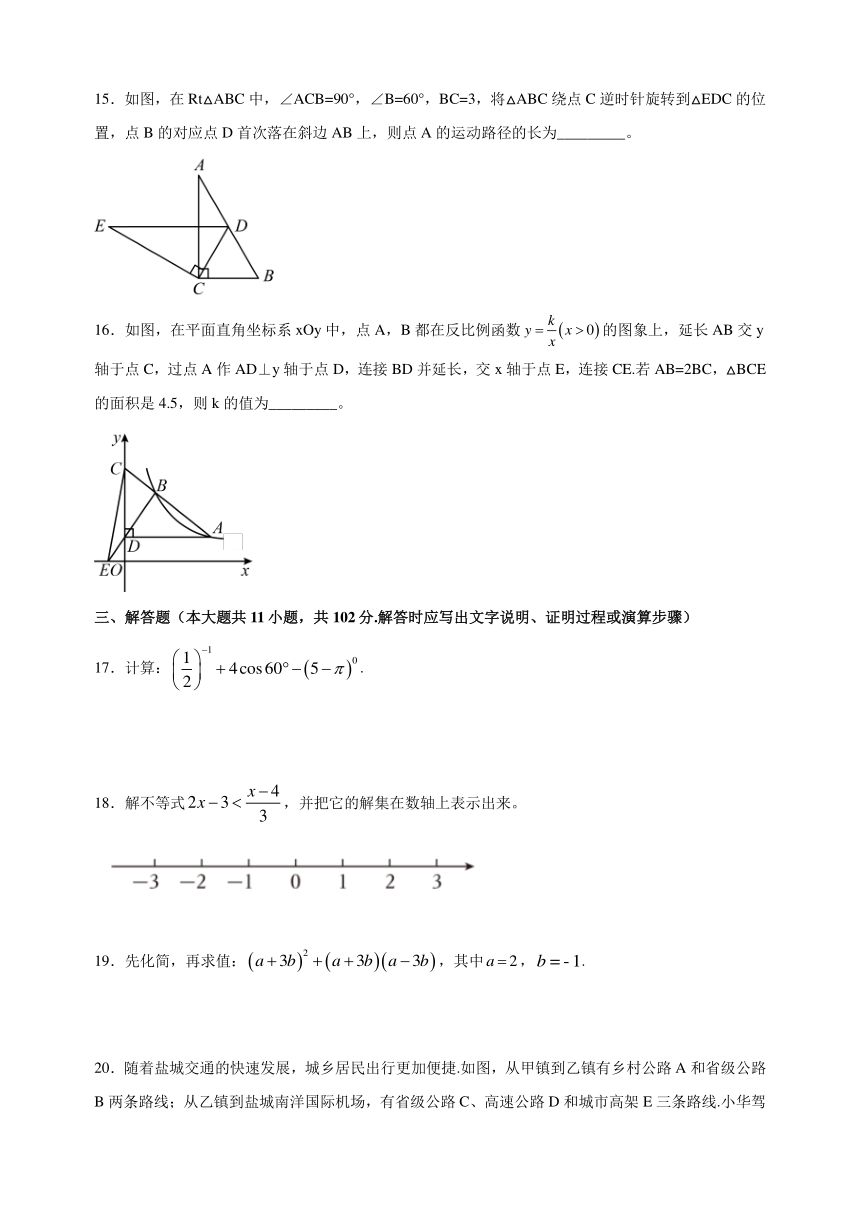
15．如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=3，将△ABC绕点C逆时针旋转到△EDC的位置，点B的对应点D首次落在斜边AB上，则点A的运动路径的长为_________。
16．如图，在平面直角坐标系xOy中，点A，B都在反比例函数的图象上，延长AB交y轴于点C，过点A作AD⊥y轴于点D，连接BD并延长，交x轴于点E，连接CE.若AB=2BC，△BCE的面积是4.5，则k的值为_________。
三、解答题（本大题共11小题，共102分.解答时应写出文字说明、证明过程或演算步骤）
17．计算：.
18．解不等式，并把它的解集在数轴上表示出来。
19．先化简，再求值：，其中，.
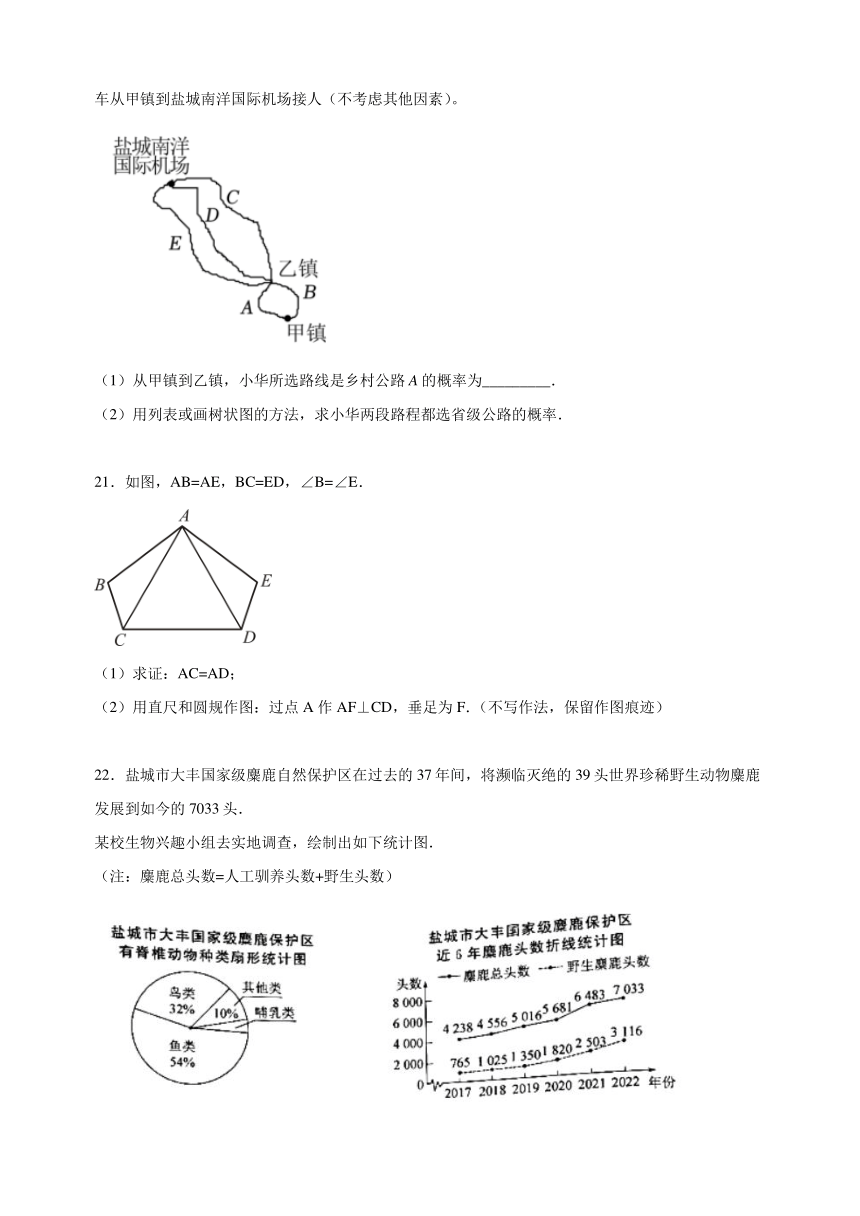
20．随着盐城交通的快速发展，城乡居民出行更加便捷.如图，从甲镇到乙镇有乡村公路A和省级公路B两条路线；从乙镇到盐城南洋国际机场，有省级公路C、高速公路D和城市高架E三条路线.小华驾车从甲镇到盐城南洋国际机场接人（不考虑其他因素）。
（1）从甲镇到乙镇，小华所选路线是乡村公路A的概率为_________．
（2）用列表或画树状图的方法，求小华两段路程都选省级公路的概率．
21．如图，AB=AE，BC=ED，∠B=∠E．
（1）求证：AC=AD；
（2）用直尺和圆规作图：过点A作AF⊥CD，垂足为F．（不写作法，保留作图痕迹）
22．盐城市大丰国家级麋鹿自然保护区在过去的37年间，将濒临灭绝的39头世界珍稀野生动物麋鹿发展到如今的7033头．
某校生物兴趣小组去实地调查，绘制出如下统计图．
（注：麋鹿总头数=人工驯养头数+野生头数）
解答下列问题：
（1）①在扇形统计图中，哺乳类所在扇形的圆心角度数为_______°；
②在折线统计图中，近6年野生麋鹿头数的中位数为_______头．
（2）填表：
年份 2017 2018 2019 2020 2021 2022
人工驯养麋鹿头数 3473 3531 3666 3861 _________ 3917
（3）结合以上的统计和计算，谈谈你对该保护区的建议或想法．
23．课堂上，老师提出了下面的问题：
已知，，，试比较M与N的大小．
小华：整式的大小比较可采用“作差法”.
老师：比较与的大小．
小华：∵，
∴．
老师：分式的大小比较能用“作差法”吗？
…
（1）请用“作差法”完成老师提出的问题．
（2）比较大小：__________．（填“＞”“=”或“＜”）
24．如图，在△ABC中，O是AC上（异于点A，C）的一点，⊙O恰好经过点A，B，AD⊥CB于点D，且AB平分∠CAD．
（1）判断BC与⊙O的位置关系，并说明理由；
（2）若AC=10，DC=8，求⊙O的半径长。
25．某校举行“二十大知识学习竞赛”活动，老师让班长小华到商店购买笔记本作为奖品．甲、乙两家商店每本硬面笔记本比软面笔记本都贵3元（单价均为整数）。
（1）若班长小华在甲商店购买，他发现用240元购买硬面笔记本与用195元购买软面笔记本的数量相同，求甲商店硬面笔记本的单价。
（2）若班长小华在乙商店购买硬面笔记本，乙商店给出了硬面笔记本的优惠条件（软面笔记本单价不变）：一次购买的数量少于30本，按原价售出；不少于30本按软面笔记本的单价售出．班长小华打算购买m本硬面笔记本（m为正整数），他发现再多购买5本的费用恰好与按原价购买的费用相同，求乙商店硬面笔记本的原价。
26．定义：若一次函数的图象与二次函数的图象有两个交点，并且都在坐标轴上，则称二次函数为一次函数的轴点函数．
初步理解】
（1）现有以下两个函数：①；②，其中，_________为函数的轴点函数．（填序号）
【尝试应用】
（2）函数（为常数，）的图象与轴交于点，其轴点函数与轴的另一交点为点.若，求的值．
【拓展延伸】
（3）如图，函数（为常数，）的图象与轴、轴分别交于，两点，在轴的正半轴上取一点，使得.以线段的长度为长、线段的长度为宽，在轴的上方作矩形.若函数（为常数，）的轴点函数的顶点在矩形的边上，求的值．
27综合与实践
【问题情境】
如图1，小华将矩形纸片ABCD先沿对角线BD折叠，展开后再折叠，使点B落在对角线BD上，点B的对应点记为B’，折痕与边AD，BC分别交于点E，F.
【活动猜想】
（1）如图2，当点B’与点D重合时，四边形BEDF是哪种特殊的四边形？答：_________.
【问题解决】
（2）如图3，当AB=4，AD=8，BF=3时，求证：点A’，B’，C在同一条直线上.
【深入探究】
（3）如图4，当AB与BC满足什么关系时，始终有A’B’与对角线AC平行？请说明理由.
（4）在（3）的情形下，设AC与BD，EF分别交于点O，P，试探究三条线段AP，B’D，EF之间满足的等量关系，并说明理由.
参考答案
一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，恰有一项是符合题目要求的）
1．B
【解析】根据小于0的数即为负数解答可得。
【详解】-2023是负数，2023和是正数，0既不是正数也不是负数，故选：B．
【点睛】本题主要考查正数和负数，熟练掌握负数的概念是解题的关键。
2．A
【解析】根据各象限内点的坐标特征解答。
【详解】点（1，2）所在的象限是第一象限．故选：A。
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（＋，＋）；第二象限（ ，＋）；第三象限（ ， ）；第四象限（＋， ）。
3．B
【解析】根据中心对称图形的定义进行逐一判断即可：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。
【详解】解：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。
由定义可判定A、C、D选项的图形不是中心对称图形，故不符合题意；
B选项的图形是中心对称图形，符合题意。
故选：B．
【点睛】本题主要考查了中心对称图形，熟知中心对称图形的定义是解题的关键。
4．D
【解析】根据三角形的三边关系“两边之和大于第三边，两边之差小于第三边”进行分析判断。
【详解】A、，不能构成三角形，故此选项不合题意；
B、，不能构成三角形，故此选项不合题意；
C、，不能构成三角形，故此选项不合题意；
D、，能构成三角形，故此选项符合题意．
故选：D．
【点睛】此题考查了三角形三边关系，看能否组成三角形的简便方法：看较小的两个数的和能否大于第三个数．
5．A
【解析】
【分析】绝对值大于1的数可以用科学记数法表示，一般形式为，为正整数，且比原数的整数位数少1，据此可以解答．
【详解】解：数据105000用科学记数法表示为．
故选：A．
【点睛】本题考查用科学记数法表示较大的数，熟练掌握科学记数法表示较大的数一般形式为，其中，是正整数，正确确定的值和的值是解题的关键．
6．D
【解析】
【分析】找到从上面看所得到图形即可，注意所有的看到的棱都应表现在俯视图中．
【详解】观察图形可知，该几何体的俯视图如下：
．
故选：D．
【点睛】本题考查了简单组合体的三视图的知识，俯视图是从物体的上面看得到的视图．
7．C
【解析】
【分析】根据平行线的性质得出，然后根据三角形内角和定理求解即可．
【详解】解：如图：设交于点，
∵，
∴，
∵，
∴．
故选：C．
【点睛】本题考查了三角形内角和定理、平行线的性质等知识点，熟练掌握平行线的性质是解题的关键．
8．C
【解析】
【分析】结合函数图象逐个分析即可．
【详解】由函数图象可得：
当时，或；故①错误；
当时，有最小值；故②正确；
点在直线上，直线与函数图象有3个交点，故③错误；
将函数的图象向右平移1个或3个单位长度经过原点，故④正确；
故选：C．
【点睛】本题考查了函数的图象与性质，一次函数图象，解题的关键是数形结合．
二、填空题（本大题共8小题，每小题3分，共24分）
9．
【解析】
【分析】根据频数定义可得答案．
【详解】在英文句子“Happy Teachers' Day！”中，字母“”出现的频数为，
故答案为：．
【点睛】此题主要考查了频数，关键是掌握频数是指每个对象出现的次数．
10．
【解析】
【分析】根据观察可知公因式x，因此提出x即可得出答案．
【详解】解：x2－xy= x(x－y).
故答案：
【点睛】提公因式法因式分解是本题的考点，通过观察正确找出公因式是解题的关键.
11．
【解析】
【分析】由于、分别为、边上的中点，那么是的中位线，根据三角形中位线定理可求．
【详解】如图所示，
、分别为、边上的中点，
是的中位线，
；
又∵，
∴；
故答案为：．
【点睛】本题考查了三角形中位线定理．三角形的中位线等于第三边的一半．
12．
【解析】
【分析】根据几何概率的求法：飞镖落在阴影部分的概率就是阴影区域的面积与总面积的比值．
【详解】解：设小正方形的边长为1，则总面积为9，其中阴影部分面积为5，
∴飞镖落在阴影部分的概率是，
故答案为：．
【点睛】本题考查了几何概率的求法，解题的关键是根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
13．7人
【解析】
【分析】设共有x人，价格为y钱，根据题意列出二元一次方程组即可求解．
【详解】解：设共有x人，价格为y钱，依题意得：
，
解得：，
答：物品价格为53钱，共同购买该物品的人数有7人,
故答案为：7．
【点睛】此题主要考查二元一次方程组的应用，解题的关键是根据题意列出方程组即可求解．
14．
【解析】
【分析】由，可得，可推得，由三角函数求出即可．
【详解】∵，，，
∴，
∴，
又∵，
∴，
∵，
∴
解得，
故答案为：．
【点睛】此题主要考查了解直角三角形的应用，正确得出的长是解题关键．
15．
【解析】
【分析】首先证明是等边三角形，再根据弧长公式计算即可．
【详解】解：在中，∵，，，
∴，
由旋转的性质得，，
，
∴是等边三角形，
∴，
∴点的运动路径的长为．
故答案为：．
【点睛】本题考查了旋转变换，含直角三角形的性质，等边三角形的判定和性质，弧长公式等知识，解题的关键是证明是等边三角形．
16．6
【解析】
【分析】过点B作于点F，连接，设点A的坐标为，点B的坐标为，则，证明，则，得到，根据，进一步列式即可求出k的值.
【详解】解：过点B作于点F，连接，设点A的坐标为，点B的坐标为，则，
∵，
∴，
∵轴于点，
∴，
∴，
∴，
∴，
∴，
∵，面积是，
∴，
∴，
∴，
则，
即，
解得，
故答案为：6
【点睛】此题考查反比例函数的图象和性质、相似三角形的判定和性质等知识，求出是解题的关键.
三、解答题（本大题共11小题，共102分.解答时应写出文字说明、证明过程或演算步骤）
17．
【解析】
【分析】直接利用负整数指数幂的性质、特殊角的三角函数值、零指数幂分别化简，进而得出答案．
【详解】原式．
【点睛】此题主要考查了实数的运算，正确化简各数是解题关键．
18．，数轴见详解
【解析】
【分析】根据解一元一次不等式的步骤解答即可．
【详解】
去分母得：，
去括号得：，
移项得：，
合并同类项得：，
系数化为1：．
在数轴上可表示为：
．
【点睛】本题考查了解一元一次不等式，在数轴上表示不等式的解集的应用，能求出不等式的解集是解此题的关键，难度适中．
19．，
【解析】
【分析】根据完全平方公式和平方差公式展开后化简，最后代入求值即可．
【详解】
当，时，原式．
【点睛】本题考查整式混合运算的化简求值，解题的关键是根据完全平方公式和平方差公式展开．
20．（1）（2）
【解析】
【分析】（1）根据概率公式计算即可；
（2）列表表示出所有的可能性，再根据概率公式计算即可．
【小问1详解】
从甲镇到乙镇，小华所选路线是乡村公路A的概率为，
故答案为：．
【小问2详解】
列表如下：
C D E
A AC AD AE
B BC BD BE
共有6种等可能的结果，其中两段路程都选省级公路只有，共1种，
∴小华两段路程都选省级公路的概率．
【点睛】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率．
21．（1）见解析（2）见解析
【解析】
【分析】（1）根据边角边证明即可证明结论成立；
（2）根据过直线外一点向直线最垂线的作法得出即可．
【小问1详解】
证明：∵，，，
∴，
∴；
【小问2详解】
解：所作图形如图，
．
【点睛】本题主要考查了全等三角形的判定和性质，过直线外一点向直线最垂线的作法，熟练记忆正确作法是解题关键．
22．（1），（2）（3）见解析
【解析】
【分析】（1）先计算哺乳类所占百分比，再计算该部分扇形圆心角的度数；
（2）先排序，再计算中间的两个数的平均数；
（3）从人工驯养和野生保护两个方面表述即可．
【小问1详解】
解：①在扇形统计图中，哺乳类所占的百分比为：，
∴哺乳类所在扇形的圆心角度数为：；
②在折线统计图中，近6年野生麋鹿头数按从小到大顺序排序为：
，
近6年野生麋鹿头数的中位数为，
故答案为：，；
【小问2详解】
解：，
故答案为：；
【小问3详解】
加强对野生麋鹿的保护的同时，提高人工驯养的技术．
【点睛】本题考查了扇形统计图和拆线统计图，中位数，掌握从图形中获取信息的方法是解题的关键．
23．（1）（2）
【解析】
（1）根据作差法求的值即可得出答案；
（2）根据作差法求的值即可得出答案．
【小问1详解】
解：，
，
，
；
【小问2详解】
解：，
．
故答案为：．
【点睛】本题考查分式运算的应用，解题关键是理解材料，通过作差法求解，掌握分式运算的方法．
24．（1）见解析（2）的半径长为．
【解析】
【分析】（1）连接，证明，即可证得，从而证得是圆的切线；
（2）设，则，利用勾股定理求得，推出，利用相似三角形的性质列得比例式，据此求解即可．
【小问1详解】
证明：连接，如下图所示，
∵是的平分线，
∴，
又∵，
∴，
∴，
∴，
∴，即，
又∵过半径的外端点B，
∴与相切；
【小问2详解】
解：设，则，
∵在中，，，，
∴，
∵，
∴，
∴，即，
解得．
故的半径长为．
【点睛】本题考查了切线的判定，相似三角形的判定和性质，以及勾股定理，熟练掌握切线的判定是解本题的关键．
25．（1）甲商店硬面笔记本的单价为16元
（2）乙商店硬面笔记本的原价18元
【解析】
【分析】（1）根据“硬面笔记本数量=软面笔记本数量”列出分式方程，求解检验即可；
（2）设乙商店硬面笔记本原价为a元，则软面笔记本的单价为元，由再多购买5本的费用恰好与按原价购买的费用相同可得，再根据且m，均为正整数，即可求解．
【小问1详解】
解：设硬面笔记本的单价为x元，则软面笔记本的单价为元，根据题意得
，
解得，
经检验，是原方程的根，且符合题意，
故甲商店硬面笔记本的单价为16元；
【小问2详解】
设乙商店硬面笔记本的原价为a元，则软面笔记本的单价为元，
由题意可得，
解得，
根据题意得，
解得，
为正整数，
，，，，，分别代入，
可得，，，，，
由单价均为整数可得，
故乙商店硬面笔记本的原价18元．
【点睛】本题考查了分式方程的应用以及二元一次方程的应用，解题的关键是找准等量关系，正确列出相应方程．
26．（1）①；（2）或；（3）或或
【解析】
【分析】（1）求出函数与坐标轴的交点，再判断这两个点在不在二次函数图象上即可；
（2）求出函数与坐标轴的交点，再由求出点坐标，代入二次函数解析式计算即可；
（3）先求出，的坐标，再根据的顶点在矩形的边上分类讨论即可．
【详解】（1）函数交轴于，交轴于，
∵点、都在函数图象上
∴①为函数的轴点函数；
∵点不在函数图象上
∴②不是函数的轴点函数；
故答案为：①；
（2）函数交轴于，交轴于，
∵函数的轴点函数
∴和都在上，
∵
∴
∵，
∴
∴或
当时，把代入得
，解得，
当时，把代入得
，解得，
综上，或；
（3）函数交轴于，交轴于，
∵，以线段的长度为长、线段的长度为宽，在轴的上方作矩形
∴，，,
∵函数（为常数，）的轴点函数
∴和在上
∴，整理得
∴
∴的顶点坐标为，
∵函数的顶点在矩形的边上
∴可以分三种情况讨论：当与重合时；当在上时；当在上时；
当与重合时，即，解得；
当在上时，，整理得，解得
此时二次函数开口向下，则
∴整理得：，
由整理得，
∴
解得，
∴，
当在上时，，整理得，解得
∴
此时对称轴左边y随x的增大而增大，
∴
∴整理得：
∴代入、后成立
∴，
综上所述，或或
【点睛】本题综合考查一次函数与二次函数，解题的关键是理解轴点函数的定义．
27．（1）菱形；（2）证明见解答；（3），证明见解析；（4），理由见解析
【解析】
【分析】（1）由折叠可得：，，再证得，可得，利用菱形的判定定理即可得出答案；
（2）设与交于点，过点作于，利用勾股定理可得，再证明，可求得，进而可得，再由，可求得，，，运用勾股定理可得，运用勾股定理逆定理可得，进而可得，即可证得结论；
（3）设，则，利用折叠的性质和平行线性质可得：，再运用三角形内角和定理即可求得，利用解直角三角形即可求得答案；
（4）过点作于，设交于，设，，利用解直角三角形可得，，即可得出结论．
【详解】解：（1）当点与点重合时，四边形是菱形．
理由：设与交于点，如图，
由折叠得：，，
，
四边形是矩形，
，
，
，
，
四边形是菱形．
故答案为：菱形．
（2）证明：四边形是矩形，，，，
，，，
，
，
如图，设与交于点，过点作于，
由折叠得：，，，
，
，
，
，即，
，
，
，，
，
，即，
，，
，
，
，，
，
，
，
点，，在同一条直线上．
（3）当时，始终有与对角线平行．
理由：如图，设、交于点，
四边形是矩形，
，，
，
设，
则，
由折叠得：，，
，，
，
，
，
，
，即，
，
，
，
；
（4），理由如下：
如图，过点作于，设交于，
由折叠得：，，，
设，，
由（3）得：，
，
，
，，
，
四边形是矩形，
，，，
，
，
，
，
，
，
，
，
，
，
，
即．
【点睛】本题是四边形综合题，考查了矩形的性质和判定，菱形的判定，勾股定理，直角三角形性质，等腰三角形性质，平行线性质，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等，涉及知识点多，综合性强，难度较大．