2023-2024学年初中数学人教版八年级下册第十八章 平行四边形 单元练习 (含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册第十八章 平行四边形 单元练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:01:00 | ||
图片预览



文档简介
第十八章 平行四边形 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题2分,满分20分)
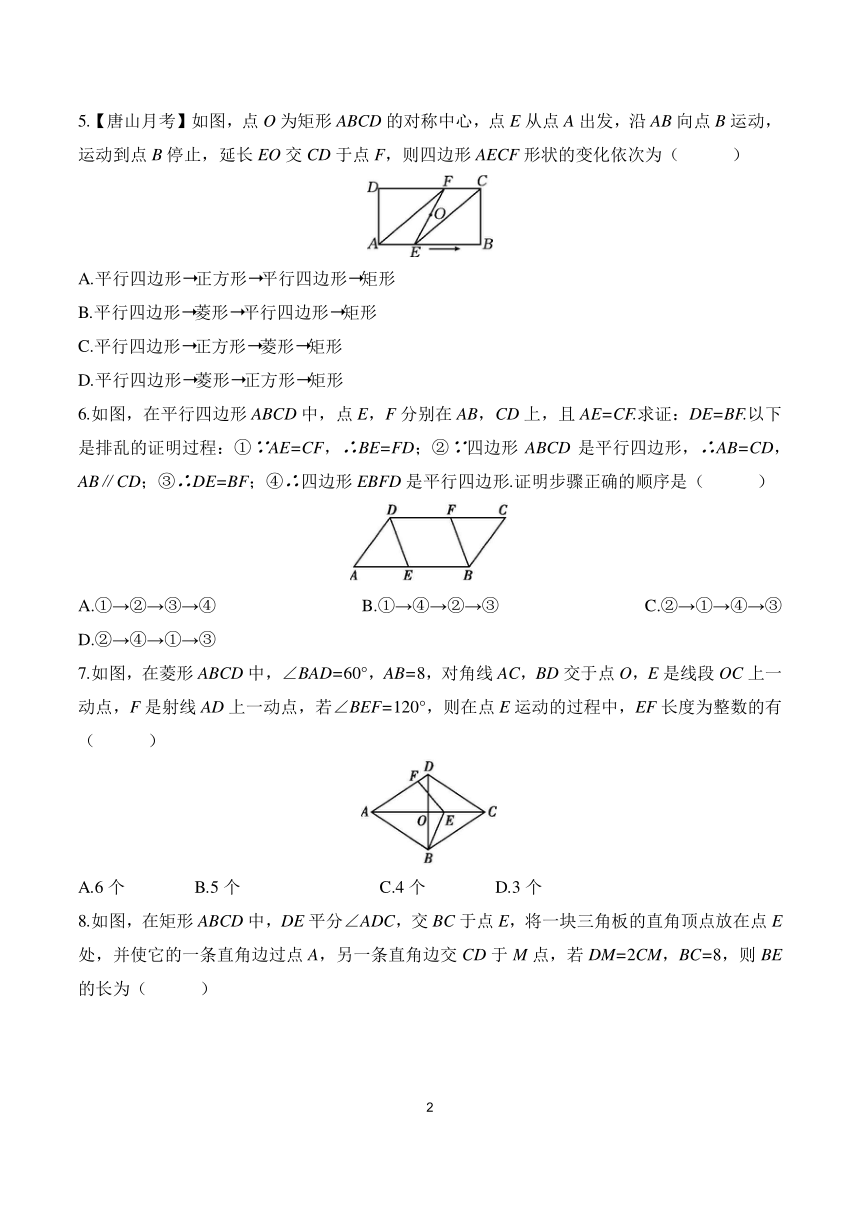
1.【教材P61T12变式】如图,在矩形ABCD中,A(-3,2),B(3,2),C(3,-1),则点D的坐标为( )
A.(-2,-1) B.(4,-1) C.(-3,-2) D.(-3,-1)
2.关于 ABCD的叙述,正确的是( )
A.若AC=BD,则 ABCD是菱形
B.若AB=AD,则 ABCD是矩形
C.若AB⊥BC,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是菱形
3.如图,在菱形ABCD中,∠B=60°,AB=3,E是BC边上的一个动点(点E与点C不重合),F,G分别是AE,CE的中点,则线段FG的长为( )
A. B.3 C.2 D.2
4.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的是( )
A.∠DCB=∠B B.BC=BD C.AD=BD D.∠ACD=∠BDC
5.【唐山月考】如图,点O为矩形ABCD的对称中心,点E从点A出发,沿AB向点B运动,运动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形 正方形 平行四边形 矩形
B.平行四边形 菱形 平行四边形 矩形
C.平行四边形 正方形 菱形 矩形
D.平行四边形 菱形 正方形 矩形
6.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,且AE=CF.求证:DE=BF.以下是排乱的证明过程:①∵AE=CF,∴BE=FD;②∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD;③∴DE=BF;④∴四边形EBFD是平行四边形.证明步骤正确的顺序是( )
A.①→②→③→④ B.①→④→②→③ C.②→①→④→③ D.②→④→①→③
7.如图,在菱形ABCD中,∠BAD=60°,AB=8,对角线AC,BD交于点O,E是线段OC上一动点,F是射线AD上一动点,若∠BEF=120°,则在点E运动的过程中,EF长度为整数的有( )
A.6个 B.5个 C.4个 D.3个
8.如图,在矩形ABCD中,DE平分∠ADC,交BC于点E,将一块三角板的直角顶点放在点E处,并使它的一条直角边过点A,另一条直角边交CD于M点,若DM=2CM,BC=8,则BE的长为( )
A.3 B. C. D.2
9.如图,正方形ABCD的边长为4,P是对角线BD上一点,PE∥CD交BC于点E,PF∥BC交CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF.其中正确结论的序号为( )
A.①②④ B.①③④ C.②④ D.②③
10.【邯郸月考】现有一张纸片,∠BAF=∠ABC=∠CDE=∠FED=∠AFE=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示,将它们沿着虚线剪开后,分别要拼一个与原来面积相等的正方形,则( )
A.甲、乙都不可以 B.甲不可以,乙可以 C.甲、乙都可以 D.甲可以,乙不可以
二、填空题(本大题共5小题,每小题3分,满分15分)
11.如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件_______,使四边形BEFD为矩形.(填一个即可)
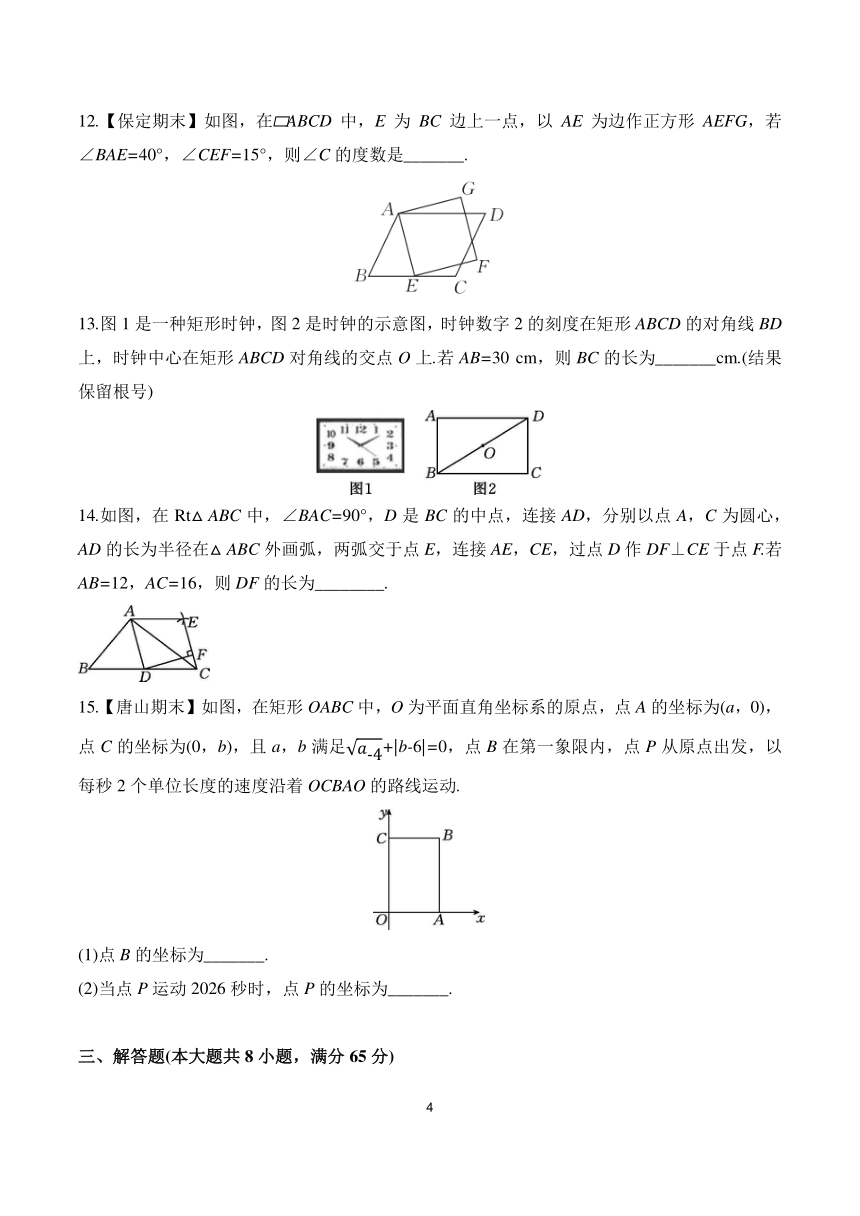
12.【保定期末】如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠C的度数是_______.
13.图1是一种矩形时钟,图2是时钟的示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB=30 cm,则BC的长为_______cm.(结果保留根号)
14.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,连接AD,分别以点A,C为圆心,AD的长为半径在△ABC外画弧,两弧交于点E,连接AE,CE,过点D作DF⊥CE于点F.若AB=12,AC=16,则DF的长为________.
15.【唐山期末】如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着OCBAO的路线运动.
(1)点B的坐标为_______.
(2)当点P运动2026秒时,点P的坐标为_______.
三、解答题(本大题共8小题,满分65分)
16.(6分)如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
17.(6分)如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,EF过点O交AB于点E,交CD于点F,且OE=OF.
(1)求证:四边形ABCD是平行四边形.
(2)若S四边形AEFD=5,则S四边形ABCD=________.
18.(6分)如图,O是△ABC内一点,连接OB,OC,线段AB,OB,OC,AC的中点分别为D,E,F,G.
(1)判断四边形DEFG的形状,并说明理由.
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
19.(8分)定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,若P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,若P是菱形ABCD对角线上的任意一点,求证:P为菱形ABCD的一个“互补点”.
20.(9分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度1 cm/s向C,A运动.
(1)四边形DEBF是平行四边形吗 判断并说明理由.
(2)若BD=12 cm,AC=16 cm,当运动时间t为何值时,四边形DEBF是矩形
21.(9分)在△ABC中,AB=AC,D,O分别是BC,AC边的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形.
(2)如图2,点F在线段CE上,连接AF,DF,在不添加任何字母和辅助线的情况下,请直接写出四个与四边形ABDF面积相等的三角形或四边形.
22.(9分)如图,在平行四边形ABCD中,G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.
23.(12分)如图,在 ABCD中,G,H分别是AD,BC的中点,E,O,F分别是对角线BD上的四等分点,顺次连接G,E,H,F.
(1)求证:四边形GEHF是平行四边形.
(2)当 ABCD满足_______条件时,四边形GEHF是菱形.
(3)若BD=2AB.
①探究四边形GEHF的形状,并说明理由.
②当AB=2,∠ABD=120°时,求出四边形GEHF的面积.
参考答案
1.D 2.D
3.A 【解析】如图,连接AC,∵四边形ABCD是菱形,
∴BC=AB=3.
∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=3.
∵F,G分别是AE,CE的中点,∴FG是△ACE的中位线,
∴FG=AC=.
4.B 5.B 6.C 7.B 8.D 9.A
10.C 【解析】如图1,将△AEF移至①处,△DEH移至②处,四边形GCHE移至③处,即可得到一个与原来面积相等的正方形;
如图2,将△ABG,△AHG,△HGF分别移至①②③处,即可得到一个与原来面积相等的正方形.故甲、乙方案都可以.
11.AB⊥BC 12.115°
13.30 【解析】如图,过点O作OE⊥CD,OF⊥AD,垂足分别为E,F,由题意知∠FOD=2∠DOE,
∵∠FOD+∠DOE=90°,
∴∠DOE=30°,∠FOD=60°.
在矩形ABCD中,∠C=90°,CD=AB=30 cm,易得OE∥BC,
∴∠DBC=∠DOE=30°,∴BD=60 cm,
∴BC=30 cm.
14. 【解析】
在Rt△ABC中,∠BAC=90°,D是BC的中点,
∴AD=CD,由题意得AE=EC=AD,∴AE=EC=AD=CD,∴四边形ADCE是菱形.
如图,过点A作AH⊥BC于点H,
∵AB=12,AC=16,
∴BC==20.
∵S△ABC=AB·AC=BC·AH,
∴AH===.
∵S菱形ADCE=EC·DF=CD·AH,CD=CE,
∴DF=AH=.
15.(1)(4,6) (2)(4,4)
【解析】(1)由题意,可知点B的坐标为(a,b).
∵a,b满足+|b-6|=0,
∴a-4=0,b-6=0,解得a=4,b=6,
∴点B的坐标为(4,6).
(2)由点B的坐标为(4,6),得矩形OABC的周长为2×(4+6)=20,易知点P每隔10秒就会回到起点O,
∵2026÷10=202……6,∴当点P运动2026秒时会循环202次,且又运动6秒,此时点P在AB上,点P的纵坐标为4,∴点P的坐标为(4,4).
16.【证明】∵四边形ABCD是菱形,
∴AD=CD,AB=BC,∠A=∠C.
∵∠ABE=∠CBF,
∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,
∴DE=DF.
17.【解析】(1)证明:∵AB∥CD,
∴∠BAC=∠DCA,∠ABD=∠CDB.
在△AOE和△COF中,
∴△AOE≌△COF(AAS),
∴AE=CF,
同理可证△BEO≌△DFO,
∴BE=DF,
∴AB=CD.
∵AB∥CD,
∴四边形ABCD是平行四边形.
(2)∵S四边形AEFD=5,
∴S四边形ABCD=10.
故答案为10.
18.【解析】(1)四边形DEFG是平行四边形.
理由:∵E,F分别为线段OB,OC的中点,
∴EF=BC,EF∥BC.
同理DG=BC,DG∥BC,∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形.
(2)∵∠OBC和∠OCB互余,∴∠BOC=90°.
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
19.【解析】(1)∵如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,
∴∠BPC=180°-∠APD=180°-63°=117°,即∠BPC=117°.
(2)证明:如图2,连接AP,CP.
∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.
在△ADP与△CDP中,
∴△ADP≌△CDP(SAS),∴∠APD=∠CPD.
又∵∠APB+∠APD=180°,
∴∠APB+∠CPD=180°,
即P为菱形ABCD的一个“互补点”.
20.【解析】(1)是.
理由:在平行四边形ABCD中,OD=OB,OA=OC.
∵E,F两点移动的速度相同,即AE=CF,∴OE=OF.又∵OD=OB,
∴四边形DEBF是平行四边形.
(2)∵矩形的对角线相等,∴当EF=12 cm时,其为矩形,
即AE=CF=×(16-12)=2,
所以当t=2 s或16-2=14 s时,四边形DEBF是矩形.
21.【解析】(1)证明:∵AE∥BC,∴∠EAO=∠DCO.
∵O是AC的中点,∴OA=OC.
在△OAE和△OCD中,
∴△OAE≌△OCD(ASA),∴AE=CD,
∴四边形ADCE是平行四边形.
∵AB=AC,D是BC的中点,∴AD⊥BC,
∴∠ADC=90°,∴四边形ADCE是矩形.
(2)四边形ABDE,四边形ADCE,△ABC,△BCE,理由如下:
由(1)得四边形ADCE是矩形,∴AD∥CE,△ACD的面积=△ACE的面积,
∴△ADE的面积=△ADF的面积,∴四边形ABDE的面积=四边形ABDF的面积.
∵D是BC的中点,AE∥CD,∴△BCE的面积=△ABC的面积=2△ACD的面积=2△ACE的面积,
∴△BCE的面积=△ABC的面积=四边形ADCE的面积=四边形ABDF的面积.
22.【解析】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠GAE=∠HCF.
∵G,H分别是AB,CD的中点,∴AG=CH.
在△AGE和△CHF中,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,∴∠GEF=∠HFE,∴GE∥HF.
又∵GE=HF,∴四边形EGFH是平行四边形.
(2)如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵BD=12,∴OB=OD=6.
∵AE=CF,OA=OC,∴OE=OF.
∵AE=EF-CF,∴AE+CF=EF,
∴2AE=EF=2OE,∴AE=OE.
又∵G是AB的中点,∴EG是△ABO的中位线,
∴EG=OB=3.
23.【解析】(1)证明:连接AC,如图1所示.
∵四边形ABCD是平行四边形,E,O,F分别是对角线BD上的四等分点,
∴AC一定经过点O,∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点.
∵G是AD的中点,∴GF为△AOD的中位线,
∴GF∥OA,GF=OA.
同理可得EH∥OC,EH=OC,∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形.
(2)当 ABCD满足AB⊥BD条件时,四边形GEHF是菱形.理由如下:
连接GH,如图2,则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH.
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形.
(3)①四边形GEHF是矩形.
理由:由(2)得四边形ABHG是平行四边形,
∴GH=AB.
∵BD=2AB,∴AB=BD=EF,∴GH=EF,
∴四边形GEHF是矩形.
②如图3,作AM⊥BD于点M,GN⊥BD于点N,则AM∥GN.
∵G是AD的中点,∴GN是△ADM的中位线,
∴GN=AM.
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=AB=1,AM=BM=,∴GN=.
∵BD=2AB=4,∴EF=BD=2,
∴△EFG的面积=EF·GN=×2×=,
∴四边形GEHF的面积=2△EFG的面积=.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题2分,满分20分)
1.【教材P61T12变式】如图,在矩形ABCD中,A(-3,2),B(3,2),C(3,-1),则点D的坐标为( )
A.(-2,-1) B.(4,-1) C.(-3,-2) D.(-3,-1)
2.关于 ABCD的叙述,正确的是( )
A.若AC=BD,则 ABCD是菱形
B.若AB=AD,则 ABCD是矩形
C.若AB⊥BC,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是菱形
3.如图,在菱形ABCD中,∠B=60°,AB=3,E是BC边上的一个动点(点E与点C不重合),F,G分别是AE,CE的中点,则线段FG的长为( )
A. B.3 C.2 D.2
4.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的是( )
A.∠DCB=∠B B.BC=BD C.AD=BD D.∠ACD=∠BDC
5.【唐山月考】如图,点O为矩形ABCD的对称中心,点E从点A出发,沿AB向点B运动,运动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形 正方形 平行四边形 矩形
B.平行四边形 菱形 平行四边形 矩形
C.平行四边形 正方形 菱形 矩形
D.平行四边形 菱形 正方形 矩形
6.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,且AE=CF.求证:DE=BF.以下是排乱的证明过程:①∵AE=CF,∴BE=FD;②∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD;③∴DE=BF;④∴四边形EBFD是平行四边形.证明步骤正确的顺序是( )
A.①→②→③→④ B.①→④→②→③ C.②→①→④→③ D.②→④→①→③
7.如图,在菱形ABCD中,∠BAD=60°,AB=8,对角线AC,BD交于点O,E是线段OC上一动点,F是射线AD上一动点,若∠BEF=120°,则在点E运动的过程中,EF长度为整数的有( )
A.6个 B.5个 C.4个 D.3个
8.如图,在矩形ABCD中,DE平分∠ADC,交BC于点E,将一块三角板的直角顶点放在点E处,并使它的一条直角边过点A,另一条直角边交CD于M点,若DM=2CM,BC=8,则BE的长为( )
A.3 B. C. D.2
9.如图,正方形ABCD的边长为4,P是对角线BD上一点,PE∥CD交BC于点E,PF∥BC交CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF.其中正确结论的序号为( )
A.①②④ B.①③④ C.②④ D.②③
10.【邯郸月考】现有一张纸片,∠BAF=∠ABC=∠CDE=∠FED=∠AFE=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示,将它们沿着虚线剪开后,分别要拼一个与原来面积相等的正方形,则( )
A.甲、乙都不可以 B.甲不可以,乙可以 C.甲、乙都可以 D.甲可以,乙不可以
二、填空题(本大题共5小题,每小题3分,满分15分)
11.如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件_______,使四边形BEFD为矩形.(填一个即可)
12.【保定期末】如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠C的度数是_______.
13.图1是一种矩形时钟,图2是时钟的示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB=30 cm,则BC的长为_______cm.(结果保留根号)
14.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,连接AD,分别以点A,C为圆心,AD的长为半径在△ABC外画弧,两弧交于点E,连接AE,CE,过点D作DF⊥CE于点F.若AB=12,AC=16,则DF的长为________.
15.【唐山期末】如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着OCBAO的路线运动.
(1)点B的坐标为_______.
(2)当点P运动2026秒时,点P的坐标为_______.
三、解答题(本大题共8小题,满分65分)
16.(6分)如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
17.(6分)如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,EF过点O交AB于点E,交CD于点F,且OE=OF.
(1)求证:四边形ABCD是平行四边形.
(2)若S四边形AEFD=5,则S四边形ABCD=________.
18.(6分)如图,O是△ABC内一点,连接OB,OC,线段AB,OB,OC,AC的中点分别为D,E,F,G.
(1)判断四边形DEFG的形状,并说明理由.
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
19.(8分)定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,若P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,若P是菱形ABCD对角线上的任意一点,求证:P为菱形ABCD的一个“互补点”.
20.(9分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度1 cm/s向C,A运动.
(1)四边形DEBF是平行四边形吗 判断并说明理由.
(2)若BD=12 cm,AC=16 cm,当运动时间t为何值时,四边形DEBF是矩形
21.(9分)在△ABC中,AB=AC,D,O分别是BC,AC边的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形.
(2)如图2,点F在线段CE上,连接AF,DF,在不添加任何字母和辅助线的情况下,请直接写出四个与四边形ABDF面积相等的三角形或四边形.
22.(9分)如图,在平行四边形ABCD中,G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.
23.(12分)如图,在 ABCD中,G,H分别是AD,BC的中点,E,O,F分别是对角线BD上的四等分点,顺次连接G,E,H,F.
(1)求证:四边形GEHF是平行四边形.
(2)当 ABCD满足_______条件时,四边形GEHF是菱形.
(3)若BD=2AB.
①探究四边形GEHF的形状,并说明理由.
②当AB=2,∠ABD=120°时,求出四边形GEHF的面积.
参考答案
1.D 2.D
3.A 【解析】如图,连接AC,∵四边形ABCD是菱形,
∴BC=AB=3.
∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=3.
∵F,G分别是AE,CE的中点,∴FG是△ACE的中位线,
∴FG=AC=.
4.B 5.B 6.C 7.B 8.D 9.A
10.C 【解析】如图1,将△AEF移至①处,△DEH移至②处,四边形GCHE移至③处,即可得到一个与原来面积相等的正方形;
如图2,将△ABG,△AHG,△HGF分别移至①②③处,即可得到一个与原来面积相等的正方形.故甲、乙方案都可以.
11.AB⊥BC 12.115°
13.30 【解析】如图,过点O作OE⊥CD,OF⊥AD,垂足分别为E,F,由题意知∠FOD=2∠DOE,
∵∠FOD+∠DOE=90°,
∴∠DOE=30°,∠FOD=60°.
在矩形ABCD中,∠C=90°,CD=AB=30 cm,易得OE∥BC,
∴∠DBC=∠DOE=30°,∴BD=60 cm,
∴BC=30 cm.
14. 【解析】
在Rt△ABC中,∠BAC=90°,D是BC的中点,
∴AD=CD,由题意得AE=EC=AD,∴AE=EC=AD=CD,∴四边形ADCE是菱形.
如图,过点A作AH⊥BC于点H,
∵AB=12,AC=16,
∴BC==20.
∵S△ABC=AB·AC=BC·AH,
∴AH===.
∵S菱形ADCE=EC·DF=CD·AH,CD=CE,
∴DF=AH=.
15.(1)(4,6) (2)(4,4)
【解析】(1)由题意,可知点B的坐标为(a,b).
∵a,b满足+|b-6|=0,
∴a-4=0,b-6=0,解得a=4,b=6,
∴点B的坐标为(4,6).
(2)由点B的坐标为(4,6),得矩形OABC的周长为2×(4+6)=20,易知点P每隔10秒就会回到起点O,
∵2026÷10=202……6,∴当点P运动2026秒时会循环202次,且又运动6秒,此时点P在AB上,点P的纵坐标为4,∴点P的坐标为(4,4).
16.【证明】∵四边形ABCD是菱形,
∴AD=CD,AB=BC,∠A=∠C.
∵∠ABE=∠CBF,
∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,
∴DE=DF.
17.【解析】(1)证明:∵AB∥CD,
∴∠BAC=∠DCA,∠ABD=∠CDB.
在△AOE和△COF中,
∴△AOE≌△COF(AAS),
∴AE=CF,
同理可证△BEO≌△DFO,
∴BE=DF,
∴AB=CD.
∵AB∥CD,
∴四边形ABCD是平行四边形.
(2)∵S四边形AEFD=5,
∴S四边形ABCD=10.
故答案为10.
18.【解析】(1)四边形DEFG是平行四边形.
理由:∵E,F分别为线段OB,OC的中点,
∴EF=BC,EF∥BC.
同理DG=BC,DG∥BC,∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形.
(2)∵∠OBC和∠OCB互余,∴∠BOC=90°.
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
19.【解析】(1)∵如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,
∴∠BPC=180°-∠APD=180°-63°=117°,即∠BPC=117°.
(2)证明:如图2,连接AP,CP.
∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.
在△ADP与△CDP中,
∴△ADP≌△CDP(SAS),∴∠APD=∠CPD.
又∵∠APB+∠APD=180°,
∴∠APB+∠CPD=180°,
即P为菱形ABCD的一个“互补点”.
20.【解析】(1)是.
理由:在平行四边形ABCD中,OD=OB,OA=OC.
∵E,F两点移动的速度相同,即AE=CF,∴OE=OF.又∵OD=OB,
∴四边形DEBF是平行四边形.
(2)∵矩形的对角线相等,∴当EF=12 cm时,其为矩形,
即AE=CF=×(16-12)=2,
所以当t=2 s或16-2=14 s时,四边形DEBF是矩形.
21.【解析】(1)证明:∵AE∥BC,∴∠EAO=∠DCO.
∵O是AC的中点,∴OA=OC.
在△OAE和△OCD中,
∴△OAE≌△OCD(ASA),∴AE=CD,
∴四边形ADCE是平行四边形.
∵AB=AC,D是BC的中点,∴AD⊥BC,
∴∠ADC=90°,∴四边形ADCE是矩形.
(2)四边形ABDE,四边形ADCE,△ABC,△BCE,理由如下:
由(1)得四边形ADCE是矩形,∴AD∥CE,△ACD的面积=△ACE的面积,
∴△ADE的面积=△ADF的面积,∴四边形ABDE的面积=四边形ABDF的面积.
∵D是BC的中点,AE∥CD,∴△BCE的面积=△ABC的面积=2△ACD的面积=2△ACE的面积,
∴△BCE的面积=△ABC的面积=四边形ADCE的面积=四边形ABDF的面积.
22.【解析】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠GAE=∠HCF.
∵G,H分别是AB,CD的中点,∴AG=CH.
在△AGE和△CHF中,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,∴∠GEF=∠HFE,∴GE∥HF.
又∵GE=HF,∴四边形EGFH是平行四边形.
(2)如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵BD=12,∴OB=OD=6.
∵AE=CF,OA=OC,∴OE=OF.
∵AE=EF-CF,∴AE+CF=EF,
∴2AE=EF=2OE,∴AE=OE.
又∵G是AB的中点,∴EG是△ABO的中位线,
∴EG=OB=3.
23.【解析】(1)证明:连接AC,如图1所示.
∵四边形ABCD是平行四边形,E,O,F分别是对角线BD上的四等分点,
∴AC一定经过点O,∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点.
∵G是AD的中点,∴GF为△AOD的中位线,
∴GF∥OA,GF=OA.
同理可得EH∥OC,EH=OC,∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形.
(2)当 ABCD满足AB⊥BD条件时,四边形GEHF是菱形.理由如下:
连接GH,如图2,则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH.
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形.
(3)①四边形GEHF是矩形.
理由:由(2)得四边形ABHG是平行四边形,
∴GH=AB.
∵BD=2AB,∴AB=BD=EF,∴GH=EF,
∴四边形GEHF是矩形.
②如图3,作AM⊥BD于点M,GN⊥BD于点N,则AM∥GN.
∵G是AD的中点,∴GN是△ADM的中位线,
∴GN=AM.
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=AB=1,AM=BM=,∴GN=.
∵BD=2AB=4,∴EF=BD=2,
∴△EFG的面积=EF·GN=×2×=,
∴四边形GEHF的面积=2△EFG的面积=.
2
