2023-2024学年初中数学人教版八年级下册第十六章 二次根式 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册第十六章 二次根式 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 71.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:02:06 | ||
图片预览



文档简介
第十六章 二次根式
(建议用时:90分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.在式子,,中,二次根式有( )
A.3个 B.2个 C.1个 D.0个
2.若无意义,则a的值可以是( )
A.0 B.-1 C.4 D.6
3.下列化简结果正确的是( )
A.-=-8 B.=±8 C.=-64 D.±=8
4.下列各式中,与的乘积是有理数的是( )
A. B. C. D.
5.下列选项中,计算正确的是( )
A.3+2=5 B.-=9 C.×= D.+=4
6.若x=,y=2+,则x与y的关系正确的是( )
A.xy=1 B.x>y C.x7.若最简二次根式与的被开方数相同,则m的值为( )
A. B.- C.1 D.-1
8.我们把形如a+b(a,b为有理数,为最简二次根式)的数叫做型无理数,如3+1是型无理数,则(-)2是( )
A.型无理数 B.型无理数 C.型无理数 D.(-)型无理数
9.若x=3-,则代数式x2-6x+9的值为( )
A.2026 B.-2026 C.2008 D.-2008
10.把四张形状、大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为 cm,宽为4 cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A.4 cm B.16 cm C.2(+4)cm D.4(-4)cm
二、填空题(本大题共6小题,每小题3分,满分18分)
11.当代数式有意义时,x应满足的条件是_______.
12.如图,这是一个简单的数值运算程序,当输入x的值为时,则输出y的值为________.
输入x×+输出y
13.计算:+|-2|=________.
14.已知=n,则+=________.(用含n的代数式表示)
15.我们定义[a]为不超过a的最大整数.例如:[3.14]=3,[8]=8,[-0.618]=-1,[-7.1]=-8,[-4]=-4.若[5-3]=-2,则a的取值范围是________.
16.【2023春·保定期末】嘉淇想通过“由特殊到一般”的方法探究下面二次根式的运算规律,下面是他的探究过程,请补充完整.
(1)具体运算,发现规律.
式子1:==.
式子2:===2.
式子3:===3.
式子4:________.
(2)观察、归纳,得出猜想.若n为正整数,则式子n为________.
三、解答题(本大题共10小题,满分72分)
17.(6分)计算:(1)--+.
(2)(+)×2.
18.(6分)计算:(1)(+)×(-)+-.
(2)(3-)2+÷.
19.(6分)实数a,b在数轴上的位置如图所示,化简:-.
20.(6分)已知+2=b+8.
(1)求a的值.
(2)求式子a2-b2的平方根.
21.(6分)已知a=+1,求代数式-的值.
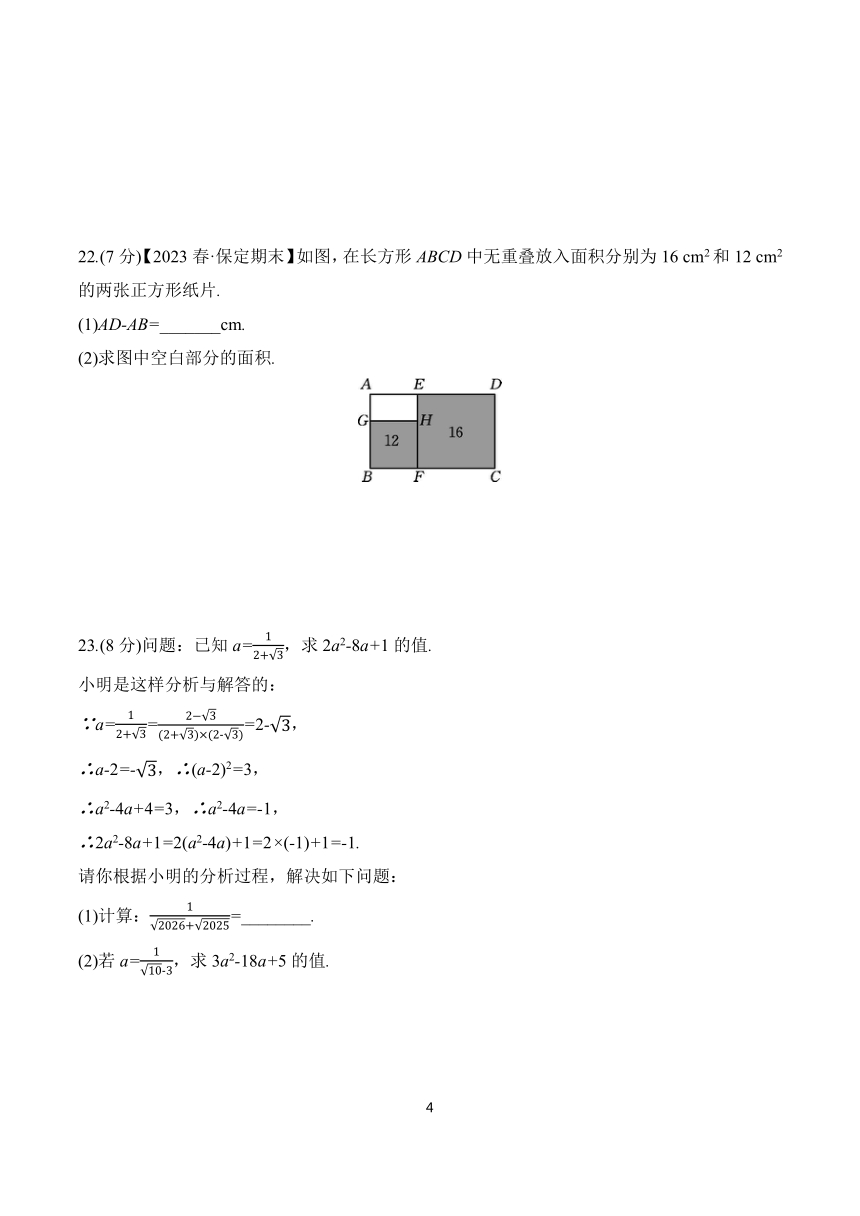
22.(7分)【2023春·保定期末】如图,在长方形ABCD中无重叠放入面积分别为16 cm2和12 cm2的两张正方形纸片.
(1)AD-AB=_______cm.
(2)求图中空白部分的面积.
23.(8分)问题:已知a=,求2a2-8a+1的值.
小明是这样分析与解答的:
∵a===2-,
∴a-2=-,∴(a-2)2=3,
∴a2-4a+4=3,∴a2-4a=-1,
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)计算:=________.
(2)若a=,求3a2-18a+5的值.
24.(8分)先在实数范围内化简,再求值:+,其中实数a,b满足a2+a2b2-4ab+b2+1=0.
25.(9分)已知M=+,N=,甲、乙两个同学在y=++1的条件下分别计算了M和N的值,甲得到的结论是M的值比N的值大,乙得到的结论是N的值比M的值大,请你解答下列问题:
(1)求x,y的值.
(2)判断谁的结论是正确的,并说明理由.
26.(10分)观察下列各式及其变形过程:a1==1-,a2==-,a3==-,….
(1)按照此规律和格式,请你写出第五个等式的变形过程:a5==________.
(2)请通过计算验证(1)中a5变形过程的正确性.
(3)按照此规律,计算:(a1+a2+a3+…+an)(a1-a2-a3-…-an+).
参考答案
1.C 2.B 3.A 4.A 5.C 6.D 7.C 8.A 9.A
10.B 11.x<4 12.5 13.2+ 14.n
15.316.(1)=4或===4
(2)=n
17.【解析】(1)原式=2---=-+.
(2)原式=(2+)×2
=4+2
=8+6.
18.【解析】(1)原式=3-2+4-2=1+2.
(2)原式=9-6+2+=11-6+2=11-4.
19.【解析】由图可得10,a-b<0,
故原式=b-1+a-b=a-1.
20.【解析】(1)由题意知解得a=17.
(2)由(1)可知a=17,则b+8=0,解得b=-8,
故a2-b2=172-(-8)2=225,
则a2-b2的平方根为±=±15.
21.【解析】原式=-=-=,
当a=+1时,原式==.
22.【解析】(1)2.
提示:∵两张正方形纸片的面积分别为16 cm2和12 cm2,
∴它们的边长分别为=4(cm),=2(cm),
∴AD-AB=(4+2)-4=2(cm).
(2)∴AG=EH=(4-2)cm,
∴空白部分的面积=AE×AG=2×(4-2)=(8-12)cm2.
23.【解析】(1)-.
(2)∵a===+3,
∴a-3=,∴(a-3)2=10,
∴a2-6a+9=10,∴a2-6a=1,
∴3a2-18a+5=3(a2-6a)+5=3×1+5=8.
24.【解析】原式=+=++2-=3.
∵a2+a2b2-4ab+b2+1=0,∴a2-2ab+b2+a2b2-2ab+1=0,∴(a-b)2+(ab-1)2=0,∴a-b=0,ab-1=0,
解得a=b,ab=1.
由+可知a和b都是正数,
∴a=b=1,∴原式=3×=3.
25.【解析】(1)∵y=++1,
∴解得x=4,∴y=1.
(2)甲的结论正确.
理由:M=+==+.
当x=4,y=1时,M=+=2+1=3.
N====.
∵3>,∴甲的结论正确.
26.【解析】(1)-.
(2)a5=====-.
(3)原式=1-+-+…+-1--+-…-++
=1-1+=1-=.
2
(建议用时:90分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.在式子,,中,二次根式有( )
A.3个 B.2个 C.1个 D.0个
2.若无意义,则a的值可以是( )
A.0 B.-1 C.4 D.6
3.下列化简结果正确的是( )
A.-=-8 B.=±8 C.=-64 D.±=8
4.下列各式中,与的乘积是有理数的是( )
A. B. C. D.
5.下列选项中,计算正确的是( )
A.3+2=5 B.-=9 C.×= D.+=4
6.若x=,y=2+,则x与y的关系正确的是( )
A.xy=1 B.x>y C.x
A. B.- C.1 D.-1
8.我们把形如a+b(a,b为有理数,为最简二次根式)的数叫做型无理数,如3+1是型无理数,则(-)2是( )
A.型无理数 B.型无理数 C.型无理数 D.(-)型无理数
9.若x=3-,则代数式x2-6x+9的值为( )
A.2026 B.-2026 C.2008 D.-2008
10.把四张形状、大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为 cm,宽为4 cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A.4 cm B.16 cm C.2(+4)cm D.4(-4)cm
二、填空题(本大题共6小题,每小题3分,满分18分)
11.当代数式有意义时,x应满足的条件是_______.
12.如图,这是一个简单的数值运算程序,当输入x的值为时,则输出y的值为________.
输入x×+输出y
13.计算:+|-2|=________.
14.已知=n,则+=________.(用含n的代数式表示)
15.我们定义[a]为不超过a的最大整数.例如:[3.14]=3,[8]=8,[-0.618]=-1,[-7.1]=-8,[-4]=-4.若[5-3]=-2,则a的取值范围是________.
16.【2023春·保定期末】嘉淇想通过“由特殊到一般”的方法探究下面二次根式的运算规律,下面是他的探究过程,请补充完整.
(1)具体运算,发现规律.
式子1:==.
式子2:===2.
式子3:===3.
式子4:________.
(2)观察、归纳,得出猜想.若n为正整数,则式子n为________.
三、解答题(本大题共10小题,满分72分)
17.(6分)计算:(1)--+.
(2)(+)×2.
18.(6分)计算:(1)(+)×(-)+-.
(2)(3-)2+÷.
19.(6分)实数a,b在数轴上的位置如图所示,化简:-.
20.(6分)已知+2=b+8.
(1)求a的值.
(2)求式子a2-b2的平方根.
21.(6分)已知a=+1,求代数式-的值.
22.(7分)【2023春·保定期末】如图,在长方形ABCD中无重叠放入面积分别为16 cm2和12 cm2的两张正方形纸片.
(1)AD-AB=_______cm.
(2)求图中空白部分的面积.
23.(8分)问题:已知a=,求2a2-8a+1的值.
小明是这样分析与解答的:
∵a===2-,
∴a-2=-,∴(a-2)2=3,
∴a2-4a+4=3,∴a2-4a=-1,
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)计算:=________.
(2)若a=,求3a2-18a+5的值.
24.(8分)先在实数范围内化简,再求值:+,其中实数a,b满足a2+a2b2-4ab+b2+1=0.
25.(9分)已知M=+,N=,甲、乙两个同学在y=++1的条件下分别计算了M和N的值,甲得到的结论是M的值比N的值大,乙得到的结论是N的值比M的值大,请你解答下列问题:
(1)求x,y的值.
(2)判断谁的结论是正确的,并说明理由.
26.(10分)观察下列各式及其变形过程:a1==1-,a2==-,a3==-,….
(1)按照此规律和格式,请你写出第五个等式的变形过程:a5==________.
(2)请通过计算验证(1)中a5变形过程的正确性.
(3)按照此规律,计算:(a1+a2+a3+…+an)(a1-a2-a3-…-an+).
参考答案
1.C 2.B 3.A 4.A 5.C 6.D 7.C 8.A 9.A
10.B 11.x<4 12.5 13.2+ 14.n
15.3
(2)=n
17.【解析】(1)原式=2---=-+.
(2)原式=(2+)×2
=4+2
=8+6.
18.【解析】(1)原式=3-2+4-2=1+2.
(2)原式=9-6+2+=11-6+2=11-4.
19.【解析】由图可得1
故原式=b-1+a-b=a-1.
20.【解析】(1)由题意知解得a=17.
(2)由(1)可知a=17,则b+8=0,解得b=-8,
故a2-b2=172-(-8)2=225,
则a2-b2的平方根为±=±15.
21.【解析】原式=-=-=,
当a=+1时,原式==.
22.【解析】(1)2.
提示:∵两张正方形纸片的面积分别为16 cm2和12 cm2,
∴它们的边长分别为=4(cm),=2(cm),
∴AD-AB=(4+2)-4=2(cm).
(2)∴AG=EH=(4-2)cm,
∴空白部分的面积=AE×AG=2×(4-2)=(8-12)cm2.
23.【解析】(1)-.
(2)∵a===+3,
∴a-3=,∴(a-3)2=10,
∴a2-6a+9=10,∴a2-6a=1,
∴3a2-18a+5=3(a2-6a)+5=3×1+5=8.
24.【解析】原式=+=++2-=3.
∵a2+a2b2-4ab+b2+1=0,∴a2-2ab+b2+a2b2-2ab+1=0,∴(a-b)2+(ab-1)2=0,∴a-b=0,ab-1=0,
解得a=b,ab=1.
由+可知a和b都是正数,
∴a=b=1,∴原式=3×=3.
25.【解析】(1)∵y=++1,
∴解得x=4,∴y=1.
(2)甲的结论正确.
理由:M=+==+.
当x=4,y=1时,M=+=2+1=3.
N====.
∵3>,∴甲的结论正确.
26.【解析】(1)-.
(2)a5=====-.
(3)原式=1-+-+…+-1--+-…-++
=1-1+=1-=.
2
