2023-2024学年初中数学人教版八年级下册17.1.1 勾股定理 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.1.1 勾股定理 课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:05:45 | ||
图片预览


文档简介
17.1.1 勾股定理
【练基础】
必备知识1 勾股定理
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+AB2=BC2 B.AB+BC=AC C.AC2-BC2=AB2 D.AC2+BC2=AB2
2.【邯郸期末】已知一个直角三角形的斜边长为15,一条直角边长为12,则另一条直角边长为( )
A.3 B.3 C.27 D.9
3.如图,这是一个围棋棋盘的局部,若棋盘是由边长均为1的小正方形组成的,则黑、白两棋子间的距离为_______.
4.若一个直角三角形的一条直角边长为7,其斜边长比另一条直角边长多1,则该直角三角形的斜边长为_______.
5.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若a=3,b=4,求c的值.
(2)若a=10,∠B=60°,求b,c的值.
必备知识2 勾股定理的验证
6.课堂上,王老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出两种图形,能证明勾股定理的是( )
A.①行,②不行 B.①不行,②行 C.①②都行 D.①②都不行
必备知识3 勾股定理的简单应用
7.【唐山路北区期中】等腰三角形的腰长为13,底边长为10,则它底边上的高为( )
A.12 B.7 C.6 D.5
8.【教材P26T2变式】【洛阳期中】已知平面直角坐标系内两点P(1,2),Q(2,-3),那么线段PQ的长等于( )
A.5 B. C. D.2
9.如图,这是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
10.如图,数轴上的点A表示的数是-2,点B表示的数是1,CB⊥AB于点B,且BC=2,以A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A. B.+2 C.-2 D.2
11.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连接PC.
(1)线段PC的最小值是_______.
(2)当PC=5时,AP的长是_______.
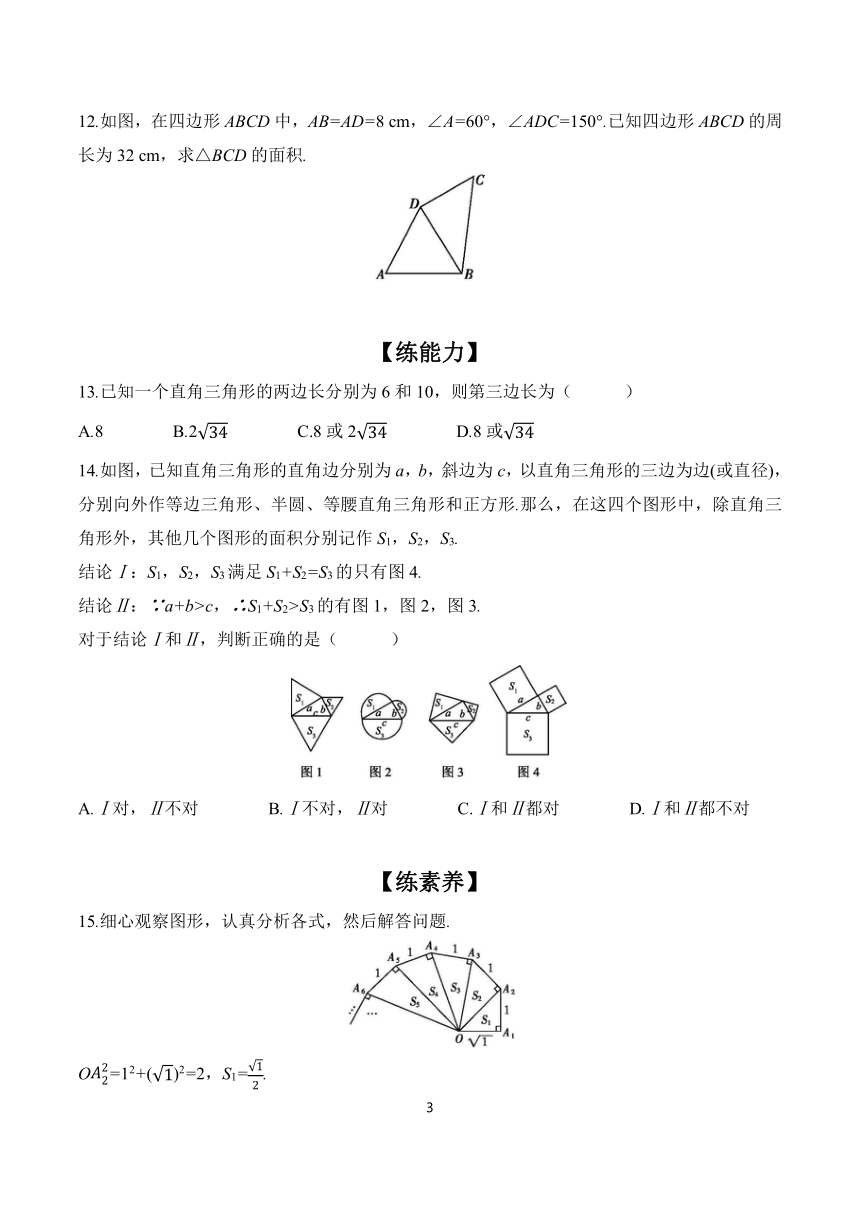
12.如图,在四边形ABCD中,AB=AD=8 cm,∠A=60°,∠ADC=150°.已知四边形ABCD的周长为32 cm,求△BCD的面积.
【练能力】
13.已知一个直角三角形的两边长分别为6和10,则第三边长为( )
A.8 B.2 C.8或2 D.8或
14.如图,已知直角三角形的直角边分别为a,b,斜边为c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,在这四个图形中,除直角三角形外,其他几个图形的面积分别记作S1,S2,S3.
结论Ⅰ:S1,S2,S3满足S1+S2=S3的只有图4.
结论Ⅱ:∵a+b>c,∴S1+S2>S3的有图1,图2,图3.
对于结论Ⅰ和Ⅱ,判断正确的是( )
A.Ⅰ对,Ⅱ不对 B.Ⅰ不对,Ⅱ对 C.Ⅰ和Ⅱ都对 D.Ⅰ和Ⅱ都不对
【练素养】
15.细心观察图形,认真分析各式,然后解答问题.
O=12+()2=2,S1=.
O=12+()2=3,S2=.
O=12+()2=4,S3=.
……
(1)OA10=________.
(2)若Sa=,则a的值为_______.
(3)用含n(n是正整数)的等式表示上述变化规律.
(4)求+++…+的值.
参考答案
【练基础】
1.D 2.D 3.5
4.25 【解析】设该直角三角形的斜边长为x,则另一条直角边长为x-1.
由勾股定理,得x2=72+(x-1)2,解得x=25,
∴该直角三角形的斜边长为25.
5.【解析】(1)∵在Rt△ABC中,∠C=90°,a=3,b=4,
∴c==5.
(2)∵在Rt△ABC中,∠C=90°,∠B=60°,∴∠A=30°.
∵a=10,∴c=20,b==10.
6.A 7.A 8.B 9.A 10.C
11.(1)4.8 (2)5或2.2
【解析】(1)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10,由垂线段最短,得当PC⊥AB时,PC的值最小,此时△ABC的面积=AB·PC=AC·BC,
∴AB·PC=AC·BC,∴PC===4.8.
(2)如图,过点C作CQ⊥AB于点Q,由(1)得CQ=4.8,由勾股定理得AQ==3.6,PQ==1.4.
当点 P在线段BQ上时,AP=AQ+PQ=3.6+1.4=5;
当点P在线段AQ上时,AP=AQ-PQ=3.6-1.4=2.2.
综上所述,AP的长是5或2.2.
12.【解析】∵AB=AD=8 cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,∴∠CDB=150°-60°=90°,∴△BCD是直角三角形.
∵四边形ABCD的周长为32 cm,∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=x,则BC=16-x.由勾股定理得82+x2=(16-x)2,解得x=6,
∴S△BCD=×6×8=24(cm2).
【练能力】
13.C 14.D
【练素养】
15.【解析】(1).(2)20.(3)O=n,Sn=.
(4)+++…+=++++…+=.
2
【练基础】
必备知识1 勾股定理
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+AB2=BC2 B.AB+BC=AC C.AC2-BC2=AB2 D.AC2+BC2=AB2
2.【邯郸期末】已知一个直角三角形的斜边长为15,一条直角边长为12,则另一条直角边长为( )
A.3 B.3 C.27 D.9
3.如图,这是一个围棋棋盘的局部,若棋盘是由边长均为1的小正方形组成的,则黑、白两棋子间的距离为_______.
4.若一个直角三角形的一条直角边长为7,其斜边长比另一条直角边长多1,则该直角三角形的斜边长为_______.
5.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若a=3,b=4,求c的值.
(2)若a=10,∠B=60°,求b,c的值.
必备知识2 勾股定理的验证
6.课堂上,王老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出两种图形,能证明勾股定理的是( )
A.①行,②不行 B.①不行,②行 C.①②都行 D.①②都不行
必备知识3 勾股定理的简单应用
7.【唐山路北区期中】等腰三角形的腰长为13,底边长为10,则它底边上的高为( )
A.12 B.7 C.6 D.5
8.【教材P26T2变式】【洛阳期中】已知平面直角坐标系内两点P(1,2),Q(2,-3),那么线段PQ的长等于( )
A.5 B. C. D.2
9.如图,这是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
10.如图,数轴上的点A表示的数是-2,点B表示的数是1,CB⊥AB于点B,且BC=2,以A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A. B.+2 C.-2 D.2
11.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连接PC.
(1)线段PC的最小值是_______.
(2)当PC=5时,AP的长是_______.
12.如图,在四边形ABCD中,AB=AD=8 cm,∠A=60°,∠ADC=150°.已知四边形ABCD的周长为32 cm,求△BCD的面积.
【练能力】
13.已知一个直角三角形的两边长分别为6和10,则第三边长为( )
A.8 B.2 C.8或2 D.8或
14.如图,已知直角三角形的直角边分别为a,b,斜边为c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,在这四个图形中,除直角三角形外,其他几个图形的面积分别记作S1,S2,S3.
结论Ⅰ:S1,S2,S3满足S1+S2=S3的只有图4.
结论Ⅱ:∵a+b>c,∴S1+S2>S3的有图1,图2,图3.
对于结论Ⅰ和Ⅱ,判断正确的是( )
A.Ⅰ对,Ⅱ不对 B.Ⅰ不对,Ⅱ对 C.Ⅰ和Ⅱ都对 D.Ⅰ和Ⅱ都不对
【练素养】
15.细心观察图形,认真分析各式,然后解答问题.
O=12+()2=2,S1=.
O=12+()2=3,S2=.
O=12+()2=4,S3=.
……
(1)OA10=________.
(2)若Sa=,则a的值为_______.
(3)用含n(n是正整数)的等式表示上述变化规律.
(4)求+++…+的值.
参考答案
【练基础】
1.D 2.D 3.5
4.25 【解析】设该直角三角形的斜边长为x,则另一条直角边长为x-1.
由勾股定理,得x2=72+(x-1)2,解得x=25,
∴该直角三角形的斜边长为25.
5.【解析】(1)∵在Rt△ABC中,∠C=90°,a=3,b=4,
∴c==5.
(2)∵在Rt△ABC中,∠C=90°,∠B=60°,∴∠A=30°.
∵a=10,∴c=20,b==10.
6.A 7.A 8.B 9.A 10.C
11.(1)4.8 (2)5或2.2
【解析】(1)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10,由垂线段最短,得当PC⊥AB时,PC的值最小,此时△ABC的面积=AB·PC=AC·BC,
∴AB·PC=AC·BC,∴PC===4.8.
(2)如图,过点C作CQ⊥AB于点Q,由(1)得CQ=4.8,由勾股定理得AQ==3.6,PQ==1.4.
当点 P在线段BQ上时,AP=AQ+PQ=3.6+1.4=5;
当点P在线段AQ上时,AP=AQ-PQ=3.6-1.4=2.2.
综上所述,AP的长是5或2.2.
12.【解析】∵AB=AD=8 cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,∴∠CDB=150°-60°=90°,∴△BCD是直角三角形.
∵四边形ABCD的周长为32 cm,∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=x,则BC=16-x.由勾股定理得82+x2=(16-x)2,解得x=6,
∴S△BCD=×6×8=24(cm2).
【练能力】
13.C 14.D
【练素养】
15.【解析】(1).(2)20.(3)O=n,Sn=.
(4)+++…+=++++…+=.
2
