2023-2024学年初中数学人教版八年级下册17.1.2 勾股定理的应用 课时练习 (含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.1.2 勾股定理的应用 课时练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 188.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:06:21 | ||
图片预览

文档简介
17.1.2 勾股定理的应用
【练基础】
必备知识 勾股定理的应用
1.如图,一竖直的木杆在离地面3米处折断,木杆顶端落在地面离木杆底端4米处,则木杆折断之前的高度为( )
A.7米 B.8米 C.9米 D.12米
2.【教材P33例2变式】如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距40 nmile.客轮以60 nmile/h的速度沿北偏西60°方向航行0.5 h到达B处,此时客轮距离灯塔A( )
A.30 nmile B.40 nmile C.50 nmile D.60 nmile
3.《九章算术》中有这样一道题:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何 大意:今有一竖直着的木柱(如图所示),在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有3尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8尺)处时而绳索用尽,求木桩AB的长度.木柱AB的长为( )
A.尺 B.尺 C.尺 D.尺
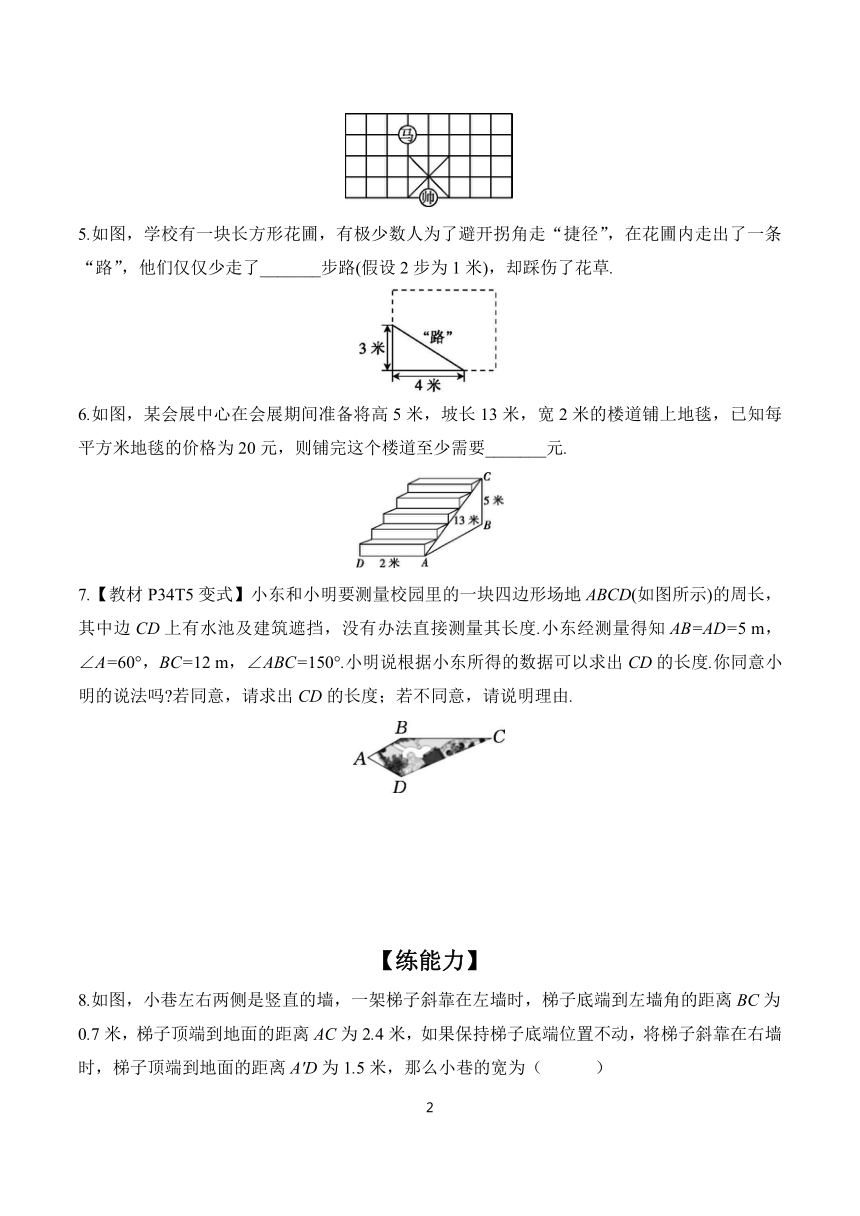
4.在如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为_______.
5.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了_______步路(假设2步为1米),却踩伤了花草.
6.如图,某会展中心在会展期间准备将高5米,坡长13米,宽2米的楼道铺上地毯,已知每平方米地毯的价格为20元,则铺完这个楼道至少需要_______元.
7.【教材P34T5变式】小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池及建筑遮挡,没有办法直接测量其长度.小东经测量得知AB=AD=5 m,∠A=60°,BC=12 m,∠ABC=150°.小明说根据小东所得的数据可以求出CD的长度.你同意小明的说法吗 若同意,请求出CD的长度;若不同意,请说明理由.
【练能力】
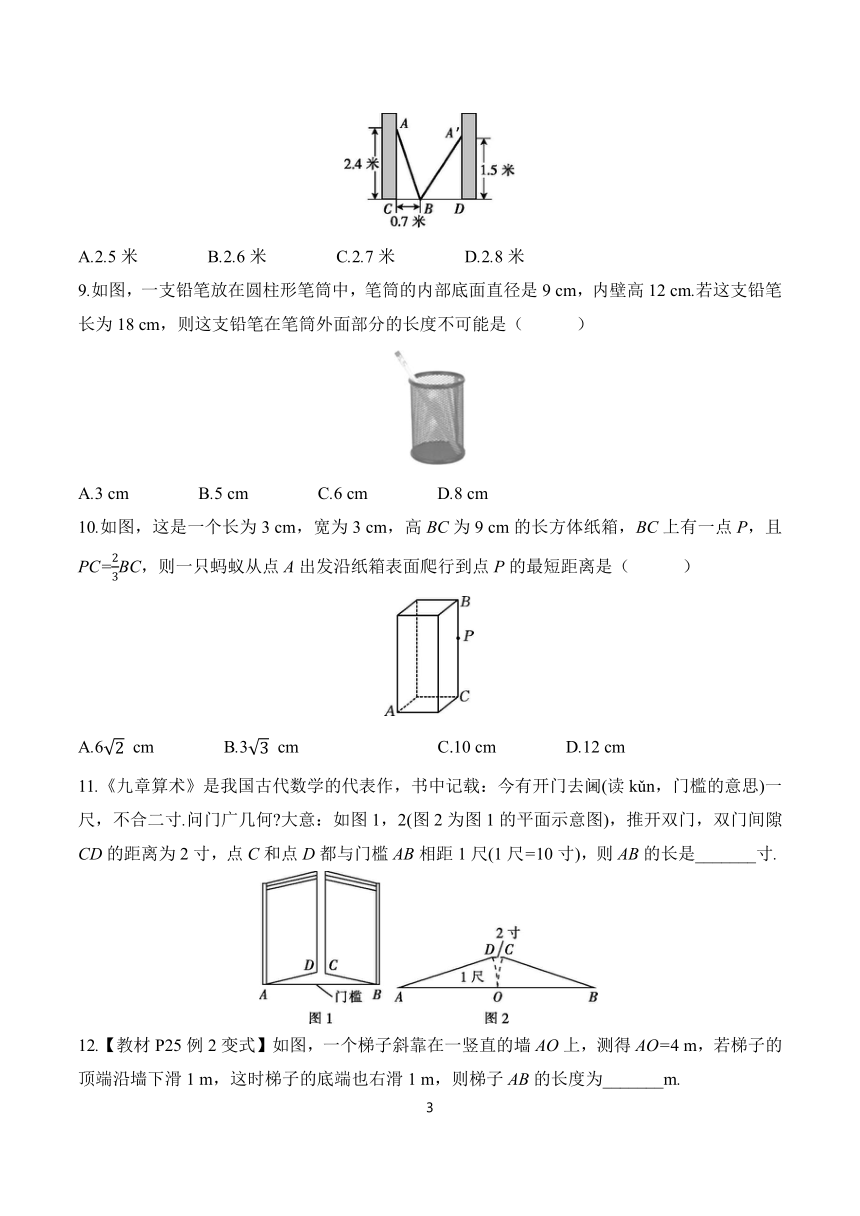
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,那么小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
9.如图,一支铅笔放在圆柱形笔筒中,笔筒的内部底面直径是9 cm,内壁高12 cm.若这支铅笔长为18 cm,则这支铅笔在笔筒外面部分的长度不可能是( )
A.3 cm B.5 cm C.6 cm D.8 cm
10.如图,这是一个长为3 cm,宽为3 cm,高BC为9 cm的长方体纸箱,BC上有一点P,且PC=BC,则一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是( )
A.6 cm B.3 cm C.10 cm D.12 cm
11.《九章算术》是我国古代数学的代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸.问门广几何 大意:如图1,2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D都与门槛AB相距1尺(1尺=10寸),则AB的长是_______寸.
12.【教材P25例2变式】如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4 m,若梯子的顶端沿墙下滑1 m,这时梯子的底端也右滑1 m,则梯子AB的长度为_______m.
13.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位: km).笔直铁路经过A,B两地.
(1)A,B间的距离为_______ km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为_______ km.
【练素养】
14.小王与小林进行遥控赛车游戏,终点为点A,小王的赛车从点C出发,以4米/秒的速度由西向东行驶,同时小林的赛车从点B出发,以3米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于25米时,遥控信号会相互干扰,AC=40米,AB=30米.
(1)当出发3秒时,遥控信号是否会相互干扰
(2)当两赛车距A点的距离之和为35米时,遥控信号是否会相互干扰
参考答案
【练基础】
1.B 2.C 3.B 4. 5.4 6.680
7.【解析】同意小明的说法.
如图,连接BD.
∵AB=AD=5 m,∠A=60°,
∴△ABD是等边三角形,
∴BD=5 m,∠ABD=60°.
∵∠ABC=150°,∴∠DBC=90°.
∵BC=12 m,BD=5 m,∴CD==13(m).
答:CD的长度为13 m.
【练能力】
8.C 9.D
10.A 【解析】连接AP.由题意知PC=6 cm,
(1)如图1,AD=3 cm,DP=3+6=9(cm),在Rt△ADP中,AP==3(cm);
(2)如图2,
CP=6 cm,AC=3+3=6(cm),在Rt△ACP中,AP==6(cm).
∵3>6,
∴蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是6 cm.
11.101 12.5
13.(1)20 (2)13
【解析】(1)∵A(12,1),B(-8,1),∴AB∥x轴,∴AB=12-(-8)=20.
(2)
如图,设AB与y轴交于点E,则CE⊥AB,故CE为从C到AB的最短公路l.连接AC,作AC的垂直平分线,交l于点D,交AC于点F.由垂直平分线的性质可知DA=DC,即点D到A,C的距离相等.
∵E(0,1),C(0,-17),A(12,1),∴CE=1-(-17)=18,AE=12.设DA=DC=a,则ED=18-a.
在Rt△ADE中,根据勾股定理,得ED2+AE2=DA2,即(18-a)2+122=a2,解得a=13,即DC=13.
【练素养】
14.【解析】(1)如图,当出发3秒时,CC1=12米,BB1=9米.
∵AC=40米,AB=30米,
∴AC1=28米,AB1=21米,
∴B1=282+212>252,
∴当出发3秒时,遥控信号不会相互干扰.
(2)如图,设出发t秒时,两赛车距A点的距离之和为35米,
根据题意,得40-4t+30-3t=35,解得t=5,
此时A+A=202+152=252,
∴C2B2=25米,
∴当两赛车距A点的距离之和为35米时,遥控信号会相互干扰.
2
【练基础】
必备知识 勾股定理的应用
1.如图,一竖直的木杆在离地面3米处折断,木杆顶端落在地面离木杆底端4米处,则木杆折断之前的高度为( )
A.7米 B.8米 C.9米 D.12米
2.【教材P33例2变式】如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距40 nmile.客轮以60 nmile/h的速度沿北偏西60°方向航行0.5 h到达B处,此时客轮距离灯塔A( )
A.30 nmile B.40 nmile C.50 nmile D.60 nmile
3.《九章算术》中有这样一道题:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何 大意:今有一竖直着的木柱(如图所示),在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有3尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8尺)处时而绳索用尽,求木桩AB的长度.木柱AB的长为( )
A.尺 B.尺 C.尺 D.尺
4.在如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为_______.
5.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了_______步路(假设2步为1米),却踩伤了花草.
6.如图,某会展中心在会展期间准备将高5米,坡长13米,宽2米的楼道铺上地毯,已知每平方米地毯的价格为20元,则铺完这个楼道至少需要_______元.
7.【教材P34T5变式】小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池及建筑遮挡,没有办法直接测量其长度.小东经测量得知AB=AD=5 m,∠A=60°,BC=12 m,∠ABC=150°.小明说根据小东所得的数据可以求出CD的长度.你同意小明的说法吗 若同意,请求出CD的长度;若不同意,请说明理由.
【练能力】
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,那么小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
9.如图,一支铅笔放在圆柱形笔筒中,笔筒的内部底面直径是9 cm,内壁高12 cm.若这支铅笔长为18 cm,则这支铅笔在笔筒外面部分的长度不可能是( )
A.3 cm B.5 cm C.6 cm D.8 cm
10.如图,这是一个长为3 cm,宽为3 cm,高BC为9 cm的长方体纸箱,BC上有一点P,且PC=BC,则一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是( )
A.6 cm B.3 cm C.10 cm D.12 cm
11.《九章算术》是我国古代数学的代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸.问门广几何 大意:如图1,2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D都与门槛AB相距1尺(1尺=10寸),则AB的长是_______寸.
12.【教材P25例2变式】如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4 m,若梯子的顶端沿墙下滑1 m,这时梯子的底端也右滑1 m,则梯子AB的长度为_______m.
13.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位: km).笔直铁路经过A,B两地.
(1)A,B间的距离为_______ km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为_______ km.
【练素养】
14.小王与小林进行遥控赛车游戏,终点为点A,小王的赛车从点C出发,以4米/秒的速度由西向东行驶,同时小林的赛车从点B出发,以3米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于25米时,遥控信号会相互干扰,AC=40米,AB=30米.
(1)当出发3秒时,遥控信号是否会相互干扰
(2)当两赛车距A点的距离之和为35米时,遥控信号是否会相互干扰
参考答案
【练基础】
1.B 2.C 3.B 4. 5.4 6.680
7.【解析】同意小明的说法.
如图,连接BD.
∵AB=AD=5 m,∠A=60°,
∴△ABD是等边三角形,
∴BD=5 m,∠ABD=60°.
∵∠ABC=150°,∴∠DBC=90°.
∵BC=12 m,BD=5 m,∴CD==13(m).
答:CD的长度为13 m.
【练能力】
8.C 9.D
10.A 【解析】连接AP.由题意知PC=6 cm,
(1)如图1,AD=3 cm,DP=3+6=9(cm),在Rt△ADP中,AP==3(cm);
(2)如图2,
CP=6 cm,AC=3+3=6(cm),在Rt△ACP中,AP==6(cm).
∵3>6,
∴蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是6 cm.
11.101 12.5
13.(1)20 (2)13
【解析】(1)∵A(12,1),B(-8,1),∴AB∥x轴,∴AB=12-(-8)=20.
(2)
如图,设AB与y轴交于点E,则CE⊥AB,故CE为从C到AB的最短公路l.连接AC,作AC的垂直平分线,交l于点D,交AC于点F.由垂直平分线的性质可知DA=DC,即点D到A,C的距离相等.
∵E(0,1),C(0,-17),A(12,1),∴CE=1-(-17)=18,AE=12.设DA=DC=a,则ED=18-a.
在Rt△ADE中,根据勾股定理,得ED2+AE2=DA2,即(18-a)2+122=a2,解得a=13,即DC=13.
【练素养】
14.【解析】(1)如图,当出发3秒时,CC1=12米,BB1=9米.
∵AC=40米,AB=30米,
∴AC1=28米,AB1=21米,
∴B1=282+212>252,
∴当出发3秒时,遥控信号不会相互干扰.
(2)如图,设出发t秒时,两赛车距A点的距离之和为35米,
根据题意,得40-4t+30-3t=35,解得t=5,
此时A+A=202+152=252,
∴C2B2=25米,
∴当两赛车距A点的距离之和为35米时,遥控信号会相互干扰.
2
