2023-2024学年初中数学人教版八年级下册17.2.1 勾股定理的逆定理 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.2.1 勾股定理的逆定理 课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:07:30 | ||
图片预览

文档简介
17.2.1 勾股定理的逆定理
【练基础】
必备知识1 互逆命题与互逆定理
1.下列命题的逆命题是假命题的是( )
A.全等三角形的对应角相等
B.两直线平行,同位角相等
C.等边三角形三个角相等
D.直角三角形中,斜边的平方等于两直角边的平方和
2.下列选项中,可以用来说明“若a2>1,则a>1”是假命题的反例是( )
A.a=-3 B.a=-1 C.a=1 D.a=3
必备知识2 勾股定理的逆定理
3.【教材P34T1变式】下列各组数中,能作为直角三角形的三边长的是( )
A.1.5,2,3 B.2,3,4 C.1,1, D.5,13,14
4.五根小棒,其长度(单位: cm)分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
5.【石家庄期末】三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形是_______三角形.
6.【教材P38T5变式】【石家庄期中】若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是_______ cm2.
7.如图,在锐角三角形ABC中,AB=13,AC=15,点D是BC边上一点,BD=5,AD=12,求BC的长.
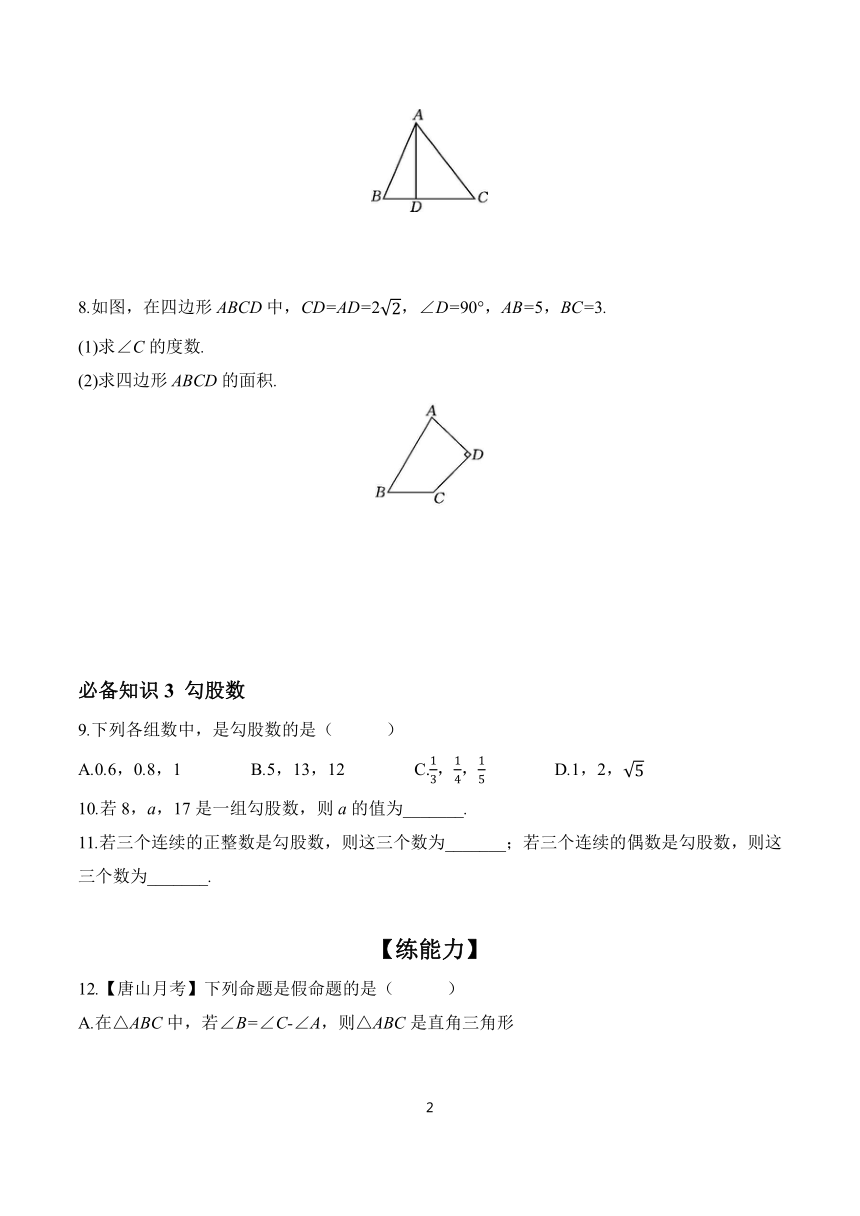
8.如图,在四边形ABCD中,CD=AD=2,∠D=90°,AB=5,BC=3.
(1)求∠C的度数.
(2)求四边形ABCD的面积.
必备知识3 勾股数
9.下列各组数中,是勾股数的是( )
A.0.6,0.8,1 B.5,13,12 C.,, D.1,2,
10.若8,a,17是一组勾股数,则a的值为_______.
11.若三个连续的正整数是勾股数,则这三个数为_______;若三个连续的偶数是勾股数,则这三个数为_______.
【练能力】
12.【唐山月考】下列命题是假命题的是( )
A.在△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形 C.在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
D.在△ABC中,若a∶b∶c=3∶4∶5,则△ABC是直角三角形
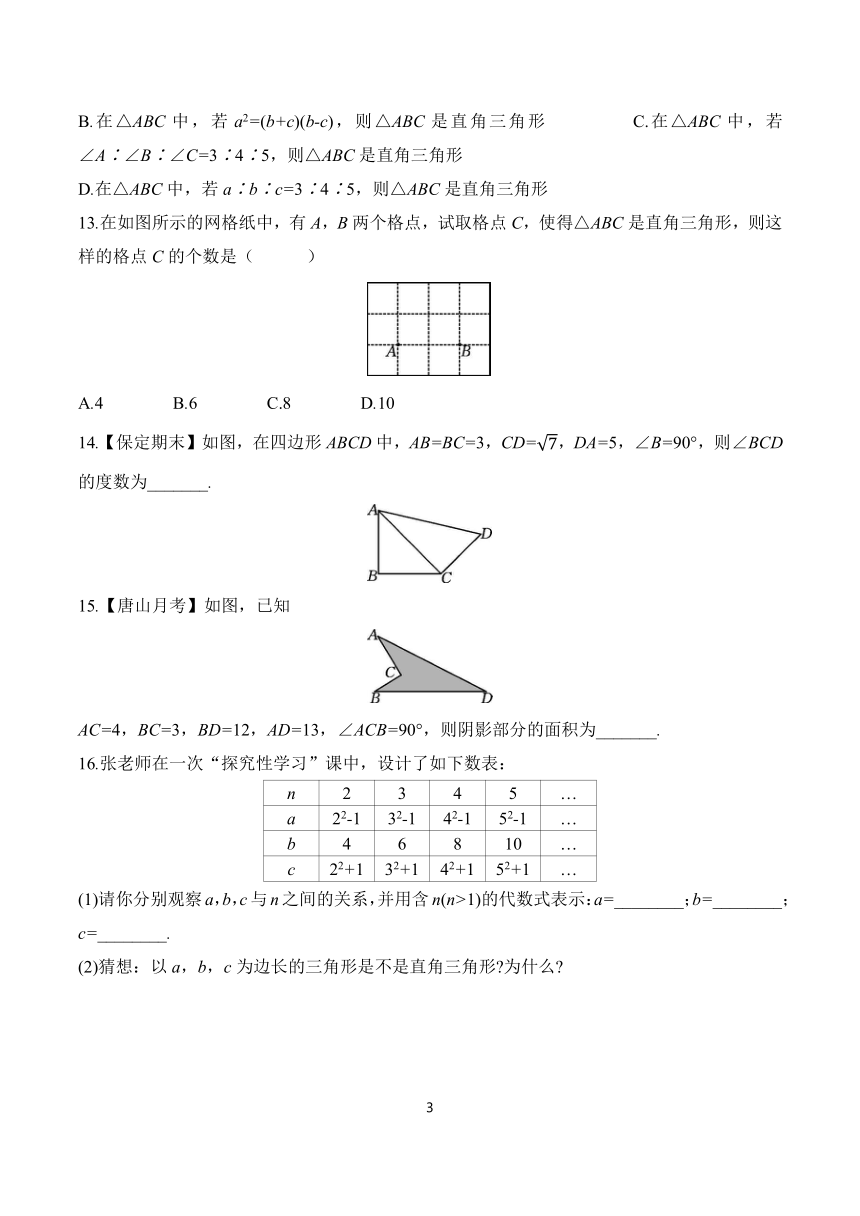
13.在如图所示的网格纸中,有A,B两个格点,试取格点C,使得△ABC是直角三角形,则这样的格点C的个数是( )
A.4 B.6 C.8 D.10
14.【保定期末】如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,则∠BCD的度数为_______.
15.【唐山月考】如图,已知
AC=4,BC=3,BD=12,AD=13,∠ACB=90°,则阴影部分的面积为_______.
16.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含n(n>1)的代数式表示:a=________;b=________;c=________.
(2)猜想:以a,b,c为边长的三角形是不是直角三角形 为什么
【练素养】
17.我们新定义一种三角形:两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗 _______.(填“是”或“不是”)
(2)若某三角形的三边长分别为1,,2,判断该三角形是不是奇异三角形,并说明理由.
(3)在Rt△ABC中,两边长分别为a,c,且a2=50,c2=100,请通过计算说明这个三角形是不是奇异三角形.
(4)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a2∶b2∶c2的值.
参考答案
【练基础】
1.A 2.A 3.C 4.C 5.直角 6.150
7.【解析】在△ABD中,AB=13,BD=5,AD=12,
∴BD2+AD2=52+122=169,AB2=132=169,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵D是BC边上一点,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,由勾股定理,得CD===9,
∴BC=BD+CD=5+9=14.
8.【解析】(1)如图,连接AC.
∵CD=AD=2,∠D=90°,
∴∠ACD=∠DAC=45°,AC==
=4.
∵AB=5,BC=3,∴AB2=AC2+BC2,
∴∠ACB=90°,∴∠BCD=90°+45°=135°.
(2)S四边形ABCD=S△ABC+S△ACD=×3×4+×2×2=6+4=10.
9.B 10.15 11.3,4,5;6,8,10
【练能力】
12.C
13.C 【解析】如图,这样的格点C有8个.
14.135° 15.24
16.【解析】(1)n2-1;2n;n2+1.
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,
∴a2+b2=c2,
∴以a,b,c为边长的三角形是直角三角形.
【练素养】
17.【解析】(1)是.
提示:设等边三角形的边长为a.
∵a2+a2=2a2,∴等边三角形一定是奇异三角形.
(2)是.理由:∵12+()2=2×22,∴该三角形是奇异三角形.
(3)当c为斜边时,b2=c2-a2=50,Rt△ABC不是奇异三角形;
当b为斜边时,b2=c2+a2=150.
∵50+150=2×100,∴a2+b2=2c2,
∴Rt△ABC是奇异三角形.
(4)在Rt△ABC中,∠C=90°,∴a2+b2=c2.
∵c>b>a,∴2c2>b2+a2,2a2∵Rt△ABC是奇异三角形,∴2b2=a2+c2,
∴2b2=a2+a2+b2,
∴b2=2a2,∴c2=3a2,∴a2∶b2∶c2=1∶2∶3.
2
【练基础】
必备知识1 互逆命题与互逆定理
1.下列命题的逆命题是假命题的是( )
A.全等三角形的对应角相等
B.两直线平行,同位角相等
C.等边三角形三个角相等
D.直角三角形中,斜边的平方等于两直角边的平方和
2.下列选项中,可以用来说明“若a2>1,则a>1”是假命题的反例是( )
A.a=-3 B.a=-1 C.a=1 D.a=3
必备知识2 勾股定理的逆定理
3.【教材P34T1变式】下列各组数中,能作为直角三角形的三边长的是( )
A.1.5,2,3 B.2,3,4 C.1,1, D.5,13,14
4.五根小棒,其长度(单位: cm)分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
5.【石家庄期末】三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形是_______三角形.
6.【教材P38T5变式】【石家庄期中】若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是_______ cm2.
7.如图,在锐角三角形ABC中,AB=13,AC=15,点D是BC边上一点,BD=5,AD=12,求BC的长.
8.如图,在四边形ABCD中,CD=AD=2,∠D=90°,AB=5,BC=3.
(1)求∠C的度数.
(2)求四边形ABCD的面积.
必备知识3 勾股数
9.下列各组数中,是勾股数的是( )
A.0.6,0.8,1 B.5,13,12 C.,, D.1,2,
10.若8,a,17是一组勾股数,则a的值为_______.
11.若三个连续的正整数是勾股数,则这三个数为_______;若三个连续的偶数是勾股数,则这三个数为_______.
【练能力】
12.【唐山月考】下列命题是假命题的是( )
A.在△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形 C.在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
D.在△ABC中,若a∶b∶c=3∶4∶5,则△ABC是直角三角形
13.在如图所示的网格纸中,有A,B两个格点,试取格点C,使得△ABC是直角三角形,则这样的格点C的个数是( )
A.4 B.6 C.8 D.10
14.【保定期末】如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,则∠BCD的度数为_______.
15.【唐山月考】如图,已知
AC=4,BC=3,BD=12,AD=13,∠ACB=90°,则阴影部分的面积为_______.
16.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含n(n>1)的代数式表示:a=________;b=________;c=________.
(2)猜想:以a,b,c为边长的三角形是不是直角三角形 为什么
【练素养】
17.我们新定义一种三角形:两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗 _______.(填“是”或“不是”)
(2)若某三角形的三边长分别为1,,2,判断该三角形是不是奇异三角形,并说明理由.
(3)在Rt△ABC中,两边长分别为a,c,且a2=50,c2=100,请通过计算说明这个三角形是不是奇异三角形.
(4)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a2∶b2∶c2的值.
参考答案
【练基础】
1.A 2.A 3.C 4.C 5.直角 6.150
7.【解析】在△ABD中,AB=13,BD=5,AD=12,
∴BD2+AD2=52+122=169,AB2=132=169,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵D是BC边上一点,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,由勾股定理,得CD===9,
∴BC=BD+CD=5+9=14.
8.【解析】(1)如图,连接AC.
∵CD=AD=2,∠D=90°,
∴∠ACD=∠DAC=45°,AC==
=4.
∵AB=5,BC=3,∴AB2=AC2+BC2,
∴∠ACB=90°,∴∠BCD=90°+45°=135°.
(2)S四边形ABCD=S△ABC+S△ACD=×3×4+×2×2=6+4=10.
9.B 10.15 11.3,4,5;6,8,10
【练能力】
12.C
13.C 【解析】如图,这样的格点C有8个.
14.135° 15.24
16.【解析】(1)n2-1;2n;n2+1.
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,
∴a2+b2=c2,
∴以a,b,c为边长的三角形是直角三角形.
【练素养】
17.【解析】(1)是.
提示:设等边三角形的边长为a.
∵a2+a2=2a2,∴等边三角形一定是奇异三角形.
(2)是.理由:∵12+()2=2×22,∴该三角形是奇异三角形.
(3)当c为斜边时,b2=c2-a2=50,Rt△ABC不是奇异三角形;
当b为斜边时,b2=c2+a2=150.
∵50+150=2×100,∴a2+b2=2c2,
∴Rt△ABC是奇异三角形.
(4)在Rt△ABC中,∠C=90°,∴a2+b2=c2.
∵c>b>a,∴2c2>b2+a2,2a2
∴2b2=a2+a2+b2,
∴b2=2a2,∴c2=3a2,∴a2∶b2∶c2=1∶2∶3.
2
