2023-2024学年初中数学人教版八年级下册17.2.2 勾股定理逆定理的应用 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.2.2 勾股定理逆定理的应用 课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:08:14 | ||
图片预览


文档简介
17.2.2 勾股定理逆定理的应用
【练基础】
必备知识1 勾股定理逆定理的应用
1.如图,这是一块四边形木板,其中AB=16 cm,BC=24 cm,CD=9 cm,AD=25 cm,∠B=∠C=90°.李师傅找到BC边的中点P,连接AP,DP,发现△APD是直角三角形,请通过计算说明理由.
2.如图,在一次数学实践活动课上,老师让甲、乙两名同学同时从操场上的同一地点O出发,分别沿一固定方向行走.甲的速度是每分钟16 m,乙的速度是每分钟12 m,步行5分钟后,两人分别到达A,B两点,此时测得AB=100 m,如果甲同学沿西北方向前行,请判断乙同学行走的方向,并说明理由.
3.某中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的平均步行速度为30 m/min,第二组的平均步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1500 m.
(1)请通过计算判断这两组同学行走的方向是否成直角.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇
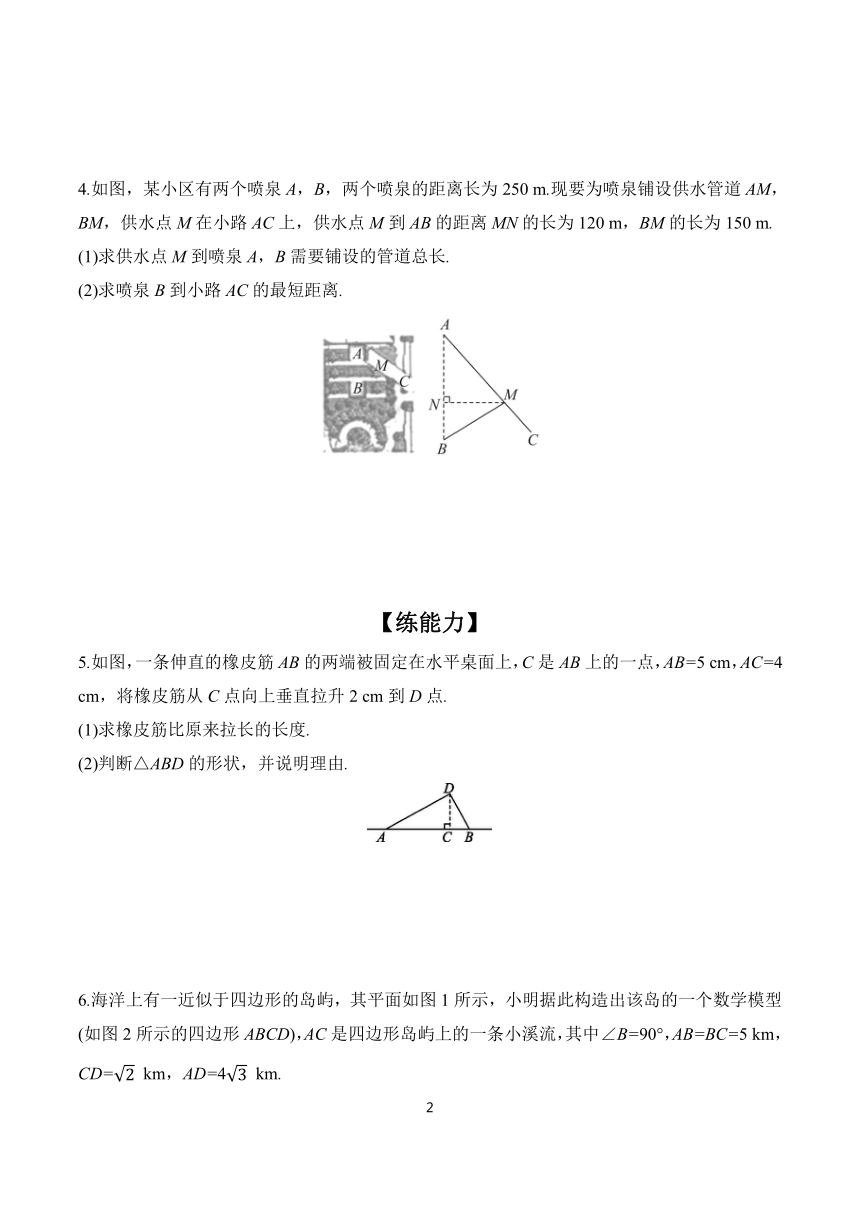
4.如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长.
(2)求喷泉B到小路AC的最短距离.
【练能力】
5.如图,一条伸直的橡皮筋AB的两端被固定在水平桌面上,C是AB上的一点,AB=5 cm,AC=4 cm,将橡皮筋从C点向上垂直拉升2 cm到D点.
(1)求橡皮筋比原来拉长的长度.
(2)判断△ABD的形状,并说明理由.
6.海洋上有一近似于四边形的岛屿,其平面如图1所示,小明据此构造出该岛的一个数学模型(如图2所示的四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5 km,CD= km,AD=4 km.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
【练素养】
7.如图,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A,D,B在同一条直线上),并新修一条路CD,测得CA=6.5千米,CD=6千米,AD=2.5千米.
(1)问CD是否为从村庄C到河边最近的路 请判断并说明理由.
(2)求原来的路BC的长.
参考答案
【练基础】
1.【解析】∵P为BC的中点,
∴BP=CP=BC=12(cm).
在Rt△ABP中,∠B=90°,根据勾股定理可得AP==20(cm).
在Rt△DCP中,同理可得DP=15(cm).
∵152+202=252,
∴AP2+DP2=AD2,
∴∠APD=90°,△APD是直角三角形.
2.【解析】乙同学行走的方向是东北方向.
理由:由题意可知OA=16×5=80(m),OB=12×5=60(m).
∵AB=100(m),
∴OA2+OB2=802+602=10000(m2),AB2=1002=10000(m2),
∴OA2+OB2=AB2,
∴∠AOB=90°.
由已知得∠AON=45°,∴∠BON=45°,
∴乙同学行走的方向是东北方向.
3.【解析】(1)半小时以后,第一组的路程:30×30=900(m).
第二组的路程:40×30=1200(m).
∵9002+12002=15002,
∴两组同学行走的方向成直角.
(2)设x min后两组同学相遇.
根据题意得30x+40x=1500,
解得x=(min).
答:经过 min后两组同学才能相遇.
4.【解析】(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
(2)∵AB=250 m,AM=200 m,BM=150 m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150 m.
【练能力】
5.【解析】(1)∵AB=5 cm,AC=4 cm,CD=2 cm,
在Rt△ACD中,
AD===2(cm),
在Rt△BCD中,
DB===(cm),
AD+DB-AB=2+-5=(3-5)(cm).
答:橡皮筋比原来拉伸了(3-5)cm.
(2)△ABD是直角三角形,
理由:∵AB2=52=25,AD2+DB2=(2)2+()2=20+5=25,
∴AB2=AD2+DB2,
∴△ABD是直角三角形.
6.【解析】(1)∵∠B=90°,AB=BC=5 km,
∴AC===5(km),
∴小溪流AC的长为5 km.
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,
则∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD
=×5×5+××4
=+2km2.
∴四边形ABCD的面积为+2km2.
【练素养】
7.【解析】(1)是.
理由:∵62+2.52=6.52,∴CD2+AD2=AC2,
∴∠ADC=90°,∴CD⊥AB,
∴CD是从村庄C到河边最近的路.
(2)设BC=x千米,则BD=(x-2.5)千米.
∵∠BDC=90°,∴CD2+BD2=BC2,即62+(x-2.5)2=x2,解得x=8.45.
答:原来的路BC的长为8.45千米.
2
【练基础】
必备知识1 勾股定理逆定理的应用
1.如图,这是一块四边形木板,其中AB=16 cm,BC=24 cm,CD=9 cm,AD=25 cm,∠B=∠C=90°.李师傅找到BC边的中点P,连接AP,DP,发现△APD是直角三角形,请通过计算说明理由.
2.如图,在一次数学实践活动课上,老师让甲、乙两名同学同时从操场上的同一地点O出发,分别沿一固定方向行走.甲的速度是每分钟16 m,乙的速度是每分钟12 m,步行5分钟后,两人分别到达A,B两点,此时测得AB=100 m,如果甲同学沿西北方向前行,请判断乙同学行走的方向,并说明理由.
3.某中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的平均步行速度为30 m/min,第二组的平均步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1500 m.
(1)请通过计算判断这两组同学行走的方向是否成直角.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇
4.如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长.
(2)求喷泉B到小路AC的最短距离.
【练能力】
5.如图,一条伸直的橡皮筋AB的两端被固定在水平桌面上,C是AB上的一点,AB=5 cm,AC=4 cm,将橡皮筋从C点向上垂直拉升2 cm到D点.
(1)求橡皮筋比原来拉长的长度.
(2)判断△ABD的形状,并说明理由.
6.海洋上有一近似于四边形的岛屿,其平面如图1所示,小明据此构造出该岛的一个数学模型(如图2所示的四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5 km,CD= km,AD=4 km.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
【练素养】
7.如图,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A,D,B在同一条直线上),并新修一条路CD,测得CA=6.5千米,CD=6千米,AD=2.5千米.
(1)问CD是否为从村庄C到河边最近的路 请判断并说明理由.
(2)求原来的路BC的长.
参考答案
【练基础】
1.【解析】∵P为BC的中点,
∴BP=CP=BC=12(cm).
在Rt△ABP中,∠B=90°,根据勾股定理可得AP==20(cm).
在Rt△DCP中,同理可得DP=15(cm).
∵152+202=252,
∴AP2+DP2=AD2,
∴∠APD=90°,△APD是直角三角形.
2.【解析】乙同学行走的方向是东北方向.
理由:由题意可知OA=16×5=80(m),OB=12×5=60(m).
∵AB=100(m),
∴OA2+OB2=802+602=10000(m2),AB2=1002=10000(m2),
∴OA2+OB2=AB2,
∴∠AOB=90°.
由已知得∠AON=45°,∴∠BON=45°,
∴乙同学行走的方向是东北方向.
3.【解析】(1)半小时以后,第一组的路程:30×30=900(m).
第二组的路程:40×30=1200(m).
∵9002+12002=15002,
∴两组同学行走的方向成直角.
(2)设x min后两组同学相遇.
根据题意得30x+40x=1500,
解得x=(min).
答:经过 min后两组同学才能相遇.
4.【解析】(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
(2)∵AB=250 m,AM=200 m,BM=150 m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150 m.
【练能力】
5.【解析】(1)∵AB=5 cm,AC=4 cm,CD=2 cm,
在Rt△ACD中,
AD===2(cm),
在Rt△BCD中,
DB===(cm),
AD+DB-AB=2+-5=(3-5)(cm).
答:橡皮筋比原来拉伸了(3-5)cm.
(2)△ABD是直角三角形,
理由:∵AB2=52=25,AD2+DB2=(2)2+()2=20+5=25,
∴AB2=AD2+DB2,
∴△ABD是直角三角形.
6.【解析】(1)∵∠B=90°,AB=BC=5 km,
∴AC===5(km),
∴小溪流AC的长为5 km.
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,
则∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD
=×5×5+××4
=+2km2.
∴四边形ABCD的面积为+2km2.
【练素养】
7.【解析】(1)是.
理由:∵62+2.52=6.52,∴CD2+AD2=AC2,
∴∠ADC=90°,∴CD⊥AB,
∴CD是从村庄C到河边最近的路.
(2)设BC=x千米,则BD=(x-2.5)千米.
∵∠BDC=90°,∴CD2+BD2=BC2,即62+(x-2.5)2=x2,解得x=8.45.
答:原来的路BC的长为8.45千米.
2
