2023-2024学年初中数学人教版八年级下册18.1.1.1 平行四边形的概念及其边、角的性质 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册18.1.1.1 平行四边形的概念及其边、角的性质 课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:08:44 | ||
图片预览

文档简介
18.1.1.1 平行四边形的概念及其边、角的性质
【练基础】
必备知识1 平行四边形的定义
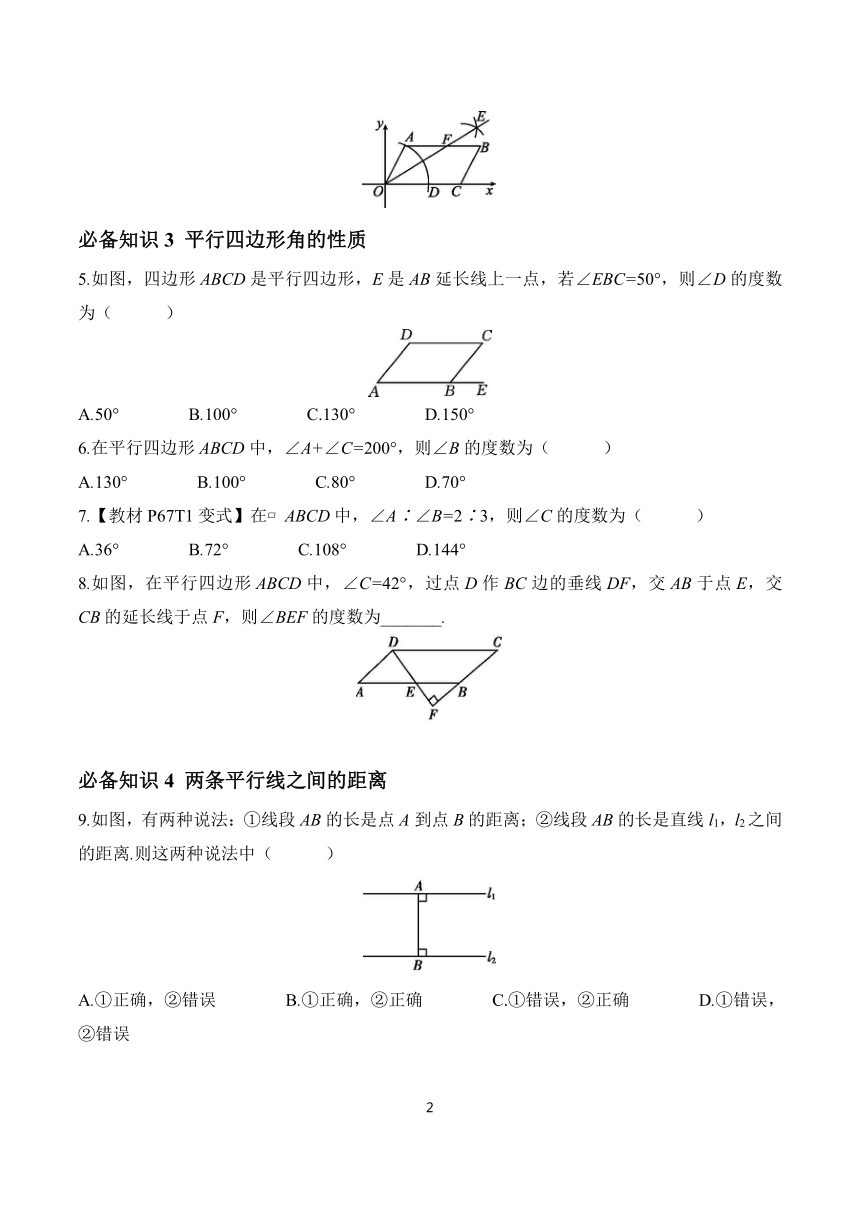
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)共有( )
A.9个 B.8个 C.6个 D.4个
必备知识2 平行四边形边的性质
2.【教材P50T8变式】如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
3.如图,在 ABCD中,CE平分∠BCD交AD于点E,若AE=2, ABCD的周长等于24,则AB的长为( )
A.5 B.6 C.7 D.8
4.如图, OABC的边OC在x轴上,点A的坐标为(1,2),点C的坐标为(4,0),以点O为圆心,OA的长为半径画弧,交x轴于点D,分别以点A,D为圆心,大于AD的长为半径画弧,两弧在∠AOC的内部交于点E,作射线OE,交AB于点F,则BF的长为________.
必备知识3 平行四边形角的性质
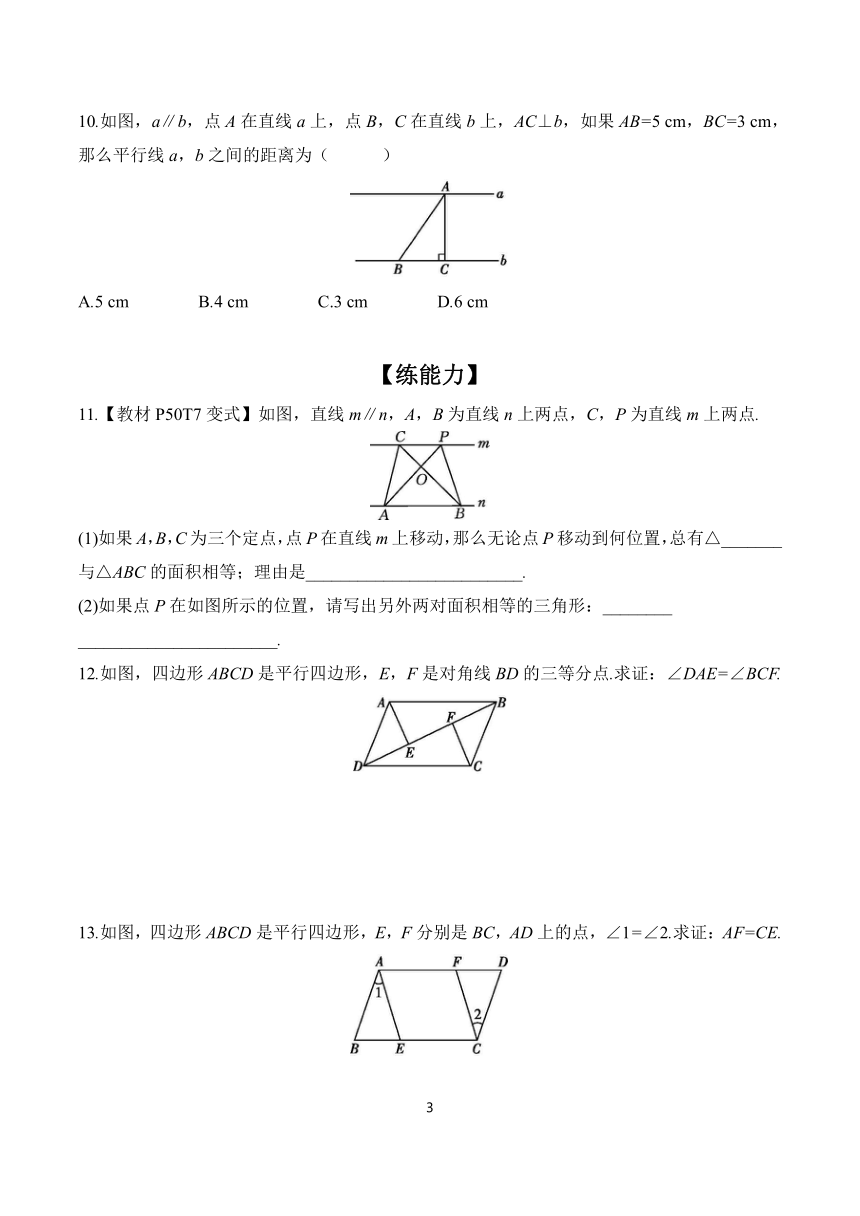
5.如图,四边形ABCD是平行四边形,E是AB延长线上一点,若∠EBC=50°,则∠D的度数为( )
A.50° B.100° C.130° D.150°
6.在平行四边形ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.130° B.100° C.80° D.70°
7.【教材P67T1变式】在 ABCD中,∠A∶∠B=2∶3,则∠C的度数为( )
A.36° B.72° C.108° D.144°
8.如图,在平行四边形ABCD中,∠C=42°,过点D作BC边的垂线DF,交AB于点E,交CB的延长线于点F,则∠BEF的度数为_______.
必备知识4 两条平行线之间的距离
9.如图,有两种说法:①线段AB的长是点A到点B的距离;②线段AB的长是直线l1,l2之间的距离.则这两种说法中( )
A.①正确,②错误 B.①正确,②正确 C.①错误,②正确 D.①错误,②错误
10.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5 cm,BC=3 cm,那么平行线a,b之间的距离为( )
A.5 cm B.4 cm C.3 cm D.6 cm
【练能力】
11.【教材P50T7变式】如图,直线m∥n,A,B为直线n上两点,C,P为直线m上两点.
(1)如果A,B,C为三个定点,点P在直线m上移动,那么无论点P移动到何位置,总有△_______与△ABC的面积相等;理由是_________________________.
(2)如果点P在如图所示的位置,请写出另外两对面积相等的三角形:________
_______________________.
12.如图,四边形ABCD是平行四边形,E,F是对角线BD的三等分点.求证:∠DAE=∠BCF.
13.如图,四边形ABCD是平行四边形,E,F分别是BC,AD上的点,∠1=∠2.求证:AF=CE.
14.如图,在 ABCD中,E是DC边上一点,连接AE,BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
(1)求证:DE=CE.
(2)若AE=4,BE=3,求 ABCD的周长与面积.
【练素养】
15.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若∠AED=70°,求∠ACD的度数.
(3)若AB=5,BE=6,EC=1,求DE的长.
参考答案
【练基础】
1.B 2.C 3.A 4.4-
5.C 【解析】解法一 ∵∠EBC=50°,∴∠ABC=130°.∵四边形ABCD是平行四边形,∴∠D=∠ABC=130°.
解法二 ∵四边形ABCD是平行四边形,∴BC∥AD,AB∥CD,∴∠A=∠EBC=50°,∠A+∠D=180°,
∴∠D=180°-∠A=130°.
6.C 7.B 8.48° 9.B 10.B
【练能力】
11.(1)PAB;同底等高的两个三角形的面积相等
(2)△PAC与△PBC,△OAC与△OBP
12.【证明】∵四边形ABCD为平行四边形,
∴AD∥CB,AD=CB,∠ADE=∠CBF.
∵E,F是对角线BD的三等分点,
∴DE=BF,
∴△ADE≌△CBF(SAS),
∴∠DAE=∠BCF.
13.【证明】∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,AD=BC.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),∴BE=DF.
∵AD=BC,∴AD-DF=BC-BE,
即AF=CE.
14.【解析】(1)证明:∵AE是∠DAB的平分线,BE是∠CBA的平分线,
∴∠DAE=∠EAB,∠CBE=∠ABE.
∵DC∥AB,
∴∠DEA=∠EAB,∠CEB=∠EBA,
∴∠DAE=∠DEA,∠CEB=∠CBE,
∴AD=DE,BC=CE.
∵四边形ABCD是平行四边形,
∴AD=BC,
∴DE=CE.
(2)∵AE是∠DAB的平分线,BE是∠CBA的平分线,
∴∠DAE=∠EAB,∠CBE=∠ABE.
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°.
∵AE=4,BE=3,
∴S△ABE=AE×BE=×4×3=6,
∴ ABCD的面积=2S△ABE=2×6=12.
∵∠AEB=90°,AE=4,BE=3,
∴AB===5.
由(1)可得AD=BC=DC=AB,
∴ ABCD的周长=AD+DC+BC+AB=2AB+AB=15.
【练素养】
15.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠AEB=∠EAD.
∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD.
在△ABC和△EAD中,
∴△ABC≌△EAD(SAS).
(2)由(1)得△ABC≌△EAD,
∴∠BAC=∠AED=70°.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ACD=∠BAC=70°.
(3)如图,过点A作AF⊥BC于点F.
∵AB=AE,
∴BF=FE=BE=3,FC=FE+EC=4.
在Rt△ABF和Rt△AFC中,
由勾股定理得AF===4,AC===4.
由(1)得△ABC≌△EAD,
∴DE=AC=4.
2
【练基础】
必备知识1 平行四边形的定义
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)共有( )
A.9个 B.8个 C.6个 D.4个
必备知识2 平行四边形边的性质
2.【教材P50T8变式】如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
3.如图,在 ABCD中,CE平分∠BCD交AD于点E,若AE=2, ABCD的周长等于24,则AB的长为( )
A.5 B.6 C.7 D.8
4.如图, OABC的边OC在x轴上,点A的坐标为(1,2),点C的坐标为(4,0),以点O为圆心,OA的长为半径画弧,交x轴于点D,分别以点A,D为圆心,大于AD的长为半径画弧,两弧在∠AOC的内部交于点E,作射线OE,交AB于点F,则BF的长为________.
必备知识3 平行四边形角的性质
5.如图,四边形ABCD是平行四边形,E是AB延长线上一点,若∠EBC=50°,则∠D的度数为( )
A.50° B.100° C.130° D.150°
6.在平行四边形ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.130° B.100° C.80° D.70°
7.【教材P67T1变式】在 ABCD中,∠A∶∠B=2∶3,则∠C的度数为( )
A.36° B.72° C.108° D.144°
8.如图,在平行四边形ABCD中,∠C=42°,过点D作BC边的垂线DF,交AB于点E,交CB的延长线于点F,则∠BEF的度数为_______.
必备知识4 两条平行线之间的距离
9.如图,有两种说法:①线段AB的长是点A到点B的距离;②线段AB的长是直线l1,l2之间的距离.则这两种说法中( )
A.①正确,②错误 B.①正确,②正确 C.①错误,②正确 D.①错误,②错误
10.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5 cm,BC=3 cm,那么平行线a,b之间的距离为( )
A.5 cm B.4 cm C.3 cm D.6 cm
【练能力】
11.【教材P50T7变式】如图,直线m∥n,A,B为直线n上两点,C,P为直线m上两点.
(1)如果A,B,C为三个定点,点P在直线m上移动,那么无论点P移动到何位置,总有△_______与△ABC的面积相等;理由是_________________________.
(2)如果点P在如图所示的位置,请写出另外两对面积相等的三角形:________
_______________________.
12.如图,四边形ABCD是平行四边形,E,F是对角线BD的三等分点.求证:∠DAE=∠BCF.
13.如图,四边形ABCD是平行四边形,E,F分别是BC,AD上的点,∠1=∠2.求证:AF=CE.
14.如图,在 ABCD中,E是DC边上一点,连接AE,BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
(1)求证:DE=CE.
(2)若AE=4,BE=3,求 ABCD的周长与面积.
【练素养】
15.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若∠AED=70°,求∠ACD的度数.
(3)若AB=5,BE=6,EC=1,求DE的长.
参考答案
【练基础】
1.B 2.C 3.A 4.4-
5.C 【解析】解法一 ∵∠EBC=50°,∴∠ABC=130°.∵四边形ABCD是平行四边形,∴∠D=∠ABC=130°.
解法二 ∵四边形ABCD是平行四边形,∴BC∥AD,AB∥CD,∴∠A=∠EBC=50°,∠A+∠D=180°,
∴∠D=180°-∠A=130°.
6.C 7.B 8.48° 9.B 10.B
【练能力】
11.(1)PAB;同底等高的两个三角形的面积相等
(2)△PAC与△PBC,△OAC与△OBP
12.【证明】∵四边形ABCD为平行四边形,
∴AD∥CB,AD=CB,∠ADE=∠CBF.
∵E,F是对角线BD的三等分点,
∴DE=BF,
∴△ADE≌△CBF(SAS),
∴∠DAE=∠BCF.
13.【证明】∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,AD=BC.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),∴BE=DF.
∵AD=BC,∴AD-DF=BC-BE,
即AF=CE.
14.【解析】(1)证明:∵AE是∠DAB的平分线,BE是∠CBA的平分线,
∴∠DAE=∠EAB,∠CBE=∠ABE.
∵DC∥AB,
∴∠DEA=∠EAB,∠CEB=∠EBA,
∴∠DAE=∠DEA,∠CEB=∠CBE,
∴AD=DE,BC=CE.
∵四边形ABCD是平行四边形,
∴AD=BC,
∴DE=CE.
(2)∵AE是∠DAB的平分线,BE是∠CBA的平分线,
∴∠DAE=∠EAB,∠CBE=∠ABE.
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°.
∵AE=4,BE=3,
∴S△ABE=AE×BE=×4×3=6,
∴ ABCD的面积=2S△ABE=2×6=12.
∵∠AEB=90°,AE=4,BE=3,
∴AB===5.
由(1)可得AD=BC=DC=AB,
∴ ABCD的周长=AD+DC+BC+AB=2AB+AB=15.
【练素养】
15.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠AEB=∠EAD.
∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD.
在△ABC和△EAD中,
∴△ABC≌△EAD(SAS).
(2)由(1)得△ABC≌△EAD,
∴∠BAC=∠AED=70°.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ACD=∠BAC=70°.
(3)如图,过点A作AF⊥BC于点F.
∵AB=AE,
∴BF=FE=BE=3,FC=FE+EC=4.
在Rt△ABF和Rt△AFC中,
由勾股定理得AF===4,AC===4.
由(1)得△ABC≌△EAD,
∴DE=AC=4.
2
