2023-2024学年初中数学人教版八年级下册18.1.2.2 平行四边形的判定(2) 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册18.1.2.2 平行四边形的判定(2) 课时练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 99.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:11:10 | ||
图片预览


文档简介
18.1.2.2 平行四边形的判定(2)
【练基础】
必备知识 一组对边平行且相等的四边形是平行四边形
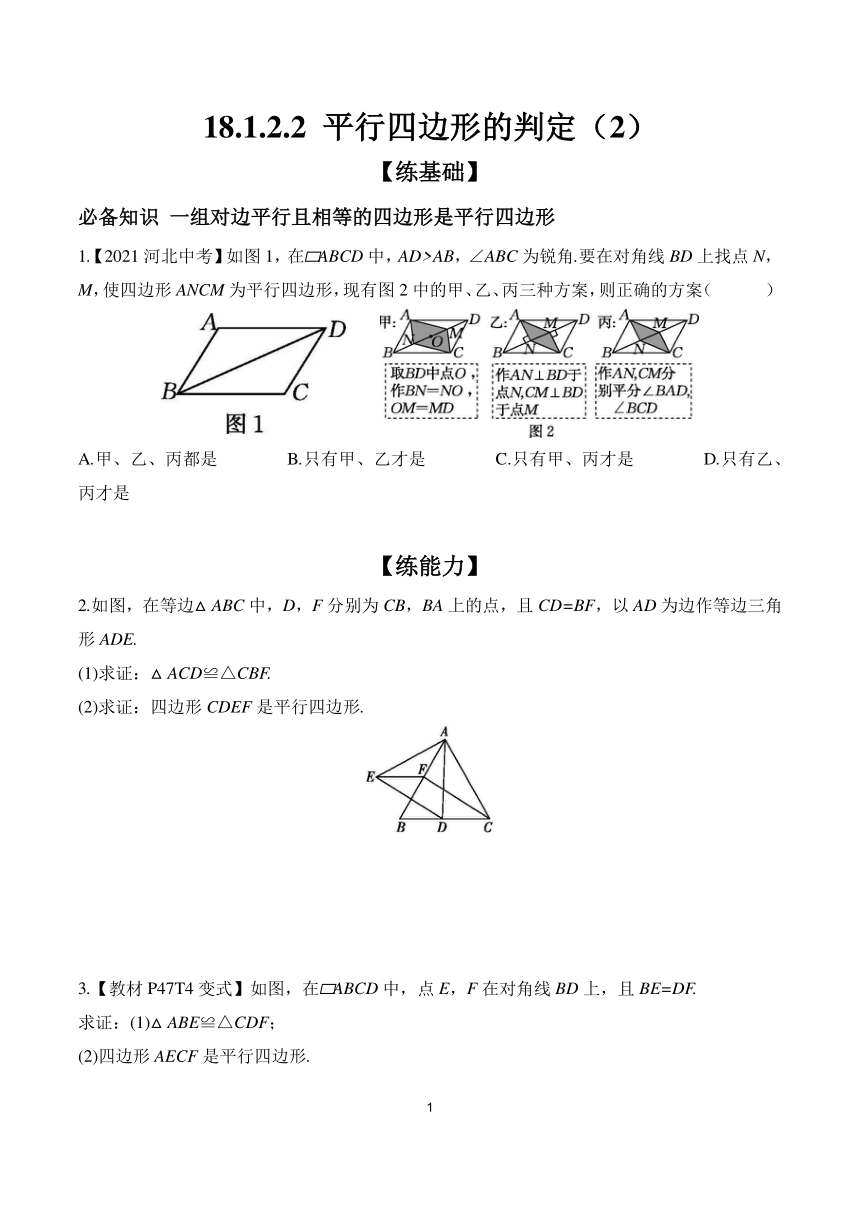
1.【2021河北中考】如图1,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
A.甲、乙、丙都是 B.只有甲、乙才是 C.只有甲、丙才是 D.只有乙、丙才是
【练能力】
2.如图,在等边△ABC中,D,F分别为CB,BA上的点,且CD=BF,以AD为边作等边三角形ADE.
(1)求证:△ACD≌△CBF.
(2)求证:四边形CDEF是平行四边形.
3.【教材P47T4变式】如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【练素养】
4.如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰三角形ADE,且∠ADE=∠ABC,连接CE,过点E作EM∥BC交CA的延长线于点M,连接BM.
(1)求证:△BAD≌△CAE.
(2)若∠ABC=30°,求∠MEC的度数.
(3)求证:四边形MBDE是平行四边形.
参考答案
【练基础】
1.A 【解析】对于甲方案,连接AC(图略).因为四边形ABCD是平行四边形,所以AC经过BD的中点O,且AO=CO.又因为BO=DO,BN=NO,OM=MD,所以NO=OM,所以四边形ANCM是平行四边形.对于乙方案,易证△ABN≌△CDM,所以AN=CM.因为AN⊥BD,CM⊥BD,所以AN∥CM,所以四边形ANCM是平行四边形.对于丙方案,易证△BAN≌△DCM,所以AN=CM,∠ANB=∠CMD,所以∠ANM=∠CMN,所以AN∥CM,所以四边形ANCM是平行四边形.综上可知,甲、乙、丙三种方案都是正确的.
【练能力】
2.【证明】(1)∵△ABC为等边三角形,
∴AC=CB,∠ACD=∠CBF=60°.
在△ACD和△CBF中,
∴△ACD≌△CBF(SAS).
(2)∵△ACD≌△CBF,
∴AD=CF,∠CAD=∠BCF.
∵△AED为等边三角形,∴∠ADE=60°,
且AD=DE,∴CF=DE.
∵∠EDB+60°=∠BDA=∠CAD+∠ACD=∠BCF+60°,
∴∠EDB=∠BCF,∴ED∥FC,
∴四边形CDEF为平行四边形.
3.【证明】(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,∴∠ABD=∠CDB(SAS).
在△ABE和△CDF中,
∴△ABE≌△CDF.
(2)证法一 由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,∴AE∥CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
证法二 由(1)可知,△ABE≌△CDF,
∴AE=CF,
同(1)可得△ADF≌△CBE,∴AF=CE.
∵AE=CF,AF=CE,
∴四边形AECF是平行四边形.
【练素养】
4.【解析】(1)证明:∵AB=AC,∴∠ABC=∠ACB,
∴∠BAC=180°-2∠ABC.
∵以AD,AE为腰作等腰三角形ADE,
∴AD=AE,∴∠ADE=∠AED,
∴∠DAE=180°-2∠ADE.
∵∠ADE=∠ABC,∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)∵AB=AC,∴∠ACB=∠ABC=30°.
∵△BAD≌△CAE,
∴∠ABD=∠ACE=30°,
∴∠ACB=∠ACE=30°,
∴∠ECB=∠ACB+∠ACE=60°.
∵EM∥BC,∴∠MEC+∠ECD=180°,
∴∠MEC=180°-60°=120°.
(3)证明:∵△BAD≌△CAE,
∴DB=EC,∠ABD=∠ACE.
∵AB=AC,∴∠ABD=∠ACB,
∴∠ACB=∠ACE.
∵EM∥BC,∴∠EMC=∠ACB,
∴∠ACE=∠EMC,
∴ME=EC,
∴DB=ME.
又∵EM∥BD,∴四边形MBDE是平行四边形.
2
【练基础】
必备知识 一组对边平行且相等的四边形是平行四边形
1.【2021河北中考】如图1,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
A.甲、乙、丙都是 B.只有甲、乙才是 C.只有甲、丙才是 D.只有乙、丙才是
【练能力】
2.如图,在等边△ABC中,D,F分别为CB,BA上的点,且CD=BF,以AD为边作等边三角形ADE.
(1)求证:△ACD≌△CBF.
(2)求证:四边形CDEF是平行四边形.
3.【教材P47T4变式】如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【练素养】
4.如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰三角形ADE,且∠ADE=∠ABC,连接CE,过点E作EM∥BC交CA的延长线于点M,连接BM.
(1)求证:△BAD≌△CAE.
(2)若∠ABC=30°,求∠MEC的度数.
(3)求证:四边形MBDE是平行四边形.
参考答案
【练基础】
1.A 【解析】对于甲方案,连接AC(图略).因为四边形ABCD是平行四边形,所以AC经过BD的中点O,且AO=CO.又因为BO=DO,BN=NO,OM=MD,所以NO=OM,所以四边形ANCM是平行四边形.对于乙方案,易证△ABN≌△CDM,所以AN=CM.因为AN⊥BD,CM⊥BD,所以AN∥CM,所以四边形ANCM是平行四边形.对于丙方案,易证△BAN≌△DCM,所以AN=CM,∠ANB=∠CMD,所以∠ANM=∠CMN,所以AN∥CM,所以四边形ANCM是平行四边形.综上可知,甲、乙、丙三种方案都是正确的.
【练能力】
2.【证明】(1)∵△ABC为等边三角形,
∴AC=CB,∠ACD=∠CBF=60°.
在△ACD和△CBF中,
∴△ACD≌△CBF(SAS).
(2)∵△ACD≌△CBF,
∴AD=CF,∠CAD=∠BCF.
∵△AED为等边三角形,∴∠ADE=60°,
且AD=DE,∴CF=DE.
∵∠EDB+60°=∠BDA=∠CAD+∠ACD=∠BCF+60°,
∴∠EDB=∠BCF,∴ED∥FC,
∴四边形CDEF为平行四边形.
3.【证明】(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,∴∠ABD=∠CDB(SAS).
在△ABE和△CDF中,
∴△ABE≌△CDF.
(2)证法一 由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,∴AE∥CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
证法二 由(1)可知,△ABE≌△CDF,
∴AE=CF,
同(1)可得△ADF≌△CBE,∴AF=CE.
∵AE=CF,AF=CE,
∴四边形AECF是平行四边形.
【练素养】
4.【解析】(1)证明:∵AB=AC,∴∠ABC=∠ACB,
∴∠BAC=180°-2∠ABC.
∵以AD,AE为腰作等腰三角形ADE,
∴AD=AE,∴∠ADE=∠AED,
∴∠DAE=180°-2∠ADE.
∵∠ADE=∠ABC,∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)∵AB=AC,∴∠ACB=∠ABC=30°.
∵△BAD≌△CAE,
∴∠ABD=∠ACE=30°,
∴∠ACB=∠ACE=30°,
∴∠ECB=∠ACB+∠ACE=60°.
∵EM∥BC,∴∠MEC+∠ECD=180°,
∴∠MEC=180°-60°=120°.
(3)证明:∵△BAD≌△CAE,
∴DB=EC,∠ABD=∠ACE.
∵AB=AC,∴∠ABD=∠ACB,
∴∠ACB=∠ACE.
∵EM∥BC,∴∠EMC=∠ACB,
∴∠ACE=∠EMC,
∴ME=EC,
∴DB=ME.
又∵EM∥BD,∴四边形MBDE是平行四边形.
2
