2023-2024学年初中数学人教版八年级下册18.2.1.1 矩形的性质 课时练习 (含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册18.2.1.1 矩形的性质 课时练习 (含解析) | 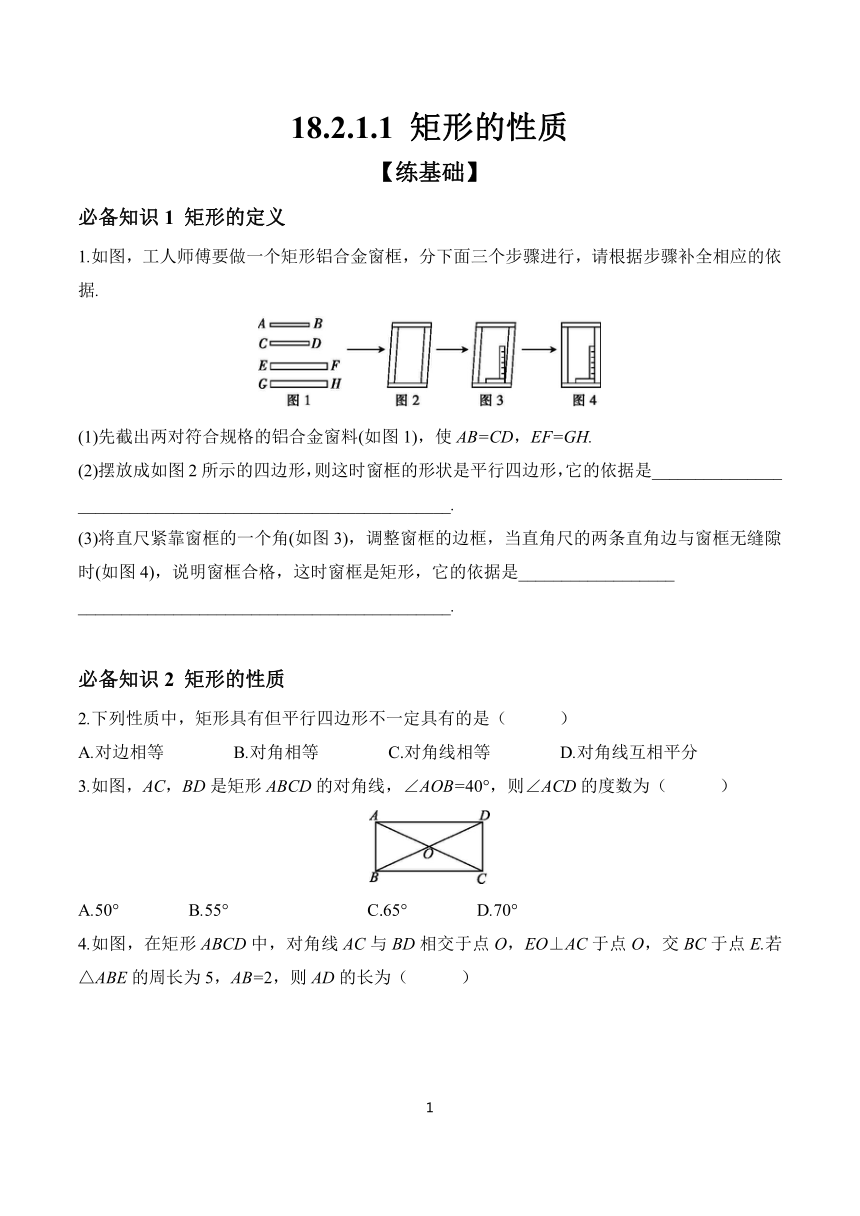 | |
| 格式 | docx | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:12:14 | ||
图片预览


文档简介
18.2.1.1 矩形的性质
【练基础】
必备知识1 矩形的定义
1.如图,工人师傅要做一个矩形铝合金窗框,分下面三个步骤进行,请根据步骤补全相应的依据.
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD,EF=GH.
(2)摆放成如图2所示的四边形,则这时窗框的形状是平行四边形,它的依据是_______________
___________________________________________.
(3)将直尺紧靠窗框的一个角(如图3),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是矩形,它的依据是__________________
___________________________________________.
必备知识2 矩形的性质
2.下列性质中,矩形具有但平行四边形不一定具有的是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
3.如图,AC,BD是矩形ABCD的对角线,∠AOB=40°,则∠ACD的度数为( )
A.50° B.55° C.65° D.70°
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E.若△ABE的周长为5,AB=2,则AD的长为( )
A.2 B.2.5 C.3 D.4
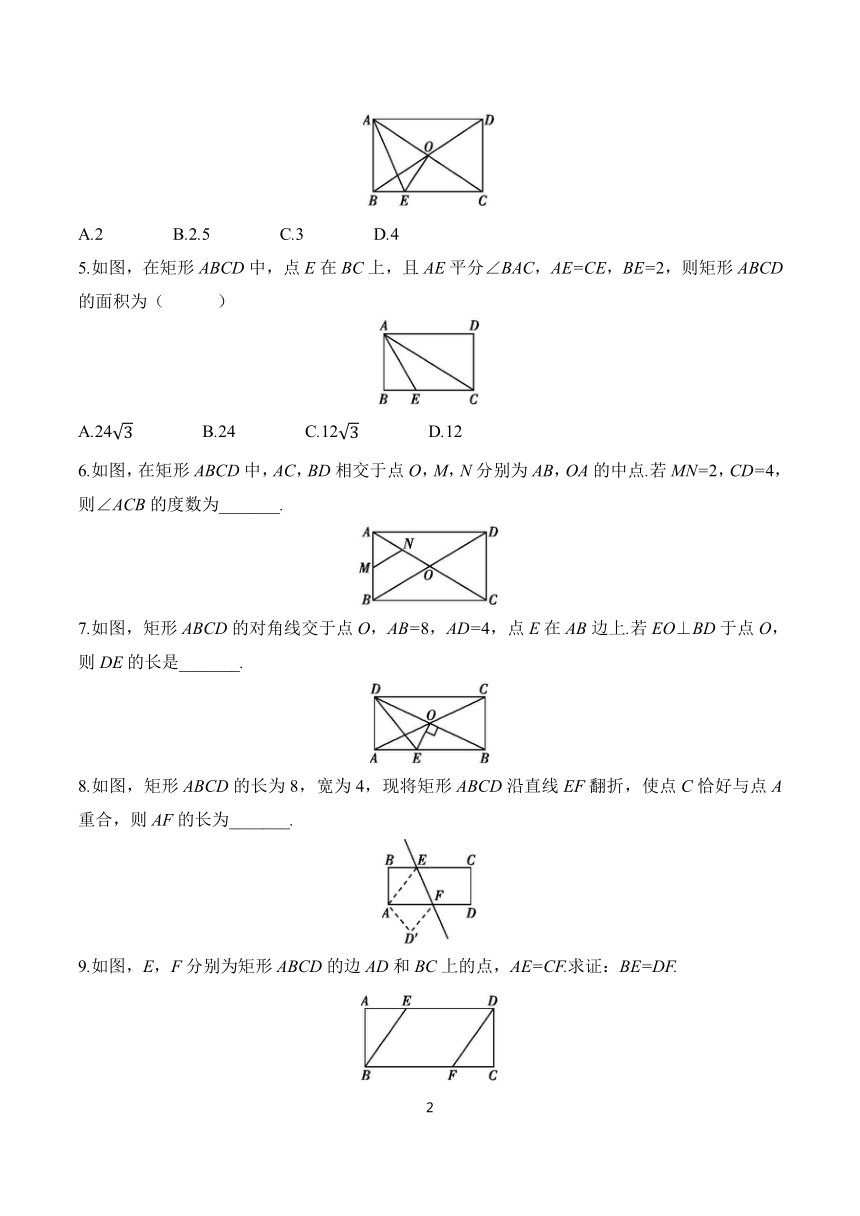
5.如图,在矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
6.如图,在矩形ABCD中,AC,BD相交于点O,M,N分别为AB,OA的中点.若MN=2,CD=4,则∠ACB的度数为_______.
7.如图,矩形ABCD的对角线交于点O,AB=8,AD=4,点E在AB边上.若EO⊥BD于点O,则DE的长是_______.
8.如图,矩形ABCD的长为8,宽为4,现将矩形ABCD沿直线EF翻折,使点C恰好与点A重合,则AF的长为_______.
9.如图,E,F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
必备知识3 直角三角形斜边上的中线的性质
10.如图,在△ABC中,∠ACB=90°,∠B=55°,D是斜边AB的中点,那么∠ACD的度数为( )
A.15° B.25° C.35° D.45°
11.如图,E是△ABC内一点,∠AEB=90°,D是边AB的中点,延长线段DE交边BC于点F,F是边BC的中点,若AB=6,EF=1,则线段AC的长为_______.
【练能力】
12.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,M,N分别是BC,DE的中点.
(1)求证:MN⊥DE.
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
13.如图,在矩形ABCD中,点E在BC上,DF⊥AE,垂足为F,DF=AB.
(1)求证:AE=BC.
(2)若∠FDC=30°,且AB=4,连接DE,求∠DEF的大小和AD的长.
【练素养】
14.如图,将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E.
(1)求证:△ADE≌△CB'E.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于点G,PH⊥DC于点H,求PG+PH的值.
参考答案
【练基础】
1.(2)两组对边分别相等的四边形是平行四边形
(3)有一个角是直角的平行四边形是矩形
2.C 3.D 4.C 5.C 6.30° 7.5 8.5
9.【证明】∵四边形ABCD为矩形,∴AD∥BC,AD=BC.
又∵AE=CF,∴AD-AE=BC-CF,即ED=BF,而ED∥BF,
∴四边形BFDE为平行四边形,∴BE=DF(平行四边形对边相等).
10.C 【解析】解法一 在△ABC中,∠ACB=90°.
∵D是斜边AB的中点,
∴CD=BD=AB,∴∠B=∠DCB=55°.
又∵∠ACB=90°,∴∠ACD=90°-55°=35°.
解法二 ∵∠ACB=90°,∠B=55°,
∴∠A=180°-∠ACB-∠B=35°.
∵D是斜边AB的中点,∴CD=AD=AB,
∴∠ACD=∠A=35°.
11.8
【练能力】
12.【解析】(1)证明:如图,连接DM,EM.
∵BD⊥AC于点D,CE⊥AB于点E,M是BC的中点,
∴MD=ME=BC.
∵N是DE的中点,
∴MN⊥DE.
(2)△EDM是等边三角形.
理由:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°-2∠ABC+180°-2∠ACB=360°-2(∠ABC+∠ACB).
∵∠A=60°,∴∠ABC+∠ACB=180°-60°=120°,
∴∠BME+∠CMD=360°-2×120°=120°,
∴∠DME=60°,∴△EDM是等边三角形.
13.【解析】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=∠ADC,
∴∠DAE=∠AEB.
在△ABE与△DFA中,
∴△ABE≌△DFA(AAS),∴AE=AD.
∵AD=BC,∴AE=BC.
(2)∵DF⊥AE,∠C=90°,∴∠DFE=∠DCE.
∵AB=DF,AB=DC,∴DF=DC.
在Rt△DEF与Rt△DEC中,
∴Rt△DEF≌Rt△DEC(HL),∴∠FDE=∠CDE.
∵∠FDC=30°,∴∠FDE=∠CDE=30°÷2=15°,
∴∠DEF=180°-90°-15°=75°.
∵△ABE≌△DFA,AB=4,∴DF=4.
∵∠FDC=30°,∴∠ADF=90°-30°=60°,
∴∠DAE=180°-90°-60°=30°.
∵DF=4,∴AD=4×2=8.
因此,∠DEF=75°,AD=8.
【练素养】
14.【解析】(1)证明:∵将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,
∴CB'=CB,∠EB'C=∠CBA=90°.
∵四边形ABCD是矩形,
∴AD=BC=B'C,∠ADE=90°.
在△ADE和△CB'E中,
∴△ADE≌△CB'E(AAS).
(2)如图,连接PE.
由(1)知△ADE≌△CB'E,
∴AE=EC.
∵四边形ABCD是矩形,∴CD=AB,
∴CE=CD-DE=AB-DE=8-3=5=AE,
∴AD==4.
∵S△AEP+S△ECP=S△ECA,
∴AE·PG+EC·PH=EC·AD,
∴PG+PH=AD=4.
2
【练基础】
必备知识1 矩形的定义
1.如图,工人师傅要做一个矩形铝合金窗框,分下面三个步骤进行,请根据步骤补全相应的依据.
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD,EF=GH.
(2)摆放成如图2所示的四边形,则这时窗框的形状是平行四边形,它的依据是_______________
___________________________________________.
(3)将直尺紧靠窗框的一个角(如图3),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是矩形,它的依据是__________________
___________________________________________.
必备知识2 矩形的性质
2.下列性质中,矩形具有但平行四边形不一定具有的是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
3.如图,AC,BD是矩形ABCD的对角线,∠AOB=40°,则∠ACD的度数为( )
A.50° B.55° C.65° D.70°
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E.若△ABE的周长为5,AB=2,则AD的长为( )
A.2 B.2.5 C.3 D.4
5.如图,在矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
6.如图,在矩形ABCD中,AC,BD相交于点O,M,N分别为AB,OA的中点.若MN=2,CD=4,则∠ACB的度数为_______.
7.如图,矩形ABCD的对角线交于点O,AB=8,AD=4,点E在AB边上.若EO⊥BD于点O,则DE的长是_______.
8.如图,矩形ABCD的长为8,宽为4,现将矩形ABCD沿直线EF翻折,使点C恰好与点A重合,则AF的长为_______.
9.如图,E,F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
必备知识3 直角三角形斜边上的中线的性质
10.如图,在△ABC中,∠ACB=90°,∠B=55°,D是斜边AB的中点,那么∠ACD的度数为( )
A.15° B.25° C.35° D.45°
11.如图,E是△ABC内一点,∠AEB=90°,D是边AB的中点,延长线段DE交边BC于点F,F是边BC的中点,若AB=6,EF=1,则线段AC的长为_______.
【练能力】
12.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,M,N分别是BC,DE的中点.
(1)求证:MN⊥DE.
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
13.如图,在矩形ABCD中,点E在BC上,DF⊥AE,垂足为F,DF=AB.
(1)求证:AE=BC.
(2)若∠FDC=30°,且AB=4,连接DE,求∠DEF的大小和AD的长.
【练素养】
14.如图,将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E.
(1)求证:△ADE≌△CB'E.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于点G,PH⊥DC于点H,求PG+PH的值.
参考答案
【练基础】
1.(2)两组对边分别相等的四边形是平行四边形
(3)有一个角是直角的平行四边形是矩形
2.C 3.D 4.C 5.C 6.30° 7.5 8.5
9.【证明】∵四边形ABCD为矩形,∴AD∥BC,AD=BC.
又∵AE=CF,∴AD-AE=BC-CF,即ED=BF,而ED∥BF,
∴四边形BFDE为平行四边形,∴BE=DF(平行四边形对边相等).
10.C 【解析】解法一 在△ABC中,∠ACB=90°.
∵D是斜边AB的中点,
∴CD=BD=AB,∴∠B=∠DCB=55°.
又∵∠ACB=90°,∴∠ACD=90°-55°=35°.
解法二 ∵∠ACB=90°,∠B=55°,
∴∠A=180°-∠ACB-∠B=35°.
∵D是斜边AB的中点,∴CD=AD=AB,
∴∠ACD=∠A=35°.
11.8
【练能力】
12.【解析】(1)证明:如图,连接DM,EM.
∵BD⊥AC于点D,CE⊥AB于点E,M是BC的中点,
∴MD=ME=BC.
∵N是DE的中点,
∴MN⊥DE.
(2)△EDM是等边三角形.
理由:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°-2∠ABC+180°-2∠ACB=360°-2(∠ABC+∠ACB).
∵∠A=60°,∴∠ABC+∠ACB=180°-60°=120°,
∴∠BME+∠CMD=360°-2×120°=120°,
∴∠DME=60°,∴△EDM是等边三角形.
13.【解析】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=∠ADC,
∴∠DAE=∠AEB.
在△ABE与△DFA中,
∴△ABE≌△DFA(AAS),∴AE=AD.
∵AD=BC,∴AE=BC.
(2)∵DF⊥AE,∠C=90°,∴∠DFE=∠DCE.
∵AB=DF,AB=DC,∴DF=DC.
在Rt△DEF与Rt△DEC中,
∴Rt△DEF≌Rt△DEC(HL),∴∠FDE=∠CDE.
∵∠FDC=30°,∴∠FDE=∠CDE=30°÷2=15°,
∴∠DEF=180°-90°-15°=75°.
∵△ABE≌△DFA,AB=4,∴DF=4.
∵∠FDC=30°,∴∠ADF=90°-30°=60°,
∴∠DAE=180°-90°-60°=30°.
∵DF=4,∴AD=4×2=8.
因此,∠DEF=75°,AD=8.
【练素养】
14.【解析】(1)证明:∵将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,
∴CB'=CB,∠EB'C=∠CBA=90°.
∵四边形ABCD是矩形,
∴AD=BC=B'C,∠ADE=90°.
在△ADE和△CB'E中,
∴△ADE≌△CB'E(AAS).
(2)如图,连接PE.
由(1)知△ADE≌△CB'E,
∴AE=EC.
∵四边形ABCD是矩形,∴CD=AB,
∴CE=CD-DE=AB-DE=8-3=5=AE,
∴AD==4.
∵S△AEP+S△ECP=S△ECA,
∴AE·PG+EC·PH=EC·AD,
∴PG+PH=AD=4.
2
