2023-2024学年初中数学人教版八年级下册18.2.1.2 矩形的判定 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册18.2.1.2 矩形的判定 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:13:01 | ||
图片预览


文档简介
18.2.1.2 矩形的判定
【练基础】
必备知识1 有一个角是直角的平行四边形是矩形
1.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
2.如图,在 ABCD中,点E,F在AD边上,且BF=CE,AE=DF.
(1)求证:△ABF≌△DCE.
(2)求证:四边形ABCD是矩形.
必备知识2 对角线相等的平行四边形是矩形
3.【邯郸期末】四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AC=BD B.∠ABD=∠CBD C.AB=BD D.AB=CD
4.如图,在 ABCD中,E为DC的中点,连接AE并延长交BC的延长线于点F,连接AC,DF.
(1)求证:AD=CF.
(2)嘉琪说:“添加一个条件,能使四边形ACFD是矩形”,你是否同意嘉琪的观点 如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
必备知识3 有三个角是直角的四边形是矩形
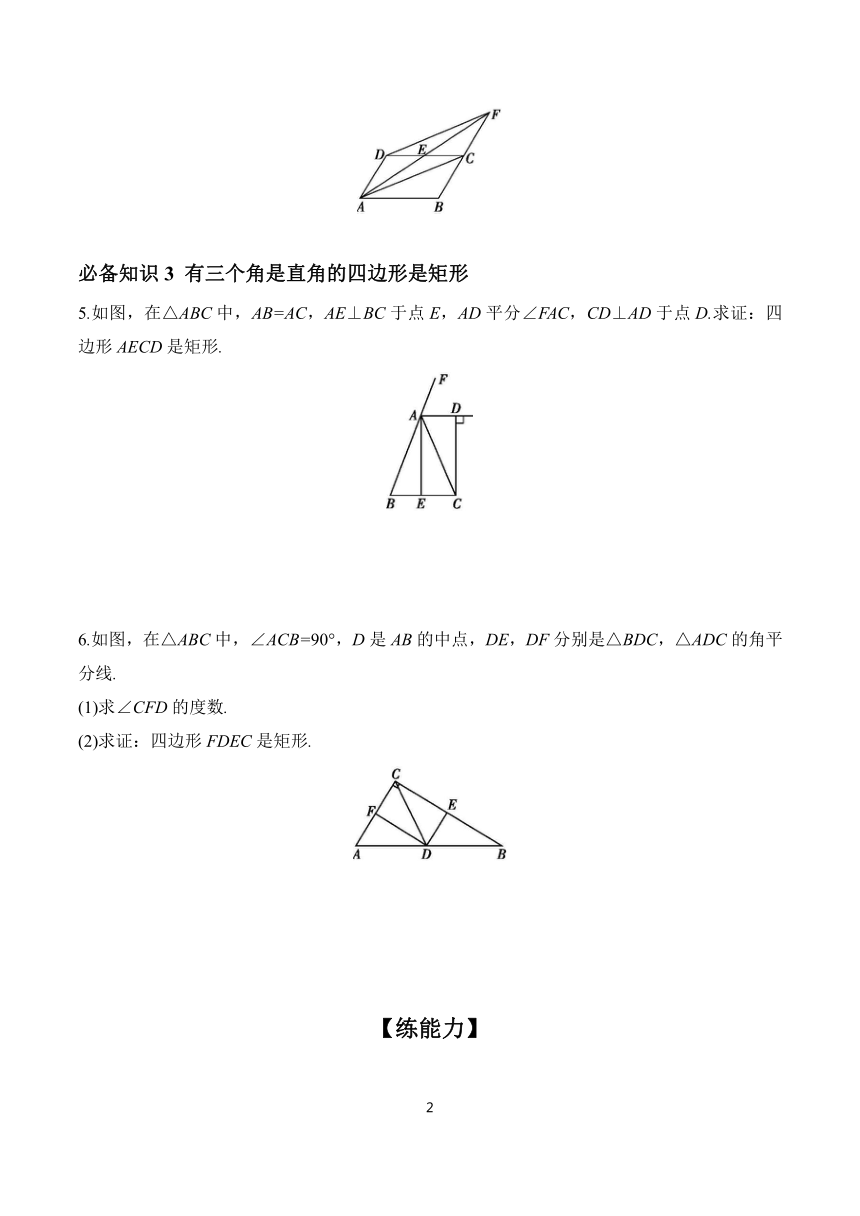
5.如图,在△ABC中,AB=AC,AE⊥BC于点E,AD平分∠FAC,CD⊥AD于点D.求证:四边形AECD是矩形.
6.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE,DF分别是△BDC,△ADC的角平分线.
(1)求∠CFD的度数.
(2)求证:四边形FDEC是矩形.
【练能力】
7.【教材P68T9变式】如图,连接四边形ABCD各边中点得到四边形EFGH,还要添加_______才能使四边形EFGH是矩形.(写出一个条件即可,图中不能再添加别的“点”或“线”)
8.如图,在 ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF.
(2)设=k,当k为何值时,四边形DEBF是矩形 请说明理由.
9.如图,已知点M,O,N在同一直线上,OB,OC分别是∠AOM与∠AON的平分线,AB⊥OB,AC⊥OC,垂足分别为B,C,连接BC交AO于点E.
(1)求证:四边形ACOB是矩形.
(2)猜想BC与MN的位置关系,并证明你的结论.
10.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形.
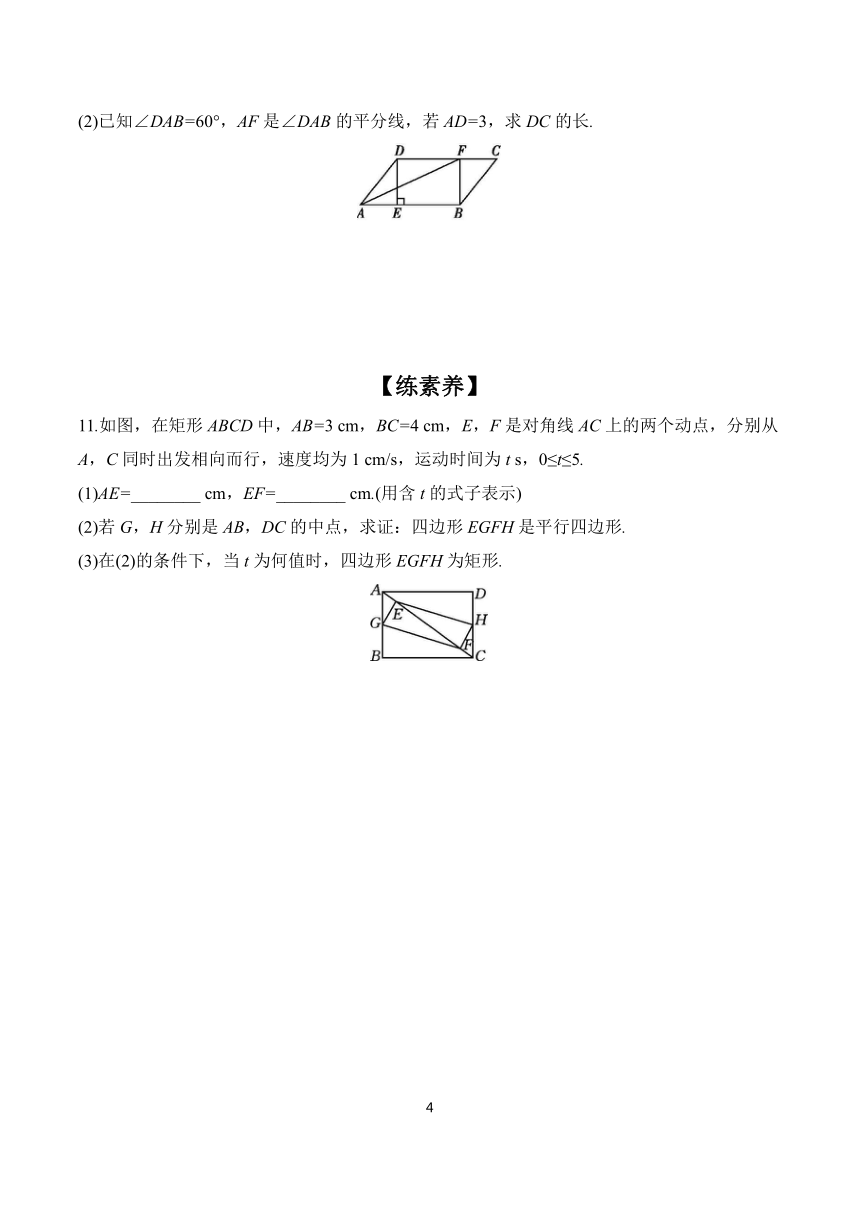
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长.
【练素养】
11.如图,在矩形ABCD中,AB=3 cm,BC=4 cm,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1 cm/s,运动时间为t s,0≤t≤5.
(1)AE=________ cm,EF=________ cm.(用含t的式子表示)
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)的条件下,当t为何值时,四边形EGFH为矩形.
参考答案
【练基础】
1.C
2.【证明】(1)∵四边形ABCD是平行四边形,∴AB=CD.
∵AE=FD,∴AE+EF=FD+EF,即AF=DE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SSS).
(2)由(1)可知△ABF≌△DCE,∴∠A=∠D.
∵四边形ABCD是平行四边形,∴∠A+∠D=180°,∴2∠A=180°,∴∠A=90°,∴ ABCD是矩形.
3.A
4.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠CFE,∠ADE=∠FCE.
∵E为DC的中点,∴ED=EC,
∴△ADE≌△FCE(AAS),∴AD=CF.
(2)同意.当DC=AF时,四边形ACFD是矩形.
证明:∵AD∥CF,AD=CF,∴四边形ACFD是平行四边形.
∵DC=AF,∴四边形ACFD是矩形.
5.【证明】∵AB=AC,AE⊥BC于点E,
∴∠AEC=90°,∠BAE=∠CAE=∠BAC.
∵AD平分∠FAC,∴∠DAC=∠FAC,
∴∠DAE=∠DAC+∠CAE=∠BAC+∠FAC=(∠BAC+∠FAC)=×180°=90°.
又∵CD⊥AD于点D,∴∠ADC=90°,∴四边形AECD是矩形.
6.【解析】(1)∵∠ACB=90°,D是AB的中点,
∴BD=CD=AD.
∵DF是∠ADC的平分线,∴DF⊥AC.
∴∠CFD=90°.
(2)证明:∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD.
∵DE是∠BDC的平分线,∴DE⊥BC,
∴∠DEC=90°.
∵∠CFD=90°,∠ACB=90°,
∴四边形DECF是矩形.
【练能力】
7.AC⊥BD(答案不唯一)
8.【解析】(1)证明:解法一 如图,连接DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=OC.
∵E,F分别为AO,OC的中点,
∴EO=OA,OF=OC,
∴EO=FO.
∵BO=OD,EO=FO,
∴四边形BFDE是平行四边形,
∴BE=DF.
解法二 ∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,∴∠DCF=∠BAE.
∵E,F分别OA,OC的中点,
∴AE=OA,CF=OC,∴AE=CF.
在△DCF和△BAE中,
∴△DCF≌△BAE,∴BE=DF.
(2)当k=2时,四边形DEBF是矩形.理由如下:
易知四边形DEBF是平行四边形,
当BD=EF,即OD=OE时,四边形DEBF是矩形,
此时AE=OE,∴AO=2OE,则k====2,
∴当k=2时,四边形DEBF是矩形.
9.【解析】(1)证明:∵OB,OC分别是∠AOM与∠AON的平分线,
∴∠AOM=2∠AOB,∠AON=2∠AOC.
∵点M,O,N在同一直线上,∴∠AOM+∠AON=180°,
∴2∠AOB+2∠AOC=180°,∴∠AOB+∠AOC=90°,即∠BOC=90°.
∵AB⊥OB,AC⊥OC,∴∠ABO=∠ACO=90°,∴四边形ACOB是矩形.
(2)BC∥MN.证明:由(1)可得,四边形ACOB是矩形,∴OE=CE,
∴∠AOC=∠BCO.
∵OC是∠AON的平分线,∴∠AOC=∠NOC,
∴∠BCO=∠NOC,∴BC∥MN.
10.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵CF=AE,∴DF=BE.
又∵DC∥AB,∴四边形DFBE是平行四边形,
∵DE⊥AB,∴平行四边形BFDE是矩形.
(2)∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=,DE==.
由(1)可得四边形DFBE是矩形,
∴BF=DE=.
∵AF平分∠DAB,∴∠FAB=∠DAB=30°,且BF⊥AB,
∴AF=2BF=3,
∴AB==,∴CD=.
【练素养】
11.【解析】(1)t;(5-2t)(0≤t≤2.5)或(2t-5)(2.5提示:∵四边形ABCD是矩形,∴∠B=90°,
∴AC===5(cm).
由题意得AE=CF=t cm.
当0≤t≤2.5时,
EF=AC-AE-CF=(5-2t)cm;
当2.5(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∴∠GAF=∠HCE.
∵G,H分别是AB,DC的中点,∴AG=CH.
∵AE=CF,∴AE+EF=CF+EF,即AF=CE.
在△AFG与△CEH中,
∴△AFG≌△CEH,∴GF=HE.
在△AGE与△CHF中,
∴△AGE≌△CHF,∴GE=HF,
∴四边形EGFH是平行四边形.
(3)如图,连接GH.
由(2)知四边形EGFH是平行四边形.
∵G,H分别是矩形ABCD的边AB,DC的中点,
∴GH=BC=4 cm,
∴当EF=GH=4 cm时,四边形EGFH是矩形.
分两种情况:
①当0≤t≤2.5时,EF=(5-2t)cm,即5-2t=4,解得t=0.5.
②当2.5即2t-5=4,解得t=4.5.
综上所述,当t=0.5或4.5时,四边形EGFH为矩形.
2
【练基础】
必备知识1 有一个角是直角的平行四边形是矩形
1.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
2.如图,在 ABCD中,点E,F在AD边上,且BF=CE,AE=DF.
(1)求证:△ABF≌△DCE.
(2)求证:四边形ABCD是矩形.
必备知识2 对角线相等的平行四边形是矩形
3.【邯郸期末】四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AC=BD B.∠ABD=∠CBD C.AB=BD D.AB=CD
4.如图,在 ABCD中,E为DC的中点,连接AE并延长交BC的延长线于点F,连接AC,DF.
(1)求证:AD=CF.
(2)嘉琪说:“添加一个条件,能使四边形ACFD是矩形”,你是否同意嘉琪的观点 如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
必备知识3 有三个角是直角的四边形是矩形
5.如图,在△ABC中,AB=AC,AE⊥BC于点E,AD平分∠FAC,CD⊥AD于点D.求证:四边形AECD是矩形.
6.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE,DF分别是△BDC,△ADC的角平分线.
(1)求∠CFD的度数.
(2)求证:四边形FDEC是矩形.
【练能力】
7.【教材P68T9变式】如图,连接四边形ABCD各边中点得到四边形EFGH,还要添加_______才能使四边形EFGH是矩形.(写出一个条件即可,图中不能再添加别的“点”或“线”)
8.如图,在 ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF.
(2)设=k,当k为何值时,四边形DEBF是矩形 请说明理由.
9.如图,已知点M,O,N在同一直线上,OB,OC分别是∠AOM与∠AON的平分线,AB⊥OB,AC⊥OC,垂足分别为B,C,连接BC交AO于点E.
(1)求证:四边形ACOB是矩形.
(2)猜想BC与MN的位置关系,并证明你的结论.
10.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形.
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长.
【练素养】
11.如图,在矩形ABCD中,AB=3 cm,BC=4 cm,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1 cm/s,运动时间为t s,0≤t≤5.
(1)AE=________ cm,EF=________ cm.(用含t的式子表示)
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)的条件下,当t为何值时,四边形EGFH为矩形.
参考答案
【练基础】
1.C
2.【证明】(1)∵四边形ABCD是平行四边形,∴AB=CD.
∵AE=FD,∴AE+EF=FD+EF,即AF=DE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SSS).
(2)由(1)可知△ABF≌△DCE,∴∠A=∠D.
∵四边形ABCD是平行四边形,∴∠A+∠D=180°,∴2∠A=180°,∴∠A=90°,∴ ABCD是矩形.
3.A
4.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠CFE,∠ADE=∠FCE.
∵E为DC的中点,∴ED=EC,
∴△ADE≌△FCE(AAS),∴AD=CF.
(2)同意.当DC=AF时,四边形ACFD是矩形.
证明:∵AD∥CF,AD=CF,∴四边形ACFD是平行四边形.
∵DC=AF,∴四边形ACFD是矩形.
5.【证明】∵AB=AC,AE⊥BC于点E,
∴∠AEC=90°,∠BAE=∠CAE=∠BAC.
∵AD平分∠FAC,∴∠DAC=∠FAC,
∴∠DAE=∠DAC+∠CAE=∠BAC+∠FAC=(∠BAC+∠FAC)=×180°=90°.
又∵CD⊥AD于点D,∴∠ADC=90°,∴四边形AECD是矩形.
6.【解析】(1)∵∠ACB=90°,D是AB的中点,
∴BD=CD=AD.
∵DF是∠ADC的平分线,∴DF⊥AC.
∴∠CFD=90°.
(2)证明:∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD.
∵DE是∠BDC的平分线,∴DE⊥BC,
∴∠DEC=90°.
∵∠CFD=90°,∠ACB=90°,
∴四边形DECF是矩形.
【练能力】
7.AC⊥BD(答案不唯一)
8.【解析】(1)证明:解法一 如图,连接DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=OC.
∵E,F分别为AO,OC的中点,
∴EO=OA,OF=OC,
∴EO=FO.
∵BO=OD,EO=FO,
∴四边形BFDE是平行四边形,
∴BE=DF.
解法二 ∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,∴∠DCF=∠BAE.
∵E,F分别OA,OC的中点,
∴AE=OA,CF=OC,∴AE=CF.
在△DCF和△BAE中,
∴△DCF≌△BAE,∴BE=DF.
(2)当k=2时,四边形DEBF是矩形.理由如下:
易知四边形DEBF是平行四边形,
当BD=EF,即OD=OE时,四边形DEBF是矩形,
此时AE=OE,∴AO=2OE,则k====2,
∴当k=2时,四边形DEBF是矩形.
9.【解析】(1)证明:∵OB,OC分别是∠AOM与∠AON的平分线,
∴∠AOM=2∠AOB,∠AON=2∠AOC.
∵点M,O,N在同一直线上,∴∠AOM+∠AON=180°,
∴2∠AOB+2∠AOC=180°,∴∠AOB+∠AOC=90°,即∠BOC=90°.
∵AB⊥OB,AC⊥OC,∴∠ABO=∠ACO=90°,∴四边形ACOB是矩形.
(2)BC∥MN.证明:由(1)可得,四边形ACOB是矩形,∴OE=CE,
∴∠AOC=∠BCO.
∵OC是∠AON的平分线,∴∠AOC=∠NOC,
∴∠BCO=∠NOC,∴BC∥MN.
10.【解析】(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵CF=AE,∴DF=BE.
又∵DC∥AB,∴四边形DFBE是平行四边形,
∵DE⊥AB,∴平行四边形BFDE是矩形.
(2)∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=,DE==.
由(1)可得四边形DFBE是矩形,
∴BF=DE=.
∵AF平分∠DAB,∴∠FAB=∠DAB=30°,且BF⊥AB,
∴AF=2BF=3,
∴AB==,∴CD=.
【练素养】
11.【解析】(1)t;(5-2t)(0≤t≤2.5)或(2t-5)(2.5
∴AC===5(cm).
由题意得AE=CF=t cm.
当0≤t≤2.5时,
EF=AC-AE-CF=(5-2t)cm;
当2.5
∴AB=CD,AB∥CD,∴∠GAF=∠HCE.
∵G,H分别是AB,DC的中点,∴AG=CH.
∵AE=CF,∴AE+EF=CF+EF,即AF=CE.
在△AFG与△CEH中,
∴△AFG≌△CEH,∴GF=HE.
在△AGE与△CHF中,
∴△AGE≌△CHF,∴GE=HF,
∴四边形EGFH是平行四边形.
(3)如图,连接GH.
由(2)知四边形EGFH是平行四边形.
∵G,H分别是矩形ABCD的边AB,DC的中点,
∴GH=BC=4 cm,
∴当EF=GH=4 cm时,四边形EGFH是矩形.
分两种情况:
①当0≤t≤2.5时,EF=(5-2t)cm,即5-2t=4,解得t=0.5.
②当2.5
综上所述,当t=0.5或4.5时,四边形EGFH为矩形.
2
