2023-2024学年初中数学人教版八年级下册18.2.2.2 菱形的判定 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册18.2.2.2 菱形的判定 课时练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览


文档简介
18.2.2.2 菱形的判定
【练基础】
必备知识1 有一组邻边相等的平行四边形是菱形
1.已知平行四边形ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为菱形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DAC C.∠BAC=∠ABD D.∠BAC=∠ADB
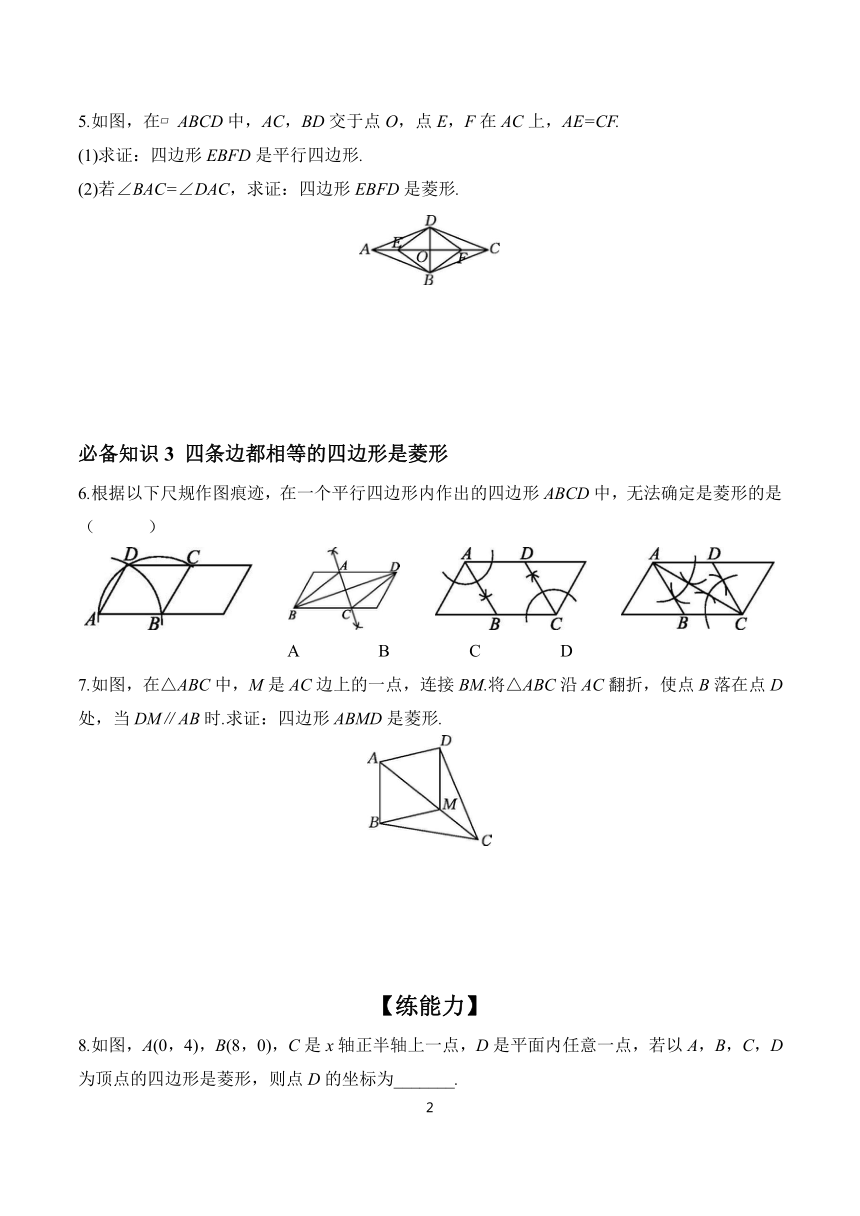
2.如图,∠ACB=90°,D为AB的中点,BE∥CD,CE∥AB.求证:四边形CEBD是菱形.
必备知识2 对角线互相垂直的平行四边形是菱形
3.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,则下列条件能判定四边形ABCD为菱形的是( )
A.AB=CD B.OA=OC,OB=OD C.AC=BD D.AB∥CD,AD=BC
4.如图,在 ABCD中,E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是_______.
5.如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
必备知识3 四条边都相等的四边形是菱形
6.根据以下尺规作图痕迹,在一个平行四边形内作出的四边形ABCD中,无法确定是菱形的是( )
A B C D
7.如图,在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时.求证:四边形ABMD是菱形.
【练能力】
8.如图,A(0,4),B(8,0),C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_______.
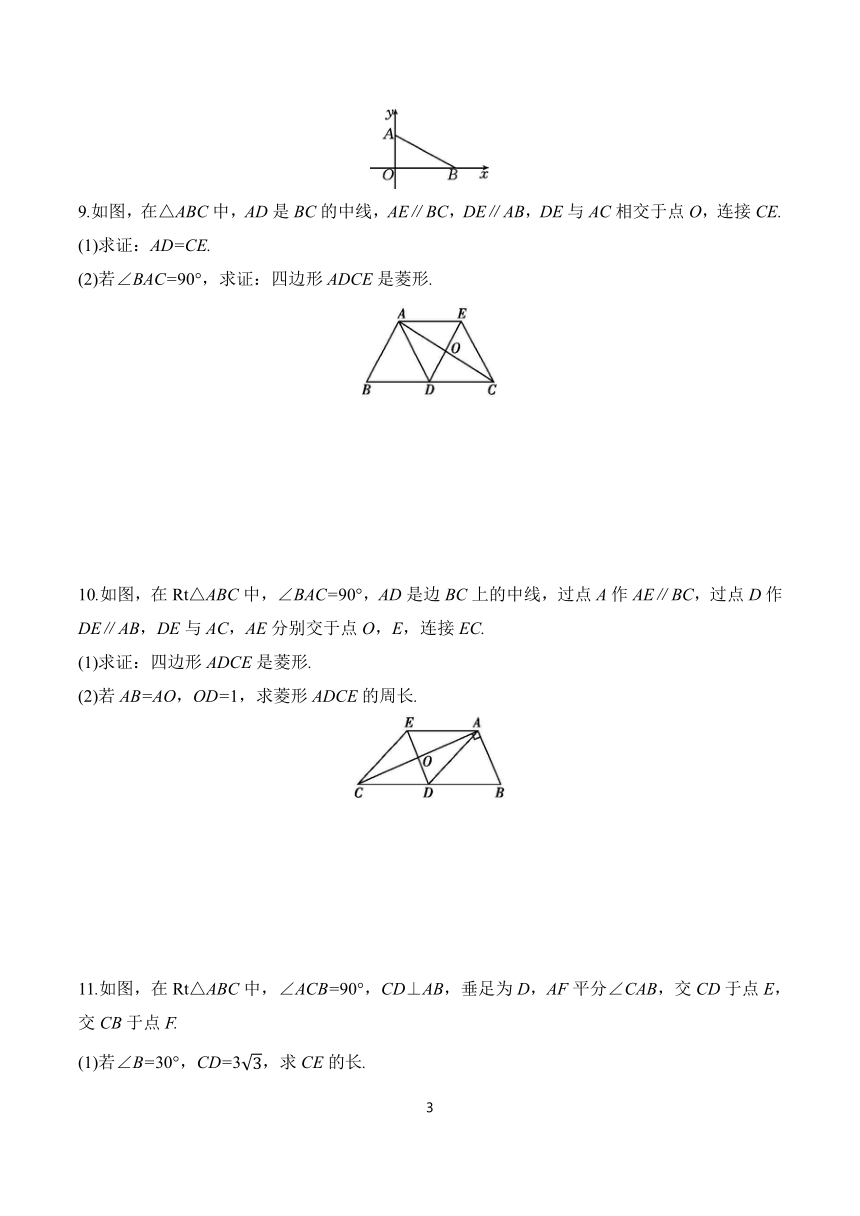
9.如图,在△ABC中,AD是BC的中线,AE∥BC,DE∥AB,DE与AC相交于点O,连接CE.
(1)求证:AD=CE.
(2)若∠BAC=90°,求证:四边形ADCE是菱形.
10.如图,在Rt△ABC中,∠BAC=90°,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC,AE分别交于点O,E,连接EC.
(1)求证:四边形ADCE是菱形.
(2)若AB=AO,OD=1,求菱形ADCE的周长.
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,CD=3,求CE的长.
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明理由.
【练素养】
12.(核心素养·运算能力)如图,在Rt△ABC中,∠B=90°,AC=40 cm,∠A=60°,点D从点C出发沿CA方向以2 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以1 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a(0(1)四边形AEFD能够成为菱形吗 如果能,求出相应的a值;如果不能,请说明理由.
(2)当a为何值时,△DEF为直角三角形 请说明理由.
参考答案
【练基础】
1.B
2.【证明】∵BE∥CD,CE∥AB,
∴四边形CEBD是平行四边形.
∵∠ACB=90°,D为AB的中点,
∴CD=AB=BD,
∴平行四边形CEBD是菱形.
3.B 4.BD⊥EF
5.【证明】(1)在 ABCD中,OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
∴四边形EBFD是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,∴∠BAC=∠DCA.
解法一 ∵∠BAC=∠DAC,
∴∠DCA=∠DAC,∴DA=DC.
∵OA=OC,∴DB⊥EF,
∴平行四边形EBFD是菱形.
解法二 ∵∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴DA=DC,
∴ ABCD为菱形,
∴AC⊥BD,
∴DB⊥EF,∴平行四边形EBFD是菱形.
6.C
7.【证明】∵DM∥AB,∴∠BAM=∠AMD.
∵△ADC是由△ABC沿AC翻折得到的,
∴∠CAB=∠CAD,AB=AD,BM=DM,
∴∠DAM=∠AMD,∴AD=DM,
∴AD=DM=AB=BM,
∴四边形ABMD是菱形.
【练能力】
8.(5,4)或(4,4) 【解析】①当AB为菱形的对角线时,
如图1,设菱形的边长为m,
∵A(0,4),B(8,0),∴OA=4,OB=8.
∵四边形ACBD为菱形,∴CA=AD=BC=m,AD∥BC.
在Rt△AOC中,由勾股定理,得42+(8-m)2=m2,解得m=5,∴D(5,4).
②当AB为菱形的边时,如图2,AB==4.
∵四边形ABCD为菱形,∴BC=AB=AD=4.
∵AD∥BC,
∴D(4,4).
综上所述,点D的坐标为(5,4)或(4,4).
9.【证明】(1)∵DE∥AB,AE∥BC,∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD.
∵AD是BC的中线,∴BD=CD,∴AE=CD.
∵AE∥CD,∴四边形ADCE是平行四边形,
∴AD=CE.
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD.
由(1)得四边形ADCE是平行四边形,
∴平行四边形ADCE是菱形.
10.【解析】(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE为平行四边形,∴AE=BD.
∵AD是边BC上的中线,∴BD=CD,∴AE=CD,
∴四边形ADCE是平行四边形.
又∵∠BAC=90°,AD是边BC上的中线,
∴AD=BC=CD,
∴平行四边形ADCE是菱形.
(2)∵四边形ADCE是菱形,
∴AD=AE=CE=CD,AC⊥DE,OA=OC.
∵BD=CD,∴OD是△ABC的中位线,
∴AB=2OD=2,∴AO=AB=2.
∴AD===,
∴菱形ADCE的周长=4AD=4.
11.【解析】(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°.
∵CD⊥AB,∴∠ADC=90°,
∴∠ACD=30°.
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE.
∵DE=AE,∴DE=CE,
∴CD=CE+DE=CE+CE,
∴CE=3,∴CE=2.
(2)四边形CEGF是菱形.
理由:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF.
在Rt△ACF与Rt△AGF中,AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG.
∵CD⊥AB,FG⊥AB,
∴CD∥FG,∴∠CEF=∠EFG,
∴∠CEF=∠CFE,∴CE=CF,∴CE=FG.
又∵CE∥FG,
∴四边形CEGF是平行四边形.
∵CE=CF,
∴平行四边形CEGF是菱形.
【练素养】
12.【解析】(1)能.
在△DFC中,∠DFC=90°,∠C=30°,DC=2a,
∴DF=a.
∵AE=a,∴AE=DF.
∵AB⊥BC,DF⊥BC,∴AE∥DF.
∴四边形AEFD为平行四边形,当AE=AD时,四边形AEFD为菱形,
即40-2a=a,解得a=,∴当a=时,四边形AEFD为菱形.
(2)当a=16或10时,△DEF为直角三角形.
理由:①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,
∴EF∥AD,∴∠ADE=∠DEF=90°.
∵∠A=60°,∴∠AED=30°,∴AD=AE=a.
又∵AD=40-2a,∴40-2a=a,解得a=16;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中,∠A=60°,则∠ADE=30°,
∴AD=2AE,即40-2a=2a,解得a=10;
③若∠EFD=90°,则点E与点B重合,点D与点A重合,此种情况不存在.
综上所述,当a=16或10时,△DEF为直角三角形.
2
【练基础】
必备知识1 有一组邻边相等的平行四边形是菱形
1.已知平行四边形ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为菱形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DAC C.∠BAC=∠ABD D.∠BAC=∠ADB
2.如图,∠ACB=90°,D为AB的中点,BE∥CD,CE∥AB.求证:四边形CEBD是菱形.
必备知识2 对角线互相垂直的平行四边形是菱形
3.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,则下列条件能判定四边形ABCD为菱形的是( )
A.AB=CD B.OA=OC,OB=OD C.AC=BD D.AB∥CD,AD=BC
4.如图,在 ABCD中,E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是_______.
5.如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
必备知识3 四条边都相等的四边形是菱形
6.根据以下尺规作图痕迹,在一个平行四边形内作出的四边形ABCD中,无法确定是菱形的是( )
A B C D
7.如图,在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时.求证:四边形ABMD是菱形.
【练能力】
8.如图,A(0,4),B(8,0),C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_______.
9.如图,在△ABC中,AD是BC的中线,AE∥BC,DE∥AB,DE与AC相交于点O,连接CE.
(1)求证:AD=CE.
(2)若∠BAC=90°,求证:四边形ADCE是菱形.
10.如图,在Rt△ABC中,∠BAC=90°,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC,AE分别交于点O,E,连接EC.
(1)求证:四边形ADCE是菱形.
(2)若AB=AO,OD=1,求菱形ADCE的周长.
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,CD=3,求CE的长.
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明理由.
【练素养】
12.(核心素养·运算能力)如图,在Rt△ABC中,∠B=90°,AC=40 cm,∠A=60°,点D从点C出发沿CA方向以2 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以1 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a(0
(2)当a为何值时,△DEF为直角三角形 请说明理由.
参考答案
【练基础】
1.B
2.【证明】∵BE∥CD,CE∥AB,
∴四边形CEBD是平行四边形.
∵∠ACB=90°,D为AB的中点,
∴CD=AB=BD,
∴平行四边形CEBD是菱形.
3.B 4.BD⊥EF
5.【证明】(1)在 ABCD中,OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
∴四边形EBFD是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,∴∠BAC=∠DCA.
解法一 ∵∠BAC=∠DAC,
∴∠DCA=∠DAC,∴DA=DC.
∵OA=OC,∴DB⊥EF,
∴平行四边形EBFD是菱形.
解法二 ∵∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴DA=DC,
∴ ABCD为菱形,
∴AC⊥BD,
∴DB⊥EF,∴平行四边形EBFD是菱形.
6.C
7.【证明】∵DM∥AB,∴∠BAM=∠AMD.
∵△ADC是由△ABC沿AC翻折得到的,
∴∠CAB=∠CAD,AB=AD,BM=DM,
∴∠DAM=∠AMD,∴AD=DM,
∴AD=DM=AB=BM,
∴四边形ABMD是菱形.
【练能力】
8.(5,4)或(4,4) 【解析】①当AB为菱形的对角线时,
如图1,设菱形的边长为m,
∵A(0,4),B(8,0),∴OA=4,OB=8.
∵四边形ACBD为菱形,∴CA=AD=BC=m,AD∥BC.
在Rt△AOC中,由勾股定理,得42+(8-m)2=m2,解得m=5,∴D(5,4).
②当AB为菱形的边时,如图2,AB==4.
∵四边形ABCD为菱形,∴BC=AB=AD=4.
∵AD∥BC,
∴D(4,4).
综上所述,点D的坐标为(5,4)或(4,4).
9.【证明】(1)∵DE∥AB,AE∥BC,∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD.
∵AD是BC的中线,∴BD=CD,∴AE=CD.
∵AE∥CD,∴四边形ADCE是平行四边形,
∴AD=CE.
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD.
由(1)得四边形ADCE是平行四边形,
∴平行四边形ADCE是菱形.
10.【解析】(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE为平行四边形,∴AE=BD.
∵AD是边BC上的中线,∴BD=CD,∴AE=CD,
∴四边形ADCE是平行四边形.
又∵∠BAC=90°,AD是边BC上的中线,
∴AD=BC=CD,
∴平行四边形ADCE是菱形.
(2)∵四边形ADCE是菱形,
∴AD=AE=CE=CD,AC⊥DE,OA=OC.
∵BD=CD,∴OD是△ABC的中位线,
∴AB=2OD=2,∴AO=AB=2.
∴AD===,
∴菱形ADCE的周长=4AD=4.
11.【解析】(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°.
∵CD⊥AB,∴∠ADC=90°,
∴∠ACD=30°.
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE.
∵DE=AE,∴DE=CE,
∴CD=CE+DE=CE+CE,
∴CE=3,∴CE=2.
(2)四边形CEGF是菱形.
理由:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF.
在Rt△ACF与Rt△AGF中,AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG.
∵CD⊥AB,FG⊥AB,
∴CD∥FG,∴∠CEF=∠EFG,
∴∠CEF=∠CFE,∴CE=CF,∴CE=FG.
又∵CE∥FG,
∴四边形CEGF是平行四边形.
∵CE=CF,
∴平行四边形CEGF是菱形.
【练素养】
12.【解析】(1)能.
在△DFC中,∠DFC=90°,∠C=30°,DC=2a,
∴DF=a.
∵AE=a,∴AE=DF.
∵AB⊥BC,DF⊥BC,∴AE∥DF.
∴四边形AEFD为平行四边形,当AE=AD时,四边形AEFD为菱形,
即40-2a=a,解得a=,∴当a=时,四边形AEFD为菱形.
(2)当a=16或10时,△DEF为直角三角形.
理由:①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,
∴EF∥AD,∴∠ADE=∠DEF=90°.
∵∠A=60°,∴∠AED=30°,∴AD=AE=a.
又∵AD=40-2a,∴40-2a=a,解得a=16;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中,∠A=60°,则∠ADE=30°,
∴AD=2AE,即40-2a=2a,解得a=10;
③若∠EFD=90°,则点E与点B重合,点D与点A重合,此种情况不存在.
综上所述,当a=16或10时,△DEF为直角三角形.
2
