2023-2024学年初中数学人教版八年级下册19.2.5 一次函数解析式的求法 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册19.2.5 一次函数解析式的求法 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:21:00 | ||
图片预览


文档简介
19.2.5 一次函数解析式的求法
【练基础】
必备知识 用待定系数法求一次函数的解析式
1.【教材P93例4变式】已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
2.在平面直角坐标系中,点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是( )
A.-6 B.6 C.6或3 D.6或-6
3.已知一次函数y=kx+b的图象过点(0,5)与(2,3),则该一次函数的表达式为_______.
4.已知一次函数的图象过点(2,5)与(-3,-10).
(1)求这个一次函数的解析式.
(2)直接写出这个一次函数的图象与两坐标轴的交点坐标.
5.如图,一次函数的图象经过点P(4,2)和B(0,-2),与x轴交于点A.
(1)求一次函数的解析式.
(2)在x轴上存在一点Q,且△ABQ的面积为6,求点Q的坐标.
6.如图,直线AB过点A(-1,5),P(2,a),B(3,-3).
(1)求直线AB的函数解析式和a的值.
(2)直线AB分别与x轴、y轴交于点C,D,请求出点C,D的坐标.
(3)求△AOP的面积.
【练能力】
7.一次函数y=-3x+b的图象经过点A(-3,m),B(-1,n),则m,n满足的关系式是( )
A.m+n=6 B.m+n=-6 C.m-n=6 D.m-n=-6
8.已知一次函数y=mx-4m,当1≤x≤3时,2≤y≤6,则m的值为( )
A.3 B.2 C.-2 D.2或-2
9.如图,若把直线l向上平移2个单位长度得到直线l',则直线l'对应的函数解析式为( )
A.y=x+1 B.y=x-1 C.y=-x-1 D.y=-x+1
10.已知某直线经过点A(0,2),且与两坐标轴围成的三角形的面积为2,则该直线的解析式是_______.
11.如图,直线l1经过点A(0,2)和C(6,-2),点B的坐标为(4,2),P是线段AB上的动点(点P不与点A重合).直线l2:y=kx+2k经过点P,并与l1交于点M,过点P作PN⊥l2,交l1于点N.
(1)求l1的函数表达式.
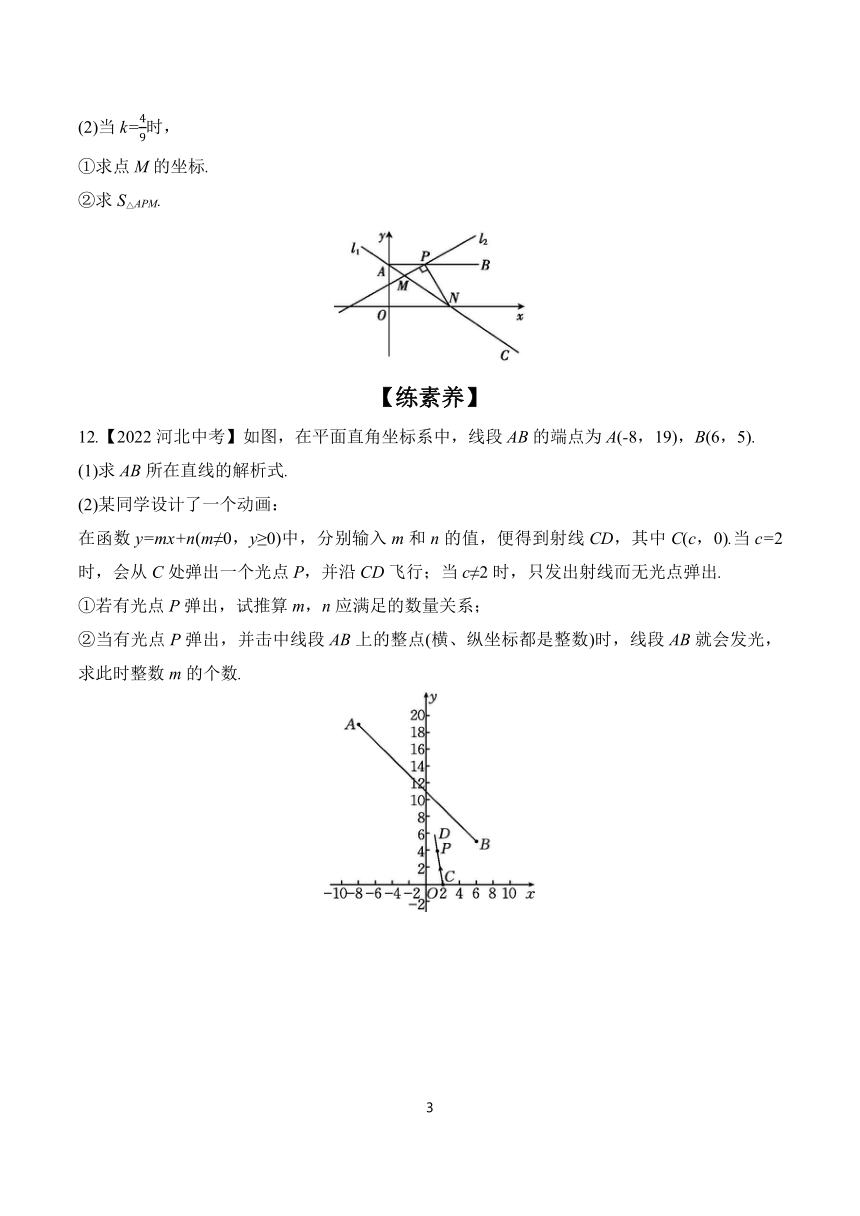
(2)当k=时,
①求点M的坐标.
②求S△APM.
【练素养】
12.【2022河北中考】如图,在平面直角坐标系中,线段AB的端点为A(-8,19),B(6,5).
(1)求AB所在直线的解析式.
(2)某同学设计了一个动画:
在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,便得到射线CD,其中C(c,0).当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.
①若有光点P弹出,试推算m,n应满足的数量关系;
②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.
参考答案
【练基础】
1.A 2.B 3.y=-x+5
4.【解析】(1)设一次函数解析式为y=kx+b,
把(2,5)与(-3,-10)代入上式,
得
解得
所以一次函数解析式为y=3x-1.
(2),0,(0,-1).
提示:当y=0时,3x-1=0,解得x=,
所以一次函数y=3x-1的图象与x轴的交点为,0.
当x=0时,×0-1=y,
解得y=-1,
所以一次函数y=3x-1的图象与y轴的交点为(0,-1).
5.【解析】(1)设一次函数解析式为y=kx+b,
把P(4,2)和B(0,-2)分别代入,
得解得
∴一次函数解析式为y=x-2.
(2)设点Q的坐标为(t,0),
当y=0时,x-2=0,解得x=2,
∴点A的坐标为(2,0).
∵△ABQ的面积为6,
∴×|t-2|×2=6,解得t=8或t=-4,
∴Q点的坐标为(-4,0)或(8,0).
6.【解析】(1)设直线AB解析式为y=kx+b.
将A(-1,5),B(3,-3)代入得
解得
∴直线AB的函数解析式为y=-2x+3,
把P(2,a)代入y=-2x+3,得a=-2×2+3=-1,
∴a的值是-1.
(2)在y=-2x+3中,令x=0,得y=3,
∴点D的坐标为(0,3).
在y=-2x+3中,令y=0得x=,
∴点C的坐标为,0.
(3)∵D(0,3),A(-1,5),P(2,-1),
∴S△AOD=×3×1=,S△POD=×3×2=3,
∴S△AOP=S△AOD+S△POD=,
∴△AOP的面积为.
【练能力】
7.C 8.C
9.D 【解析】解法一 设直线l对应的函数解析式为y=kx+b(k≠0).
观察题图,可知点(-2,0)和(0,-1)在直线l上,所以解得所以直线l对应的函数解析式为y=-x-1.
因为直线l'是直线l向上平移2个单位长度得到的,所以直线l'对应的函数解析式为y=-x-1+2=-x+1.
解法二 因为直线l经过第二、第四象限,且直线l'是由直线l平移得到的,所以直线l'经过第二、第四象限,排除选项A,B;因为直线l经过点(0,-1),所以向上平移2个单位长度后,直线l'经过点(0,1),排除选项C.
10.y=x+2或y=-x+2
【解析】设该直线的解析式为y=kx+b,把(0,2)代入,得b=2,所以y=kx+2,令y=0,得x=-.
因为直线与两坐标轴围成的三角形的面积为2,所以×2×-=2,解得k=1或-1,所以所求的直线的解析式为y=x+2或y=-x+2.
11.【解析】(1)设l1的函数表达式为y=k1x+b,
将点A(0,2)和C(6,-2)代入,
得
解得
∴l1的表达式为y=-x+2.
(2)①当k=时,
l2的表达式为y=x+,
联立l1,l2,
得
解得
则交点M的坐标为1,.
②当y=2时,有2=x+,
解得x=,∴P点坐标为,2,
∴点M到直线AP的距离是2-=,
∴S△APM=××=.
【练素养】
12.【解析】(1)设AB所在直线的解析式为y=kx+b,
把A(-8,19),B(6,5)的坐标代入,
得解得
∴AB所在直线的解析式为y=-x+11.
(2)①由题意知,若有光点P弹出,则直线y=mx+n经过点(2,0),
∴2m+n=0.
②解法一 设光点P击中线段AB上的点为(a,d),则d=-a+11,
∴a=11-d(5≤d≤19),当d是整数时,a也是整数.
∵点P在y=mx+n上,
∴由①得d=ma-2m,
∴m===-1,
只有d=6,8,10,12,18时,m为整数,且其个数是5.
解法二 ∵线段AB上的整数点有15个:(-8,19),(-7,18),(-6,17),(-5,16),(-4,15),(-3,14),(-2,13),(-1,12),(0,11),(1,10),(2,9),(3,8),(4,7),(5,6),(6,5).
当射线CD经过点(2,0),(-7,18)时,得y=-2x+4,此时m=-2,符合题意;
当射线CD经过点(2,0),(-1,12)时,得y=-4x+8,此时m=-4,符合题意;
当射线CD经过点(2,0),(1,10)时,得y=-10x+20,此时m=-10,符合题意;
当射线CD经过点(2,0),(3,8)时,得y=8x-16,此时m=8,符合题意;
当射线CD经过点(2,0),(5,6)时,得y=2x-4,此时m=2,符合题意.
其他点都不符合题意.
综上所述,符合题意的整数m的值有5个.
2
【练基础】
必备知识 用待定系数法求一次函数的解析式
1.【教材P93例4变式】已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
2.在平面直角坐标系中,点A(2,-3),B(4,3),C(5,a)在同一条直线上,则a的值是( )
A.-6 B.6 C.6或3 D.6或-6
3.已知一次函数y=kx+b的图象过点(0,5)与(2,3),则该一次函数的表达式为_______.
4.已知一次函数的图象过点(2,5)与(-3,-10).
(1)求这个一次函数的解析式.
(2)直接写出这个一次函数的图象与两坐标轴的交点坐标.
5.如图,一次函数的图象经过点P(4,2)和B(0,-2),与x轴交于点A.
(1)求一次函数的解析式.
(2)在x轴上存在一点Q,且△ABQ的面积为6,求点Q的坐标.
6.如图,直线AB过点A(-1,5),P(2,a),B(3,-3).
(1)求直线AB的函数解析式和a的值.
(2)直线AB分别与x轴、y轴交于点C,D,请求出点C,D的坐标.
(3)求△AOP的面积.
【练能力】
7.一次函数y=-3x+b的图象经过点A(-3,m),B(-1,n),则m,n满足的关系式是( )
A.m+n=6 B.m+n=-6 C.m-n=6 D.m-n=-6
8.已知一次函数y=mx-4m,当1≤x≤3时,2≤y≤6,则m的值为( )
A.3 B.2 C.-2 D.2或-2
9.如图,若把直线l向上平移2个单位长度得到直线l',则直线l'对应的函数解析式为( )
A.y=x+1 B.y=x-1 C.y=-x-1 D.y=-x+1
10.已知某直线经过点A(0,2),且与两坐标轴围成的三角形的面积为2,则该直线的解析式是_______.
11.如图,直线l1经过点A(0,2)和C(6,-2),点B的坐标为(4,2),P是线段AB上的动点(点P不与点A重合).直线l2:y=kx+2k经过点P,并与l1交于点M,过点P作PN⊥l2,交l1于点N.
(1)求l1的函数表达式.
(2)当k=时,
①求点M的坐标.
②求S△APM.
【练素养】
12.【2022河北中考】如图,在平面直角坐标系中,线段AB的端点为A(-8,19),B(6,5).
(1)求AB所在直线的解析式.
(2)某同学设计了一个动画:
在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,便得到射线CD,其中C(c,0).当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.
①若有光点P弹出,试推算m,n应满足的数量关系;
②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.
参考答案
【练基础】
1.A 2.B 3.y=-x+5
4.【解析】(1)设一次函数解析式为y=kx+b,
把(2,5)与(-3,-10)代入上式,
得
解得
所以一次函数解析式为y=3x-1.
(2),0,(0,-1).
提示:当y=0时,3x-1=0,解得x=,
所以一次函数y=3x-1的图象与x轴的交点为,0.
当x=0时,×0-1=y,
解得y=-1,
所以一次函数y=3x-1的图象与y轴的交点为(0,-1).
5.【解析】(1)设一次函数解析式为y=kx+b,
把P(4,2)和B(0,-2)分别代入,
得解得
∴一次函数解析式为y=x-2.
(2)设点Q的坐标为(t,0),
当y=0时,x-2=0,解得x=2,
∴点A的坐标为(2,0).
∵△ABQ的面积为6,
∴×|t-2|×2=6,解得t=8或t=-4,
∴Q点的坐标为(-4,0)或(8,0).
6.【解析】(1)设直线AB解析式为y=kx+b.
将A(-1,5),B(3,-3)代入得
解得
∴直线AB的函数解析式为y=-2x+3,
把P(2,a)代入y=-2x+3,得a=-2×2+3=-1,
∴a的值是-1.
(2)在y=-2x+3中,令x=0,得y=3,
∴点D的坐标为(0,3).
在y=-2x+3中,令y=0得x=,
∴点C的坐标为,0.
(3)∵D(0,3),A(-1,5),P(2,-1),
∴S△AOD=×3×1=,S△POD=×3×2=3,
∴S△AOP=S△AOD+S△POD=,
∴△AOP的面积为.
【练能力】
7.C 8.C
9.D 【解析】解法一 设直线l对应的函数解析式为y=kx+b(k≠0).
观察题图,可知点(-2,0)和(0,-1)在直线l上,所以解得所以直线l对应的函数解析式为y=-x-1.
因为直线l'是直线l向上平移2个单位长度得到的,所以直线l'对应的函数解析式为y=-x-1+2=-x+1.
解法二 因为直线l经过第二、第四象限,且直线l'是由直线l平移得到的,所以直线l'经过第二、第四象限,排除选项A,B;因为直线l经过点(0,-1),所以向上平移2个单位长度后,直线l'经过点(0,1),排除选项C.
10.y=x+2或y=-x+2
【解析】设该直线的解析式为y=kx+b,把(0,2)代入,得b=2,所以y=kx+2,令y=0,得x=-.
因为直线与两坐标轴围成的三角形的面积为2,所以×2×-=2,解得k=1或-1,所以所求的直线的解析式为y=x+2或y=-x+2.
11.【解析】(1)设l1的函数表达式为y=k1x+b,
将点A(0,2)和C(6,-2)代入,
得
解得
∴l1的表达式为y=-x+2.
(2)①当k=时,
l2的表达式为y=x+,
联立l1,l2,
得
解得
则交点M的坐标为1,.
②当y=2时,有2=x+,
解得x=,∴P点坐标为,2,
∴点M到直线AP的距离是2-=,
∴S△APM=××=.
【练素养】
12.【解析】(1)设AB所在直线的解析式为y=kx+b,
把A(-8,19),B(6,5)的坐标代入,
得解得
∴AB所在直线的解析式为y=-x+11.
(2)①由题意知,若有光点P弹出,则直线y=mx+n经过点(2,0),
∴2m+n=0.
②解法一 设光点P击中线段AB上的点为(a,d),则d=-a+11,
∴a=11-d(5≤d≤19),当d是整数时,a也是整数.
∵点P在y=mx+n上,
∴由①得d=ma-2m,
∴m===-1,
只有d=6,8,10,12,18时,m为整数,且其个数是5.
解法二 ∵线段AB上的整数点有15个:(-8,19),(-7,18),(-6,17),(-5,16),(-4,15),(-3,14),(-2,13),(-1,12),(0,11),(1,10),(2,9),(3,8),(4,7),(5,6),(6,5).
当射线CD经过点(2,0),(-7,18)时,得y=-2x+4,此时m=-2,符合题意;
当射线CD经过点(2,0),(-1,12)时,得y=-4x+8,此时m=-4,符合题意;
当射线CD经过点(2,0),(1,10)时,得y=-10x+20,此时m=-10,符合题意;
当射线CD经过点(2,0),(3,8)时,得y=8x-16,此时m=8,符合题意;
当射线CD经过点(2,0),(5,6)时,得y=2x-4,此时m=2,符合题意.
其他点都不符合题意.
综上所述,符合题意的整数m的值有5个.
2
