2023-2024学年初中数学人教版八年级下册19.2.6 一次函数的应用 课时练习(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册19.2.6 一次函数的应用 课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 85.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 12:21:40 | ||
图片预览


文档简介
19.2.6 一次函数的应用
【练基础】
必备知识 利用一次函数解决实际问题
1.【2021安徽中考】某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系.若22码鞋子的长度为16 cm,44码鞋子的长度为27 cm,则38码鞋子的长度为( )
A.23 cm B.24 cm C.25 cm D.26 cm
2.一辆汽车油箱中剩余的油量y(L)与已行驶的路程x(km)的对应关系如图所示.如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为( )
A.150 km B.165 km C.125 km D.350 km
3.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最新人体构造学的研究成果,一般情况下人的指距d和身高h成某种关系.下表是测得的指距与身高的一组数据:
身高h/cm 160 169 178 187
指距d/cm 20 21 22 23
根据上表解决下面这个实际问题:某人的身高是205 cm,可预测他的指距为( )
A.28 cm B.27 cm C.26 cm D.25 cm
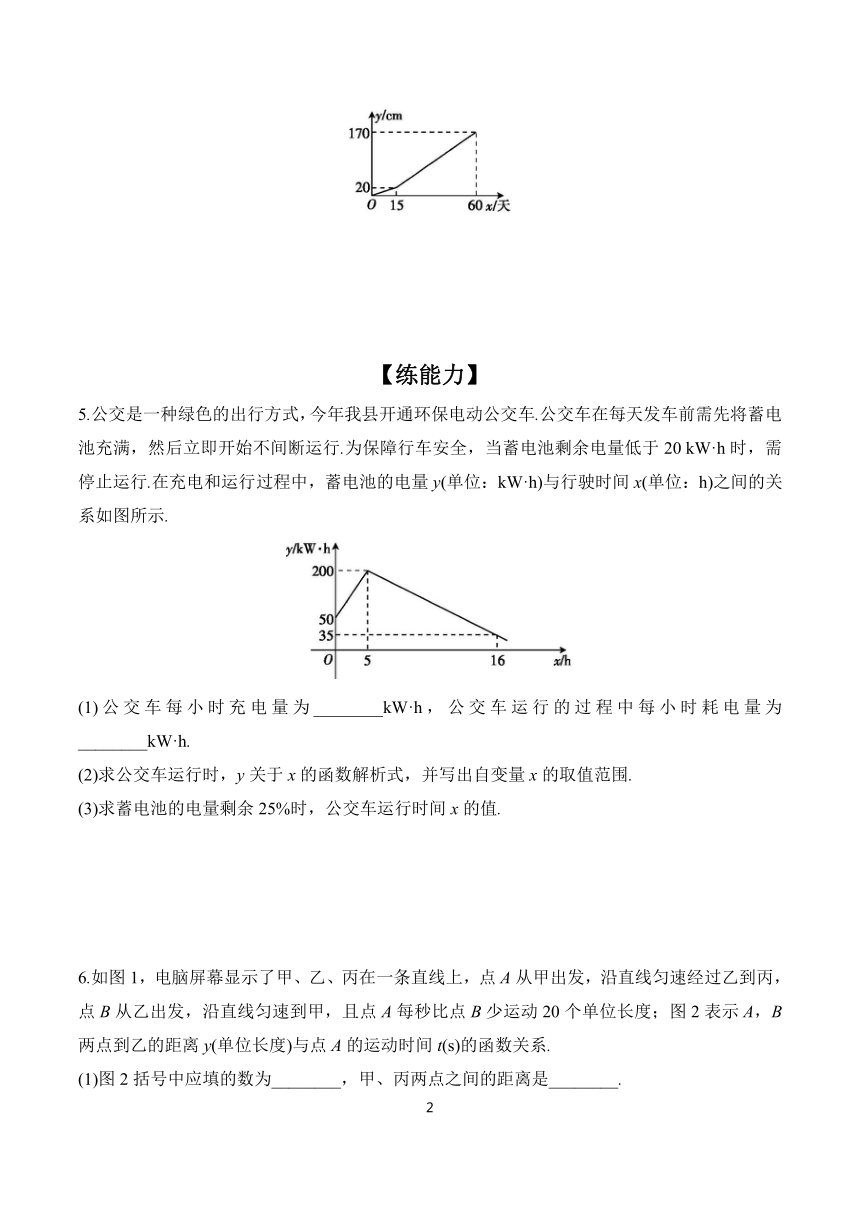
4.一农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20 cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式.
(2)当这种瓜苗长到大约90 cm时,才开始开花结果,试问这种瓜苗移至大棚后,继续生长大约多少天,才开始开花结果
【练能力】
5.公交是一种绿色的出行方式,今年我县开通环保电动公交车.公交车在每天发车前需先将蓄电池充满,然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于20 kW·h时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:kW·h)与行驶时间x(单位:h)之间的关系如图所示.
(1)公交车每小时充电量为________kW·h,公交车运行的过程中每小时耗电量为________kW·h.
(2)求公交车运行时,y关于x的函数解析式,并写出自变量x的取值范围.
(3)求蓄电池的电量剩余25%时,公交车运行时间x的值.
6.如图1,电脑屏幕显示了甲、乙、丙在一条直线上,点A从甲出发,沿直线匀速经过乙到丙,点B从乙出发,沿直线匀速到甲,且点A每秒比点B少运动20个单位长度;图2表示A,B两点到乙的距离y(单位长度)与点A的运动时间t(s)的函数关系.
(1)图2括号中应填的数为________,甲、丙两点之间的距离是________.
(2)求直线MN的函数关系式.
(3)已知A,B两点均在运动,若A,B两点到乙的距离和为300个单位长度,求t的值.
【练素养】
7.如图,小强组装了一款遥控车,并在长度为160 m的跑道AB上试验它在不同速度下的运行情况.从点A出发,先以2 m/s的速度行进了20 s,接着以4 m/s的速度行进到终点B,为记录,全程安装了拍摄设备,拍摄设备在与起点A距离40 m处的P点.设遥控车的运动时间为x(s),遥控车与拍摄点的距离为y(m).
(1)求y与x之间的函数关系式并写出x的取值范围.
(2)求遥控车距离拍摄点10 m时的运动时间.
(3)当遥控车从点A出发时,一个机器人从拍摄点出发以a m/s的速度向点B行进,并在与点B相离20 m内(不与点B重合)被遥控车追上,直接写出a的取值范围.
参考答案
【练基础】
1.B
2.A 【解析】解法一 设剩余的油量y(L)与已行驶的路程x(km)之间的函数解析式为y=kx+b,由题图可知,函数图象经过点(500,0),(0,50),所以所以所以函数解析式为y=-x+50,所以当y=35时,x=150.
解法二 由题意可知,汽车的耗油量为50÷500=0.1(L/km),所以当油箱中剩余的油量为35 L时,该汽车已行驶的路程为(50-35)÷0.1=150(km).
3.D
4.【解析】(1)当0≤x≤15时,设y=kx(k≠0),
则20=15k,解得k=,∴y=x.
当15则解得
∴y=x-30,
∴y=
(2)当y=90时,90=x-30,解得x=36,
36-15=21(天).
答:这种瓜苗移至大棚后,继续生长大约21天,开始开花结果.
【练能力】
5.【解析】(1)由图象知,5 h共充电200-50=150 kW·h,
∴每小时充电量为150÷5=30 kW·h.
由图象知,11 h共耗电200-35=165 kW·h,
∴公交车运行的过程中每小时耗电量为165÷11=15 kW·h.
故答案为30;15.
(2)设公交车运行时y关于x的函数解析式为y=kx+b,图象经过点(5,200)和(16,35),将其代入,得解得
∴y=-15x+275.
当y=20时,x=17,
∴5≤x≤17,
∴公交车运行时,y关于x的函数解析式为y=-15x+275(5≤x≤17).
(3)当蓄电池的电量剩余25%时,y=25%×200=50,
将y=50代入解析式中得50=-15x+275,
解得x=15,
∴公交车运行时间x的值为15.
6.【解析】(1)由图象可知,点A的速度为480÷8=60(单位长度/s),
∴点B的速度为60+20=80(单位长度/s),
∴点B运动到甲所需的时间为480÷80=6(s),
∴括号中应填的数为4+6=10,
∴甲、丙两点之间的距离是10×60=600(单位长度),
故答案为10;600.
(2)设直线MN的函数关系式为y=kt+b,
将M(4,0),N(10,480)代入,得
解得
∴直线MN的函数关系式为y=80t-320.
(3)当点B未出发时,即0解得t=3.
当点B出发后,点A还未到乙地时,即4解得t=7.
当点A在乙和丙之间时,即8解得t=7(此时A不在乙和丙之间,舍去).
综上所述,t的值为3或7.
【练素养】
7.【解析】(1)当0≤x≤20时,y=40-2x=-2x+40,
遥控车从P点到B点所用时间为(160-40)÷4=30(s),
当20综上所述,y=
(2)将y=10代入y=-2x+40得,
10=-2x+40,
解得x=15.
将x=10代入y=4x-80得,10=4x-80,解得x=22.5,
∴当遥控车距离拍摄点10 m时的运动时间为15 s或22.5 s.
(3)遥控车走到距离B点20米处所用时间为20+(160-40-20)÷4=20+25=45(s),
遥控车走到B点所用时间为20+(160-40)÷4=20+30=50(s),
遥控车在距离B点20米内追上机器人,则45a>100,且50a<120,解得故a的取值范围为2
【练基础】
必备知识 利用一次函数解决实际问题
1.【2021安徽中考】某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系.若22码鞋子的长度为16 cm,44码鞋子的长度为27 cm,则38码鞋子的长度为( )
A.23 cm B.24 cm C.25 cm D.26 cm
2.一辆汽车油箱中剩余的油量y(L)与已行驶的路程x(km)的对应关系如图所示.如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为( )
A.150 km B.165 km C.125 km D.350 km
3.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最新人体构造学的研究成果,一般情况下人的指距d和身高h成某种关系.下表是测得的指距与身高的一组数据:
身高h/cm 160 169 178 187
指距d/cm 20 21 22 23
根据上表解决下面这个实际问题:某人的身高是205 cm,可预测他的指距为( )
A.28 cm B.27 cm C.26 cm D.25 cm
4.一农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20 cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式.
(2)当这种瓜苗长到大约90 cm时,才开始开花结果,试问这种瓜苗移至大棚后,继续生长大约多少天,才开始开花结果
【练能力】
5.公交是一种绿色的出行方式,今年我县开通环保电动公交车.公交车在每天发车前需先将蓄电池充满,然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于20 kW·h时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:kW·h)与行驶时间x(单位:h)之间的关系如图所示.
(1)公交车每小时充电量为________kW·h,公交车运行的过程中每小时耗电量为________kW·h.
(2)求公交车运行时,y关于x的函数解析式,并写出自变量x的取值范围.
(3)求蓄电池的电量剩余25%时,公交车运行时间x的值.
6.如图1,电脑屏幕显示了甲、乙、丙在一条直线上,点A从甲出发,沿直线匀速经过乙到丙,点B从乙出发,沿直线匀速到甲,且点A每秒比点B少运动20个单位长度;图2表示A,B两点到乙的距离y(单位长度)与点A的运动时间t(s)的函数关系.
(1)图2括号中应填的数为________,甲、丙两点之间的距离是________.
(2)求直线MN的函数关系式.
(3)已知A,B两点均在运动,若A,B两点到乙的距离和为300个单位长度,求t的值.
【练素养】
7.如图,小强组装了一款遥控车,并在长度为160 m的跑道AB上试验它在不同速度下的运行情况.从点A出发,先以2 m/s的速度行进了20 s,接着以4 m/s的速度行进到终点B,为记录,全程安装了拍摄设备,拍摄设备在与起点A距离40 m处的P点.设遥控车的运动时间为x(s),遥控车与拍摄点的距离为y(m).
(1)求y与x之间的函数关系式并写出x的取值范围.
(2)求遥控车距离拍摄点10 m时的运动时间.
(3)当遥控车从点A出发时,一个机器人从拍摄点出发以a m/s的速度向点B行进,并在与点B相离20 m内(不与点B重合)被遥控车追上,直接写出a的取值范围.
参考答案
【练基础】
1.B
2.A 【解析】解法一 设剩余的油量y(L)与已行驶的路程x(km)之间的函数解析式为y=kx+b,由题图可知,函数图象经过点(500,0),(0,50),所以所以所以函数解析式为y=-x+50,所以当y=35时,x=150.
解法二 由题意可知,汽车的耗油量为50÷500=0.1(L/km),所以当油箱中剩余的油量为35 L时,该汽车已行驶的路程为(50-35)÷0.1=150(km).
3.D
4.【解析】(1)当0≤x≤15时,设y=kx(k≠0),
则20=15k,解得k=,∴y=x.
当15
∴y=x-30,
∴y=
(2)当y=90时,90=x-30,解得x=36,
36-15=21(天).
答:这种瓜苗移至大棚后,继续生长大约21天,开始开花结果.
【练能力】
5.【解析】(1)由图象知,5 h共充电200-50=150 kW·h,
∴每小时充电量为150÷5=30 kW·h.
由图象知,11 h共耗电200-35=165 kW·h,
∴公交车运行的过程中每小时耗电量为165÷11=15 kW·h.
故答案为30;15.
(2)设公交车运行时y关于x的函数解析式为y=kx+b,图象经过点(5,200)和(16,35),将其代入,得解得
∴y=-15x+275.
当y=20时,x=17,
∴5≤x≤17,
∴公交车运行时,y关于x的函数解析式为y=-15x+275(5≤x≤17).
(3)当蓄电池的电量剩余25%时,y=25%×200=50,
将y=50代入解析式中得50=-15x+275,
解得x=15,
∴公交车运行时间x的值为15.
6.【解析】(1)由图象可知,点A的速度为480÷8=60(单位长度/s),
∴点B的速度为60+20=80(单位长度/s),
∴点B运动到甲所需的时间为480÷80=6(s),
∴括号中应填的数为4+6=10,
∴甲、丙两点之间的距离是10×60=600(单位长度),
故答案为10;600.
(2)设直线MN的函数关系式为y=kt+b,
将M(4,0),N(10,480)代入,得
解得
∴直线MN的函数关系式为y=80t-320.
(3)当点B未出发时,即0
当点B出发后,点A还未到乙地时,即4
当点A在乙和丙之间时,即8
综上所述,t的值为3或7.
【练素养】
7.【解析】(1)当0≤x≤20时,y=40-2x=-2x+40,
遥控车从P点到B点所用时间为(160-40)÷4=30(s),
当20
(2)将y=10代入y=-2x+40得,
10=-2x+40,
解得x=15.
将x=10代入y=4x-80得,10=4x-80,解得x=22.5,
∴当遥控车距离拍摄点10 m时的运动时间为15 s或22.5 s.
(3)遥控车走到距离B点20米处所用时间为20+(160-40-20)÷4=20+25=45(s),
遥控车走到B点所用时间为20+(160-40)÷4=20+30=50(s),
遥控车在距离B点20米内追上机器人,则45a>100,且50a<120,解得
