2.1 锐角三角函数 课件(共23张PPT) 2023--2024学年鲁教版(五四制)数学八年级上册
文档属性
| 名称 | 2.1 锐角三角函数 课件(共23张PPT) 2023--2024学年鲁教版(五四制)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 25.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 14:19:29 | ||
图片预览








文档简介
(共23张PPT)
第二章 直角三角形的边角关系
2.1 锐角三角函数
第1课时 正切
创设情境
创设情境
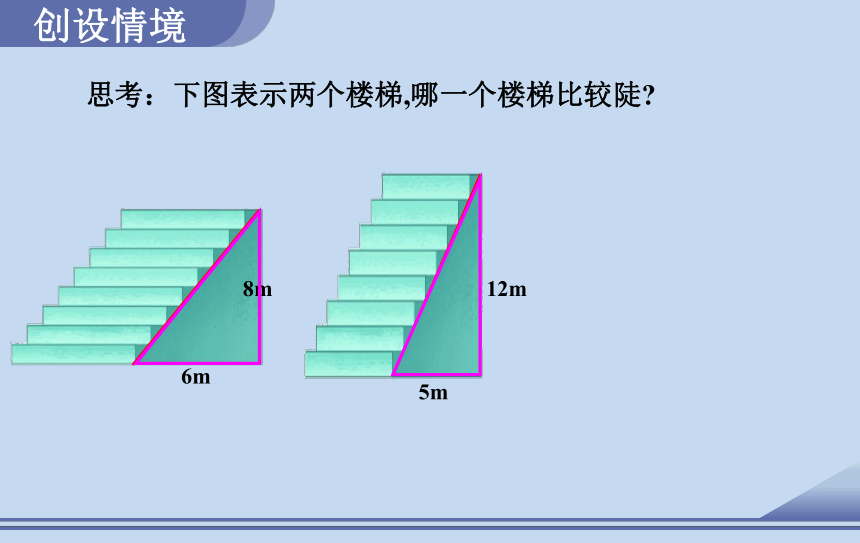
5m
12m
6m
8m
思考:下图表示两个楼梯,哪一个楼梯比较陡
1
2
3
4
A
C
B
边与边的关系:
勾股定理(a2+b2=c2)
角与角的关系:在直角三角形中,两锐角互余。(∠A+∠B=90°)
特殊边角关系:
在直角三角形中,30°角所对的直角边是斜边的一半。
直角三角形的边角关系 ?
大单元理念
学习目标
体会数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题。
能够用正切表示直角三角形两边之比
并进行简单的计算。
理解锐角三角函数正切的含义,会用正切值来判断梯子或斜坡的陡与缓。
更深一步地理解数学来源于生活,服务于生活。
实验过程:用三角形学具模拟梯子,进行数学探究,比较所给梯子的倾斜程度,完成实验报告单上的4组实验。越大——梯子越陡
实验工具:三角形学具、直尺、三角尺
实验思考:
在比较过程中,发现什么量决定梯子的倾斜程度?
梯子越陡
数学实验室
小组分工要求:
1.小组成员中一人负责测量角度;
2.小组成员中一人负责测量梯子的铅直高和水平宽;
3.小组成员中一人负责计算梯子的铅直高与水平宽的比值;
4.小组成员中一人负责实验报告的填写。
4
2
E
F
D
4
3
B
A
C
如图,梯子AB和EF哪个更陡?你是怎样判断的?
4
2
E
F
D
3
2
A
B
C
数学实验室
实验出真知
3
6
D
E
F
C
2
B
4
A
2
5
A
B
C
3
6
D
E
F
数学实验室
1
2
3
4
5
6
7
8
A
C
B
铅直高
水平宽
数学实验室
倾斜角越大—梯子越陡
铅直高度与水平宽度的比值越大—梯子越陡
小明想利用前面探究的结论解决实际问题,他想测量图中梯子的倾斜程度,因为点B1 太高,不宜测量铅直高,所以他选择测量点B2的铅直高和水平宽来计算梯子的倾斜程度,你同意他的观点吗?
合作探究
B2
C2
A
C1
B1
1.Rt△AB1C1和Rt△AB2C2有什么关系?
B3
B2
C2
C3
A
C1
B1
合作探究
2. 和 有什么关系?
3.如果改变B2C2在梯子上的位置(如B3C3), 和 有什么关系?
在直角三角形中,当锐角不变时,其对边与邻边的比值也不变。
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
tanA=
∠A的对边
∠A的邻边
三角
函数
构建新知
火眼金睛
1. 如图(1),在△ABC中, ( )
2. 如图(2),在Rt△ABC中, ( )
3. 如图(2),在Rt△ABC中, ( )
4. 如图(2),在Rt△ABC中, ( )
5. 如图(2),在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值也扩大100倍。 ( )
温馨提示
跟踪训练
1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。
变式训练
A
B
C
┌
2.如图,在△ABC中,∠C=90°,AC=6, tanB= ,
则BC=________
变式1:如图,△ABC中,∠C=90°,AC=6, tanB= ,
则AB=________
变式2:如图,△ABC中,∠C=90°,AB=10, tanB= ,
则AC=________
变式3:如图,在△ABC中,AB=AC=10, BC=16,
则tanB=________
A
B
C
D
变式训练
A
B
C
┌
3.如图,在△ ABC中,AC=6,BC=8,CD⊥AB于点D,
则tan∠ACD=____________
变式:如图,在△ ABC中,AC=6,BC=8,CD是斜边AB上的中线,则tan∠ACD=____________
D
D
解决问题
5m
12m
6m
8m
下图表示两个楼梯,哪一个楼梯比较陡
α
β
乙
甲
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
正切通常也用来描述山坡的坡度.
坡度越大,坡角越大,坡面就越陡.
学以致用
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的高度h和水平长度l的比称 为坡度i(或坡比),
即坡度等于坡角的正切.
i=(坡度通常写成h∶l的形式).
i==tanα
归纳:坡度越大,坡角越大,坡面就越陡.
A
B
C
生活数学
某人从山脚下的A处走了100米到达山顶的B处,已知点B到山脚A处的垂直高度BC为60米,则这个山坡的坡度为________。
跟踪训练
B
A
C
┌
掌握了……方法
设想锐角三角函数还可以从…角度进行研究
学会了……知识
体会了……思想
核心
素养
感悟收获
必做题:习题2.1第1、2题;
选做题:习题2.1第3题。
作业布置
A
C
B
铅直高度
水平宽度
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
梯子与地面的夹角∠ABC称为
倾斜角
数学实验室
相关概念:
第二章 直角三角形的边角关系
2.1 锐角三角函数
第1课时 正切
创设情境
创设情境
5m
12m
6m
8m
思考:下图表示两个楼梯,哪一个楼梯比较陡
1
2
3
4
A
C
B
边与边的关系:
勾股定理(a2+b2=c2)
角与角的关系:在直角三角形中,两锐角互余。(∠A+∠B=90°)
特殊边角关系:
在直角三角形中,30°角所对的直角边是斜边的一半。
直角三角形的边角关系 ?
大单元理念
学习目标
体会数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题。
能够用正切表示直角三角形两边之比
并进行简单的计算。
理解锐角三角函数正切的含义,会用正切值来判断梯子或斜坡的陡与缓。
更深一步地理解数学来源于生活,服务于生活。
实验过程:用三角形学具模拟梯子,进行数学探究,比较所给梯子的倾斜程度,完成实验报告单上的4组实验。越大——梯子越陡
实验工具:三角形学具、直尺、三角尺
实验思考:
在比较过程中,发现什么量决定梯子的倾斜程度?
梯子越陡
数学实验室
小组分工要求:
1.小组成员中一人负责测量角度;
2.小组成员中一人负责测量梯子的铅直高和水平宽;
3.小组成员中一人负责计算梯子的铅直高与水平宽的比值;
4.小组成员中一人负责实验报告的填写。
4
2
E
F
D
4
3
B
A
C
如图,梯子AB和EF哪个更陡?你是怎样判断的?
4
2
E
F
D
3
2
A
B
C
数学实验室
实验出真知
3
6
D
E
F
C
2
B
4
A
2
5
A
B
C
3
6
D
E
F
数学实验室
1
2
3
4
5
6
7
8
A
C
B
铅直高
水平宽
数学实验室
倾斜角越大—梯子越陡
铅直高度与水平宽度的比值越大—梯子越陡
小明想利用前面探究的结论解决实际问题,他想测量图中梯子的倾斜程度,因为点B1 太高,不宜测量铅直高,所以他选择测量点B2的铅直高和水平宽来计算梯子的倾斜程度,你同意他的观点吗?
合作探究
B2
C2
A
C1
B1
1.Rt△AB1C1和Rt△AB2C2有什么关系?
B3
B2
C2
C3
A
C1
B1
合作探究
2. 和 有什么关系?
3.如果改变B2C2在梯子上的位置(如B3C3), 和 有什么关系?
在直角三角形中,当锐角不变时,其对边与邻边的比值也不变。
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
tanA=
∠A的对边
∠A的邻边
三角
函数
构建新知
火眼金睛
1. 如图(1),在△ABC中, ( )
2. 如图(2),在Rt△ABC中, ( )
3. 如图(2),在Rt△ABC中, ( )
4. 如图(2),在Rt△ABC中, ( )
5. 如图(2),在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值也扩大100倍。 ( )
温馨提示
跟踪训练
1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。
变式训练
A
B
C
┌
2.如图,在△ABC中,∠C=90°,AC=6, tanB= ,
则BC=________
变式1:如图,△ABC中,∠C=90°,AC=6, tanB= ,
则AB=________
变式2:如图,△ABC中,∠C=90°,AB=10, tanB= ,
则AC=________
变式3:如图,在△ABC中,AB=AC=10, BC=16,
则tanB=________
A
B
C
D
变式训练
A
B
C
┌
3.如图,在△ ABC中,AC=6,BC=8,CD⊥AB于点D,
则tan∠ACD=____________
变式:如图,在△ ABC中,AC=6,BC=8,CD是斜边AB上的中线,则tan∠ACD=____________
D
D
解决问题
5m
12m
6m
8m
下图表示两个楼梯,哪一个楼梯比较陡
α
β
乙
甲
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
正切通常也用来描述山坡的坡度.
坡度越大,坡角越大,坡面就越陡.
学以致用
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的高度h和水平长度l的比称 为坡度i(或坡比),
即坡度等于坡角的正切.
i=(坡度通常写成h∶l的形式).
i==tanα
归纳:坡度越大,坡角越大,坡面就越陡.
A
B
C
生活数学
某人从山脚下的A处走了100米到达山顶的B处,已知点B到山脚A处的垂直高度BC为60米,则这个山坡的坡度为________。
跟踪训练
B
A
C
┌
掌握了……方法
设想锐角三角函数还可以从…角度进行研究
学会了……知识
体会了……思想
核心
素养
感悟收获
必做题:习题2.1第1、2题;
选做题:习题2.1第3题。
作业布置
A
C
B
铅直高度
水平宽度
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
梯子与地面的夹角∠ABC称为
倾斜角
数学实验室
相关概念:
