勾股定理的逆定理
图片预览




文档简介
课件15张PPT。18.2 勾股定理的逆定理(1) 勾股定理直角三角形中,两直角边的平方和等于斜边的平方. 如果 直角三角形的三边分别为a,b,c(c为斜边),
那么 a2 + b2=c2活动1 :复习 如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.据说,古埃及人曾用下面的方法画直角:做一做方法:
用剪刀剪出三条长度分别为:
(1) 5cm,12cm,13cm
(2) 9cm,15cm,12cm
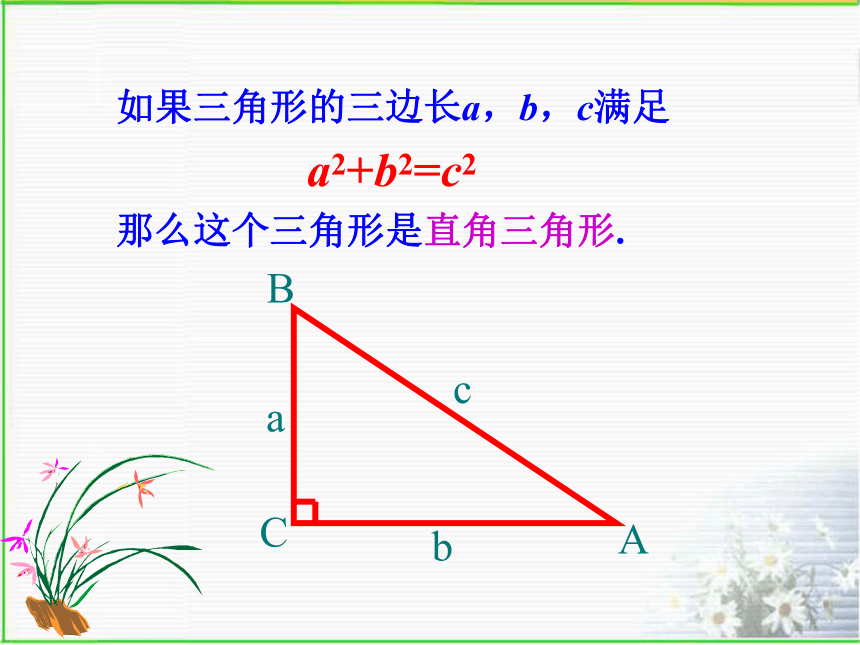
和你的同伴一起合作完成.你得到的是什么三角形?如果三角形的三边长a,b,c满足
a2+b2=c2
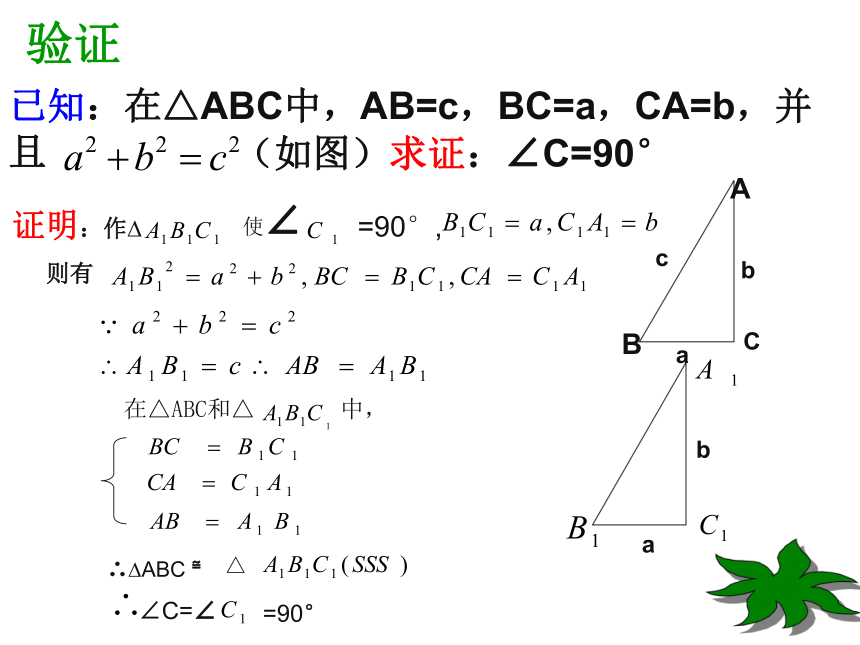
那么这个三角形是直角三角形.验证已知:在△ABC中,AB=c,BC=a,CA=b,并且 ABbc证明:作? ∠C=∠ Ca(如图)求证:∠C=90°使∠则有=90°=90°,比一比命题2 如果三角形的三边长a,b,c,满足
那么这个三角形是直角三角形.观察思考
(1)命题1和命题2的题设、结论分别是什么?它们有什么关系?
(2)你能否举出两个这种关系的命题? 我们把这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题. 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数. 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;说一说:BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形拓广与提高议一议1、如果三条线段长a、b、c满足 这三条线段组成的三角形是不是直角三角形?为什么? (1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的立方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
(5)对顶角相等 练:说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的立方相等,那么这两个实数相等. 成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立逆命题:相等的两个角是对顶角. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立注意:任何一个命题都有逆命题,但任何一个定理不一定有逆定理。 写出下列命题的逆命题并判断它们是否正确:
(1)直角三角形的两个锐角互余
练一练:(2)在直角三角形中, 如果有一个锐角是30°,那么它
所对的直角边是斜边的一半 ; (3)三内角之比为1:2:3的三角形为直角三角形
在直角三角形中, 如果一条直角边是斜边的一半,
那么它所对的锐角是30°; 直角三角形的三内角之比为1:2:3有两个锐角互余的三角形是直角三角形
1.通过本节课的学习,你收获了什么?
2. 判断一个三角形是否是直角三角形,都有哪些方法?课堂小结1、有一个角是直角的三角形
2、有两个锐角互余的三角形
3、勾股定理的逆定理
那么 a2 + b2=c2活动1 :复习 如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.据说,古埃及人曾用下面的方法画直角:做一做方法:
用剪刀剪出三条长度分别为:
(1) 5cm,12cm,13cm
(2) 9cm,15cm,12cm
和你的同伴一起合作完成.你得到的是什么三角形?如果三角形的三边长a,b,c满足
a2+b2=c2
那么这个三角形是直角三角形.验证已知:在△ABC中,AB=c,BC=a,CA=b,并且 ABbc证明:作? ∠C=∠ Ca(如图)求证:∠C=90°使∠则有=90°=90°,比一比命题2 如果三角形的三边长a,b,c,满足
那么这个三角形是直角三角形.观察思考
(1)命题1和命题2的题设、结论分别是什么?它们有什么关系?
(2)你能否举出两个这种关系的命题? 我们把这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题. 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数. 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;说一说:BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形拓广与提高议一议1、如果三条线段长a、b、c满足 这三条线段组成的三角形是不是直角三角形?为什么? (1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的立方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
(5)对顶角相等 练:说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的立方相等,那么这两个实数相等. 成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立逆命题:相等的两个角是对顶角. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立注意:任何一个命题都有逆命题,但任何一个定理不一定有逆定理。 写出下列命题的逆命题并判断它们是否正确:
(1)直角三角形的两个锐角互余
练一练:(2)在直角三角形中, 如果有一个锐角是30°,那么它
所对的直角边是斜边的一半 ; (3)三内角之比为1:2:3的三角形为直角三角形
在直角三角形中, 如果一条直角边是斜边的一半,
那么它所对的锐角是30°; 直角三角形的三内角之比为1:2:3有两个锐角互余的三角形是直角三角形
1.通过本节课的学习,你收获了什么?
2. 判断一个三角形是否是直角三角形,都有哪些方法?课堂小结1、有一个角是直角的三角形
2、有两个锐角互余的三角形
3、勾股定理的逆定理
