勾股定理的逆定理
图片预览



文档简介
课件15张PPT。18.2 勾股定理的逆定理(2)知识回顾勾股定理的逆定理:
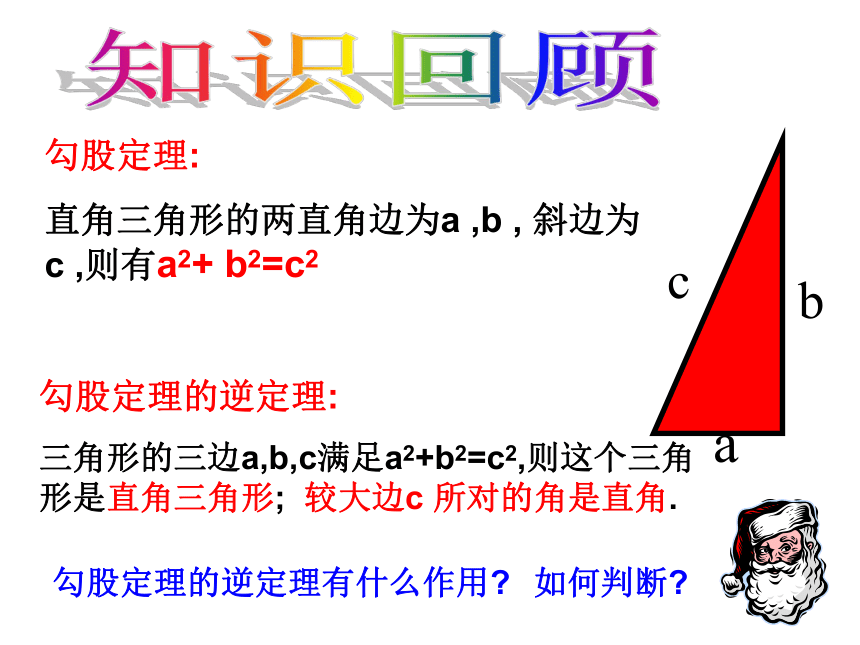
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.勾股定理:
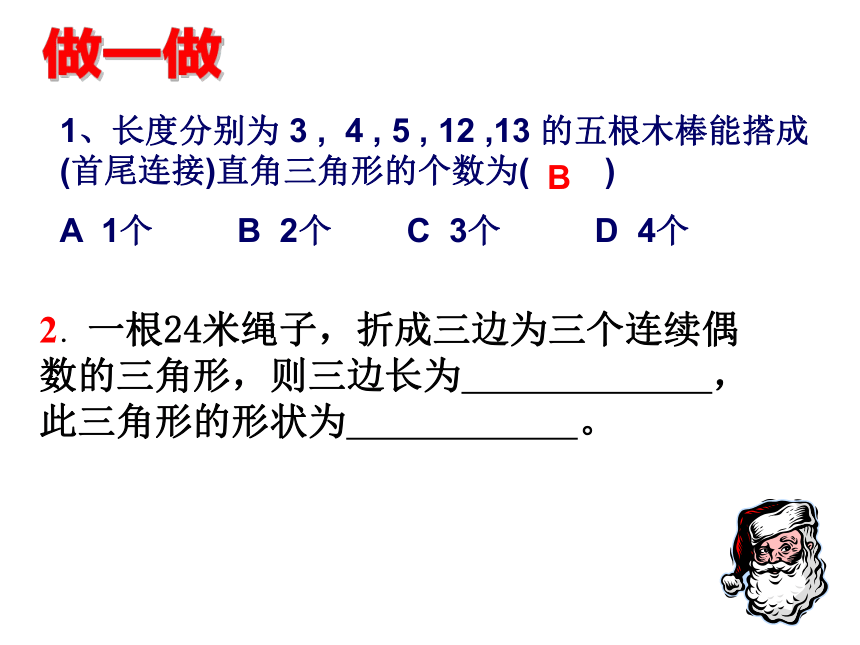
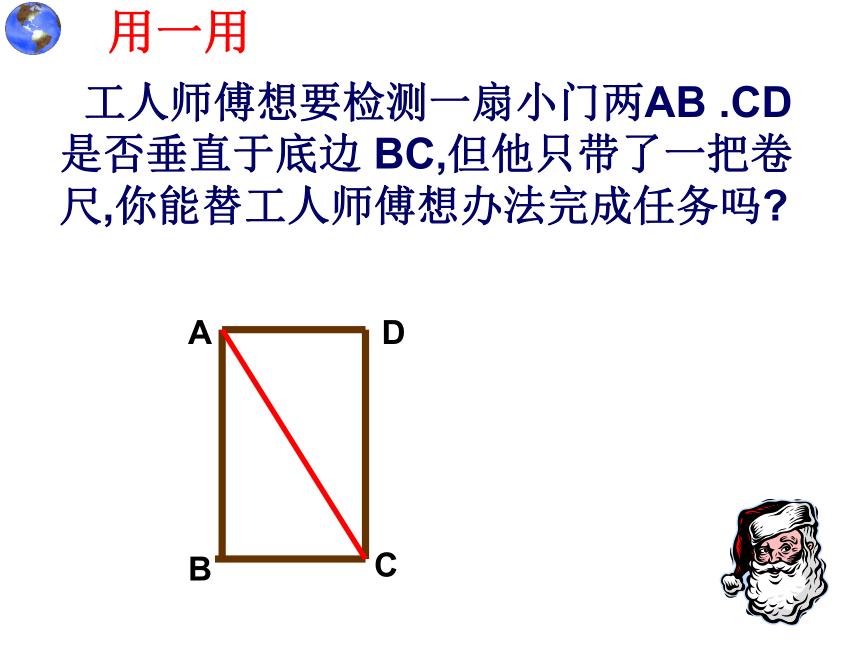
直角三角形的两直角边为a ,b , 斜边为 c ,则有a2+ b2=c2勾股定理的逆定理有什么作用?如何判断?做一做2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长为 ,此三角形的形状为 。1、长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个BA做一做思考 已知a.b.c为△ABC的三边,且满足
a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形例3 工人师傅想要检测一扇小门两AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗?用一用 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?应用举例解:根据题意画图,如图所示:PQ=16×1.5=24
PR=12×1.5=18
QR=30∵242+182=302,
即 PQ2+PR2=QR2∴∠QPR=900 由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.R’或东南方向 已知一个三角形三条边的长分别是16cm,12cm,20cm,求这个三角形最长边的高线长.综合应用CD=cm, AD=2cm, AC⊥AB。已知:在四边形ABCD中,AB=3cm, BC=5cm,求(1) S四边形ABCD(2)∠ DCA的度数例2∵AC⊥AB(已知)∴ AC2+AB2=BC2(勾股定理)∵ AB=3cm,BC=5cm又∵CD=2 cm AD=2cm(已知)∴ AC2=16 , CD2+AD2=12+4=16∴ AC2=CD2+AD2∴ ∠ADC=900(勾股定理的逆定理∴ S四边形ABCD=S △ ABC+ S△ ACD∴解(1)一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?6. 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
思维激活通过本节课的学习我巩固了哪些数学知识?我体会到了那些数学方法?课堂小结
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有a2+ b2=c2勾股定理的逆定理有什么作用?如何判断?做一做2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长为 ,此三角形的形状为 。1、长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个BA做一做思考 已知a.b.c为△ABC的三边,且满足
a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形例3 工人师傅想要检测一扇小门两AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗?用一用 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?应用举例解:根据题意画图,如图所示:PQ=16×1.5=24
PR=12×1.5=18
QR=30∵242+182=302,
即 PQ2+PR2=QR2∴∠QPR=900 由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.R’或东南方向 已知一个三角形三条边的长分别是16cm,12cm,20cm,求这个三角形最长边的高线长.综合应用CD=cm, AD=2cm, AC⊥AB。已知:在四边形ABCD中,AB=3cm, BC=5cm,求(1) S四边形ABCD(2)∠ DCA的度数例2∵AC⊥AB(已知)∴ AC2+AB2=BC2(勾股定理)∵ AB=3cm,BC=5cm又∵CD=2 cm AD=2cm(已知)∴ AC2=16 , CD2+AD2=12+4=16∴ AC2=CD2+AD2∴ ∠ADC=900(勾股定理的逆定理∴ S四边形ABCD=S △ ABC+ S△ ACD∴解(1)一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?6. 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
思维激活通过本节课的学习我巩固了哪些数学知识?我体会到了那些数学方法?课堂小结
