第六章 圆周运动 专题强化 圆周运动的传动问题和周期性问题 学案(学生版+教师版)—2024年春高中物理人教版必修二
文档属性
| 名称 | 第六章 圆周运动 专题强化 圆周运动的传动问题和周期性问题 学案(学生版+教师版)—2024年春高中物理人教版必修二 | 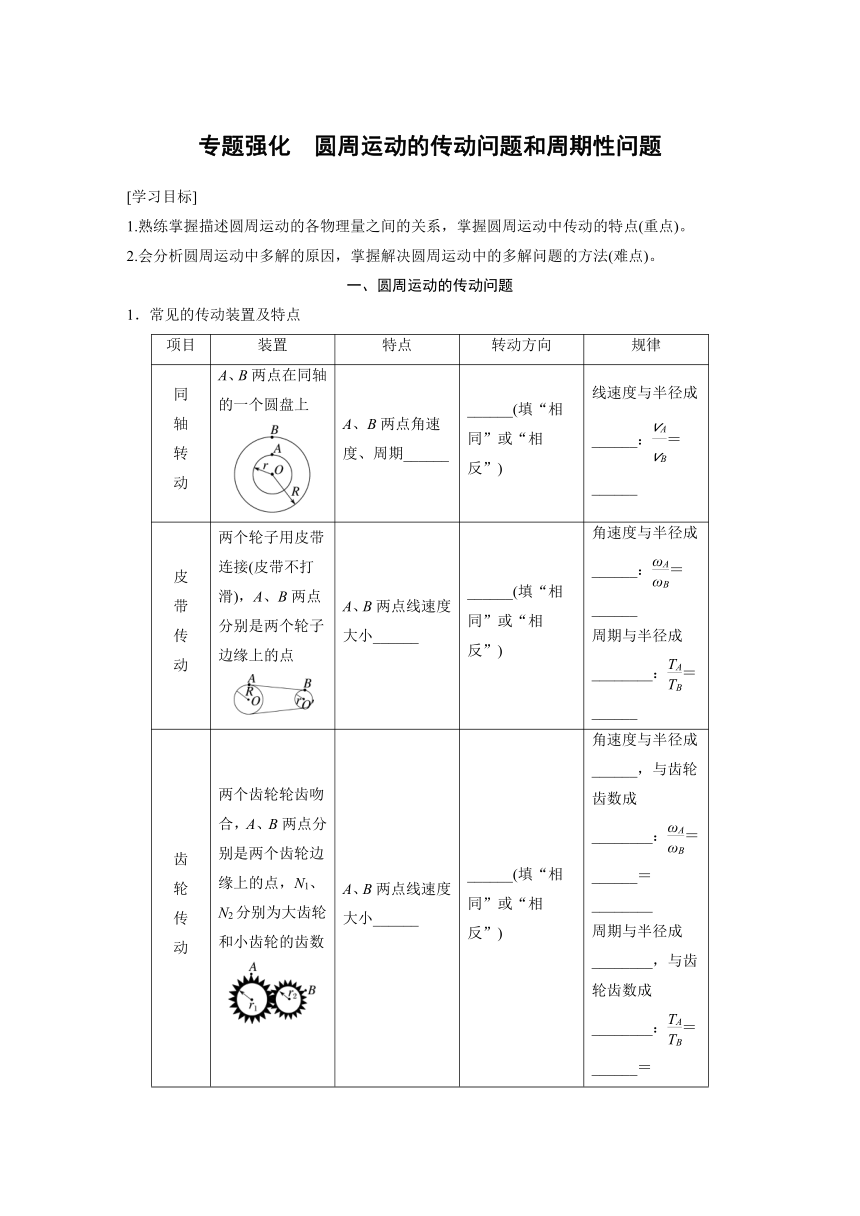 | |
| 格式 | docx | ||
| 文件大小 | 349.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-23 19:58:00 | ||
图片预览




文档简介
专题强化 圆周运动的传动问题和周期性问题
[学习目标]
1.熟练掌握描述圆周运动的各物理量之间的关系,掌握圆周运动中传动的特点(重点)。
2.会分析圆周运动中多解的原因,掌握解决圆周运动中的多解问题的方法(难点)。
一、圆周运动的传动问题
1.常见的传动装置及特点
项目 装置 特点 转动方向 规律
同 轴 转 动 A、B两点在同轴的一个圆盘上 A、B两点角速度、周期______ ______(填“相同”或“相反”) 线速度与半径成______:=______
皮 带 传 动 两个轮子用皮带连接(皮带不打滑),A、B两点分别是两个轮子边缘上的点 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______:=______ 周期与半径成________:=______
齿 轮 传 动 两个齿轮轮齿吻合,A、B两点分别是两个齿轮边缘上的点,N1、N2分别为大齿轮和小齿轮的齿数 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______,与齿轮齿数成________:=______=________ 周期与半径成________,与齿轮齿数成________:=______=________
摩 擦 传 动 两摩擦轮靠摩擦进行传动(两轮不打滑),A点和B点分别是两轮边缘上的点 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______:=______ 周期与半径成________:=______
2.求解传动问题的思路:
(1)分清传动特点:若属于皮带传动、齿轮传动或摩擦传动,则轮子边缘各点线速度大小相等;若属于同轴转动,则轮上各点的角速度相等。
(2)确定半径关系:根据装置中各点位置确定半径关系或根据题意确定半径关系。
(3)择式分析:若线速度大小相等,则根据ω∝分析;若角速度大小相等,则根据v∝r分析。
例1 如图所示,rA=3rB=3rC,则:
(1)vA∶vB=________,
ωA∶ωB=________。
(2)ωA∶ωC=________,
vA∶vC=________。
例2 如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1∶3,则在传动的过程中( )
A.甲、乙两轮的角速度之比为1∶3
B.甲、乙两轮的周期之比为3∶1
C.甲、乙两轮边缘处的线速度大小之比为3∶1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1
例3 自行车用链条传动来驱动后轮前进,如图是链条传动的示意图,两个齿轮俗称“牙盘”。A、B、C分别为牙盘边缘和后轮边缘上的点,大齿轮半径为r1、小齿轮半径为r2、后轮半径为r3。下列说法正确的是( )
A.A、B两点的角速度相等
B.B、C两点的线速度大小相等
C.大、小齿轮的转速之比为
D.在水平路面匀速骑行时,脚踏板转一圈,自行车前进的距离为2πr3
二、圆周运动的周期性和多解问题
如图所示,直径为d的纸质圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略子弹重力、圆筒的阻力及空气阻力。问:
(1)子弹做什么运动?圆筒做什么运动?
(2)为什么圆筒上只有一个弹孔?
(3)子弹与圆筒的运动时间有何关系?
(4)子弹的速度v应满足什么条件?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等)。
(3)运动的关系:两物体运动的时间______。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间______。
(2)先特殊后一般:先考虑一个周期的情况,再根据运动的________,考虑多个周期时的规律。
(3)分析时注意两个运动是________,互不影响。
例4 如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L=2 m,当飞镖以初速度v0=10 m/s垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动,忽略空气阻力,重力加速度为g=10 m/s2,若飞镖恰好击中P点,求:
(1)圆盘的半径;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(2)圆盘转动周期的可能值。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
专题强化 圆周运动的传动问题和周期性问题
[学习目标]
1.熟练掌握描述圆周运动的各物理量之间的关系,掌握圆周运动中传动的特点(重点)。
2.会分析圆周运动中多解的原因,掌握解决圆周运动中的多解问题的方法(难点)。
一、圆周运动的传动问题
1.常见的传动装置及特点
项目 装置 特点 转动方向 规律
同轴转动 A、B两点在同轴的一个圆盘上 A、B两点角速度、周期相同 相同(填“相同”或“相反”) 线速度与半径成正比:=
皮带传动 两个轮子用皮带连接(皮带不打滑),A、B两点分别是两个轮子边缘上的点 A、B两点线速度大小相等 相同(填“相同”或“相反”) 角速度与半径成反比:= 周期与半径成正比:=
齿轮传动 两个齿轮轮齿吻合,A、B两点分别是两个齿轮边缘上的点,N1、N2分别为大齿轮和小齿轮的齿数 A、B两点线速度大小相等 相反(填“相同”或“相反”) 角速度与半径成反比,与齿轮齿数成反比:== 周期与半径成正比,与齿轮齿数成正比:==
摩擦传动 两摩擦轮靠摩擦进行传动(两轮不打滑),A点和B点分别是两轮边缘上的点 A、B两点线速度大小相等 相反(填“相同”或“相反”) 角速度与半径成反比:= 周期与半径成正比:=
2.求解传动问题的思路:
(1)分清传动特点:若属于皮带传动、齿轮传动或摩擦传动,则轮子边缘各点线速度大小相等;若属于同轴转动,则轮上各点的角速度相等。
(2)确定半径关系:根据装置中各点位置确定半径关系或根据题意确定半径关系。
(3)择式分析:若线速度大小相等,则根据ω∝分析;若角速度大小相等,则根据v∝r分析。
例1 如图所示,rA=3rB=3rC,则:
(1)vA∶vB= ,ωA∶ωB= 。
(2)ωA∶ωC= ,vA∶vC= 。
答案 (1)1∶1 1∶3 (2)1∶1 3∶1
例2 如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1∶3,则在传动的过程中( )
A.甲、乙两轮的角速度之比为1∶3
B.甲、乙两轮的周期之比为3∶1
C.甲、乙两轮边缘处的线速度大小之比为3∶1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1
答案 D
解析 齿轮传动中,两轮边缘的线速度大小相等,即线速度大小之比为1∶1,选项C错误;根据v=ωr,甲、乙两个轮子的半径之比为1∶3,故甲、乙两轮的角速度之比为ω1∶ω2=3∶1,选项A错误;周期T=,所以甲、乙两轮的周期之比T1∶T2=1∶3,选项B错误;根据线速度的定义v=可知,弧长Δs=vΔt,即甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1,选项D正确。
例3 自行车用链条传动来驱动后轮前进,如图是链条传动的示意图,两个齿轮俗称“牙
盘”。A、B、C分别为牙盘边缘和后轮边缘上的点,大齿轮半径为r1、小齿轮半径为r2、后轮半径为r3。下列说法正确的是( )
A.A、B两点的角速度相等
B.B、C两点的线速度大小相等
C.大、小齿轮的转速之比为
D.在水平路面匀速骑行时,脚踏板转一圈,自行车前进的距离为2πr3
答案 D
解析 A、B两点属于皮带传动,线速度大小相等,因为半径不同,所以角速度不相等,故A错误;B、C两点属于同轴转动,角速度相等,因为半径不同,所以线速度大小不相等,故B错误;转速之比为===,故C错误;脚踏板转动一圈,自行车前进的距离为s=×2πr3=2πr3,故D正确。
二、圆周运动的周期性和多解问题
如图所示,直径为d的纸质圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略子弹重力、圆筒的阻力及空气阻力。问:
(1)子弹做什么运动?圆筒做什么运动?
(2)为什么圆筒上只有一个弹孔?
(3)子弹与圆筒的运动时间有何关系?
(4)子弹的速度v应满足什么条件?
答案 (1)子弹做匀速直线运动,圆筒做匀速圆周运动。
(2)子弹进圆筒时打了一个孔,恰好从这个孔出去,在子弹穿过圆筒过程中,圆筒转过了半圈或整数圈加半圈。
(3)子弹穿过圆筒的时间与圆筒转过半圈或整数圈加半圆的时间相等。
(4)子弹穿过圆筒所用时间t=,圆筒转过的角度θ=2nπ+π(n=0,1,2…),而ω=,联立可得v=(n=0,1,2…)。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等)。
(3)运动的关系:两物体运动的时间相等。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间相等。
(2)先特殊后一般:先考虑一个周期的情况,再根据运动的周期性,考虑多个周期时的规律。
(3)分析时注意两个运动是独立的,互不影响。
例4 如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L=2 m,当飞镖以初速度v0=10 m/s垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动,忽略空气阻力,重力加速度为g=10 m/s2,若飞镖恰好击中P点,求:
(1)圆盘的半径;
(2)圆盘转动周期的可能值。
答案 见解析
解析 (1)根据题意可知,飞镖做平抛运动,水平方向上有L=v0t,解得飞行时间为t==0.2 s,
竖直方向上有2R=gt2,
解得R=0.1 m=10 cm,
(2)根据题意,设圆盘转动的周期为T,则有t=T+kT(k=0,1,2,3…)
解得:T=(k=0,1,2,3…)。
[学习目标]
1.熟练掌握描述圆周运动的各物理量之间的关系,掌握圆周运动中传动的特点(重点)。
2.会分析圆周运动中多解的原因,掌握解决圆周运动中的多解问题的方法(难点)。
一、圆周运动的传动问题
1.常见的传动装置及特点
项目 装置 特点 转动方向 规律
同 轴 转 动 A、B两点在同轴的一个圆盘上 A、B两点角速度、周期______ ______(填“相同”或“相反”) 线速度与半径成______:=______
皮 带 传 动 两个轮子用皮带连接(皮带不打滑),A、B两点分别是两个轮子边缘上的点 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______:=______ 周期与半径成________:=______
齿 轮 传 动 两个齿轮轮齿吻合,A、B两点分别是两个齿轮边缘上的点,N1、N2分别为大齿轮和小齿轮的齿数 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______,与齿轮齿数成________:=______=________ 周期与半径成________,与齿轮齿数成________:=______=________
摩 擦 传 动 两摩擦轮靠摩擦进行传动(两轮不打滑),A点和B点分别是两轮边缘上的点 A、B两点线速度大小______ ______(填“相同”或“相反”) 角速度与半径成______:=______ 周期与半径成________:=______
2.求解传动问题的思路:
(1)分清传动特点:若属于皮带传动、齿轮传动或摩擦传动,则轮子边缘各点线速度大小相等;若属于同轴转动,则轮上各点的角速度相等。
(2)确定半径关系:根据装置中各点位置确定半径关系或根据题意确定半径关系。
(3)择式分析:若线速度大小相等,则根据ω∝分析;若角速度大小相等,则根据v∝r分析。
例1 如图所示,rA=3rB=3rC,则:
(1)vA∶vB=________,
ωA∶ωB=________。
(2)ωA∶ωC=________,
vA∶vC=________。
例2 如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1∶3,则在传动的过程中( )
A.甲、乙两轮的角速度之比为1∶3
B.甲、乙两轮的周期之比为3∶1
C.甲、乙两轮边缘处的线速度大小之比为3∶1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1
例3 自行车用链条传动来驱动后轮前进,如图是链条传动的示意图,两个齿轮俗称“牙盘”。A、B、C分别为牙盘边缘和后轮边缘上的点,大齿轮半径为r1、小齿轮半径为r2、后轮半径为r3。下列说法正确的是( )
A.A、B两点的角速度相等
B.B、C两点的线速度大小相等
C.大、小齿轮的转速之比为
D.在水平路面匀速骑行时,脚踏板转一圈,自行车前进的距离为2πr3
二、圆周运动的周期性和多解问题
如图所示,直径为d的纸质圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略子弹重力、圆筒的阻力及空气阻力。问:
(1)子弹做什么运动?圆筒做什么运动?
(2)为什么圆筒上只有一个弹孔?
(3)子弹与圆筒的运动时间有何关系?
(4)子弹的速度v应满足什么条件?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等)。
(3)运动的关系:两物体运动的时间______。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间______。
(2)先特殊后一般:先考虑一个周期的情况,再根据运动的________,考虑多个周期时的规律。
(3)分析时注意两个运动是________,互不影响。
例4 如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L=2 m,当飞镖以初速度v0=10 m/s垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动,忽略空气阻力,重力加速度为g=10 m/s2,若飞镖恰好击中P点,求:
(1)圆盘的半径;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(2)圆盘转动周期的可能值。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
专题强化 圆周运动的传动问题和周期性问题
[学习目标]
1.熟练掌握描述圆周运动的各物理量之间的关系,掌握圆周运动中传动的特点(重点)。
2.会分析圆周运动中多解的原因,掌握解决圆周运动中的多解问题的方法(难点)。
一、圆周运动的传动问题
1.常见的传动装置及特点
项目 装置 特点 转动方向 规律
同轴转动 A、B两点在同轴的一个圆盘上 A、B两点角速度、周期相同 相同(填“相同”或“相反”) 线速度与半径成正比:=
皮带传动 两个轮子用皮带连接(皮带不打滑),A、B两点分别是两个轮子边缘上的点 A、B两点线速度大小相等 相同(填“相同”或“相反”) 角速度与半径成反比:= 周期与半径成正比:=
齿轮传动 两个齿轮轮齿吻合,A、B两点分别是两个齿轮边缘上的点,N1、N2分别为大齿轮和小齿轮的齿数 A、B两点线速度大小相等 相反(填“相同”或“相反”) 角速度与半径成反比,与齿轮齿数成反比:== 周期与半径成正比,与齿轮齿数成正比:==
摩擦传动 两摩擦轮靠摩擦进行传动(两轮不打滑),A点和B点分别是两轮边缘上的点 A、B两点线速度大小相等 相反(填“相同”或“相反”) 角速度与半径成反比:= 周期与半径成正比:=
2.求解传动问题的思路:
(1)分清传动特点:若属于皮带传动、齿轮传动或摩擦传动,则轮子边缘各点线速度大小相等;若属于同轴转动,则轮上各点的角速度相等。
(2)确定半径关系:根据装置中各点位置确定半径关系或根据题意确定半径关系。
(3)择式分析:若线速度大小相等,则根据ω∝分析;若角速度大小相等,则根据v∝r分析。
例1 如图所示,rA=3rB=3rC,则:
(1)vA∶vB= ,ωA∶ωB= 。
(2)ωA∶ωC= ,vA∶vC= 。
答案 (1)1∶1 1∶3 (2)1∶1 3∶1
例2 如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1∶3,则在传动的过程中( )
A.甲、乙两轮的角速度之比为1∶3
B.甲、乙两轮的周期之比为3∶1
C.甲、乙两轮边缘处的线速度大小之比为3∶1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1
答案 D
解析 齿轮传动中,两轮边缘的线速度大小相等,即线速度大小之比为1∶1,选项C错误;根据v=ωr,甲、乙两个轮子的半径之比为1∶3,故甲、乙两轮的角速度之比为ω1∶ω2=3∶1,选项A错误;周期T=,所以甲、乙两轮的周期之比T1∶T2=1∶3,选项B错误;根据线速度的定义v=可知,弧长Δs=vΔt,即甲、乙两轮边缘上的点相等时间内转过的弧长之比为1∶1,选项D正确。
例3 自行车用链条传动来驱动后轮前进,如图是链条传动的示意图,两个齿轮俗称“牙
盘”。A、B、C分别为牙盘边缘和后轮边缘上的点,大齿轮半径为r1、小齿轮半径为r2、后轮半径为r3。下列说法正确的是( )
A.A、B两点的角速度相等
B.B、C两点的线速度大小相等
C.大、小齿轮的转速之比为
D.在水平路面匀速骑行时,脚踏板转一圈,自行车前进的距离为2πr3
答案 D
解析 A、B两点属于皮带传动,线速度大小相等,因为半径不同,所以角速度不相等,故A错误;B、C两点属于同轴转动,角速度相等,因为半径不同,所以线速度大小不相等,故B错误;转速之比为===,故C错误;脚踏板转动一圈,自行车前进的距离为s=×2πr3=2πr3,故D正确。
二、圆周运动的周期性和多解问题
如图所示,直径为d的纸质圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略子弹重力、圆筒的阻力及空气阻力。问:
(1)子弹做什么运动?圆筒做什么运动?
(2)为什么圆筒上只有一个弹孔?
(3)子弹与圆筒的运动时间有何关系?
(4)子弹的速度v应满足什么条件?
答案 (1)子弹做匀速直线运动,圆筒做匀速圆周运动。
(2)子弹进圆筒时打了一个孔,恰好从这个孔出去,在子弹穿过圆筒过程中,圆筒转过了半圈或整数圈加半圈。
(3)子弹穿过圆筒的时间与圆筒转过半圈或整数圈加半圆的时间相等。
(4)子弹穿过圆筒所用时间t=,圆筒转过的角度θ=2nπ+π(n=0,1,2…),而ω=,联立可得v=(n=0,1,2…)。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等)。
(3)运动的关系:两物体运动的时间相等。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间相等。
(2)先特殊后一般:先考虑一个周期的情况,再根据运动的周期性,考虑多个周期时的规律。
(3)分析时注意两个运动是独立的,互不影响。
例4 如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L=2 m,当飞镖以初速度v0=10 m/s垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动,忽略空气阻力,重力加速度为g=10 m/s2,若飞镖恰好击中P点,求:
(1)圆盘的半径;
(2)圆盘转动周期的可能值。
答案 见解析
解析 (1)根据题意可知,飞镖做平抛运动,水平方向上有L=v0t,解得飞行时间为t==0.2 s,
竖直方向上有2R=gt2,
解得R=0.1 m=10 cm,
(2)根据题意,设圆盘转动的周期为T,则有t=T+kT(k=0,1,2,3…)
解得:T=(k=0,1,2,3…)。
