六年级下册数学课件-3.1 圆柱的体积 人教版(共92张PPT)
文档属性
| 名称 | 六年级下册数学课件-3.1 圆柱的体积 人教版(共92张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 20:48:49 | ||
图片预览




文档简介
(共92张PPT)
圆 柱 的 体 积
北师大版六年级数学下册
1.通过猜想与操作,推导出圆柱的体积公式,理解和掌握这一公式。
2.能够把圆柱的体积公式,应用于实际生活,计算圆柱形物体的体积和容器的容积。
3.培养同学们分析、推理的能力,渗透转化的数学思想。
4.通过猜想与应用,培养同学们的创新意识和实践能力。
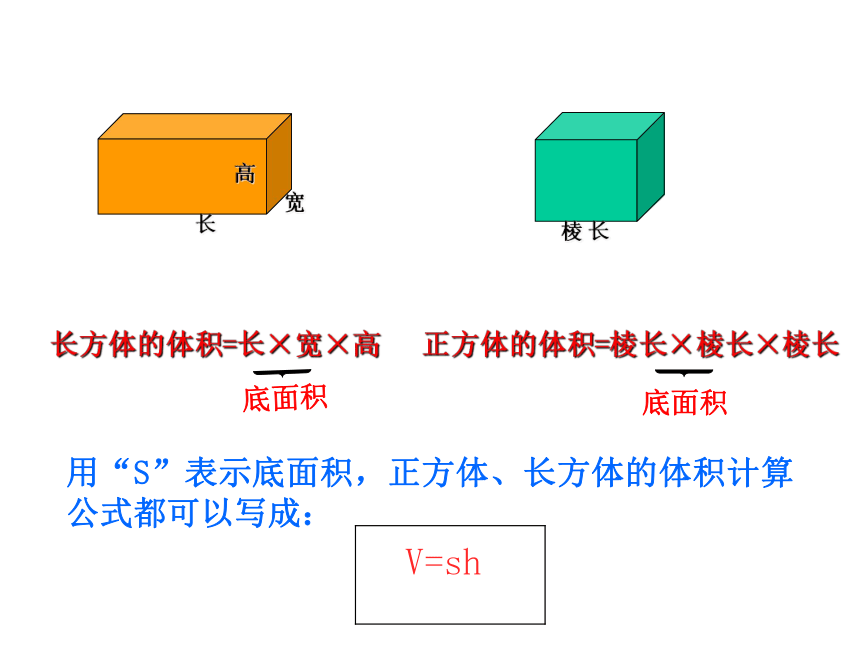
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长
宽
高
棱 长
底面积
底面积
V=sh
用“S”表示底面积,正方体、长方体的体积计算公式都可以写成:
导入铺垫
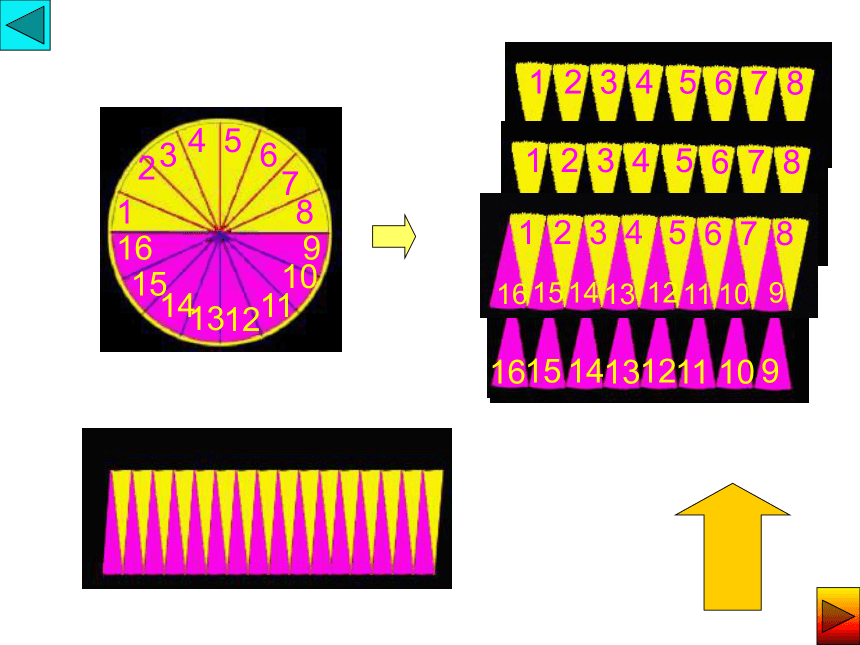
(1) 圆面积公式是怎样推导出来的?
(2)你学过哪些物体体积的计算公式?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
长
v
=a b h
v
3
正
=a
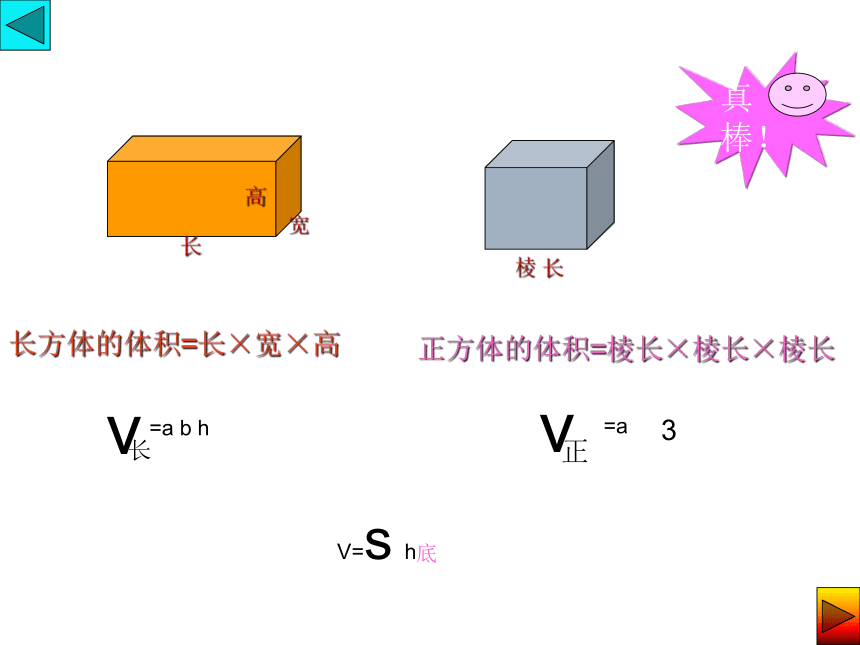
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
真 棒!
圆柱体积的大小与哪些条件有关?
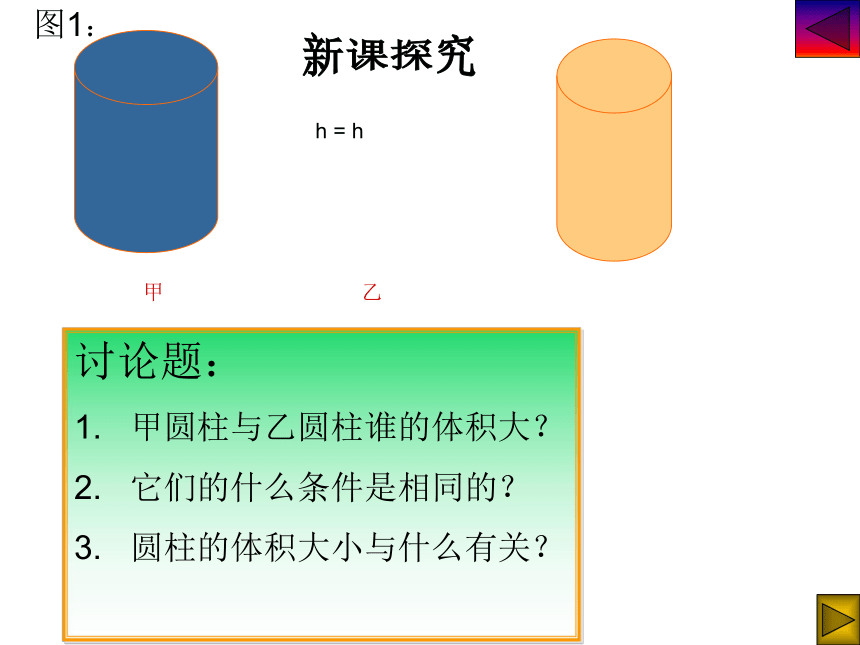
h = h
甲 乙
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
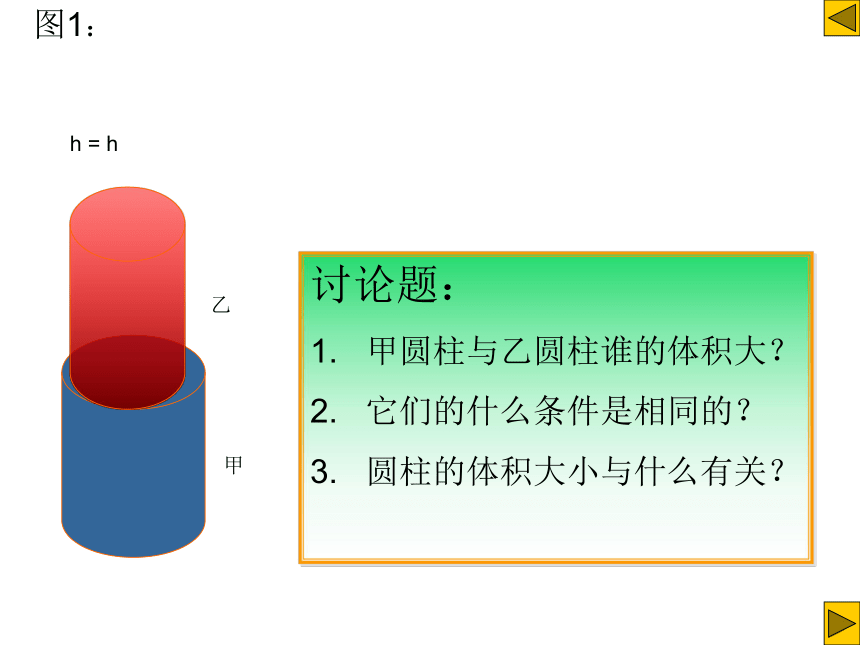
h = h
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
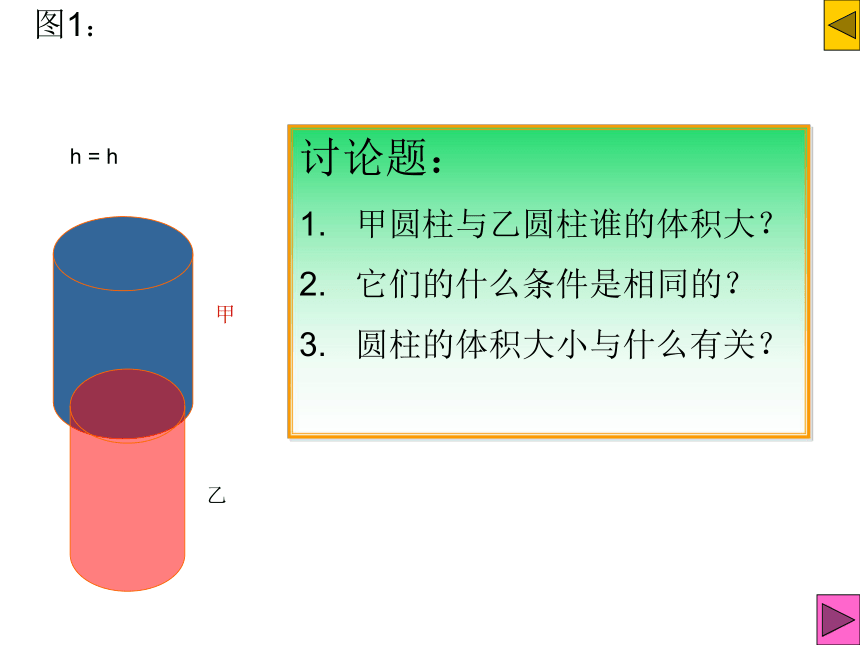
h = h
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
S = S
图
2
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
乙
S = S
乙
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
S = S
乙
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
S = S
圆柱体积的大小与哪些条件有关?
怎样求圆柱的体积呢?
底面积
高
长方体的体积=底面积 × 高
底面积
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 x 高
底面积
长方体的体积=底面积 x 高
高
长方体的体积=底面积 ×高
圆柱体的体积=
×
底面积
讨论
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
2.计算下列各圆柱的体积。
(1)底面直径8厘米,高是5厘米。
(2)底面半径是3分米,高是1.3米。
(3)底面周长是25.12分米,高是2分米。
例 1 一个圆柱形钢材,底面积是 20 平方
厘米,高是 1.5 米。它的体积是多少?
怎样解答
1.5 米 = 150 厘米
答: 它的体积是 3000 立方厘米。
圆柱的体积
20 × 150 = 3000 (立方厘米)
新 课
例2 一个圆柱形水桶,从里
面量底面直径是20厘米,
高是25厘米。这个水桶的
容积是多少立方分米?
例3、一根长2米的圆钢,横截面直径是6厘米,每立方厘米钢重7.8千克。这根圆金钢的重是多少千克?(得数保留整千克)
例4、一个圆柱形汽油桶,内底面半径2分米,高5分米,每升汽油重0.73千克。这个汽油桶能装汽油多少千克?(得数保留整千克)
例4
一根圆柱形钢材,底面积是50平方厘米,高是2.1米。它的体积是多少?
2.1米=210厘米
答:它的体积是10500立方厘米。
50×210=10500(立方厘米)
例5
一个圆柱形水桶,从里面量底面
直径是20厘米,高是25厘米。这
个水桶的容积是多少立方分米?
3.14×(-)×25
20
2
2
观察例4、例5有哪些相同点和不同点?
V=sh
V=兀(d÷2)×h
2
讨论
S h 求 V
r h 求 V
d h 求 V
C h 求 V
V=兀(C÷兀÷2) ×h
2
V= 兀r × h
2
先求S 再求V
先求r 再求S 然后求V
先求r 再求S 然后求V
做 一 做
答:它的体积是6750立方厘米。
75×90=6750(立方厘米)
(1)一根圆柱形木料,底面积为75平方厘米,长90厘米,它的体积是多少?
(2)一个圆柱行罐头盒的内底面半径是5厘米,高15厘米。它的容积是多少?
做 一 做
3.14×5 ×15
2
(1)
(2)
(3)
看图列式,并写出相应的公式。
V=s h
12×6
3.14 ×3 ×7
2
3.14 ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
6.28厘米
(4)
5厘米
练习巩固 应用拓展
把一根长1.5分米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
(9.6÷3)×1.5=4.8(立方分米)
答:这根钢材原来的体积是4.8立方分米。
(9.6÷4)×1.5=3.6(立方分米)
答:这根钢材原来的体积是3.6立方分米。
你能行!
1. 用绳子量出饮料罐底面的周长,然后通过周长求半径。用直尺量出高。
2. 用直尺量出直径(最长一条为直径),再通过直径求出半径。用直尺量出高。
怎样求出饮料罐的体积?
3. ?
V =s h
直柱体的体积 = 底面积×高
拓展
15平方米
8
米
9
米
20平方米
(1)你会计算它们的体积吗?
(2)试写出它们的体积公式。
想 一 想
试 一 试
3、判断正误,对的画“√”,错误 的画“×”。
(1)圆柱体的底面积越大,它的体积越大。
( )
(2)圆柱体的高越长,它的体积越大。
(3)圆柱体的体积与长方体的体积相等。
(4)圆柱体的底面直径和高可以相等。
( )
( )
( )
×
×
×
√
这节课你学会了什么?有什么感受?
完
填充。
⑴ 一个圆柱的底面积是 15 平方厘米,高是 6 厘米。它的体积是( )。
⑵ 一个圆柱的底面半径是 3 分米,高是 10 分米。它的体积是( )。
90 立方厘米
练一练2
圆柱的体积
282.6 立方分米
⑶ 一个圆柱的高是 5 分米,底面直径是 2 分米。它的体积是( )。
15.7 立方分米
⑷ 一个圆柱的体积是 180 立方分米,底面积是 30 平方分米。它的高是( )。
6 分米
圆 柱 的 体 积
北师大版六年级数学下册
1.通过猜想与操作,推导出圆柱的体积公式,理解和掌握这一公式。
2.能够把圆柱的体积公式,应用于实际生活,计算圆柱形物体的体积和容器的容积。
3.培养同学们分析、推理的能力,渗透转化的数学思想。
4.通过猜想与应用,培养同学们的创新意识和实践能力。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长
宽
高
棱 长
底面积
底面积
V=sh
用“S”表示底面积,正方体、长方体的体积计算公式都可以写成:
导入铺垫
(1) 圆面积公式是怎样推导出来的?
(2)你学过哪些物体体积的计算公式?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
1
2
3
4
5
6
7
8
16
9
10
12
13
14
15
11
长
v
=a b h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
真 棒!
圆柱体积的大小与哪些条件有关?
h = h
甲 乙
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
h = h
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
h = h
图1:
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
S = S
图
2
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
乙
S = S
乙
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
甲
乙
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
S = S
乙
甲
讨论题:
1. 甲圆柱与乙圆柱谁的体积大?
2. 它们的什么条件是相同的?
3. 圆柱的体积大小与什么有关?
S = S
圆柱体积的大小与哪些条件有关?
怎样求圆柱的体积呢?
底面积
高
长方体的体积=底面积 × 高
底面积
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 ×高
底面积
长方体的体积=底面积 x 高
底面积
长方体的体积=底面积 x 高
高
长方体的体积=底面积 ×高
圆柱体的体积=
×
底面积
讨论
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
2.计算下列各圆柱的体积。
(1)底面直径8厘米,高是5厘米。
(2)底面半径是3分米,高是1.3米。
(3)底面周长是25.12分米,高是2分米。
例 1 一个圆柱形钢材,底面积是 20 平方
厘米,高是 1.5 米。它的体积是多少?
怎样解答
1.5 米 = 150 厘米
答: 它的体积是 3000 立方厘米。
圆柱的体积
20 × 150 = 3000 (立方厘米)
新 课
例2 一个圆柱形水桶,从里
面量底面直径是20厘米,
高是25厘米。这个水桶的
容积是多少立方分米?
例3、一根长2米的圆钢,横截面直径是6厘米,每立方厘米钢重7.8千克。这根圆金钢的重是多少千克?(得数保留整千克)
例4、一个圆柱形汽油桶,内底面半径2分米,高5分米,每升汽油重0.73千克。这个汽油桶能装汽油多少千克?(得数保留整千克)
例4
一根圆柱形钢材,底面积是50平方厘米,高是2.1米。它的体积是多少?
2.1米=210厘米
答:它的体积是10500立方厘米。
50×210=10500(立方厘米)
例5
一个圆柱形水桶,从里面量底面
直径是20厘米,高是25厘米。这
个水桶的容积是多少立方分米?
3.14×(-)×25
20
2
2
观察例4、例5有哪些相同点和不同点?
V=sh
V=兀(d÷2)×h
2
讨论
S h 求 V
r h 求 V
d h 求 V
C h 求 V
V=兀(C÷兀÷2) ×h
2
V= 兀r × h
2
先求S 再求V
先求r 再求S 然后求V
先求r 再求S 然后求V
做 一 做
答:它的体积是6750立方厘米。
75×90=6750(立方厘米)
(1)一根圆柱形木料,底面积为75平方厘米,长90厘米,它的体积是多少?
(2)一个圆柱行罐头盒的内底面半径是5厘米,高15厘米。它的容积是多少?
做 一 做
3.14×5 ×15
2
(1)
(2)
(3)
看图列式,并写出相应的公式。
V=s h
12×6
3.14 ×3 ×7
2
3.14 ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
6.28厘米
(4)
5厘米
练习巩固 应用拓展
把一根长1.5分米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
(9.6÷3)×1.5=4.8(立方分米)
答:这根钢材原来的体积是4.8立方分米。
(9.6÷4)×1.5=3.6(立方分米)
答:这根钢材原来的体积是3.6立方分米。
你能行!
1. 用绳子量出饮料罐底面的周长,然后通过周长求半径。用直尺量出高。
2. 用直尺量出直径(最长一条为直径),再通过直径求出半径。用直尺量出高。
怎样求出饮料罐的体积?
3. ?
V =s h
直柱体的体积 = 底面积×高
拓展
15平方米
8
米
9
米
20平方米
(1)你会计算它们的体积吗?
(2)试写出它们的体积公式。
想 一 想
试 一 试
3、判断正误,对的画“√”,错误 的画“×”。
(1)圆柱体的底面积越大,它的体积越大。
( )
(2)圆柱体的高越长,它的体积越大。
(3)圆柱体的体积与长方体的体积相等。
(4)圆柱体的底面直径和高可以相等。
( )
( )
( )
×
×
×
√
这节课你学会了什么?有什么感受?
完
填充。
⑴ 一个圆柱的底面积是 15 平方厘米,高是 6 厘米。它的体积是( )。
⑵ 一个圆柱的底面半径是 3 分米,高是 10 分米。它的体积是( )。
90 立方厘米
练一练2
圆柱的体积
282.6 立方分米
⑶ 一个圆柱的高是 5 分米,底面直径是 2 分米。它的体积是( )。
15.7 立方分米
⑷ 一个圆柱的体积是 180 立方分米,底面积是 30 平方分米。它的高是( )。
6 分米
