5.1 比较简单的鸽巢原理 课件-人教版数学六年级下册(共21张PPT)
文档属性
| 名称 | 5.1 比较简单的鸽巢原理 课件-人教版数学六年级下册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第1课时 比较简单的鸽巢原理
第五单元 数学广角——鸽巢问题
游戏魔术
一副扑克牌拿走大小王之后,5个同学每人随意抽一张。
我猜至少有2个同学拿的是同花色的。
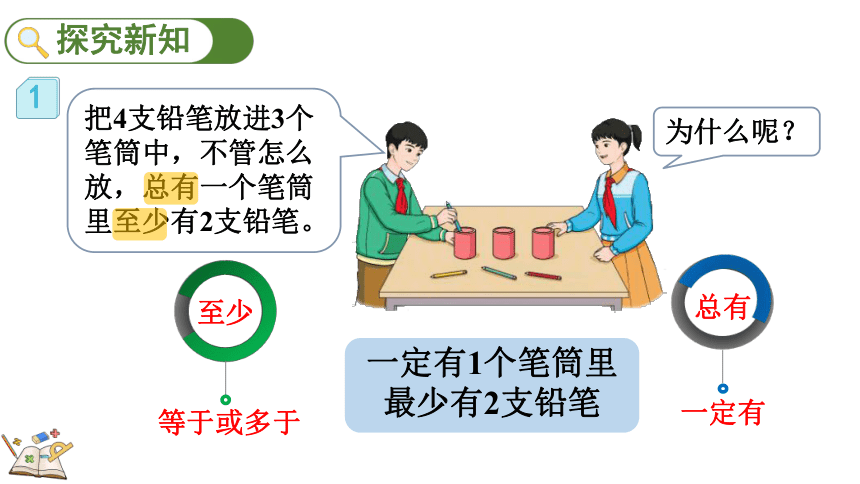
想一想:把4支铅笔放进3个笔筒中,你能怎么放呢?
1
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
为什么呢?
一定有
总有
等于或多于
至少
一定有1个笔筒里最少有2支铅笔
小组活动验证
1.借助实物或画图的方法(不考虑笔筒的顺序),自己动手摆一摆或画一画。
2.把每种情况记录下来,并思考怎样才能不重复、不遗漏。
3.观察并思考整个过程,说一说你发现了什么?(限时5分钟)
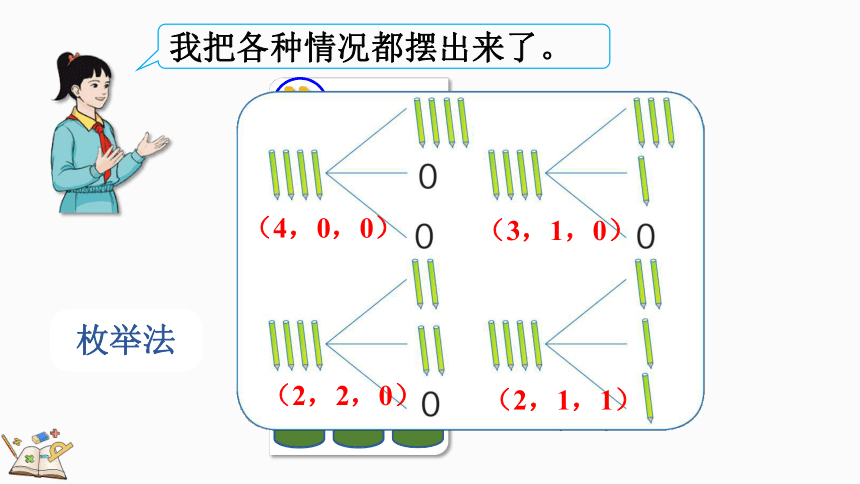
(4,0,0)
(2,1,1)
(3,1,0)
(2,2,0)
我把各种情况都摆出来了。
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
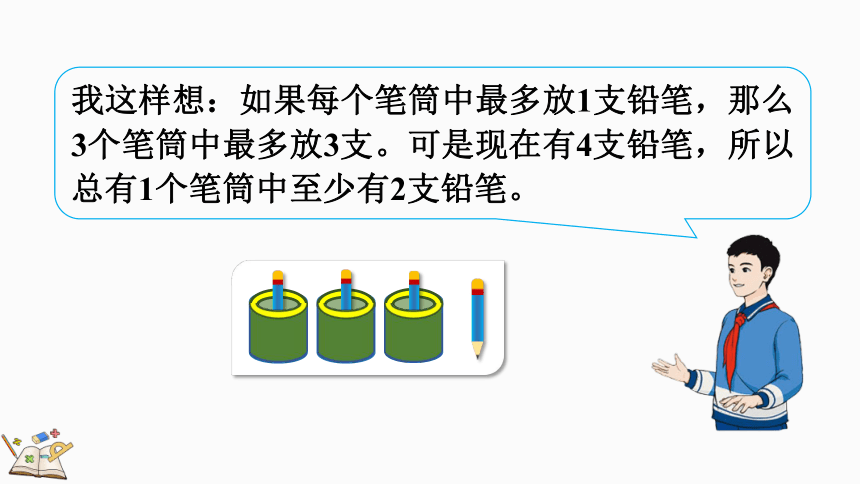
我这样想:如果每个笔筒中最多放1支铅笔,那么3个笔筒中最多放3支。可是现在有4支铅笔,所以总有1个笔筒中至少有2支铅笔。
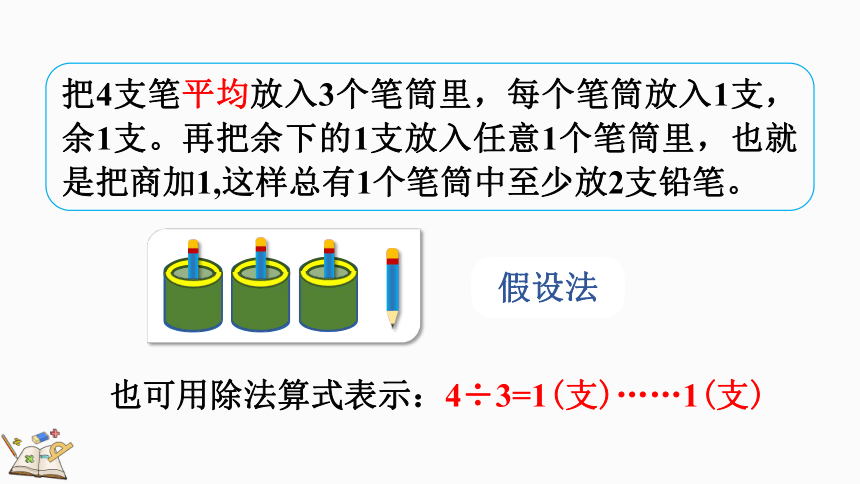
把4支笔平均放入3个笔筒里,每个笔筒放入1支,余1支。再把余下的1支放入任意1个笔筒里,也就是把商加1,这样总有1个笔筒中至少放2支铅笔。
也可用除法算式表示:4÷3=1(支)……1(支)
假设法
5支铅笔放入4个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
6支铅笔放入5个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
10支铅笔放入9个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
100支铅笔放入99个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
只要铅笔比笔筒的数量多( ),总有1个笔筒里至少放( )支铅笔。
2
1
说一说
(n+1)只鸽子飞进n个鸽巢里(n为非0自然数),总有1个鸽巢里至少飞进2只鸽子。
鸽巢原理
铅笔……鸽子
笔筒……鸽巢
随意找13位老师,他们中至少有2个人的属相相同。为什么?
选自教材第67页做一做第1题
1
如果12位老师的属相都不相同,还剩下1位老师的属相一定和其中某位老师的属相相同,所以随意找13位老师,他们中至少有2个人的属相相同。
12个鸽巢
13只鸽子
选自教材第67页做一做第2题
2
5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
2
5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
鸽巢
鸽子的个数大于鸽巢的个数,不论怎么飞,总有1个鸽巢至少飞进两只鸽子。
1.扑克牌中一共有4种花色,假设前4个人拿的牌花色不一样,那么第5个人拿的牌花色一定和前4人中的一人重复。
红桃
①
梅花
②
方片
③
黑桃
④
一副牌,取出大小王,还剩52张牌,5人每人随意抽一张,至少有2张牌是同花色的,是成立的。
⑤
拿的牌要么是红桃,要么是梅花、方片、黑桃。
你理解前面扑克牌魔术的道理了吗?
2
2.填一填。
3只鸽子
2个鸽巢
“3只鸽子”飞进“2个鸽巢”中,必然有1个“鸽巢”至少飞进2只“鸽子”,即至少有2个小朋友性别相同。
3个小朋友同行,其中必有( )个小朋友性别相同。
抢凳子游戏:6个人抢4张凳子。
音乐停止时,会出现什么情况?为什么?
点击右图播放音乐
那么剩下的2个人坐的凳子一定和前4人中有重复。一定有1张
凳子上至少坐2人。
假设前4人坐的凳子不一样,
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有1个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有1个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
这节课有什么收获呢?
鸽巢问题
1.先要分清鸽巢和所分的物体,再看清它
们的个数。
2.巧妙建造鸽巢,使鸽巢比要分的物体少。
1.从教材课后习题中选取;
2.从课时练中选取。
鸽巢问题
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
4÷3=1(支)……1(支)
假设法
第1课时 比较简单的鸽巢原理
第五单元 数学广角——鸽巢问题
游戏魔术
一副扑克牌拿走大小王之后,5个同学每人随意抽一张。
我猜至少有2个同学拿的是同花色的。
想一想:把4支铅笔放进3个笔筒中,你能怎么放呢?
1
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
为什么呢?
一定有
总有
等于或多于
至少
一定有1个笔筒里最少有2支铅笔
小组活动验证
1.借助实物或画图的方法(不考虑笔筒的顺序),自己动手摆一摆或画一画。
2.把每种情况记录下来,并思考怎样才能不重复、不遗漏。
3.观察并思考整个过程,说一说你发现了什么?(限时5分钟)
(4,0,0)
(2,1,1)
(3,1,0)
(2,2,0)
我把各种情况都摆出来了。
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
我这样想:如果每个笔筒中最多放1支铅笔,那么3个笔筒中最多放3支。可是现在有4支铅笔,所以总有1个笔筒中至少有2支铅笔。
把4支笔平均放入3个笔筒里,每个笔筒放入1支,余1支。再把余下的1支放入任意1个笔筒里,也就是把商加1,这样总有1个笔筒中至少放2支铅笔。
也可用除法算式表示:4÷3=1(支)……1(支)
假设法
5支铅笔放入4个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
6支铅笔放入5个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
10支铅笔放入9个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
100支铅笔放入99个笔筒里,总有1个笔筒里至少放( )支铅笔。
2
只要铅笔比笔筒的数量多( ),总有1个笔筒里至少放( )支铅笔。
2
1
说一说
(n+1)只鸽子飞进n个鸽巢里(n为非0自然数),总有1个鸽巢里至少飞进2只鸽子。
鸽巢原理
铅笔……鸽子
笔筒……鸽巢
随意找13位老师,他们中至少有2个人的属相相同。为什么?
选自教材第67页做一做第1题
1
如果12位老师的属相都不相同,还剩下1位老师的属相一定和其中某位老师的属相相同,所以随意找13位老师,他们中至少有2个人的属相相同。
12个鸽巢
13只鸽子
选自教材第67页做一做第2题
2
5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
2
5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
鸽巢
鸽子的个数大于鸽巢的个数,不论怎么飞,总有1个鸽巢至少飞进两只鸽子。
1.扑克牌中一共有4种花色,假设前4个人拿的牌花色不一样,那么第5个人拿的牌花色一定和前4人中的一人重复。
红桃
①
梅花
②
方片
③
黑桃
④
一副牌,取出大小王,还剩52张牌,5人每人随意抽一张,至少有2张牌是同花色的,是成立的。
⑤
拿的牌要么是红桃,要么是梅花、方片、黑桃。
你理解前面扑克牌魔术的道理了吗?
2
2.填一填。
3只鸽子
2个鸽巢
“3只鸽子”飞进“2个鸽巢”中,必然有1个“鸽巢”至少飞进2只“鸽子”,即至少有2个小朋友性别相同。
3个小朋友同行,其中必有( )个小朋友性别相同。
抢凳子游戏:6个人抢4张凳子。
音乐停止时,会出现什么情况?为什么?
点击右图播放音乐
那么剩下的2个人坐的凳子一定和前4人中有重复。一定有1张
凳子上至少坐2人。
假设前4人坐的凳子不一样,
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有1个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有1个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
这节课有什么收获呢?
鸽巢问题
1.先要分清鸽巢和所分的物体,再看清它
们的个数。
2.巧妙建造鸽巢,使鸽巢比要分的物体少。
1.从教材课后习题中选取;
2.从课时练中选取。
鸽巢问题
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
4÷3=1(支)……1(支)
假设法
