5.1导数的概念及其意义 同步练习(含解析)
文档属性
| 名称 | 5.1导数的概念及其意义 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 23:10:21 | ||
图片预览




文档简介
5.1导数的概念及其意义同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数的图象在点处的切线方程是( )
A. B. C. D.
2.若,则( )
A. B.4 C.2 D.
3.已知函数在上可导,且满足,则函数在点处的切线的方程为( )
A. B. C. D.
4.物体甲、乙在时间到范围内,路程的变化情况如图所示,下列说法正确的是( )
A.在到范围内,甲的平均速度大于乙的平均速度
B.在到范围内,甲的平均速度小于乙的平均速度
C.在到范围内,甲的平均速度大于乙的平均速度
D.在到范围内,甲的平均速度小于乙的平均速度
5.设P为曲线C:上的点,且曲线C在点P处切线倾斜角的取值范围是,则点P横坐标的取值范围为( )
A. B.
C. D.
6.已知函数在处可导,若,则( )
A.1 B. C.2 D.8
7.为了响应国家节能减排的号召,甲 乙两个工厂进行了污水排放治理,已知某月两厂污水的排放量与时间的关系如图所示,下列说法正确的是( )
A.该月内,甲乙两厂中甲厂污水排放量减少得更多
B.该月内,甲厂污水排放量减少的速度是先慢后快
C.在接近时,甲乙两厂中乙厂污水排放量减少得更快
D.该月内存在某一时刻,甲 乙两厂污水排放量减少的速度相同
8.已知函数的导函数为,的图象如图所示,则( )
A. B.
C. D.
二、多选题
9.各地房产部门为尽快稳定房价,提出多种房产供应方案,其中之一就是在规定的时间T内完成房产供应量任务.已知房产供应量Q与时间t的函数关系如图所示,则在以下四种房产供应方案中,在时间内供应效率(单位时间的供应量)不逐步提高的有( )
A. B. C. D.
10.已知,在R上连续且可导,且,下列关于导数与极限的说法中正确的是( )
A. B.
C. D.
11.已知函数,则( )
A.在定义域上单调递增 B.曲线上任意一点处的切线斜率大于0
C.的图象关于点对称 D.
12.若的图象在处的切线分别为,且,则( )
A.
B.的最小值为2
C.在轴上的截距之差为2
D.在轴上的截距之积可能为
三、填空题
13.已知直线与曲线相切,切点为,与曲线也相切,切点是,则的值为 .
14.已知曲线,则曲线过点的切线方程为 .
15.某物体做匀速直线运动,其方程为,则该物体在运动过程中其平均速度与任意时刻的瞬时速度的关系是 .
16.牛顿迭代法又称牛顿—拉夫逊方法,它是牛顿在17世纪提出的一种在实数集上近似求解方程根的一种方法,具体步骤如下:设是函数的一个零点,任意选取作为的初始近似值,过点作曲线的切线,设与轴交点的横坐标为,并称为的1次近似值;过点作曲线的切线,设与轴交点的横坐标为,称为的2次近似值,过点作曲线的切线,记与轴交点的横坐标为,并称为的次近似值,设的零点为,取,则的2次近似值为 ;设,数列的前项积为.若任意的恒成立,则整数的最小值为 .
四、解答题
17.已知函数,且.
(1)求的值;
(2)设,求过点的切线方程.
18.如果一个质点由定点A开始运动,其位移y关于时间t的函数为.
(1)当,时,求和;
(2)求函数在处的导数.
19.路灯距地面,一个身高为的人以84 m/min的速度在地面上从路灯在地面上的射影C点处沿直线匀速离开路灯.
(1)求身影的长度y(单位:m)与人距C点的距离x(单位:m)之间的关系式;
(2)求人离开C点10 s内身影长度的平均变化率.
20.在直角坐标系中,抛物线与直线交于两点.
(1)若点的横坐标为4,求抛物线在点处的切线方程;
(2)探究轴上是否存在点,使得当变动时,总有?若存在,求出点坐标;若不存在,请说明理由.
21.巍巍泰山为我国的五岳之首,有“天下第一山”之美誉,登泰山在当地有用“紧十八,慢十八,不紧不慢又十八”的俗语来形容爬十八盘的感受,下面是一段登山路线图.同样是登山,从处到处会感觉比较轻松,而从处到处会感觉比较吃力.试用数学语言给出解释.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】利用导数的几何意义求切线方程.
【详解】因为,所以,所以切点为,又,
由导数的几何意义知函数的图象在点处的切线斜率,
故得函数的图象在点处的切线方程是,即为.
故选:B
2.B
【分析】根据导数的定义,分母是自变量的改变量即,所以把所求的式子分母变为即可求解.
【详解】
故选:B
3.D
【分析】根据条件,利用导数的定义即可得到,再由导数的几何意义即可得出结果.
【详解】由,得到,
由导数的定义知,所以函数在点处的切线的方程为,
即,
故选:D.
4.C
【分析】利用平均速度的定义逐项判断可得出合适的选项.
【详解】在到范围内,甲、乙的平均速度都为,故AB错误;
在到范围内,甲的平均速度为,乙的平均速度为,
因为,,所以,
则在到范围内,甲的平均速度大于乙的平均速度,故C正确,D错误.
故选:C.
5.D
【分析】先根据导数的概念求出函数的导数,然后根据导数的几何意义结合点P处切线倾斜角的取值范围是,列不等式可求出结果.
【详解】
又曲线C在点P处切线倾斜角的取值范围为,
所以其斜率,
所以,解得,
所以点P横坐标的取值范围为,
故选:D.
6.A
【分析】利用计算即可.
【详解】
.
故选:A.
7.D
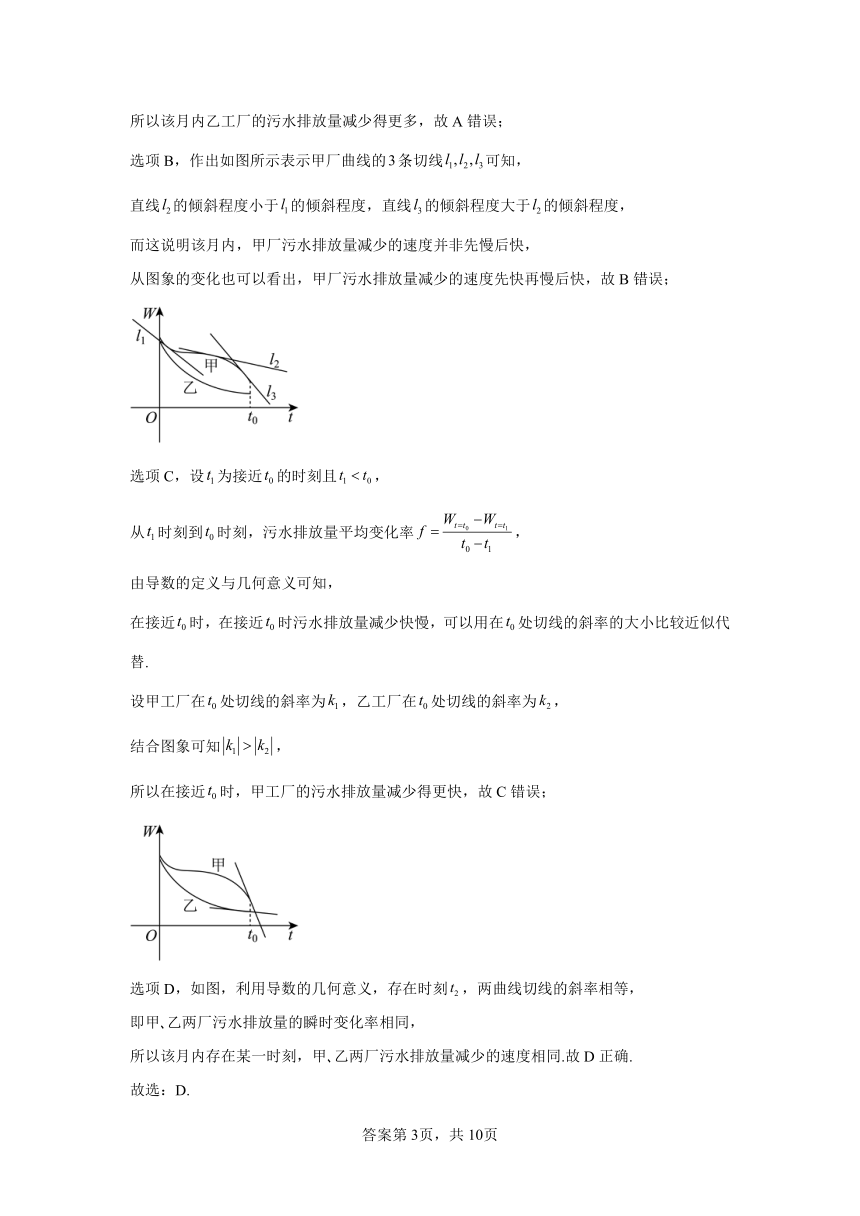
【分析】选项A,结合图象,比较两厂污水排放量减少量即可求解;选项B,由切线倾斜程度的大小比较可得;选项C,在接近时污水排放量减少快慢,可以用在处切线的斜率的大小比较近似代替,比较两曲线在处切线的斜率的绝对值大小即可得;选项D,利用导数的几何意义,存在某一时刻,甲 乙两厂污水排放量的瞬时变化率即切线的斜率相等,则甲 乙两厂污水排放量减少的速度相同.
【详解】选项A,设,
设甲工厂的污水排放量减少为,乙工厂的污水排放量减少为,
结合图像可知:,
所以该月内乙工厂的污水排放量减少得更多,故A错误;
选项B,作出如图所示表示甲厂曲线的条切线可知,
直线的倾斜程度小于的倾斜程度,直线的倾斜程度大于的倾斜程度,
而这说明该月内,甲厂污水排放量减少的速度并非先慢后快,
从图象的变化也可以看出,甲厂污水排放量减少的速度先快再慢后快,故B错误;
选项C,设为接近的时刻且,
从时刻到时刻,污水排放量平均变化率,
由导数的定义与几何意义可知,
在接近时,在接近时污水排放量减少快慢,可以用在处切线的斜率的大小比较近似代替.
设甲工厂在处切线的斜率为,乙工厂在处切线的斜率为,
结合图象可知,
所以在接近时,甲工厂的污水排放量减少得更快,故C错误;
选项D,如图,利用导数的几何意义,存在时刻,两曲线切线的斜率相等,
即甲 乙两厂污水排放量的瞬时变化率相同,
所以该月内存在某一时刻,甲 乙两厂污水排放量减少的速度相同.故D正确.
故选:D.
8.B
【分析】根据已知条件作出切线,利用导数的几何意义及斜率的定义即可得.
【详解】依次作出函数在处的切线,如图所示:
根据导数的几何意义及图形中切线的斜率可知,
.
故选:B.
9.ACD
【分析】根据变化率的知识,结合曲线在某点处的导数的几何意义可得结果.
【详解】当单位时间的供应量逐步提高时,供应量的增长速度越来越快,图象上切线的斜率随着自变量的增加会越来越大,
故曲线是上升的,且越来越陡峭,
所以函数的图象应一直是下凹的,则选项B满足条件,
所以在时间内供应效率(单位时间的供应量)不逐步提高的有ACD选项.
故选:ACD.
10.BCD
【分析】利用导数的定义逐个求解.
【详解】,故A错;
,故B对;
,由导数的定义知C对;
,故D对;
故选:BCD
11.BD
【分析】由指数型复合函数单调性即可判断A;求导即可判断B;由题可知,由此即可判断C;由C选项结论即可判断D.
【详解】对A,,,
根据复合函数单调性知在,上单调递增,
当时,,当时,,∴在定义域上不是单调递增,故A错误;
对B,因为,故B正确;
对C,∵,∴,
∴的图象关于点对称,故C错误;
∵,由可得D正确.
故选:BD.
12.AC
【分析】根据及导数的几何意义得,再借助基本不等式即可判断A,B;写出的方程,得到在轴上的截距分别为,由此判断C,D.
【详解】对于A,B:由题意可得,当时,,当时,,
所以的斜率分别为,
因为,所以,得,
因为,所以,
故A正确,B错误.
对于C,D:的方程为,即,
令,得,所以在轴上的截距为,
的方程为,可得在轴上的截距为,
所以在轴上的截距之差为,
在轴上的截距之积为,故C正确,D错误.
故选:AC
13.1
【分析】根据导数求出切线的斜率,得到切线方程,根据两切线相同列出等式即可得解.
【详解】设直线与曲线相切于,又,所以直线的斜率为,
则处的切线方程为,即;
直线与曲线相切于,,
可得切线方程为,
即,
因为直线与两条曲线都相切,所以两条切线相同,
则且,
则,即
可得,解得,
故答案为:.
14.或
【分析】由题意首先根据定义得导函数,进一步求出切点即可得解.
【详解】点不在曲线上.
设所求切线的切点为,
则切线的斜率,
故所求的切线方程为,
将及代入上式,得,
解得或,所以切点为或.
从而所求切线方程为或.
故答案为:或.
15.相等
【分析】先得出平均速度的表达式,发现它刚好等于瞬时速度,由此即可得解.
【详解】设平均速度为,瞬时速度为v.
所以,
故平均速度与任意时刻的瞬时速度相等.
故答案为:相等.
16.
【分析】利用导数求出直线的方程,可得出,结合可求出的值,推导出,可求得,进而可求得整数的最小值.
【详解】,则,,
所以,曲线在点处的切线方程为,即,
由题意可知点在直线上,
所以,,,则,,
,,
因为函数的零点近似值为r,且函数在上为增函数,
因为,,由零点存在定理可知,
由题意可知,,故整数的最小值为2.
故答案为:;2
【点睛】关键点点睛:本题考查数列不等式恒成立问题,解题的关键在于利用导数求出切线方程,得出数列的递推公式,利用数列的递推公式求解.
17.(1)
(2)
【分析】(1)利用导数求解参数即可.
(2)先设切点,利用导数表示斜率,建立方程求出参数,再写切线方程即可.
【详解】(1)定义域为,,
而,而已知,可得,
解得,故的值为,
(2),设切点为,设切线斜率为,
而,故切线方程为,
将代入方程中,可得,解得(负根舍去),
故切线方程为,
18.(1),
(2)48
【分析】(1)由平均变化率公式计算即可;
(2)由导数的定义计算即可.
【详解】(1),
故当,时,,.
(2)由(1)得,
故函数在处的导数是48.
19.(1);
(2)0.35 m/s.
【分析】(1)根据题设,利用相似比,列方程即可得关系式;
(2)根据(1)所得关系,分别求出区间内对应自变量、函数值的增量,即可得平均变化率.
【详解】(1)如题图,设人从C点运动到B点位移为x m,AB为身影长度,为y m,
由于,则,即,所以.
(2)设人离开C点的时间为t s,而,而,所以.
在内自变量的增量为,
函数值的增量为,
所以.
即人离开C点10 s内身影长度的平均变化率为 m/s.
20.(1)
(2)存在;
【分析】(1)根据导数的几何意义求解;
(2)总有,即直线与直线的倾斜角互补,即恒有,联立直线与抛物线方程,得到韦达定理代入运算,判断得解.
【详解】(1)由已知,得,因为,所以,斜率,
因此,切线方程为,即.
(2)存在符合题意的点,理由如下:
设点为符合题意的点,,直线的斜率分别为.
联立方程,得,
因为,则,可得,
从而
,
因为不恒为0,可知当且仅当时,恒有,
则直线与直线的倾斜角互补,故,
所以点符合题意.
21.答案见解析
【分析】计算从处到处高度的平均变化率,从处到处高度的平均变化率,再比较两值的大小说明吃力的原因.
【详解】山路从A处到B处高度的平均变化率为,
山路从C处到D处高度的平均变化率为,
由知,山路从C处到D处比从A处到B处陡峭.
故从A处到B处会感觉比较轻松,而从C处到D处会感觉比较吃力.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数的图象在点处的切线方程是( )
A. B. C. D.
2.若,则( )
A. B.4 C.2 D.
3.已知函数在上可导,且满足,则函数在点处的切线的方程为( )
A. B. C. D.
4.物体甲、乙在时间到范围内,路程的变化情况如图所示,下列说法正确的是( )
A.在到范围内,甲的平均速度大于乙的平均速度
B.在到范围内,甲的平均速度小于乙的平均速度
C.在到范围内,甲的平均速度大于乙的平均速度
D.在到范围内,甲的平均速度小于乙的平均速度
5.设P为曲线C:上的点,且曲线C在点P处切线倾斜角的取值范围是,则点P横坐标的取值范围为( )
A. B.
C. D.
6.已知函数在处可导,若,则( )
A.1 B. C.2 D.8
7.为了响应国家节能减排的号召,甲 乙两个工厂进行了污水排放治理,已知某月两厂污水的排放量与时间的关系如图所示,下列说法正确的是( )
A.该月内,甲乙两厂中甲厂污水排放量减少得更多
B.该月内,甲厂污水排放量减少的速度是先慢后快
C.在接近时,甲乙两厂中乙厂污水排放量减少得更快
D.该月内存在某一时刻,甲 乙两厂污水排放量减少的速度相同
8.已知函数的导函数为,的图象如图所示,则( )
A. B.
C. D.
二、多选题
9.各地房产部门为尽快稳定房价,提出多种房产供应方案,其中之一就是在规定的时间T内完成房产供应量任务.已知房产供应量Q与时间t的函数关系如图所示,则在以下四种房产供应方案中,在时间内供应效率(单位时间的供应量)不逐步提高的有( )
A. B. C. D.
10.已知,在R上连续且可导,且,下列关于导数与极限的说法中正确的是( )
A. B.
C. D.
11.已知函数,则( )
A.在定义域上单调递增 B.曲线上任意一点处的切线斜率大于0
C.的图象关于点对称 D.
12.若的图象在处的切线分别为,且,则( )
A.
B.的最小值为2
C.在轴上的截距之差为2
D.在轴上的截距之积可能为
三、填空题
13.已知直线与曲线相切,切点为,与曲线也相切,切点是,则的值为 .
14.已知曲线,则曲线过点的切线方程为 .
15.某物体做匀速直线运动,其方程为,则该物体在运动过程中其平均速度与任意时刻的瞬时速度的关系是 .
16.牛顿迭代法又称牛顿—拉夫逊方法,它是牛顿在17世纪提出的一种在实数集上近似求解方程根的一种方法,具体步骤如下:设是函数的一个零点,任意选取作为的初始近似值,过点作曲线的切线,设与轴交点的横坐标为,并称为的1次近似值;过点作曲线的切线,设与轴交点的横坐标为,称为的2次近似值,过点作曲线的切线,记与轴交点的横坐标为,并称为的次近似值,设的零点为,取,则的2次近似值为 ;设,数列的前项积为.若任意的恒成立,则整数的最小值为 .
四、解答题
17.已知函数,且.
(1)求的值;
(2)设,求过点的切线方程.
18.如果一个质点由定点A开始运动,其位移y关于时间t的函数为.
(1)当,时,求和;
(2)求函数在处的导数.
19.路灯距地面,一个身高为的人以84 m/min的速度在地面上从路灯在地面上的射影C点处沿直线匀速离开路灯.
(1)求身影的长度y(单位:m)与人距C点的距离x(单位:m)之间的关系式;
(2)求人离开C点10 s内身影长度的平均变化率.
20.在直角坐标系中,抛物线与直线交于两点.
(1)若点的横坐标为4,求抛物线在点处的切线方程;
(2)探究轴上是否存在点,使得当变动时,总有?若存在,求出点坐标;若不存在,请说明理由.
21.巍巍泰山为我国的五岳之首,有“天下第一山”之美誉,登泰山在当地有用“紧十八,慢十八,不紧不慢又十八”的俗语来形容爬十八盘的感受,下面是一段登山路线图.同样是登山,从处到处会感觉比较轻松,而从处到处会感觉比较吃力.试用数学语言给出解释.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】利用导数的几何意义求切线方程.
【详解】因为,所以,所以切点为,又,
由导数的几何意义知函数的图象在点处的切线斜率,
故得函数的图象在点处的切线方程是,即为.
故选:B
2.B
【分析】根据导数的定义,分母是自变量的改变量即,所以把所求的式子分母变为即可求解.
【详解】
故选:B
3.D
【分析】根据条件,利用导数的定义即可得到,再由导数的几何意义即可得出结果.
【详解】由,得到,
由导数的定义知,所以函数在点处的切线的方程为,
即,
故选:D.
4.C
【分析】利用平均速度的定义逐项判断可得出合适的选项.
【详解】在到范围内,甲、乙的平均速度都为,故AB错误;
在到范围内,甲的平均速度为,乙的平均速度为,
因为,,所以,
则在到范围内,甲的平均速度大于乙的平均速度,故C正确,D错误.
故选:C.
5.D
【分析】先根据导数的概念求出函数的导数,然后根据导数的几何意义结合点P处切线倾斜角的取值范围是,列不等式可求出结果.
【详解】
又曲线C在点P处切线倾斜角的取值范围为,
所以其斜率,
所以,解得,
所以点P横坐标的取值范围为,
故选:D.
6.A
【分析】利用计算即可.
【详解】
.
故选:A.
7.D
【分析】选项A,结合图象,比较两厂污水排放量减少量即可求解;选项B,由切线倾斜程度的大小比较可得;选项C,在接近时污水排放量减少快慢,可以用在处切线的斜率的大小比较近似代替,比较两曲线在处切线的斜率的绝对值大小即可得;选项D,利用导数的几何意义,存在某一时刻,甲 乙两厂污水排放量的瞬时变化率即切线的斜率相等,则甲 乙两厂污水排放量减少的速度相同.
【详解】选项A,设,
设甲工厂的污水排放量减少为,乙工厂的污水排放量减少为,
结合图像可知:,
所以该月内乙工厂的污水排放量减少得更多,故A错误;
选项B,作出如图所示表示甲厂曲线的条切线可知,
直线的倾斜程度小于的倾斜程度,直线的倾斜程度大于的倾斜程度,
而这说明该月内,甲厂污水排放量减少的速度并非先慢后快,
从图象的变化也可以看出,甲厂污水排放量减少的速度先快再慢后快,故B错误;
选项C,设为接近的时刻且,
从时刻到时刻,污水排放量平均变化率,
由导数的定义与几何意义可知,
在接近时,在接近时污水排放量减少快慢,可以用在处切线的斜率的大小比较近似代替.
设甲工厂在处切线的斜率为,乙工厂在处切线的斜率为,
结合图象可知,
所以在接近时,甲工厂的污水排放量减少得更快,故C错误;
选项D,如图,利用导数的几何意义,存在时刻,两曲线切线的斜率相等,
即甲 乙两厂污水排放量的瞬时变化率相同,
所以该月内存在某一时刻,甲 乙两厂污水排放量减少的速度相同.故D正确.
故选:D.
8.B
【分析】根据已知条件作出切线,利用导数的几何意义及斜率的定义即可得.
【详解】依次作出函数在处的切线,如图所示:
根据导数的几何意义及图形中切线的斜率可知,
.
故选:B.
9.ACD
【分析】根据变化率的知识,结合曲线在某点处的导数的几何意义可得结果.
【详解】当单位时间的供应量逐步提高时,供应量的增长速度越来越快,图象上切线的斜率随着自变量的增加会越来越大,
故曲线是上升的,且越来越陡峭,
所以函数的图象应一直是下凹的,则选项B满足条件,
所以在时间内供应效率(单位时间的供应量)不逐步提高的有ACD选项.
故选:ACD.
10.BCD
【分析】利用导数的定义逐个求解.
【详解】,故A错;
,故B对;
,由导数的定义知C对;
,故D对;
故选:BCD
11.BD
【分析】由指数型复合函数单调性即可判断A;求导即可判断B;由题可知,由此即可判断C;由C选项结论即可判断D.
【详解】对A,,,
根据复合函数单调性知在,上单调递增,
当时,,当时,,∴在定义域上不是单调递增,故A错误;
对B,因为,故B正确;
对C,∵,∴,
∴的图象关于点对称,故C错误;
∵,由可得D正确.
故选:BD.
12.AC
【分析】根据及导数的几何意义得,再借助基本不等式即可判断A,B;写出的方程,得到在轴上的截距分别为,由此判断C,D.
【详解】对于A,B:由题意可得,当时,,当时,,
所以的斜率分别为,
因为,所以,得,
因为,所以,
故A正确,B错误.
对于C,D:的方程为,即,
令,得,所以在轴上的截距为,
的方程为,可得在轴上的截距为,
所以在轴上的截距之差为,
在轴上的截距之积为,故C正确,D错误.
故选:AC
13.1
【分析】根据导数求出切线的斜率,得到切线方程,根据两切线相同列出等式即可得解.
【详解】设直线与曲线相切于,又,所以直线的斜率为,
则处的切线方程为,即;
直线与曲线相切于,,
可得切线方程为,
即,
因为直线与两条曲线都相切,所以两条切线相同,
则且,
则,即
可得,解得,
故答案为:.
14.或
【分析】由题意首先根据定义得导函数,进一步求出切点即可得解.
【详解】点不在曲线上.
设所求切线的切点为,
则切线的斜率,
故所求的切线方程为,
将及代入上式,得,
解得或,所以切点为或.
从而所求切线方程为或.
故答案为:或.
15.相等
【分析】先得出平均速度的表达式,发现它刚好等于瞬时速度,由此即可得解.
【详解】设平均速度为,瞬时速度为v.
所以,
故平均速度与任意时刻的瞬时速度相等.
故答案为:相等.
16.
【分析】利用导数求出直线的方程,可得出,结合可求出的值,推导出,可求得,进而可求得整数的最小值.
【详解】,则,,
所以,曲线在点处的切线方程为,即,
由题意可知点在直线上,
所以,,,则,,
,,
因为函数的零点近似值为r,且函数在上为增函数,
因为,,由零点存在定理可知,
由题意可知,,故整数的最小值为2.
故答案为:;2
【点睛】关键点点睛:本题考查数列不等式恒成立问题,解题的关键在于利用导数求出切线方程,得出数列的递推公式,利用数列的递推公式求解.
17.(1)
(2)
【分析】(1)利用导数求解参数即可.
(2)先设切点,利用导数表示斜率,建立方程求出参数,再写切线方程即可.
【详解】(1)定义域为,,
而,而已知,可得,
解得,故的值为,
(2),设切点为,设切线斜率为,
而,故切线方程为,
将代入方程中,可得,解得(负根舍去),
故切线方程为,
18.(1),
(2)48
【分析】(1)由平均变化率公式计算即可;
(2)由导数的定义计算即可.
【详解】(1),
故当,时,,.
(2)由(1)得,
故函数在处的导数是48.
19.(1);
(2)0.35 m/s.
【分析】(1)根据题设,利用相似比,列方程即可得关系式;
(2)根据(1)所得关系,分别求出区间内对应自变量、函数值的增量,即可得平均变化率.
【详解】(1)如题图,设人从C点运动到B点位移为x m,AB为身影长度,为y m,
由于,则,即,所以.
(2)设人离开C点的时间为t s,而,而,所以.
在内自变量的增量为,
函数值的增量为,
所以.
即人离开C点10 s内身影长度的平均变化率为 m/s.
20.(1)
(2)存在;
【分析】(1)根据导数的几何意义求解;
(2)总有,即直线与直线的倾斜角互补,即恒有,联立直线与抛物线方程,得到韦达定理代入运算,判断得解.
【详解】(1)由已知,得,因为,所以,斜率,
因此,切线方程为,即.
(2)存在符合题意的点,理由如下:
设点为符合题意的点,,直线的斜率分别为.
联立方程,得,
因为,则,可得,
从而
,
因为不恒为0,可知当且仅当时,恒有,
则直线与直线的倾斜角互补,故,
所以点符合题意.
21.答案见解析
【分析】计算从处到处高度的平均变化率,从处到处高度的平均变化率,再比较两值的大小说明吃力的原因.
【详解】山路从A处到B处高度的平均变化率为,
山路从C处到D处高度的平均变化率为,
由知,山路从C处到D处比从A处到B处陡峭.
故从A处到B处会感觉比较轻松,而从C处到D处会感觉比较吃力.
答案第1页,共2页
答案第1页,共2页
