6.1.11 练习十七 课件-人教版数学六年级下册(共20张PPT)
文档属性
| 名称 | 6.1.11 练习十七 课件-人教版数学六年级下册(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第11课时 练习十七
第六单元 整理和复习
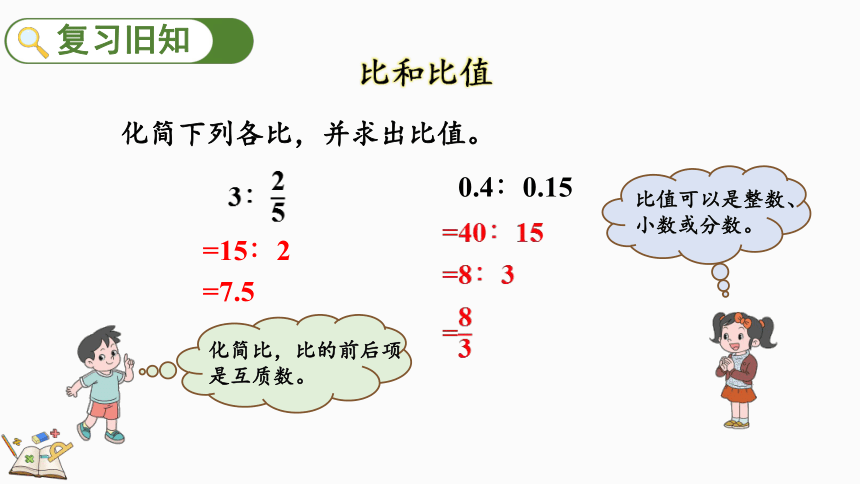
比和比值
化简下列各比,并求出比值。
=15∶2
=7.5
=40∶15
=8∶3
=
3∶
0.4∶0.15
比值可以是整数、小数或分数。
化简比,比的前后项是互质数。
解比例
解:0.9x = 5.4
x = 6
运用比例的基本性质。
=
1∶ =
解:x = ×
x =
(3)小丽的脚长23cm,她的身高是161cm,她的脚长与
身高之比为 。
(1)六年级男生有80人,女生有84人,男生与女生人数
之比为 。
1
选自教材第84页练习十七1~6题
20:21
1:1
1:7
5:3
(2)小明身高160 cm,他一庹长也是160 cm,二者之比
为 。
(4)如果3a=5b(a、b≠0),那么a:b= 。
判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知=3,y与x。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知xy =1,y与x。
(6)出油率一定,花生油的质量与花生的质量。
不成比例
成正比例关系
成反比例关系
成正比例关系
成反比例关系
成正比例关系
2
妈妈和面做面条,一共做了1.8kg,面粉和水的质量比是7:2。面粉和水分别用了多少千克?
3
7+2=9
面条中7份是面粉,2份是水。
1.8×=0.4(千克)
1.8×=1.4(千克)
答:面粉用了1.4千克,水用了0.4千克。
一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3:206,做302块这样的金牌需要黄金多少克?
4
根据黄金与金牌质量的比,可以列正比例解决问题。
解:设做302块这样的金牌需要黄金x克。
206x=373272
x:412×302=3:206
答:做302块这样的金牌需要黄金1812克。
x=1812
甲地到乙地的高速公路大约长200 km,乙地到丙地的高速公路大约长280 km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时?
5
速度一定,列正比例解答。
解:该车从甲地到丙地大约需要x小时。
200x=1200
(200+280):x=200:2.5
答:该车从甲地到丙地大约需要6小时。
x=6
在同一幅地图上,量得甲、乙两地的距离是20 cm,甲、丙两地的距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少?
6
图上距离:实际距离=比例尺
1600km=160000000cm
96000000(cm)
12÷(20÷160000000)=
答:甲、丙两地的实际距离是960千米。
=960km
96000000cm
1.判断下列各题中的两种量是不是成比例,说说你的
理由。
(1)煤的总量一定,每天的烧煤量与烧的天数。
(4)飞机从北京飞往上海,飞行的速度与需要的时间。
(2)圆的周长和它的直径。
(3)学校计划植500棵树,已植的棵树与未植的棵树。
成反比例 每天的烧煤量×烧的天数=煤的总量(一定)
成正比例 圆的周长∶直径=圆周率(一定)
不成比例 已植的棵树+未植的棵树=总棵树(一定)
成反比例 速度×时间=总路程(一定)
2.填一填。
(1)如果3∶5的前项加上6,要使比值不变,后项应加上( )。
10
(2)1g的糖放入100g水中,糖和糖水的比是( )。
1∶101
糖+水=101g
=
+6
×3
9
比的基本性质
×3
15
15-5=10
3.
某鞋厂五月份生产的女鞋的双数与男鞋的比是5∶3,已知女鞋比男鞋多1000双,生产的男鞋有多少双?
1000÷(5-3)×3=1500(双)
答:生产的男鞋有1500双。
女鞋的双数占5份,男鞋的双数占3份。
多的2份正好是多了1000双,先求一份是多少,再乘3就得到男鞋的数量。
4.
修路队修一条公路,已经修的米数和未修的米数的比是1∶2,如果再修180m,正好完成一半,这条公路长多少米?
答:这条公路长1080米。
180÷( )
-
=180÷
=1080(米)
占全长的 。
占全长的 。
5.
(3+2)×2=10
40÷10=4(cm)
4×3=12(cm)
4×2=8(cm)
一个长方形,周长40cm,长和宽的比是3∶2。这个长方形的面积是多少?
先求出周长的总份数,再求每份,然后求长、宽,最后求面积。
12×8=96(cm2)
答:这个长方形的面积是96cm2。
长
宽
6.
修路队修一条全长6000米的公路,15天修完。照这样计算,要修一条长8000米的公路,需要多少天?
解:设需要x天。
6000x = 8000×15
x = 20
答:需要20天。
=
每天修的长度一定,公路的长度和修的天数成正比例。
7.
光明学校发起“圆贫困地区孩子一个读书梦”爱心捐书公益活动,短短一周时间,就收到了同学们捐赠的大量书籍。学校决定将书打包后邮寄,现要求每包内装书的本数相同,用这批书的打包了14份还多42本,剩下的书连同第一次余下的刚好又打包了11份。这批书共有多少本?
解:设这批书有x 本。
x =1800
答:这批书共有1800本。
=
这节课有什么收获呢?
1.两个数相除,又叫作两个数的比。
例如: 3÷4=3:4=
2.表示两个比相等的式子叫作比例。
例如:1:2=4:8=0.5
这节课有什么收获呢?
3.两种相关联的量,若比值一定,则成正比例;
若积一定,则成反比例;若比值和积都不一
定,则不成比例。
例如:当速度一定时,路程和速度成正比例;
当路程一定时,速度和时间成反比例。
1.从教材练习十七中选取;
2.从课时练中选取。
比: 3÷4=3:4=
比例:1:2=4:8=0.5
比值一定 成正比例
积一定 成反比例
第11课时 练习十七
第六单元 整理和复习
比和比值
化简下列各比,并求出比值。
=15∶2
=7.5
=40∶15
=8∶3
=
3∶
0.4∶0.15
比值可以是整数、小数或分数。
化简比,比的前后项是互质数。
解比例
解:0.9x = 5.4
x = 6
运用比例的基本性质。
=
1∶ =
解:x = ×
x =
(3)小丽的脚长23cm,她的身高是161cm,她的脚长与
身高之比为 。
(1)六年级男生有80人,女生有84人,男生与女生人数
之比为 。
1
选自教材第84页练习十七1~6题
20:21
1:1
1:7
5:3
(2)小明身高160 cm,他一庹长也是160 cm,二者之比
为 。
(4)如果3a=5b(a、b≠0),那么a:b= 。
判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知=3,y与x。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知xy =1,y与x。
(6)出油率一定,花生油的质量与花生的质量。
不成比例
成正比例关系
成反比例关系
成正比例关系
成反比例关系
成正比例关系
2
妈妈和面做面条,一共做了1.8kg,面粉和水的质量比是7:2。面粉和水分别用了多少千克?
3
7+2=9
面条中7份是面粉,2份是水。
1.8×=0.4(千克)
1.8×=1.4(千克)
答:面粉用了1.4千克,水用了0.4千克。
一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3:206,做302块这样的金牌需要黄金多少克?
4
根据黄金与金牌质量的比,可以列正比例解决问题。
解:设做302块这样的金牌需要黄金x克。
206x=373272
x:412×302=3:206
答:做302块这样的金牌需要黄金1812克。
x=1812
甲地到乙地的高速公路大约长200 km,乙地到丙地的高速公路大约长280 km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时?
5
速度一定,列正比例解答。
解:该车从甲地到丙地大约需要x小时。
200x=1200
(200+280):x=200:2.5
答:该车从甲地到丙地大约需要6小时。
x=6
在同一幅地图上,量得甲、乙两地的距离是20 cm,甲、丙两地的距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少?
6
图上距离:实际距离=比例尺
1600km=160000000cm
96000000(cm)
12÷(20÷160000000)=
答:甲、丙两地的实际距离是960千米。
=960km
96000000cm
1.判断下列各题中的两种量是不是成比例,说说你的
理由。
(1)煤的总量一定,每天的烧煤量与烧的天数。
(4)飞机从北京飞往上海,飞行的速度与需要的时间。
(2)圆的周长和它的直径。
(3)学校计划植500棵树,已植的棵树与未植的棵树。
成反比例 每天的烧煤量×烧的天数=煤的总量(一定)
成正比例 圆的周长∶直径=圆周率(一定)
不成比例 已植的棵树+未植的棵树=总棵树(一定)
成反比例 速度×时间=总路程(一定)
2.填一填。
(1)如果3∶5的前项加上6,要使比值不变,后项应加上( )。
10
(2)1g的糖放入100g水中,糖和糖水的比是( )。
1∶101
糖+水=101g
=
+6
×3
9
比的基本性质
×3
15
15-5=10
3.
某鞋厂五月份生产的女鞋的双数与男鞋的比是5∶3,已知女鞋比男鞋多1000双,生产的男鞋有多少双?
1000÷(5-3)×3=1500(双)
答:生产的男鞋有1500双。
女鞋的双数占5份,男鞋的双数占3份。
多的2份正好是多了1000双,先求一份是多少,再乘3就得到男鞋的数量。
4.
修路队修一条公路,已经修的米数和未修的米数的比是1∶2,如果再修180m,正好完成一半,这条公路长多少米?
答:这条公路长1080米。
180÷( )
-
=180÷
=1080(米)
占全长的 。
占全长的 。
5.
(3+2)×2=10
40÷10=4(cm)
4×3=12(cm)
4×2=8(cm)
一个长方形,周长40cm,长和宽的比是3∶2。这个长方形的面积是多少?
先求出周长的总份数,再求每份,然后求长、宽,最后求面积。
12×8=96(cm2)
答:这个长方形的面积是96cm2。
长
宽
6.
修路队修一条全长6000米的公路,15天修完。照这样计算,要修一条长8000米的公路,需要多少天?
解:设需要x天。
6000x = 8000×15
x = 20
答:需要20天。
=
每天修的长度一定,公路的长度和修的天数成正比例。
7.
光明学校发起“圆贫困地区孩子一个读书梦”爱心捐书公益活动,短短一周时间,就收到了同学们捐赠的大量书籍。学校决定将书打包后邮寄,现要求每包内装书的本数相同,用这批书的打包了14份还多42本,剩下的书连同第一次余下的刚好又打包了11份。这批书共有多少本?
解:设这批书有x 本。
x =1800
答:这批书共有1800本。
=
这节课有什么收获呢?
1.两个数相除,又叫作两个数的比。
例如: 3÷4=3:4=
2.表示两个比相等的式子叫作比例。
例如:1:2=4:8=0.5
这节课有什么收获呢?
3.两种相关联的量,若比值一定,则成正比例;
若积一定,则成反比例;若比值和积都不一
定,则不成比例。
例如:当速度一定时,路程和速度成正比例;
当路程一定时,速度和时间成反比例。
1.从教材练习十七中选取;
2.从课时练中选取。
比: 3÷4=3:4=
比例:1:2=4:8=0.5
比值一定 成正比例
积一定 成反比例
