6.1.7 练习十五 课件-人教版数学六年级下册(共23张PPT)
文档属性
| 名称 | 6.1.7 练习十五 课件-人教版数学六年级下册(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第7课时 练习十五
第六单元 整理和复习
运算符号的由来
“+”、“-”的由来:据说,当时有酒商在售出酒后,曾用横线标出酒桶里的存酒,而当桶里的酒又增加时,便用竖线条把原来画的横线划掉。于是就出现用以表示减少的“-”和用来表示增加的“+”。1489年,德国数学家魏德曼在他的著作中首先使用“+”、“-”这两个符号表示剩余和不足,直到1630年,才得到大家的公认。
“×”乘号,三百多年前英国著名数学家欧德莱最先使用的,他认为乘法是加法的一种特殊形式,于是他便把前人所发明的“×”转动45°角,这样乘号“×”也就面世了。“×”既表示了乘法与加法的关系,又表示了相乘的方法。除号“÷”,最初这个符号是作为减号在欧洲大陆流行,最早人们用“:”表示除或比,也有人用分数线“-”表示比,后来有人把二者结合起来就变成了“÷”。
四则运算的关系
加法
减法
乘法
除法
把两个(或几个)数合并成一个数的运算。
一个加数+另一个加数=和 一个加数=和-另一个加数
已知两个数的和与其中的一个加数,求另一个加数的运算。
被减数-减数=差 ;被减数-差=减数 ;减数+差=被减数
求相同加数和的简便运算。
一个因数×另一个因数=积 ; 积÷一个因数=另一个因数
已知两个因数的积与其中一个因数,求另一个因数的运算。
被除数÷除数=商 ;被除数÷商=除数;商×除数=被除数
相同点
不同点
整数、小数、分数的运算都遵循四则运算法则。
1.整数对齐数位就可以加减;小数要对齐数位和小数点后才可以加减;
分数通分后才可以加减。
2.整数直接乘除;小数乘法要按整数乘法法则计算,小数除法把除数转化整数后,再按整数除法法则计算;分数除法转化为分数乘法,先分子乘分子,分母乘分母,然后约分计算。
小组讨论:整数、分数、小数运算时,有什么不同?
整数、小数、分数运算
四则混合运算顺序
没有括号
先算乘除,后算加减;如果只含同级运算,则从左往右依次计算。
如果能用简便算法计算的,可以简算。
有括号的要先算括号里面的
举手回答:说一说四则运算的运算顺序。
27+68= 910-540= 18×40= 910÷70=
78-0.8= 3÷12= 6.3÷0.1= 36×25%=
3.48+6.52= 1.02-0.43= 0.25×0.8= 12.6÷3=
口算。
1
选自教材第78~79页练习十五1~13题
95
+ =
3- =
×=
÷=
370
720
13
77.2
0.25
63
9
3
2
10
0.59
0.2
4.2
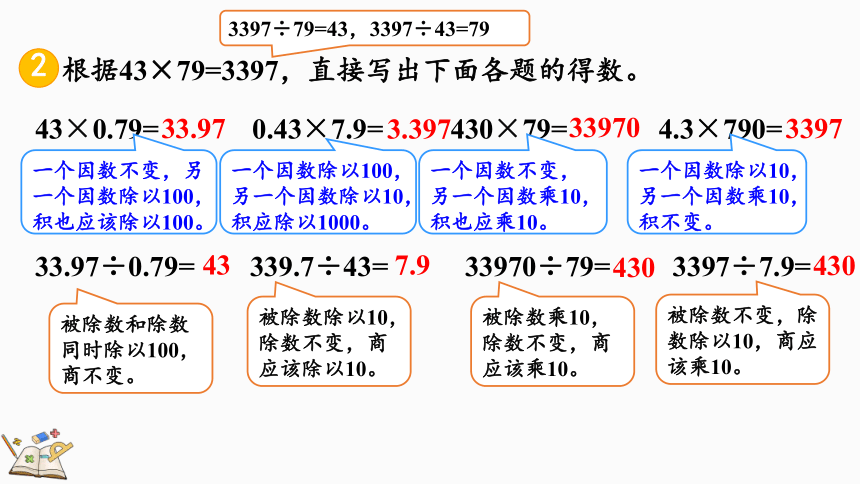
根据43×79=3397,直接写出下面各题的得数。
2
43×0.79= 0.43×7.9= 430×79= 4.3×790=
33.97÷0.79= 339.7÷43= 33970÷79= 3397÷7.9=
33.97
一个因数不变,另一个因数除以100,积也应该除以100。
被除数和除数同时除以100,商不变。
一个因数除以100,另一个因数除以10,积应除以1000。
3.397
一个因数不变,另一个因数乘10,积也应乘10。
一个因数除以10,另一个因数乘10,积不变。
33970
3397
43
被除数除以10,除数不变,商应该除以10。
7.9
被除数乘10,除数不变,商应该乘10。
430
被除数不变,除数除以10,商应该乘10。
430
3397÷79=43,3397÷43=79
803-207≈ 798+205≈
23×498≈ 632÷69≈
估算。
3
600
1000
10000
9
估算为800-200
估算为800+200
估算为20×500
估算为630÷70
估一估,在○里填上“>”或“<”。
4
5.9×9.9 60 32÷1.2 32 57×0.8 57
10.1×37 370
+
9
-
2.7
×
3
÷
1
<
<
<
>
>
>
>
<
计算。
=59×100+59×1
=5900+59
=5959
5
59×101 12.7-3.6-5.4
12.5×8÷12.5×8
=12.7-(3.6+5.4)
=12.7-9
=3.7
=12.5÷12.5×8×8
=8×8
=64
24×( + - )
=24× + 24× - 24×
=6+20-21
=5
=4×
=7
= ×[+ -]
×[-(- )]
= ×
=
用计算器计算左边一列题,你能发现什么规律?直接写出右边一列题的得数。
6
9×9-1= 98765×9-5=
98×9-2= 987654×9-6=
987×9-3= 9876543×9-7=
9876×9-4= 98765432×9-8=
80
发现:第一个因数排列规律一样,第二个因数都是9,减去几,积就是几个8和一个0组成。
880
8880
88880
888880
8888880
88888880
888888880
已知x+ = y+ = z+ ,
那么x、y、z的大小关系是( )<( )<( )。
7
因为三个算式得数相等,所以比较三个分数的大小,就可以知道三个字母的大小了,即字母加上的数越大,字母表示的数就越小。
x y z
六年级办公室买进一包白纸,计划每天用25 张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天
8
求实际比计划多用多少天
÷
实际用了多少天
原计划用了多少天
-
实际每天用多少张
一包白纸多少张
计划用的天数
计划每天用多少张
×
25×20÷20-20
=500÷20-20
=25-20
=5(天)
答:实际比计划多用5天。
一个旅游景点去年全年接待游客约196万人,上半年接待游客数是全年的 。第三季度接待游客数是上半年的 ,第三季度接待游客多少人
9
答:第三季度接待游客630000人。
196× × =63(万人)
63万=630000
全年人数× × 即可解答。
一种食用油,原来每升售价为12元。现在由于成本提高,单价提高了25%。原来买10L的钱,现在能买多少升
10
12×(1+25%)=15(元)
12×10÷15=8(L)
答:现在能买8 L。
比原来多25%。
也就是现在每升食用油的售价是原来的(1+25%)。
小明一家三口开车从北京去560km外的爷爷家。汽车每100 km耗油8L,按照这个耗油量,出发时加满60L汽油,中途不加油能到达爷爷家吗
11
方法一
跑560km的耗油量与60L汽油进行比较。
560÷100×8
=5.6×8
=44.8(L)
方法二
60L汽油跑的路程与560km进行比较。
60÷8×100
=7.5×100
=750(km)
44.8<60
750>560
答:能到达爷爷家。
答:能到达爷爷家。
下表是2022年11月1日G121次列车途经站点的相关信息。你能估算一下这趟列车在行驶全程中(扣除停留时间)的平均速度大约是多少吗
12
平均速度=总路程÷总时间
总时间:15时42分-10时05分=5时37分
停留总时间:2+4+2+2+2+2+6=20(分)
实际用时:5时37分-20分=5时17分≈5.28时
1318÷5.28 ≈249.62 (千米/时)
答:这趟列车在行驶全程中(扣除停留时间)的平均速度大约是249.62千米/时。
小红家客厅的顶灯需要更换一个灯泡。已知灯泡距地面2.6m,爸爸身高1.80m,小红搬来一个高0.6m的凳子。这能帮助爸爸成功更换灯泡吗?
1.8+0.6=2.4(米)
2.6-2.4=0.2(米)
答:这能帮助爸爸成功更换灯泡。
正常成年人的手臂长度一定大于0.2米
13
先求出爸爸站在凳子上的高度,再求距离灯泡高度,与手臂长度相比即可。
1.估算得数大约是多少,在□里画 “√”。
298+405 (600 □ 700 □ 800 □)
802-396 (400 □ 500 □ 600 □)
38 × 51 (1500 □ 2400 □ 2000 □)
√
√
√
2.长江发源于“世界屋脊”——青藏高原的唐古拉山脉各拉丹冬峰西南侧。在世界大河中居第三位。全长约6300千米,其中中游段占全长的,沱沱河的长度约是长江中游段的,沱沱河有多长?
6300× ×
=1000×
=380(千米)
答:沱沱河长380千米。
这节课有什么收获呢?
1.知道四则运算之间的关系,并能正确计算。
2.体会数学思想方法。
3.采取合适的运用策略,提高运算能力。
1.从教材练习十五中选取;
2.从课时练中选取。
加法
减法
乘法
除法
一个加数+另一个加数=和
一个加数=和-另一个加数
被减数-减数=差
被减数-差=减数
减数+差=被减数
一个因数×另一个因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
第7课时 练习十五
第六单元 整理和复习
运算符号的由来
“+”、“-”的由来:据说,当时有酒商在售出酒后,曾用横线标出酒桶里的存酒,而当桶里的酒又增加时,便用竖线条把原来画的横线划掉。于是就出现用以表示减少的“-”和用来表示增加的“+”。1489年,德国数学家魏德曼在他的著作中首先使用“+”、“-”这两个符号表示剩余和不足,直到1630年,才得到大家的公认。
“×”乘号,三百多年前英国著名数学家欧德莱最先使用的,他认为乘法是加法的一种特殊形式,于是他便把前人所发明的“×”转动45°角,这样乘号“×”也就面世了。“×”既表示了乘法与加法的关系,又表示了相乘的方法。除号“÷”,最初这个符号是作为减号在欧洲大陆流行,最早人们用“:”表示除或比,也有人用分数线“-”表示比,后来有人把二者结合起来就变成了“÷”。
四则运算的关系
加法
减法
乘法
除法
把两个(或几个)数合并成一个数的运算。
一个加数+另一个加数=和 一个加数=和-另一个加数
已知两个数的和与其中的一个加数,求另一个加数的运算。
被减数-减数=差 ;被减数-差=减数 ;减数+差=被减数
求相同加数和的简便运算。
一个因数×另一个因数=积 ; 积÷一个因数=另一个因数
已知两个因数的积与其中一个因数,求另一个因数的运算。
被除数÷除数=商 ;被除数÷商=除数;商×除数=被除数
相同点
不同点
整数、小数、分数的运算都遵循四则运算法则。
1.整数对齐数位就可以加减;小数要对齐数位和小数点后才可以加减;
分数通分后才可以加减。
2.整数直接乘除;小数乘法要按整数乘法法则计算,小数除法把除数转化整数后,再按整数除法法则计算;分数除法转化为分数乘法,先分子乘分子,分母乘分母,然后约分计算。
小组讨论:整数、分数、小数运算时,有什么不同?
整数、小数、分数运算
四则混合运算顺序
没有括号
先算乘除,后算加减;如果只含同级运算,则从左往右依次计算。
如果能用简便算法计算的,可以简算。
有括号的要先算括号里面的
举手回答:说一说四则运算的运算顺序。
27+68= 910-540= 18×40= 910÷70=
78-0.8= 3÷12= 6.3÷0.1= 36×25%=
3.48+6.52= 1.02-0.43= 0.25×0.8= 12.6÷3=
口算。
1
选自教材第78~79页练习十五1~13题
95
+ =
3- =
×=
÷=
370
720
13
77.2
0.25
63
9
3
2
10
0.59
0.2
4.2
根据43×79=3397,直接写出下面各题的得数。
2
43×0.79= 0.43×7.9= 430×79= 4.3×790=
33.97÷0.79= 339.7÷43= 33970÷79= 3397÷7.9=
33.97
一个因数不变,另一个因数除以100,积也应该除以100。
被除数和除数同时除以100,商不变。
一个因数除以100,另一个因数除以10,积应除以1000。
3.397
一个因数不变,另一个因数乘10,积也应乘10。
一个因数除以10,另一个因数乘10,积不变。
33970
3397
43
被除数除以10,除数不变,商应该除以10。
7.9
被除数乘10,除数不变,商应该乘10。
430
被除数不变,除数除以10,商应该乘10。
430
3397÷79=43,3397÷43=79
803-207≈ 798+205≈
23×498≈ 632÷69≈
估算。
3
600
1000
10000
9
估算为800-200
估算为800+200
估算为20×500
估算为630÷70
估一估,在○里填上“>”或“<”。
4
5.9×9.9 60 32÷1.2 32 57×0.8 57
10.1×37 370
+
9
-
2.7
×
3
÷
1
<
<
<
>
>
>
>
<
计算。
=59×100+59×1
=5900+59
=5959
5
59×101 12.7-3.6-5.4
12.5×8÷12.5×8
=12.7-(3.6+5.4)
=12.7-9
=3.7
=12.5÷12.5×8×8
=8×8
=64
24×( + - )
=24× + 24× - 24×
=6+20-21
=5
=4×
=7
= ×[+ -]
×[-(- )]
= ×
=
用计算器计算左边一列题,你能发现什么规律?直接写出右边一列题的得数。
6
9×9-1= 98765×9-5=
98×9-2= 987654×9-6=
987×9-3= 9876543×9-7=
9876×9-4= 98765432×9-8=
80
发现:第一个因数排列规律一样,第二个因数都是9,减去几,积就是几个8和一个0组成。
880
8880
88880
888880
8888880
88888880
888888880
已知x+ = y+ = z+ ,
那么x、y、z的大小关系是( )<( )<( )。
7
因为三个算式得数相等,所以比较三个分数的大小,就可以知道三个字母的大小了,即字母加上的数越大,字母表示的数就越小。
x y z
六年级办公室买进一包白纸,计划每天用25 张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天
8
求实际比计划多用多少天
÷
实际用了多少天
原计划用了多少天
-
实际每天用多少张
一包白纸多少张
计划用的天数
计划每天用多少张
×
25×20÷20-20
=500÷20-20
=25-20
=5(天)
答:实际比计划多用5天。
一个旅游景点去年全年接待游客约196万人,上半年接待游客数是全年的 。第三季度接待游客数是上半年的 ,第三季度接待游客多少人
9
答:第三季度接待游客630000人。
196× × =63(万人)
63万=630000
全年人数× × 即可解答。
一种食用油,原来每升售价为12元。现在由于成本提高,单价提高了25%。原来买10L的钱,现在能买多少升
10
12×(1+25%)=15(元)
12×10÷15=8(L)
答:现在能买8 L。
比原来多25%。
也就是现在每升食用油的售价是原来的(1+25%)。
小明一家三口开车从北京去560km外的爷爷家。汽车每100 km耗油8L,按照这个耗油量,出发时加满60L汽油,中途不加油能到达爷爷家吗
11
方法一
跑560km的耗油量与60L汽油进行比较。
560÷100×8
=5.6×8
=44.8(L)
方法二
60L汽油跑的路程与560km进行比较。
60÷8×100
=7.5×100
=750(km)
44.8<60
750>560
答:能到达爷爷家。
答:能到达爷爷家。
下表是2022年11月1日G121次列车途经站点的相关信息。你能估算一下这趟列车在行驶全程中(扣除停留时间)的平均速度大约是多少吗
12
平均速度=总路程÷总时间
总时间:15时42分-10时05分=5时37分
停留总时间:2+4+2+2+2+2+6=20(分)
实际用时:5时37分-20分=5时17分≈5.28时
1318÷5.28 ≈249.62 (千米/时)
答:这趟列车在行驶全程中(扣除停留时间)的平均速度大约是249.62千米/时。
小红家客厅的顶灯需要更换一个灯泡。已知灯泡距地面2.6m,爸爸身高1.80m,小红搬来一个高0.6m的凳子。这能帮助爸爸成功更换灯泡吗?
1.8+0.6=2.4(米)
2.6-2.4=0.2(米)
答:这能帮助爸爸成功更换灯泡。
正常成年人的手臂长度一定大于0.2米
13
先求出爸爸站在凳子上的高度,再求距离灯泡高度,与手臂长度相比即可。
1.估算得数大约是多少,在□里画 “√”。
298+405 (600 □ 700 □ 800 □)
802-396 (400 □ 500 □ 600 □)
38 × 51 (1500 □ 2400 □ 2000 □)
√
√
√
2.长江发源于“世界屋脊”——青藏高原的唐古拉山脉各拉丹冬峰西南侧。在世界大河中居第三位。全长约6300千米,其中中游段占全长的,沱沱河的长度约是长江中游段的,沱沱河有多长?
6300× ×
=1000×
=380(千米)
答:沱沱河长380千米。
这节课有什么收获呢?
1.知道四则运算之间的关系,并能正确计算。
2.体会数学思想方法。
3.采取合适的运用策略,提高运算能力。
1.从教材练习十五中选取;
2.从课时练中选取。
加法
减法
乘法
除法
一个加数+另一个加数=和
一个加数=和-另一个加数
被减数-减数=差
被减数-差=减数
减数+差=被减数
一个因数×另一个因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
