第八章 专题强化 功能关系及其应用 学案(学生版+教师版)—2024年春高中物理人教版必修二
文档属性
| 名称 | 第八章 专题强化 功能关系及其应用 学案(学生版+教师版)—2024年春高中物理人教版必修二 | 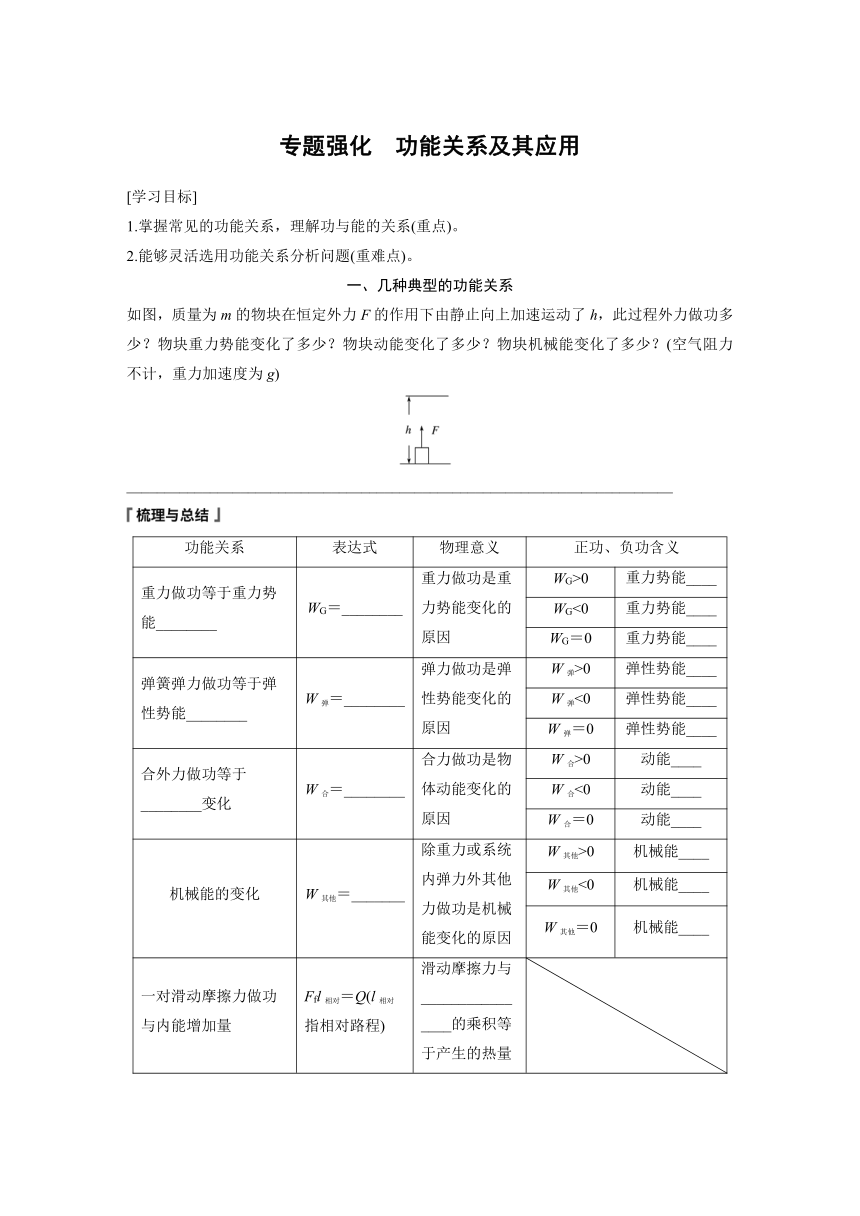 | |
| 格式 | docx | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-23 21:31:05 | ||
图片预览




文档简介
专题强化 功能关系及其应用
[学习目标]
1.掌握常见的功能关系,理解功与能的关系(重点)。
2.能够灵活选用功能关系分析问题(重难点)。
一、几种典型的功能关系
如图,质量为m的物块在恒定外力F的作用下由静止向上加速运动了h,此过程外力做功多少?物块重力势能变化了多少?物块动能变化了多少?物块机械能变化了多少?(空气阻力不计,重力加速度为g)
________________________________________________________________________
功能关系 表达式 物理意义 正功、负功含义
重力做功等于重力势能________ WG=________ 重力做功是重力势能变化的原因 WG>0 重力势能____
WG<0 重力势能____
WG=0 重力势能____
弹簧弹力做功等于弹性势能________ W弹=________ 弹力做功是弹性势能变化的原因 W弹>0 弹性势能____
W弹<0 弹性势能____
W弹=0 弹性势能____
合外力做功等于________变化 W合=________ 合力做功是物体动能变化的原因 W合>0 动能____
W合<0 动能____
W合=0 动能____
机械能的变化 W其他=_______ 除重力或系统内弹力外其他力做功是机械能变化的原因 W其他>0 机械能____
W其他<0 机械能____
W其他=0 机械能____
一对滑动摩擦力做功与内能增加量 Ffl相对=Q(l相对指相对路程) 滑动摩擦力与________________的乘积等于产生的热量
功和能一样吗?二者有何关系?
________________________________________________________________________
例1 质量为m的物体在升降机中,随升降机竖直向上以大小为g(g为重力加速度)的加速度做匀减速直线运动,上升高度为h,在此过程中,物体的机械能( )
A.增加mgh B.减少mgh
C.增加mgh D.减少mgh
例2 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(可视为质点)自A点的正上方P点由静止开始自由下落,小球沿圆弧轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,忽略空气阻力,则小球从P到B的运动过程中( )
A.重力做功2mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功mgR
二、热量的产生与摩擦力做功
如图,质量为M、长为l0的木板静止放置于光滑地面上,一质量为m的物块以速度v0从左端冲上木板,物块和木板间的滑动摩擦力大小为Ff。当物块滑至木板最右端时,两者恰好达到共同速度v,且此时木板位移为l。
(1)此过程中物块的位移大小为多少?对物块列出动能定理表达式。
(2)对木板列出动能定理的表达式。
(3)一对摩擦力对系统做的功为多少?(用Ff、l0表示);系统动能变化量为多少?(用M、m、v0、v表示);系统摩擦力做功的过程中产生的热量是多少?(用M、m、v0、v表示),产生的热量与一对滑动摩擦力对系统做功的大小相等吗?这说明什么?
________________________________________________________________________
________________________________________________________________________
例3 如图所示,质量为m0、长度为l的小车静止在光滑的水平面上。质量为m的小物块(可视为质点)放在小车的最左端。现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力大小为Ff。经过时间t,小车运动的位移为x,物块刚好滑到小车的最右端( )
A.此时物块的动能为F(x+l)
B.这一过程中,物块对小车所做的功为Ff(x+l)
C.这一过程中,物块和小车增加的机械能为Fx
D.这一过程中,物块和小车产生的热量为Ffl
例4 如图,木块静止在光滑水平桌面上,一子弹(可视为质点)水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿水平桌面移动的距离为x,木块对子弹的平均阻力大小为Ff,那么在这个过程中,下列说法不正确的是( )
A.木块的动能增量为Ffx
B.子弹的动能减少量为Ff(x+d)
C.系统的机械能减少量为Ffd
D.系统产生的热量为Ff(x+d)
专题强化 功能关系及其应用
[学习目标]
1.掌握常见的功能关系,理解功与能的关系(重点)。
2.能够灵活选用功能关系分析问题(重难点)。
一、几种典型的功能关系
如图,质量为m的物块在恒定外力F的作用下由静止向上加速运动了h,此过程外力做功多少?物块重力势能变化了多少?物块动能变化了多少?物块机械能变化了多少?(空气阻力不计,重力加速度为g)
答案 由功的定义,知此过程外力做功Fh
物块重力势能增加了mgh
对物块在此过程,由动能定理有Fh-mgh=mv2-0
则ΔEk=(F-mg)h
物块机械能变化量ΔE=mv2+mgh
故ΔE=Fh。
功能关系 表达式 物理意义 正功、负功含义
重力做功等于重力势能减少量 WG=-ΔEp 重力做功是重力势能变化的原因 WG>0 重力势能减少
WG<0 重力势能增加
WG=0 重力势能不变
弹簧弹力做功等于弹性势能减少量 W弹=-ΔEp 弹力做功是弹性势能变化的原因 W弹>0 弹性势能减少
W弹<0 弹性势能增加
W弹=0 弹性势能不变
合外力做功等于动能变化 W合=ΔEk 合力做功是物体动能变化的原因 W合>0 动能增加
W合<0 动能减少
W合=0 动能不变
机械能的变化 W其他=ΔE机 除重力或系统内弹力外其他力做功是机械能变化的原因 W其他>0 机械能增加
W其他<0 机械能减少
W其他=0 机械能守恒
一对滑动摩擦力做功与内能增加量 Ffl相对=Q(l相对指相对路程) 滑动摩擦力与相对路程的乘积等于产生的热量
功和能一样吗?二者有何关系?
答案 不一样。二者的关系:
①功是能量转化的量度。
②力的做功过程就是能量转化的过程;不同的力做功,对应不同形式的能的转化。
③做功的多少与能量转化的多少在数值上相等。
例1 质量为m的物体在升降机中,随升降机竖直向上以大小为g(g为重力加速度)的加速度做匀减速直线运动,上升高度为h,在此过程中,物体的机械能( )
A.增加mgh B.减少mgh
C.增加mgh D.减少mgh
答案 C
解析 物体减速上升,加速度方向向下,由牛顿第二定律可得mg-F=ma,解得F=mg,除重力外的其他力所做的功等于机械能的变化量,力F做正功,机械能增加,增加量为ΔE=Fh=mgh,故选C。
例2 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(可视为质点)自A点的正上方P点由静止开始自由下落,小球沿圆弧轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,忽略空气阻力,则小球从P到B的运动过程中( )
A.重力做功2mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功mgR
答案 B
解析 P、B高度差为R,重力做功为mgR,A错误;到达最高点B时恰好对轨道没有压力,则mg=m,得vB=,所以合外力做功W=mvB2=mgR,C错误;以OA所在平面为参考平面,初始机械能为E1=2mgR,末状态机械能为E2=mgR+mvB2,机械能增量为ΔE=E2-E1=-mgR,则W克f=mgR,B正确,D错误。
二、热量的产生与摩擦力做功
如图,质量为M、长为l0的木板静止放置于光滑地面上,一质量为m的物块以速度v0从左端冲上木板,物块和木板间的滑动摩擦力大小为Ff。当物块滑至木板最右端时,两者恰好达到共同速度v,且此时木板位移为l。
(1)此过程中物块的位移大小为多少?对物块列出动能定理表达式。
(2)对木板列出动能定理的表达式。
(3)一对摩擦力对系统做的功为多少?(用Ff、l0表示);系统动能变化量为多少?(用M、m、v0、v表示);系统摩擦力做功的过程中产生的热量是多少?(用M、m、v0、v表示),产生的热量与一对滑动摩擦力对系统做功的大小相等吗?这说明什么?
答案 (1)物块位移大小x=l+l0,由动能定理
-Ff(l+l0)=mv2-mv02①
(2)Ffl=Mv2②
(3)由①②式相加
-Ff(l+l0)+Ffl=mv2+Mv2-mv02③
即-Ffl0=mv2+Mv2-mv02④
一对摩擦力对系统做功为-Ffl0
系统动能变化量为mv2+Mv2-mv02
系统摩擦力做功过程中产生的热量
Q=mv02-(mv2+Mv2)
由④式知,摩擦力做功产生的热量与一对滑动摩擦力对系统做功的大小相等,故有Ffl相对=Q(l相对指相对路程)。
例3 如图所示,质量为m0、长度为l的小车静止在光滑的水平面上。质量为m的小物块(可视为质点)放在小车的最左端。现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力大小为Ff。经过时间t,小车运动的位移为x,物块刚好滑到小车的最右端( )
A.此时物块的动能为F(x+l)
B.这一过程中,物块对小车所做的功为Ff(x+l)
C.这一过程中,物块和小车增加的机械能为Fx
D.这一过程中,物块和小车产生的热量为Ffl
答案 D
解析 对物块分析,物块的位移为x+l,根据动能定理得(F-Ff)(x+l)=Ek-0,所以物块到达小车最右端时的动能为(F-Ff)(x+l),故A错误;对小车分析,小车的位移为x,所以物块对小车所做的功为Ffx,故B错误;物块和小车产生的热量Q=Ffs相对=Ffl,故D正确;根据功能关系得,外力F做的功转化为小车和物块的机械能和摩擦产生的内能,则有F(l+x)=ΔE+Q,则ΔE=F(l+x)-Ffl,故C错误。
例4 如图,木块静止在光滑水平桌面上,一子弹(可视为质点)水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿水平桌面移动的距离为x,木块对子弹的平均阻力大小为Ff,那么在这个过程中,下列说法不正确的是( )
A.木块的动能增量为Ffx
B.子弹的动能减少量为Ff(x+d)
C.系统的机械能减少量为Ffd
D.系统产生的热量为Ff(x+d)
答案 D
解析 子弹对木块的作用力大小为Ff,木块相对于桌面的位移为x,则子弹对木块做功为Ffx,根据功能关系,木块动能的增量等于子弹对木块做的功,即为Ffx,故A正确;木块对子弹的阻力做功为 W=-Ff(x+d),根据功能关系得知:子弹动能的减少量等于子弹克服阻力做的功,大小为Ff(x+d),故B正确;子弹相对于木块的位移大小为d,则系统克服阻力做功为Ffd,根据功能关系可知,系统机械能的减少量为Ffd,产生的热量为Ffd,故C正确,D错误。
[学习目标]
1.掌握常见的功能关系,理解功与能的关系(重点)。
2.能够灵活选用功能关系分析问题(重难点)。
一、几种典型的功能关系
如图,质量为m的物块在恒定外力F的作用下由静止向上加速运动了h,此过程外力做功多少?物块重力势能变化了多少?物块动能变化了多少?物块机械能变化了多少?(空气阻力不计,重力加速度为g)
________________________________________________________________________
功能关系 表达式 物理意义 正功、负功含义
重力做功等于重力势能________ WG=________ 重力做功是重力势能变化的原因 WG>0 重力势能____
WG<0 重力势能____
WG=0 重力势能____
弹簧弹力做功等于弹性势能________ W弹=________ 弹力做功是弹性势能变化的原因 W弹>0 弹性势能____
W弹<0 弹性势能____
W弹=0 弹性势能____
合外力做功等于________变化 W合=________ 合力做功是物体动能变化的原因 W合>0 动能____
W合<0 动能____
W合=0 动能____
机械能的变化 W其他=_______ 除重力或系统内弹力外其他力做功是机械能变化的原因 W其他>0 机械能____
W其他<0 机械能____
W其他=0 机械能____
一对滑动摩擦力做功与内能增加量 Ffl相对=Q(l相对指相对路程) 滑动摩擦力与________________的乘积等于产生的热量
功和能一样吗?二者有何关系?
________________________________________________________________________
例1 质量为m的物体在升降机中,随升降机竖直向上以大小为g(g为重力加速度)的加速度做匀减速直线运动,上升高度为h,在此过程中,物体的机械能( )
A.增加mgh B.减少mgh
C.增加mgh D.减少mgh
例2 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(可视为质点)自A点的正上方P点由静止开始自由下落,小球沿圆弧轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,忽略空气阻力,则小球从P到B的运动过程中( )
A.重力做功2mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功mgR
二、热量的产生与摩擦力做功
如图,质量为M、长为l0的木板静止放置于光滑地面上,一质量为m的物块以速度v0从左端冲上木板,物块和木板间的滑动摩擦力大小为Ff。当物块滑至木板最右端时,两者恰好达到共同速度v,且此时木板位移为l。
(1)此过程中物块的位移大小为多少?对物块列出动能定理表达式。
(2)对木板列出动能定理的表达式。
(3)一对摩擦力对系统做的功为多少?(用Ff、l0表示);系统动能变化量为多少?(用M、m、v0、v表示);系统摩擦力做功的过程中产生的热量是多少?(用M、m、v0、v表示),产生的热量与一对滑动摩擦力对系统做功的大小相等吗?这说明什么?
________________________________________________________________________
________________________________________________________________________
例3 如图所示,质量为m0、长度为l的小车静止在光滑的水平面上。质量为m的小物块(可视为质点)放在小车的最左端。现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力大小为Ff。经过时间t,小车运动的位移为x,物块刚好滑到小车的最右端( )
A.此时物块的动能为F(x+l)
B.这一过程中,物块对小车所做的功为Ff(x+l)
C.这一过程中,物块和小车增加的机械能为Fx
D.这一过程中,物块和小车产生的热量为Ffl
例4 如图,木块静止在光滑水平桌面上,一子弹(可视为质点)水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿水平桌面移动的距离为x,木块对子弹的平均阻力大小为Ff,那么在这个过程中,下列说法不正确的是( )
A.木块的动能增量为Ffx
B.子弹的动能减少量为Ff(x+d)
C.系统的机械能减少量为Ffd
D.系统产生的热量为Ff(x+d)
专题强化 功能关系及其应用
[学习目标]
1.掌握常见的功能关系,理解功与能的关系(重点)。
2.能够灵活选用功能关系分析问题(重难点)。
一、几种典型的功能关系
如图,质量为m的物块在恒定外力F的作用下由静止向上加速运动了h,此过程外力做功多少?物块重力势能变化了多少?物块动能变化了多少?物块机械能变化了多少?(空气阻力不计,重力加速度为g)
答案 由功的定义,知此过程外力做功Fh
物块重力势能增加了mgh
对物块在此过程,由动能定理有Fh-mgh=mv2-0
则ΔEk=(F-mg)h
物块机械能变化量ΔE=mv2+mgh
故ΔE=Fh。
功能关系 表达式 物理意义 正功、负功含义
重力做功等于重力势能减少量 WG=-ΔEp 重力做功是重力势能变化的原因 WG>0 重力势能减少
WG<0 重力势能增加
WG=0 重力势能不变
弹簧弹力做功等于弹性势能减少量 W弹=-ΔEp 弹力做功是弹性势能变化的原因 W弹>0 弹性势能减少
W弹<0 弹性势能增加
W弹=0 弹性势能不变
合外力做功等于动能变化 W合=ΔEk 合力做功是物体动能变化的原因 W合>0 动能增加
W合<0 动能减少
W合=0 动能不变
机械能的变化 W其他=ΔE机 除重力或系统内弹力外其他力做功是机械能变化的原因 W其他>0 机械能增加
W其他<0 机械能减少
W其他=0 机械能守恒
一对滑动摩擦力做功与内能增加量 Ffl相对=Q(l相对指相对路程) 滑动摩擦力与相对路程的乘积等于产生的热量
功和能一样吗?二者有何关系?
答案 不一样。二者的关系:
①功是能量转化的量度。
②力的做功过程就是能量转化的过程;不同的力做功,对应不同形式的能的转化。
③做功的多少与能量转化的多少在数值上相等。
例1 质量为m的物体在升降机中,随升降机竖直向上以大小为g(g为重力加速度)的加速度做匀减速直线运动,上升高度为h,在此过程中,物体的机械能( )
A.增加mgh B.减少mgh
C.增加mgh D.减少mgh
答案 C
解析 物体减速上升,加速度方向向下,由牛顿第二定律可得mg-F=ma,解得F=mg,除重力外的其他力所做的功等于机械能的变化量,力F做正功,机械能增加,增加量为ΔE=Fh=mgh,故选C。
例2 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(可视为质点)自A点的正上方P点由静止开始自由下落,小球沿圆弧轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,忽略空气阻力,则小球从P到B的运动过程中( )
A.重力做功2mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功mgR
答案 B
解析 P、B高度差为R,重力做功为mgR,A错误;到达最高点B时恰好对轨道没有压力,则mg=m,得vB=,所以合外力做功W=mvB2=mgR,C错误;以OA所在平面为参考平面,初始机械能为E1=2mgR,末状态机械能为E2=mgR+mvB2,机械能增量为ΔE=E2-E1=-mgR,则W克f=mgR,B正确,D错误。
二、热量的产生与摩擦力做功
如图,质量为M、长为l0的木板静止放置于光滑地面上,一质量为m的物块以速度v0从左端冲上木板,物块和木板间的滑动摩擦力大小为Ff。当物块滑至木板最右端时,两者恰好达到共同速度v,且此时木板位移为l。
(1)此过程中物块的位移大小为多少?对物块列出动能定理表达式。
(2)对木板列出动能定理的表达式。
(3)一对摩擦力对系统做的功为多少?(用Ff、l0表示);系统动能变化量为多少?(用M、m、v0、v表示);系统摩擦力做功的过程中产生的热量是多少?(用M、m、v0、v表示),产生的热量与一对滑动摩擦力对系统做功的大小相等吗?这说明什么?
答案 (1)物块位移大小x=l+l0,由动能定理
-Ff(l+l0)=mv2-mv02①
(2)Ffl=Mv2②
(3)由①②式相加
-Ff(l+l0)+Ffl=mv2+Mv2-mv02③
即-Ffl0=mv2+Mv2-mv02④
一对摩擦力对系统做功为-Ffl0
系统动能变化量为mv2+Mv2-mv02
系统摩擦力做功过程中产生的热量
Q=mv02-(mv2+Mv2)
由④式知,摩擦力做功产生的热量与一对滑动摩擦力对系统做功的大小相等,故有Ffl相对=Q(l相对指相对路程)。
例3 如图所示,质量为m0、长度为l的小车静止在光滑的水平面上。质量为m的小物块(可视为质点)放在小车的最左端。现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力大小为Ff。经过时间t,小车运动的位移为x,物块刚好滑到小车的最右端( )
A.此时物块的动能为F(x+l)
B.这一过程中,物块对小车所做的功为Ff(x+l)
C.这一过程中,物块和小车增加的机械能为Fx
D.这一过程中,物块和小车产生的热量为Ffl
答案 D
解析 对物块分析,物块的位移为x+l,根据动能定理得(F-Ff)(x+l)=Ek-0,所以物块到达小车最右端时的动能为(F-Ff)(x+l),故A错误;对小车分析,小车的位移为x,所以物块对小车所做的功为Ffx,故B错误;物块和小车产生的热量Q=Ffs相对=Ffl,故D正确;根据功能关系得,外力F做的功转化为小车和物块的机械能和摩擦产生的内能,则有F(l+x)=ΔE+Q,则ΔE=F(l+x)-Ffl,故C错误。
例4 如图,木块静止在光滑水平桌面上,一子弹(可视为质点)水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿水平桌面移动的距离为x,木块对子弹的平均阻力大小为Ff,那么在这个过程中,下列说法不正确的是( )
A.木块的动能增量为Ffx
B.子弹的动能减少量为Ff(x+d)
C.系统的机械能减少量为Ffd
D.系统产生的热量为Ff(x+d)
答案 D
解析 子弹对木块的作用力大小为Ff,木块相对于桌面的位移为x,则子弹对木块做功为Ffx,根据功能关系,木块动能的增量等于子弹对木块做的功,即为Ffx,故A正确;木块对子弹的阻力做功为 W=-Ff(x+d),根据功能关系得知:子弹动能的减少量等于子弹克服阻力做的功,大小为Ff(x+d),故B正确;子弹相对于木块的位移大小为d,则系统克服阻力做功为Ffd,根据功能关系可知,系统机械能的减少量为Ffd,产生的热量为Ffd,故C正确,D错误。
