6.2.2 立体图形的认识与测量 (课件+教案)人教版数学六年级下册
文档属性
| 名称 | 6.2.2 立体图形的认识与测量 (课件+教案)人教版数学六年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 16:08:32 | ||
图片预览



文档简介
(共22张PPT)
第13课时 立体图形的认识与测量
第六单元 整理和复习
长方体、正方体都是立体图形。
我们学过哪些立体图形,它们有什么特征?
一起来复习这部分的知识吧。
立体图形的特征
立体图形 特 征
6个面是长方形(特殊情况有两个对面是正方形)相对的面完全相同;12条棱,相对的4条棱长度相等;8个顶点。
6个面都相等,都是正方形;12条棱都相等;8个顶点。
上下两个面是完全相同的圆形,侧面是一个曲面,沿高展开一般是个长方形。上下一样粗;有无数条高,每条高长度都相等。
底面是一个圆,侧面展开是扇形,有一个顶点,只有一条高。
这些立体图形各有什么特点
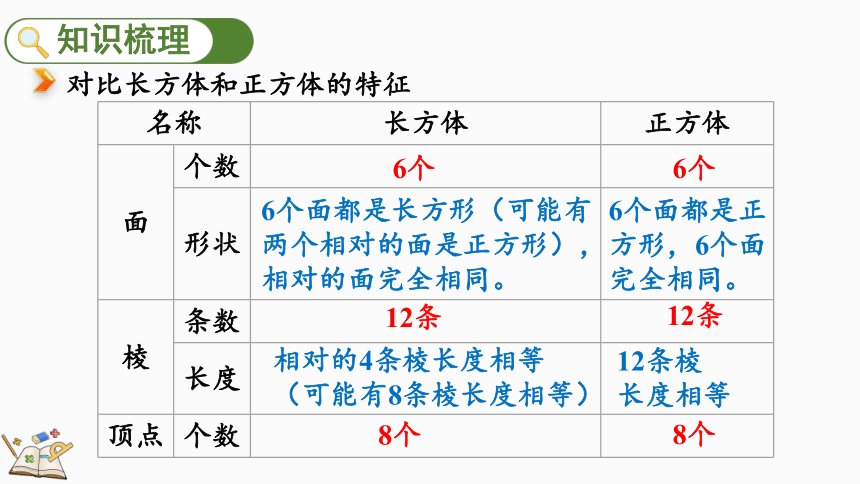
对比长方体和正方体的特征
名称 长方体 正方体
面 个数
形状
棱 条数
长度
顶点 个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱
长度相等
8个
8个
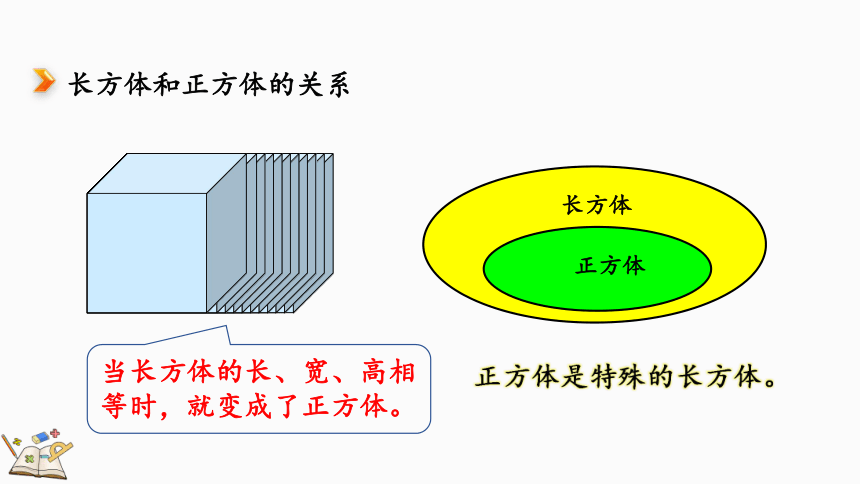
长方体和正方体的关系
正方体是特殊的长方体。
长方体
正方体
当长方体的长、宽、高相等时,就变成了正方体。
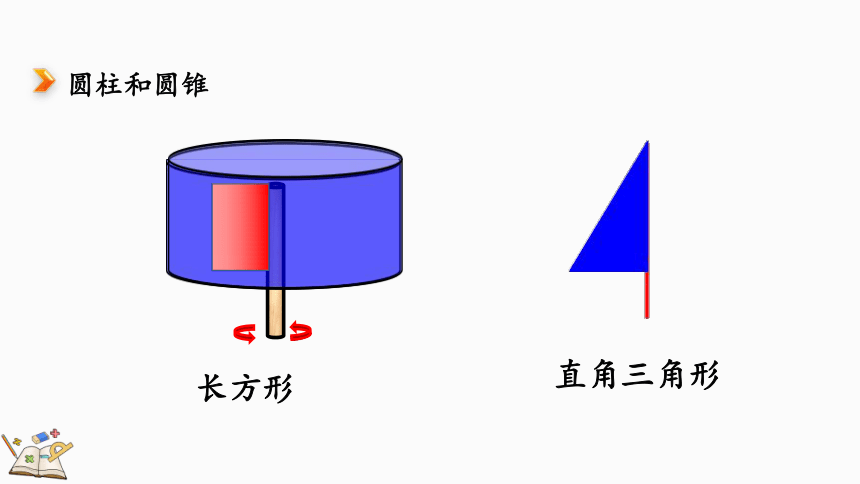
圆柱和圆锥
长方形
直角三角形
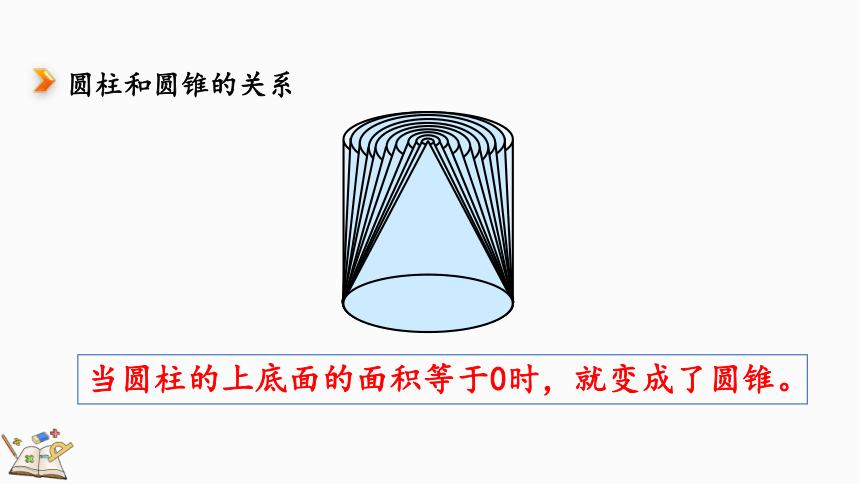
圆柱和圆锥的关系
当圆柱的上底面的面积等于0时,就变成了圆锥。
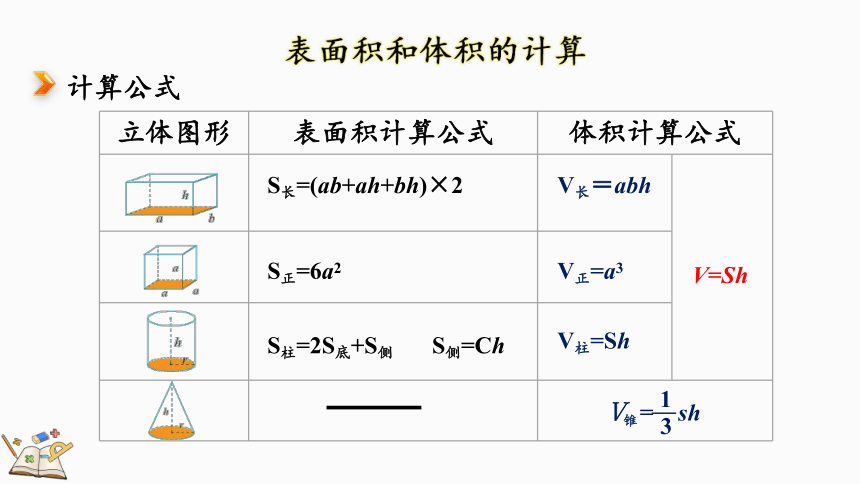
计算公式
立体图形 表面积计算公式 体积计算公式
S长=(ab+ah+bh)×2
S正=6a2
S柱=2S底+S侧 S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
表面积和体积的计算
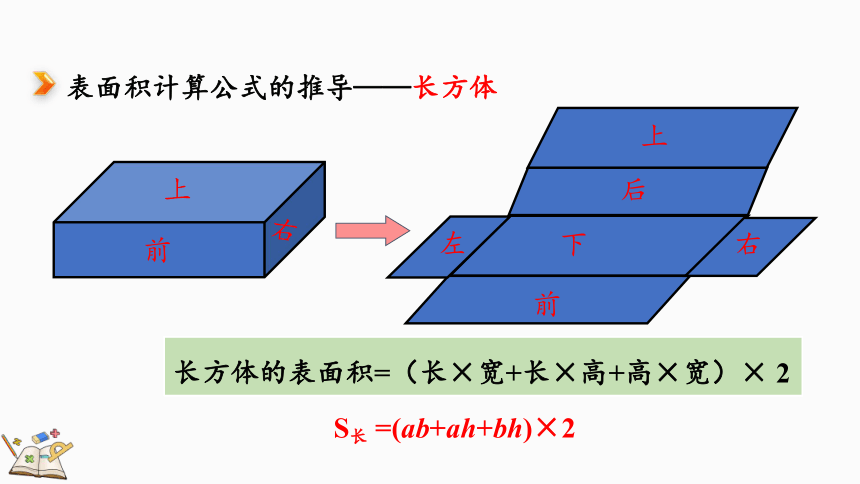
表面积计算公式的推导——长方体
上
前
右
长方体的表面积=(长×宽+长×高+高×宽)× 2
S长 =(ab+ah+bh)×2
上
下
前
后
左
右
表面积计算公式的推导——正方体
正方体的表面积=棱长×棱长×6
S正=6a2
上
下
后
左
右
表面积计算公式的推导——圆柱
底面
底面
圆柱的表面积=侧面积+两个底面的面积
侧 面
S表=2S底+S侧 S侧=Ch
体积计算公式的推导——长(正)方体
a厘米
b厘米
h
厘
米
长方体的体积 = 长×宽×高
V =ɑbh
长方体的体积 = 底面积×高
V = Sh
正方体是长宽高相等的长方体
所以V =ɑ
体积计算公式的推导——圆柱
底面积
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
V = Sh
高
高
体积计算公式的推导——圆锥
圆锥的体积等于与它等底等高圆柱体积的三分之一。
圆锥的体积= × 底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
选自教材第87页“做一做”第1题。
怎样测量出一块拳头大的鹅卵石的体积?
1
2cm
上升的水的体积就是鹅卵石的体积。
30cm
30cm
30 × 30 × 2
=900 × 2
=1800(立方厘米)
在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
2
正面 左面 上面
选自教材第87页“做一做”第2题。
1.
连一连。
2.
下面说法是否正确?对的画“√”,错的画“×”。
(1)长方体六个面一定是长方形。
(2)圆柱和圆锥的侧面展开都是长方形。
(3)正方体棱长总和是48厘米,它的每条棱长是4厘米。
(4)正方体的棱长扩大2倍,它的体积就扩大6倍。
(5)圆柱体的体积等于圆锥体的3倍。
( )
( )
( )
( )
( )
√
×
×
×
×
圆锥的侧面展开是一个扇形。
8倍
必须是等底等高的圆柱和圆锥。
3.
上海世博会上的中国馆——“东方之冠”,造型独特,令世人瞩目。它的顶层是由底部的四根巨型钢筋混凝土核心筒托起,每个核心筒的截面都是边长为18.6米的正方形,高68米。这四根核心筒的体积一共是多少立方米?
18.6×18.6×68×4
=94101.12(立方米)
答:一共是94101.12立方米。
4.
一个蓄水池(如下图),长10米,宽4米,深2米。
(1)蓄水池占地面积有多大?
(2)在蓄水池的底面和四周抹上水泥,抹水泥的面积有多大?
(3)蓄水池最多能蓄水多少立方米?
10×2×4 = 80(立方米)
10×4 = 40(平方米)
10×4 +(4×2+2×10)×2= 96(平方米)
答:抹水泥的面积是96平方米。
答:最多能蓄水80立方米。
答:占地面积是40平方米。
1.从教材总复习中选取;
2.从课时练中选取。
S长=(ab+ah+bh)×2
S正=6a2
S柱=2S底+S侧 S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
第13课时 立体图形的认识与测量
第六单元 整理和复习
长方体、正方体都是立体图形。
我们学过哪些立体图形,它们有什么特征?
一起来复习这部分的知识吧。
立体图形的特征
立体图形 特 征
6个面是长方形(特殊情况有两个对面是正方形)相对的面完全相同;12条棱,相对的4条棱长度相等;8个顶点。
6个面都相等,都是正方形;12条棱都相等;8个顶点。
上下两个面是完全相同的圆形,侧面是一个曲面,沿高展开一般是个长方形。上下一样粗;有无数条高,每条高长度都相等。
底面是一个圆,侧面展开是扇形,有一个顶点,只有一条高。
这些立体图形各有什么特点
对比长方体和正方体的特征
名称 长方体 正方体
面 个数
形状
棱 条数
长度
顶点 个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱
长度相等
8个
8个
长方体和正方体的关系
正方体是特殊的长方体。
长方体
正方体
当长方体的长、宽、高相等时,就变成了正方体。
圆柱和圆锥
长方形
直角三角形
圆柱和圆锥的关系
当圆柱的上底面的面积等于0时,就变成了圆锥。
计算公式
立体图形 表面积计算公式 体积计算公式
S长=(ab+ah+bh)×2
S正=6a2
S柱=2S底+S侧 S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
表面积和体积的计算
表面积计算公式的推导——长方体
上
前
右
长方体的表面积=(长×宽+长×高+高×宽)× 2
S长 =(ab+ah+bh)×2
上
下
前
后
左
右
表面积计算公式的推导——正方体
正方体的表面积=棱长×棱长×6
S正=6a2
上
下
后
左
右
表面积计算公式的推导——圆柱
底面
底面
圆柱的表面积=侧面积+两个底面的面积
侧 面
S表=2S底+S侧 S侧=Ch
体积计算公式的推导——长(正)方体
a厘米
b厘米
h
厘
米
长方体的体积 = 长×宽×高
V =ɑbh
长方体的体积 = 底面积×高
V = Sh
正方体是长宽高相等的长方体
所以V =ɑ
体积计算公式的推导——圆柱
底面积
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
V = Sh
高
高
体积计算公式的推导——圆锥
圆锥的体积等于与它等底等高圆柱体积的三分之一。
圆锥的体积= × 底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
选自教材第87页“做一做”第1题。
怎样测量出一块拳头大的鹅卵石的体积?
1
2cm
上升的水的体积就是鹅卵石的体积。
30cm
30cm
30 × 30 × 2
=900 × 2
=1800(立方厘米)
在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
2
正面 左面 上面
选自教材第87页“做一做”第2题。
1.
连一连。
2.
下面说法是否正确?对的画“√”,错的画“×”。
(1)长方体六个面一定是长方形。
(2)圆柱和圆锥的侧面展开都是长方形。
(3)正方体棱长总和是48厘米,它的每条棱长是4厘米。
(4)正方体的棱长扩大2倍,它的体积就扩大6倍。
(5)圆柱体的体积等于圆锥体的3倍。
( )
( )
( )
( )
( )
√
×
×
×
×
圆锥的侧面展开是一个扇形。
8倍
必须是等底等高的圆柱和圆锥。
3.
上海世博会上的中国馆——“东方之冠”,造型独特,令世人瞩目。它的顶层是由底部的四根巨型钢筋混凝土核心筒托起,每个核心筒的截面都是边长为18.6米的正方形,高68米。这四根核心筒的体积一共是多少立方米?
18.6×18.6×68×4
=94101.12(立方米)
答:一共是94101.12立方米。
4.
一个蓄水池(如下图),长10米,宽4米,深2米。
(1)蓄水池占地面积有多大?
(2)在蓄水池的底面和四周抹上水泥,抹水泥的面积有多大?
(3)蓄水池最多能蓄水多少立方米?
10×2×4 = 80(立方米)
10×4 = 40(平方米)
10×4 +(4×2+2×10)×2= 96(平方米)
答:抹水泥的面积是96平方米。
答:最多能蓄水80立方米。
答:占地面积是40平方米。
1.从教材总复习中选取;
2.从课时练中选取。
S长=(ab+ah+bh)×2
S正=6a2
S柱=2S底+S侧 S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
