6.2.3 练习十八 课件(共28张PPT) 人教版数学六年级下册
文档属性
| 名称 | 6.2.3 练习十八 课件(共28张PPT) 人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 16:10:35 | ||
图片预览



文档简介
(共28张PPT)
第14课时 练习十八
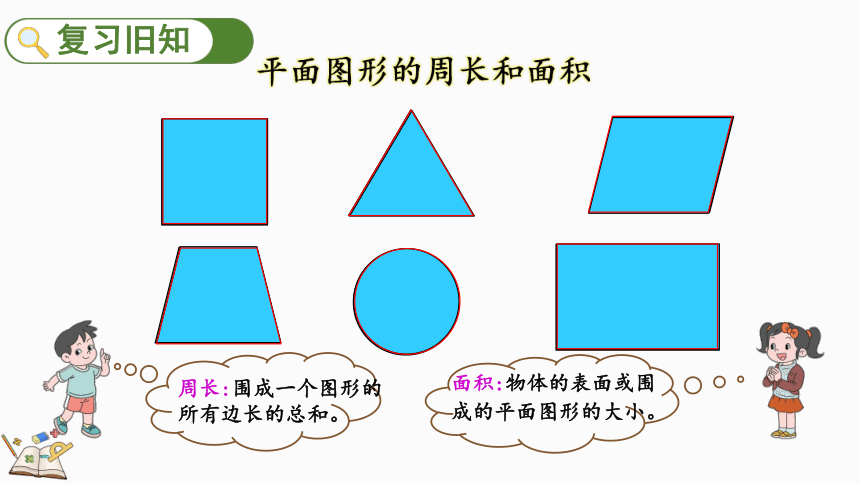
第六单元 整理和复面图形的周长和面积
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
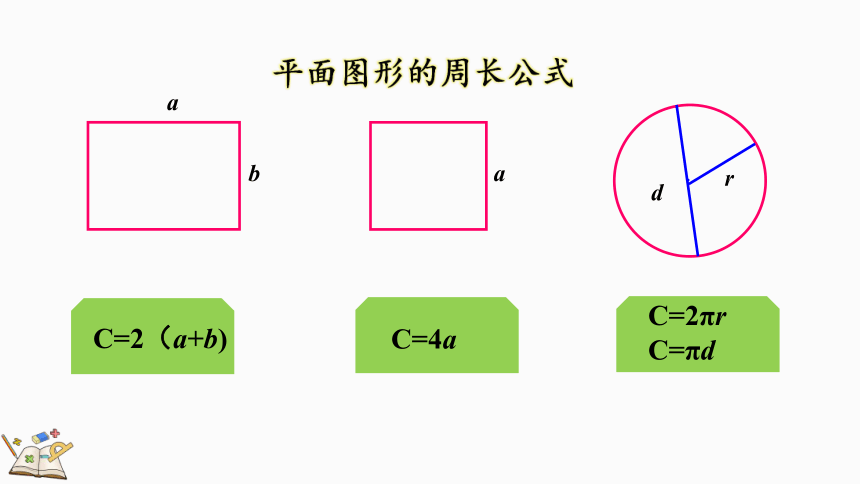
平面图形的周长公式
a
b
a
.
r
d
C=2(a+b)
C=4a
C=2πr
C=πd
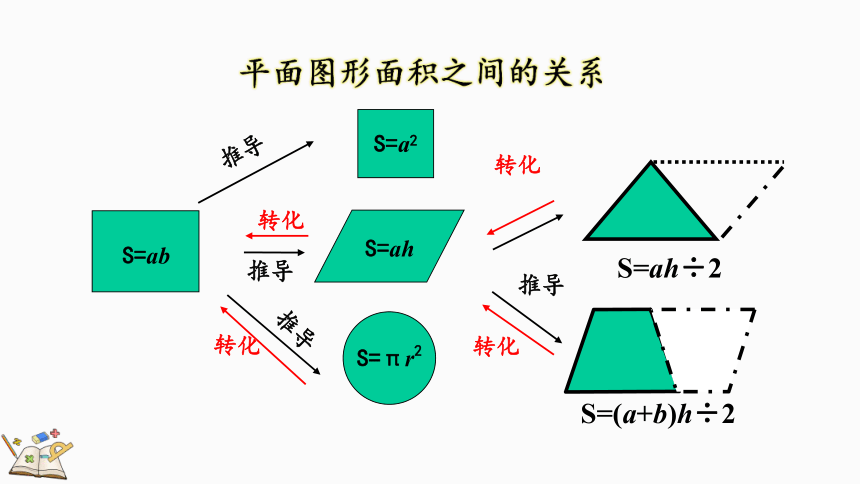
平面图形面积之间的关系
S=πr2
S=ab
S=ah
推导
转化
转化
推导
S=(a+b)h÷2
S=ah÷2
转化
S=a2
转化
推导
推导
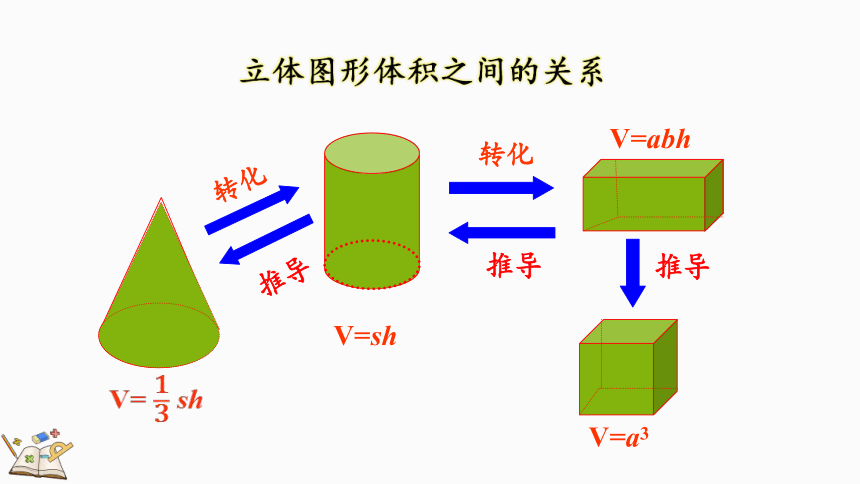
立体图形体积之间的关系
推导
转化
转化
推导
V=abh
V=a3
V=sh
V= sh
推导
判断下面的说法是否正确,并说一说你的理由。
(1)大于90°的角就是钝角。
(2)两条直线相交构成的4个角中如果有一个角是直角,那
么其他3个角也是直角。
(3)任何两个等底、等高的三角形都能拼成一个平行四边形。
1
选自教材第88~90页练习十八
错误,钝角是大于90°而小于180°的角。
正确,互相垂直的两条线,形成的四个角都是直角。
错误,能拼成一个平行四边形的两个三角形一定是完全一样的。(两个三角形可以完全重合)
在括号里填上合适的计量单位。
(1)北京至上海的高速铁路长约1318( )。
(2)足球场的面积约为7500( )。
(3)东北虎的体重可达320( )。
(4)小虹家的冰箱容积有240( )。
2
千米
平方米
千克
升
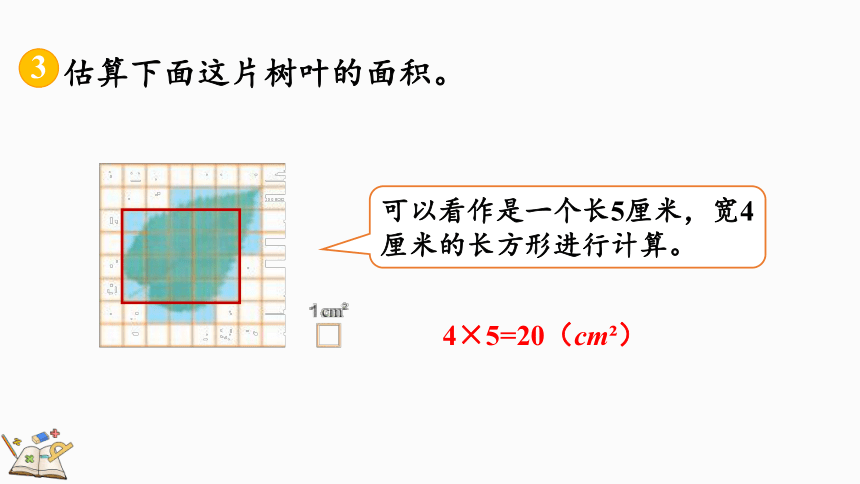
估算下面这片树叶的面积。
3
可以看作是一个长5厘米,宽4厘米的长方形进行计算。
4×5=20(cm )
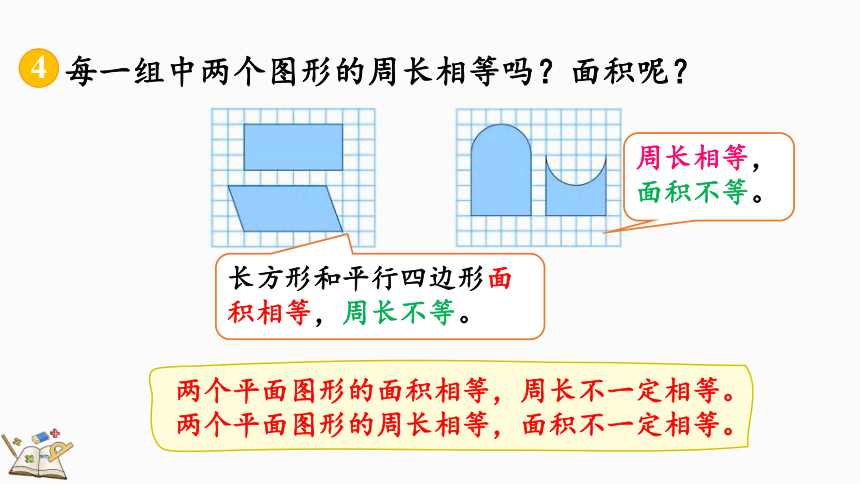
每一组中两个图形的周长相等吗?面积呢?
4
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
周长相等,
面积不等。
长方形和平行四边形面积相等,周长不等。
在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
5
平行四边形长是5,宽是2,面积为5×2=10
可以画长方形,三角形平行四边形,只要面积是10的图形即可。
一个平行四边形和一个三角形等底、等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
6
平行四边形面积=底×高=30cm
三角形面积=底×高÷2
30÷2=15(cm )
答:三角形的面积是15cm 。
30cm
你能画一条直线把下面每个图形分成面积相等的两部分吗?
每个图形你能找出多少种画法?你能发现什么?
7
可以画无数条
可以画无数条
可以画无数条
可以画无数条
发现:经过图中心的任意一条直线都能把图形分成相等的两部分。
下面这些图分别是从哪个方向看到的?
8
左面
上面
前面
把下面这个展开图折成一个长方体(字母在长方体的内侧)。
9
至少要量出3条不同长度的边的长度。例如,测量B面的长、宽及C面的宽。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么
哪一面在上面?
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
F面
E面
把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
10
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留一位小数。)
11
V =103=1000(cm3)
正方体
V = πr2h
圆锥
h=1000÷[ ((20÷2)2 ]
≈9.6(cm)
答:这个圆锥形铁块的高约是9.6cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。这堆纸箱可能有多少个 用学具试着摆一摆。
12
答:这堆纸箱可能有9或10个。
一个箱子下半部分的形状是棱长为20cm的正方体,上半部分的形状是圆柱的一半。算出它的表面积和体积。
13
20×20×5+3.14×(20÷2)2+3.14×20×20÷2
=2942(cm2)
20×20×20+3.14×(20÷2)2×20÷2
=11140(cm3)
答:它的表面积是2942cm2,体积是11140cm3。
右图是由棱长5cm的正方体搭成的几何体,所有表面都涂成了绿色。
14
(1)其中一共有多少个正方体 这个几何
体的体积是多少
(2)只有2个面涂色的正方体有多少个
(3)只有3个面涂色的正方体有多少个
(4)只有4个面涂色的正方体有多少个
(2)只有2个面涂色的正方体有2个。
(3)只有3个面涂色的正方体有2个。
(4)只有4个面涂色的正方体有6个。
5×5×5×10=1250(cm3)
答:一共有10个正方体,
它的体积是1250cm3。
一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
15
正方形的边长=扇形所在圆的半径
正方形的面积也就是半径的平方
3.14×10=31.4(cm2)
31.4×=7.85(cm2)
答:涂色部分的面积是7.85平方厘米。
用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多
16
用纸最多就是表面积最大
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24平方厘米。
24>22
1.把一个直径是6分米的圆剪成一个最大的正方形,这个正方形的面积是多少?
d=6dm
6×3÷2×2
答:正方形的面积是18平方分米。
=18÷2×2
=18(平方分米)
2.时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
答:分针走1小时,它的尖端走过的路程是113.04厘米。
3.
在长12.4厘米,宽7.2厘米的长方形纸中,剪半径是1厘米的圆,能剪多少个?画一画剪一剪。
方法一
方法二
可以剪18个
可以剪22个
4.
近年来,中国的建筑行业蓬勃发展,基建事业不断发展。2020年1月份新冠肺炎疫情爆发,医院床位紧张。1月23日,由中建三局牵头,指挥7500名建设者和近千台机械设备,承诺用十天时间建成一所可容纳1000张床位的救命医院——火神山医院。9天的时间,一座医院平地而起,第10天就开始启用,与疫情赛跑,与时间博弈,火神山医院的建立,是“中国速度”的又一个奇迹。在施工现场有一个圆锥形石子堆,底面周长为12.56米,高是18分米,用这些石子铺满一条长16米、宽3米的地面,能铺多厚?
18分米=1.8米
12.56÷3.14÷2=2(米)
3.14×2 ×1.8÷3÷16÷3=0.157(米)
答:能铺0.157米厚。
这节课有什么收获呢?
1.运用平面图形的周长面积的意义及计算
公式,灵活正确进行周长和面积计算。
2.利用体积公式,解决实际问题。
3.体会代数思想,发展创新思维。
从课时练中选取。
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
面积
体积
转化法
第14课时 练习十八
第六单元 整理和复面图形的周长和面积
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
平面图形的周长公式
a
b
a
.
r
d
C=2(a+b)
C=4a
C=2πr
C=πd
平面图形面积之间的关系
S=πr2
S=ab
S=ah
推导
转化
转化
推导
S=(a+b)h÷2
S=ah÷2
转化
S=a2
转化
推导
推导
立体图形体积之间的关系
推导
转化
转化
推导
V=abh
V=a3
V=sh
V= sh
推导
判断下面的说法是否正确,并说一说你的理由。
(1)大于90°的角就是钝角。
(2)两条直线相交构成的4个角中如果有一个角是直角,那
么其他3个角也是直角。
(3)任何两个等底、等高的三角形都能拼成一个平行四边形。
1
选自教材第88~90页练习十八
错误,钝角是大于90°而小于180°的角。
正确,互相垂直的两条线,形成的四个角都是直角。
错误,能拼成一个平行四边形的两个三角形一定是完全一样的。(两个三角形可以完全重合)
在括号里填上合适的计量单位。
(1)北京至上海的高速铁路长约1318( )。
(2)足球场的面积约为7500( )。
(3)东北虎的体重可达320( )。
(4)小虹家的冰箱容积有240( )。
2
千米
平方米
千克
升
估算下面这片树叶的面积。
3
可以看作是一个长5厘米,宽4厘米的长方形进行计算。
4×5=20(cm )
每一组中两个图形的周长相等吗?面积呢?
4
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
周长相等,
面积不等。
长方形和平行四边形面积相等,周长不等。
在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
5
平行四边形长是5,宽是2,面积为5×2=10
可以画长方形,三角形平行四边形,只要面积是10的图形即可。
一个平行四边形和一个三角形等底、等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
6
平行四边形面积=底×高=30cm
三角形面积=底×高÷2
30÷2=15(cm )
答:三角形的面积是15cm 。
30cm
你能画一条直线把下面每个图形分成面积相等的两部分吗?
每个图形你能找出多少种画法?你能发现什么?
7
可以画无数条
可以画无数条
可以画无数条
可以画无数条
发现:经过图中心的任意一条直线都能把图形分成相等的两部分。
下面这些图分别是从哪个方向看到的?
8
左面
上面
前面
把下面这个展开图折成一个长方体(字母在长方体的内侧)。
9
至少要量出3条不同长度的边的长度。例如,测量B面的长、宽及C面的宽。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么
哪一面在上面?
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
F面
E面
把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
10
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留一位小数。)
11
V =103=1000(cm3)
正方体
V = πr2h
圆锥
h=1000÷[ ((20÷2)2 ]
≈9.6(cm)
答:这个圆锥形铁块的高约是9.6cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。这堆纸箱可能有多少个 用学具试着摆一摆。
12
答:这堆纸箱可能有9或10个。
一个箱子下半部分的形状是棱长为20cm的正方体,上半部分的形状是圆柱的一半。算出它的表面积和体积。
13
20×20×5+3.14×(20÷2)2+3.14×20×20÷2
=2942(cm2)
20×20×20+3.14×(20÷2)2×20÷2
=11140(cm3)
答:它的表面积是2942cm2,体积是11140cm3。
右图是由棱长5cm的正方体搭成的几何体,所有表面都涂成了绿色。
14
(1)其中一共有多少个正方体 这个几何
体的体积是多少
(2)只有2个面涂色的正方体有多少个
(3)只有3个面涂色的正方体有多少个
(4)只有4个面涂色的正方体有多少个
(2)只有2个面涂色的正方体有2个。
(3)只有3个面涂色的正方体有2个。
(4)只有4个面涂色的正方体有6个。
5×5×5×10=1250(cm3)
答:一共有10个正方体,
它的体积是1250cm3。
一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
15
正方形的边长=扇形所在圆的半径
正方形的面积也就是半径的平方
3.14×10=31.4(cm2)
31.4×=7.85(cm2)
答:涂色部分的面积是7.85平方厘米。
用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多
16
用纸最多就是表面积最大
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24平方厘米。
24>22
1.把一个直径是6分米的圆剪成一个最大的正方形,这个正方形的面积是多少?
d=6dm
6×3÷2×2
答:正方形的面积是18平方分米。
=18÷2×2
=18(平方分米)
2.时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
答:分针走1小时,它的尖端走过的路程是113.04厘米。
3.
在长12.4厘米,宽7.2厘米的长方形纸中,剪半径是1厘米的圆,能剪多少个?画一画剪一剪。
方法一
方法二
可以剪18个
可以剪22个
4.
近年来,中国的建筑行业蓬勃发展,基建事业不断发展。2020年1月份新冠肺炎疫情爆发,医院床位紧张。1月23日,由中建三局牵头,指挥7500名建设者和近千台机械设备,承诺用十天时间建成一所可容纳1000张床位的救命医院——火神山医院。9天的时间,一座医院平地而起,第10天就开始启用,与疫情赛跑,与时间博弈,火神山医院的建立,是“中国速度”的又一个奇迹。在施工现场有一个圆锥形石子堆,底面周长为12.56米,高是18分米,用这些石子铺满一条长16米、宽3米的地面,能铺多厚?
18分米=1.8米
12.56÷3.14÷2=2(米)
3.14×2 ×1.8÷3÷16÷3=0.157(米)
答:能铺0.157米厚。
这节课有什么收获呢?
1.运用平面图形的周长面积的意义及计算
公式,灵活正确进行周长和面积计算。
2.利用体积公式,解决实际问题。
3.体会代数思想,发展创新思维。
从课时练中选取。
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
面积
体积
转化法
