6.2.4 图形的运动 课件(共17张PPT)人教版数学六年级下册
文档属性
| 名称 | 6.2.4 图形的运动 课件(共17张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第15课时 图形的运动
第六单元 整理和复习
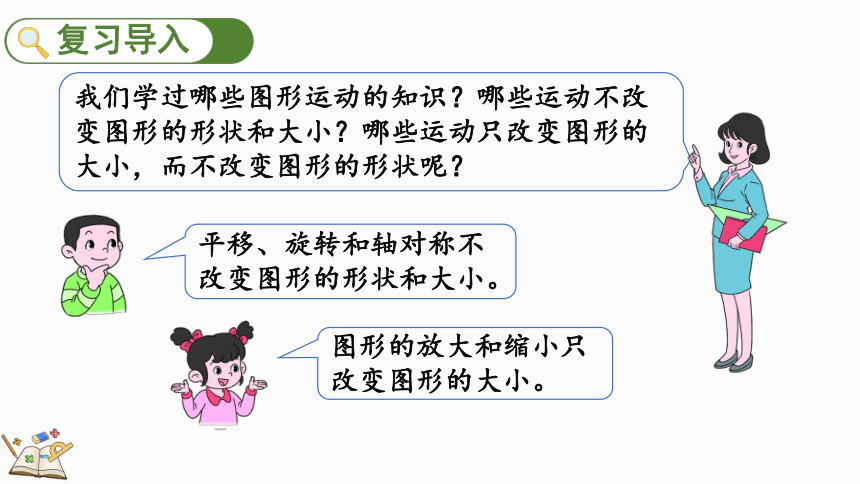
我们学过哪些图形运动的知识?哪些运动不改变图形的形状和大小?哪些运动只改变图形的大小,而不改变图形的形状呢?
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小。
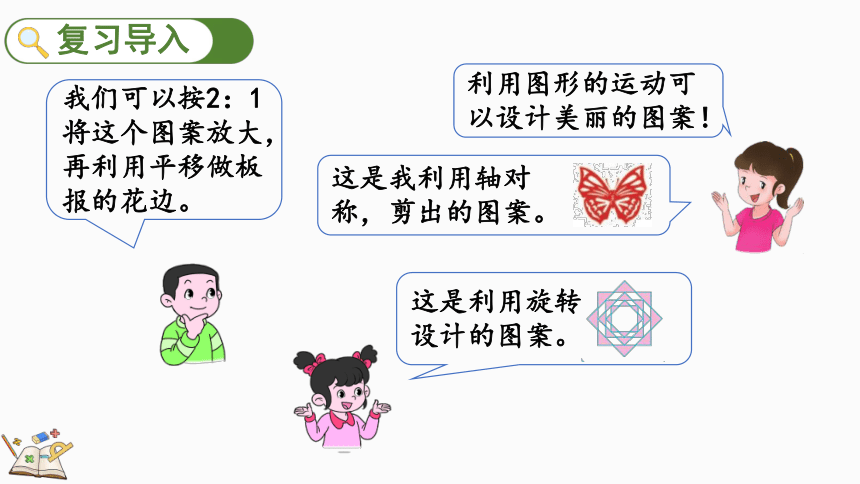
利用图形的运动可以设计美丽的图案!
我们可以按2:1将这个图案放大,再利用平移做板报的花边。
这是我利用轴对
称,剪出的图案。
这是利用旋转
设计的图案。
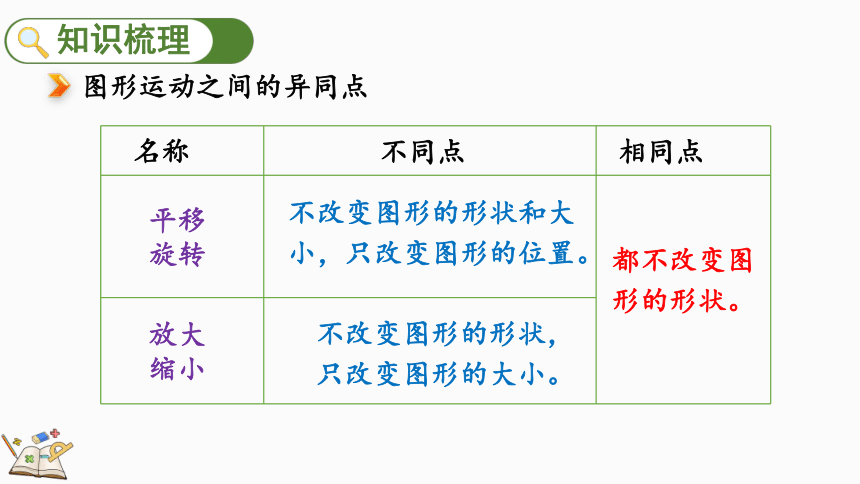
图形运动之间的异同点
名称
平移
旋转
放大
缩小
不同点
相同点
不改变图形的形状和大小,只改变图形的位置。
不改变图形的形状,只改变图形的大小。
都不改变图形的形状。
图形的平移
意 义
特 点
要 素
画 法
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是移动的方向,二是移动的距离。
要先确定方向,再确定平移的距离。
图形平移两个关键点:①平移的距离②平移的方向
图形的旋转
意 义
特 点
要 素
画 法
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
轴对称
意 义
特 点
画 法
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
图形的对称轴数量
图形 对称轴数量 图形 对称轴数量
线段 等腰梯形
角 圆
等腰三角形 环形
等边三角形 扇形
长方形 半圆
1条
3条
2条
4条
无数条
正方形
菱形
1条
1条
1条
无数条
1条
1条
2条
图形的放大与缩小
意 义
特 点
画 法
按一定比例,将一个图形放大或缩小,叫做图形的缩放。
图形的放大:比值大于1,如3∶1。
1.看比例,确定放大还是缩小。
2.算出放大或缩小后图形对应的边长。
3.画出图形。
图形的缩小:比值小于1,如1∶2。
选自教材第91页“做一做”。
图中A→B→C→D是怎样变化的?
1
A→B形状大小都没有发生变化,只是位置变了,所以是平移。
B→C形状大小都没有发生变化,只是角度变了,所以是旋转。
C→D形状大小都没有发生变化,只是角度变了,所以是旋转。
答:图A向右平移5格是B,再中心点绕逆时针旋转90°是C,然后再绕中心点逆时针旋转90°是D。
这些图案分别运用了哪种图形运动的知识?
2
根据本节知识点选自课外练习。
旋转45°
放大
平移
1.
在方格纸上画出图形B和图形C。
①图形A向下平移3个方格得到图形B。
②图形B绕O点顺时针旋转90度得到图形C。
O
A
O
B
C
O
A
2.
画出每个图形的另一半,使它成为轴对称图形。
3.
根据要求画一画。
1.把图①绕O点顺时针旋转90度。
2.把图②绕O点逆时针旋转90度。
①
②
4.
哪些图形是轴对称图形?
无数条
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
从课时练中选取。
平移 :方向 距离
旋转:中心点 方向 角度
放大和缩小:形状不变,大小改变
轴对称:对应点到对称轴的距离相等
第15课时 图形的运动
第六单元 整理和复习
我们学过哪些图形运动的知识?哪些运动不改变图形的形状和大小?哪些运动只改变图形的大小,而不改变图形的形状呢?
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小。
利用图形的运动可以设计美丽的图案!
我们可以按2:1将这个图案放大,再利用平移做板报的花边。
这是我利用轴对
称,剪出的图案。
这是利用旋转
设计的图案。
图形运动之间的异同点
名称
平移
旋转
放大
缩小
不同点
相同点
不改变图形的形状和大小,只改变图形的位置。
不改变图形的形状,只改变图形的大小。
都不改变图形的形状。
图形的平移
意 义
特 点
要 素
画 法
在同一平面内,将一个图形沿某个方向移动一定的距离,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是移动的方向,二是移动的距离。
要先确定方向,再确定平移的距离。
图形平移两个关键点:①平移的距离②平移的方向
图形的旋转
意 义
特 点
要 素
画 法
在平面内,一个图形绕一点沿一定方向转动一定角度,这样的运动叫图形的旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
轴对称
意 义
特 点
画 法
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
图形的对称轴数量
图形 对称轴数量 图形 对称轴数量
线段 等腰梯形
角 圆
等腰三角形 环形
等边三角形 扇形
长方形 半圆
1条
3条
2条
4条
无数条
正方形
菱形
1条
1条
1条
无数条
1条
1条
2条
图形的放大与缩小
意 义
特 点
画 法
按一定比例,将一个图形放大或缩小,叫做图形的缩放。
图形的放大:比值大于1,如3∶1。
1.看比例,确定放大还是缩小。
2.算出放大或缩小后图形对应的边长。
3.画出图形。
图形的缩小:比值小于1,如1∶2。
选自教材第91页“做一做”。
图中A→B→C→D是怎样变化的?
1
A→B形状大小都没有发生变化,只是位置变了,所以是平移。
B→C形状大小都没有发生变化,只是角度变了,所以是旋转。
C→D形状大小都没有发生变化,只是角度变了,所以是旋转。
答:图A向右平移5格是B,再中心点绕逆时针旋转90°是C,然后再绕中心点逆时针旋转90°是D。
这些图案分别运用了哪种图形运动的知识?
2
根据本节知识点选自课外练习。
旋转45°
放大
平移
1.
在方格纸上画出图形B和图形C。
①图形A向下平移3个方格得到图形B。
②图形B绕O点顺时针旋转90度得到图形C。
O
A
O
B
C
O
A
2.
画出每个图形的另一半,使它成为轴对称图形。
3.
根据要求画一画。
1.把图①绕O点顺时针旋转90度。
2.把图②绕O点逆时针旋转90度。
①
②
4.
哪些图形是轴对称图形?
无数条
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
从课时练中选取。
平移 :方向 距离
旋转:中心点 方向 角度
放大和缩小:形状不变,大小改变
轴对称:对应点到对称轴的距离相等
