6.4.1 找规律解决实际问题 课件(共19张PPT)人教版数学六年级下册
文档属性
| 名称 | 6.4.1 找规律解决实际问题 课件(共19张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 16:17:27 | ||
图片预览





文档简介
(共19张PPT)
第22课时 找规律解决实际问题
第六单元 整理和复习
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想方法。有的数或图形排列中存在着一定的规律,可以帮助我们解决问题。
找规律解决实际问题的步骤
01
观察发现
02
总结规律
03
解决问题
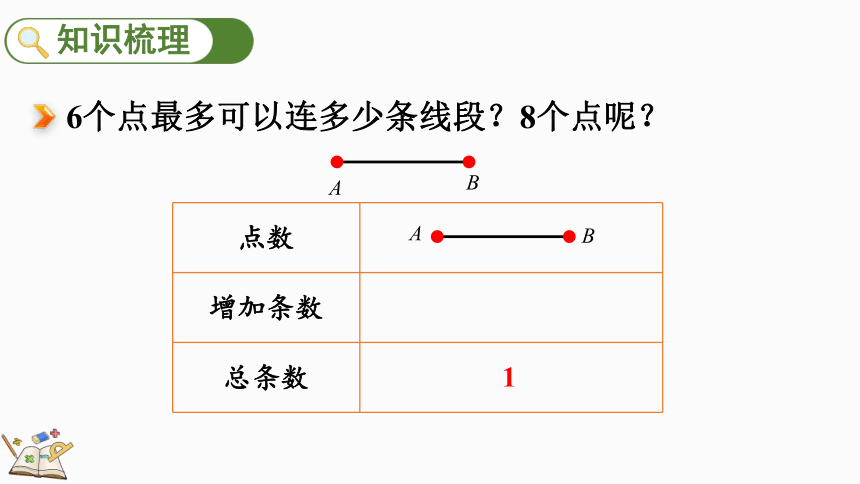
6个点最多可以连多少条线段?8个点呢?
太乱了,我都数晕了。
别着急,从2个点开始,逐渐增加点数,找找规律。
点数
增加条数
总条数
A
B
A
B
1
6个点最多可以连多少条线段?8个点呢?
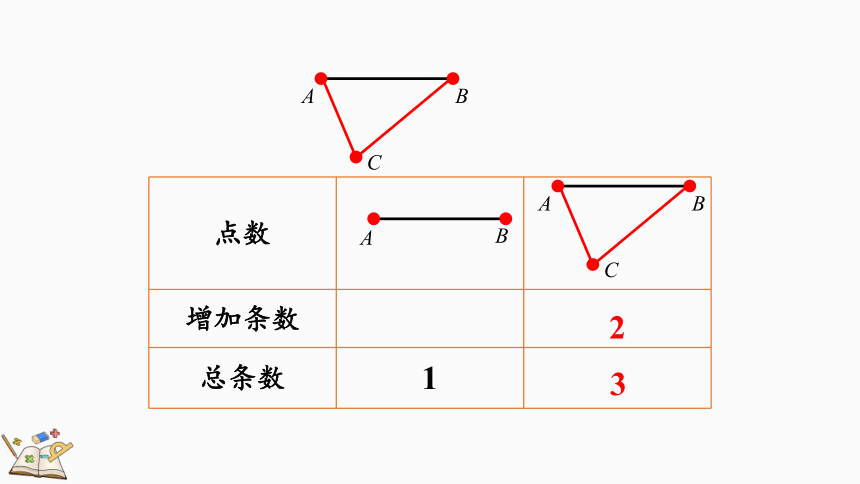
点数
增加条数
总条数 1
A
B
C
A
B
A
B
C
2
3
点数
增加条数 2
总条数 1 3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
A
B
C
D
E
点数
增加
条数 2 3
总条数 1 3 6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
点数 2个点 3个点 4个点 5个点 6个点
增加条数 2 3 4
总条数 1 3 6 10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
8个点共连:1+2+3+4+5+6+7=28(条)
6个点最多可以连多少条线段?8个点呢?
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
12个点共连:1+2+3+4+5+6+7+8+9+10+11=66(条)
根据规律,你知道12个点、20个点最多能连成多少条线段吗?请写出算式。
想一想:n个点最多能连多少条线段?
20个点共连:1+2+3+4+5+6+…+18+19=190(条)
n个点共连:1+2+3+ … +(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
选自教材第99页做一做
观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
①
②
③
④
1 4 9 16
7×7=49(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
15×15=225(个)
①
②
③
④
(2)*第n幅图有多少个棋子?
答:第n幅图有n 个棋子。
n×n=n
每行的棋子数×行数=棋子总数
1×1=1
2×2=4
3×3=9
4×4=16
选自教材第99页做一做
1.
“某软件”等级是用户资料和身份的象征,按照其中积分划分不同的等级.当用户在10级以上,每个等级与对应的积分有一定的关系.现在知道第10级的积分是90,第11级的积分是160,第12级的积分是250,第13级的积分是360,第14级的积分是490……若某用户的积分达到1000,则他的等级是( )。
17级
2.
观察下面一组算式,再填出适当的数。
(1) 1×9+2=11
(2) 12×9+3=111
(3) 123×9+4=1111
得数都是由数字1组成的;
第二个加数是几,得数就由几个1组成。
第一个加数是从1开始的自然数按照从小到大的顺序排列的,它的位数比后面的加数少1。
(4) 1234×9+5=( )
(5) 12345×9+( )=111111
(6) ( )×9+( )=11111111
11111
6
1234567
8
3.
根据下表中的排列规律,在空格里填上适当的数。
1 4
5 20
2 5
7 35
3 6
9 54
4
3
3
3
1+4=5
2+5=7
3+6=9
4+3=7
4+7=11
7×11=77
4×5=20
5×7=35
6×9=54
上面两个数的差是3
,下面第一个数是上面两个数的和。
下面第二个数是上面第二个数与下面第一个数的乘积。
7
11
77
4.
观察点阵图的规律,画出下一个图形。
后一个图比前一个图下方多一行,圆点多1,右边多一列,圆点数多1。
1
3
6
10
15
找一找规律,在括号里填上适当的数。
9,11,15,21,29,( ),( )。
(
+2
(
+4
(
+6
(
+8
39
51
1,2,3,1,2,6,1,2,12,( ),( ),( )。
3×2=6
6×2=12
1
2
12×2=24
24
(1)
(2)
29+10=39
39+12=51
(
+10
5.
1.从教材总复习中选取;
2.从课时练中选取。
找规律解决实际问题
观察发现
解决问题
总结规律
第22课时 找规律解决实际问题
第六单元 整理和复习
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想方法。有的数或图形排列中存在着一定的规律,可以帮助我们解决问题。
找规律解决实际问题的步骤
01
观察发现
02
总结规律
03
解决问题
6个点最多可以连多少条线段?8个点呢?
太乱了,我都数晕了。
别着急,从2个点开始,逐渐增加点数,找找规律。
点数
增加条数
总条数
A
B
A
B
1
6个点最多可以连多少条线段?8个点呢?
点数
增加条数
总条数 1
A
B
C
A
B
A
B
C
2
3
点数
增加条数 2
总条数 1 3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
A
B
C
D
E
点数
增加
条数 2 3
总条数 1 3 6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
点数 2个点 3个点 4个点 5个点 6个点
增加条数 2 3 4
总条数 1 3 6 10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
8个点共连:1+2+3+4+5+6+7=28(条)
6个点最多可以连多少条线段?8个点呢?
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
12个点共连:1+2+3+4+5+6+7+8+9+10+11=66(条)
根据规律,你知道12个点、20个点最多能连成多少条线段吗?请写出算式。
想一想:n个点最多能连多少条线段?
20个点共连:1+2+3+4+5+6+…+18+19=190(条)
n个点共连:1+2+3+ … +(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
选自教材第99页做一做
观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
①
②
③
④
1 4 9 16
7×7=49(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
15×15=225(个)
①
②
③
④
(2)*第n幅图有多少个棋子?
答:第n幅图有n 个棋子。
n×n=n
每行的棋子数×行数=棋子总数
1×1=1
2×2=4
3×3=9
4×4=16
选自教材第99页做一做
1.
“某软件”等级是用户资料和身份的象征,按照其中积分划分不同的等级.当用户在10级以上,每个等级与对应的积分有一定的关系.现在知道第10级的积分是90,第11级的积分是160,第12级的积分是250,第13级的积分是360,第14级的积分是490……若某用户的积分达到1000,则他的等级是( )。
17级
2.
观察下面一组算式,再填出适当的数。
(1) 1×9+2=11
(2) 12×9+3=111
(3) 123×9+4=1111
得数都是由数字1组成的;
第二个加数是几,得数就由几个1组成。
第一个加数是从1开始的自然数按照从小到大的顺序排列的,它的位数比后面的加数少1。
(4) 1234×9+5=( )
(5) 12345×9+( )=111111
(6) ( )×9+( )=11111111
11111
6
1234567
8
3.
根据下表中的排列规律,在空格里填上适当的数。
1 4
5 20
2 5
7 35
3 6
9 54
4
3
3
3
1+4=5
2+5=7
3+6=9
4+3=7
4+7=11
7×11=77
4×5=20
5×7=35
6×9=54
上面两个数的差是3
,下面第一个数是上面两个数的和。
下面第二个数是上面第二个数与下面第一个数的乘积。
7
11
77
4.
观察点阵图的规律,画出下一个图形。
后一个图比前一个图下方多一行,圆点多1,右边多一列,圆点数多1。
1
3
6
10
15
找一找规律,在括号里填上适当的数。
9,11,15,21,29,( ),( )。
(
+2
(
+4
(
+6
(
+8
39
51
1,2,3,1,2,6,1,2,12,( ),( ),( )。
3×2=6
6×2=12
1
2
12×2=24
24
(1)
(2)
29+10=39
39+12=51
(
+10
5.
1.从教材总复习中选取;
2.从课时练中选取。
找规律解决实际问题
观察发现
解决问题
总结规律
