6.4.2 列表法解决实际问题 课件(共17张PPT)人教版数学六年级下册
文档属性
| 名称 | 6.4.2 列表法解决实际问题 课件(共17张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 16:19:13 | ||
图片预览




文档简介
(共17张PPT)
第23课时 列表法解决实际问题
第六单元 整理和复习
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
有一些比较复杂的问题,用列表格的方法可以帮助我们分析解决。
1
2
列表法解决实际问题的步骤
3
表格罗列所有情况
分析排除矛盾情况
解决问题写出答案
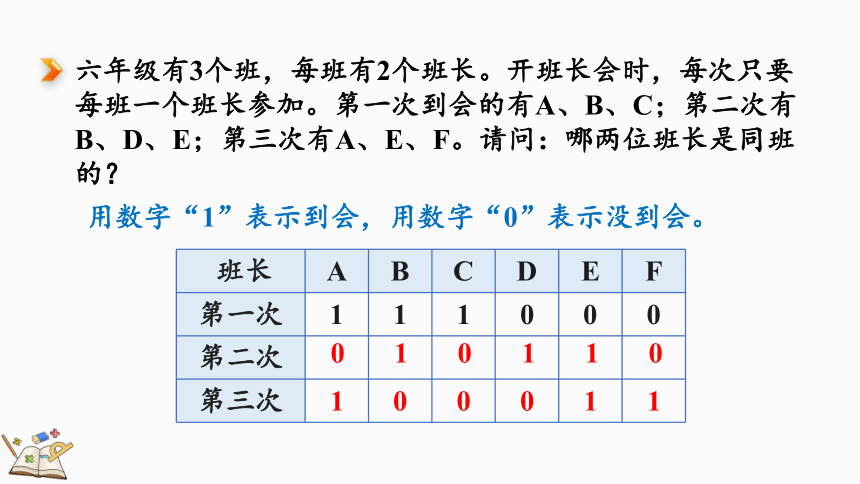
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
这个问题好复杂呀!
用列表的方法试一试!
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
用数字“1”表示到会,用数字“0”表示没到会。
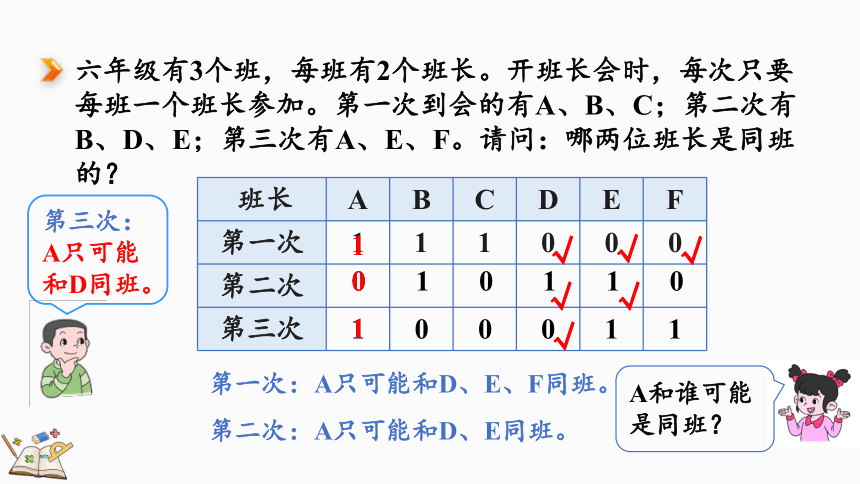
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
那一起参加班会的一定不在同一班级。
有且只有一个班长参加。
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
1
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
A和谁可能是同班?
第一次:A只可能和D、E、F同班。
第二次:A只可能和D、E同班。
第三次:A只可能和D同班。
1
√
√
√
√
√
0
1
√
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
B、C可能和谁是同班?
A和D同班,则B只可能和E、F同班,根据第二次推测,B和F同班,据此可推出C、E同班。
1
√
√
√
1
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
选自教材第100页做一做
王阿姨、刘阿姨、丁叔叔、李叔叔的职业分别是工人、教师、医生中的其中一种。王阿姨是教师,丁叔叔不是工人,只有刘阿姨和李叔叔的职业相同。
请问:他们的职业分别是什么
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
医生
√
×
×
√
×
×
√
√
答:王阿姨是教师,丁叔叔是医生,
刘阿姨和李叔叔是工人。
1.
球场休息时,保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了,结果甲喝的是丙的。乙、丙各喝的是谁的?
甲 乙 丙
甲的水
乙的水
丙的水
×
√
×
×
×
×
√
√
答:乙喝的是甲的,丙喝的是乙的。
×
2.
下图中一共有几条线段?
或7×(7-1)÷2=21(条)
(7-1)+5+4+3+2+1=21(条 )
答:一共有21条线段。
3.
“世界杯”是世界上知名度最高的足球比赛,与奥运会并称为全球体育两大最顶级赛事。2018年世界杯共有32支球队参加,平均分为8个小组,每小组内的每两支球队都要打一场比赛,组内积分最高的两支球队进入16强。要决出16强,这8个小组一共要打多少场比赛?
每个小组内打:3+2+1=6(场)
8个小组共打:6×8=48(场)
32÷8=4(支)
答:这8个小组一共要打48场。
4.
有红、黄、黑三种颜色的帽子。聪聪、明明、乐乐各戴了其中的一顶帽子。
聪聪说:“我戴的不是红色的。”
明明说:“我戴的也不是红色的。”
乐乐说:“聪聪戴的不是黑色的。”
你知道他们各戴了什么颜色的帽子吗
答:聪聪戴黄色的,明明戴黑色的,乐乐戴红色的。
说明乐乐戴的是红色。
聪聪戴的是黄色。
5.
为迎接国庆节,某街道打算在街道的一侧悬挂一些彩旗,每两蓝色旗之间插入5面红旗,如果有20面蓝色旗,那么需要准备多少面红旗
(20-1)×5=95(面)
答:需要准备95面红旗。
学校组织了足球,航模和电脑兴趣小组,小涛、圆圆和小勇分别参加了其中一项。圆圆不喜欢踢足球,小勇没有参加电脑小组,小涛喜欢航模。他们分别在哪个小组。
足球 航模 电脑
小涛
圆圆
小勇
×
×
×
×
×
×
√
√
√
答:小涛在航模小组,圆圆在电脑小组,
小勇在足球小组。
6.
1.从教材总复习中选取;
2.从课时练中选取。
列表法解决实际问题
表格罗列所有情况
分析排除矛盾情况
解决问题写出答案
第23课时 列表法解决实际问题
第六单元 整理和复习
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
有一些比较复杂的问题,用列表格的方法可以帮助我们分析解决。
1
2
列表法解决实际问题的步骤
3
表格罗列所有情况
分析排除矛盾情况
解决问题写出答案
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
这个问题好复杂呀!
用列表的方法试一试!
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
用数字“1”表示到会,用数字“0”表示没到会。
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
那一起参加班会的一定不在同一班级。
有且只有一个班长参加。
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
1
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
A和谁可能是同班?
第一次:A只可能和D、E、F同班。
第二次:A只可能和D、E同班。
第三次:A只可能和D同班。
1
√
√
√
√
√
0
1
√
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
班长 A B C D E F
第一次 1 1 1 0 0 0
第二次
第三次
0
1
0
1
1
0
1
0
0
0
1
1
B、C可能和谁是同班?
A和D同班,则B只可能和E、F同班,根据第二次推测,B和F同班,据此可推出C、E同班。
1
√
√
√
1
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
选自教材第100页做一做
王阿姨、刘阿姨、丁叔叔、李叔叔的职业分别是工人、教师、医生中的其中一种。王阿姨是教师,丁叔叔不是工人,只有刘阿姨和李叔叔的职业相同。
请问:他们的职业分别是什么
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
医生
√
×
×
√
×
×
√
√
答:王阿姨是教师,丁叔叔是医生,
刘阿姨和李叔叔是工人。
1.
球场休息时,保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了,结果甲喝的是丙的。乙、丙各喝的是谁的?
甲 乙 丙
甲的水
乙的水
丙的水
×
√
×
×
×
×
√
√
答:乙喝的是甲的,丙喝的是乙的。
×
2.
下图中一共有几条线段?
或7×(7-1)÷2=21(条)
(7-1)+5+4+3+2+1=21(条 )
答:一共有21条线段。
3.
“世界杯”是世界上知名度最高的足球比赛,与奥运会并称为全球体育两大最顶级赛事。2018年世界杯共有32支球队参加,平均分为8个小组,每小组内的每两支球队都要打一场比赛,组内积分最高的两支球队进入16强。要决出16强,这8个小组一共要打多少场比赛?
每个小组内打:3+2+1=6(场)
8个小组共打:6×8=48(场)
32÷8=4(支)
答:这8个小组一共要打48场。
4.
有红、黄、黑三种颜色的帽子。聪聪、明明、乐乐各戴了其中的一顶帽子。
聪聪说:“我戴的不是红色的。”
明明说:“我戴的也不是红色的。”
乐乐说:“聪聪戴的不是黑色的。”
你知道他们各戴了什么颜色的帽子吗
答:聪聪戴黄色的,明明戴黑色的,乐乐戴红色的。
说明乐乐戴的是红色。
聪聪戴的是黄色。
5.
为迎接国庆节,某街道打算在街道的一侧悬挂一些彩旗,每两蓝色旗之间插入5面红旗,如果有20面蓝色旗,那么需要准备多少面红旗
(20-1)×5=95(面)
答:需要准备95面红旗。
学校组织了足球,航模和电脑兴趣小组,小涛、圆圆和小勇分别参加了其中一项。圆圆不喜欢踢足球,小勇没有参加电脑小组,小涛喜欢航模。他们分别在哪个小组。
足球 航模 电脑
小涛
圆圆
小勇
×
×
×
×
×
×
√
√
√
答:小涛在航模小组,圆圆在电脑小组,
小勇在足球小组。
6.
1.从教材总复习中选取;
2.从课时练中选取。
列表法解决实际问题
表格罗列所有情况
分析排除矛盾情况
解决问题写出答案
